8.1.2 三角形的内角和与外角和 课件(共42张PPT)
文档属性
| 名称 | 8.1.2 三角形的内角和与外角和 课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览









文档简介
(共42张PPT)
8.1 与三角形有关的边和角
8.1.2 三角形的内角和与外角和
第8章 三角形
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.通过操作活动,使学生发现三角形的内角和是180°;
2.会利用三角形的内角和求三角形中未知角的度数;
3.掌握三角形的外角的性质及外角和.
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
将三角形纸片分别按下面两种方法进行折叠、剪拼等操作,你能发现什么?
折叠三角形纸板,可以把它的三个角拼成一个角.
可以将∠A,∠B 剪下并移至顶点C处拼接成一个角.
A
B
C
三角形的三个内角拼到一起恰好构成一个平角.
观察与思考
如图,已知△ABC,分别用∠1、∠2、∠3表示△ABC的三个内角,证明∠1+∠2+∠3=180°.
知识点1 三角形的内角和
观测的结果不一定可靠,还需要通过数学知识来说明.
C E
A
B
1
2
3
D
解:如图,延长边BC至点E,以点C为顶点,在BE的上侧作∠DCE=∠2,则CD//BA(同位角相等,两直线平行)
∵CD //BA,
∴∠1=∠ACD(两直线平行,内错角相等).
∵∠3+∠ACD+∠DCE=180°,
∴∠1+∠2+∠3=180°(等量代换).
由此得到:
你还能想出其它的方法推出这个结论吗?
三角形的内角和等于180°.
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
例1 在△ABC中,∠A的度数是∠B的度数的3倍,∠C比∠B大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,
∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
∴3x=99,x+15=48.
答: ∠A,∠B,∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
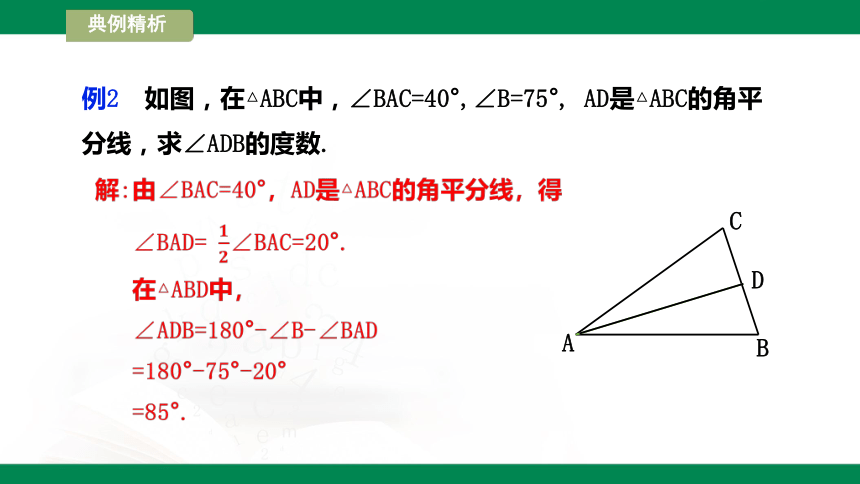
例2 如图,在△ABC中,∠BAC=40°,∠B=75°, AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40°,AD是△ABC的角平分线,得
∠BAD= ∠BAC=20°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
问题1 如图,在直角三角形ABC中,∠C=90°,∠A与∠B有什么关系?
A
B
C
知识点2 直角三角形的两锐角互余
由三角形的内角和等于180°,得
∠A+∠B+∠C=180°.
由此可以推出
∠A+∠B=180°∠C=90°,
即∠A与∠B互余.
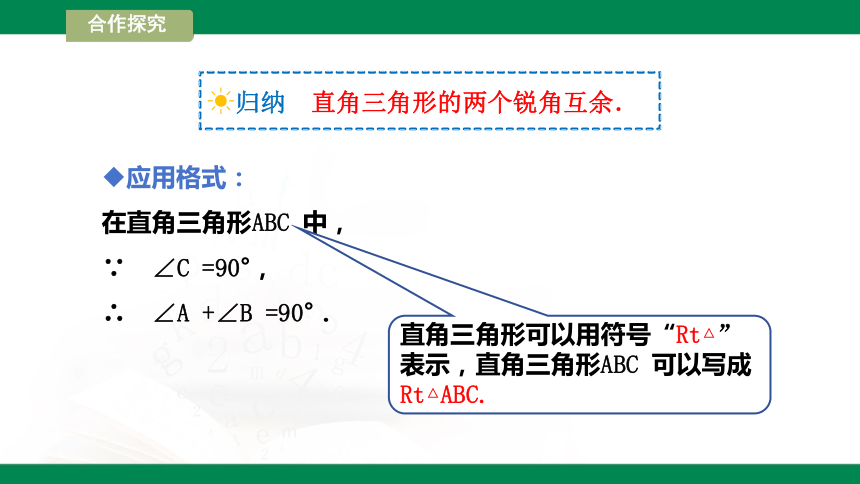
应用格式:
在直角三角形ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC.
归纳 直角三角形的两个锐角互余.
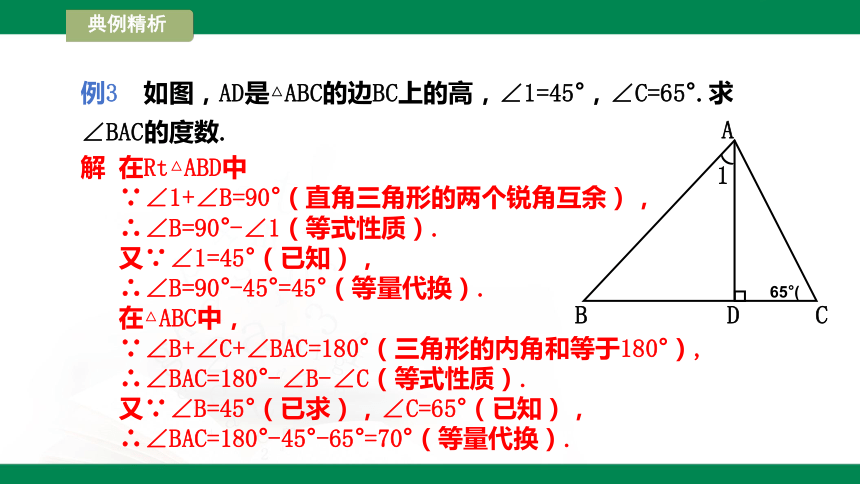
例3 如图,AD是△ABC的边BC上的高,∠1=45°,∠C=65°.求∠BAC的度数.
(
1
65°(
A
B D C
解 在Rt△ABD中
∵∠1+∠B=90°(直角三角形的两个锐角互余),
∴∠B=90°-∠1(等式性质).
又∵∠1=45°(已知),
∴∠B=90°-45°=45°(等量代换).
在△ABC中,
∵∠B+∠C+∠BAC=180°(三角形的内角和等于180°),
∴∠BAC=180°-∠B-∠C(等式性质).
又∵∠B=45°(已求),∠C=65°(已知),
∴∠BAC=180°-45°-65°=70°(等量代换).
我们已经知道,直角三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗?
由三角形的内角和等于180°,容易得出下面的结论:
有两个角互余的三角形是直角三角形.
问题1 如图,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.那么,外角∠ACD与它不相邻的内角∠A,∠B之间有什么大小关系?
我觉得可以利用“三角形的内角和等于180°”的结论.
知识点3 三角形的外角的性质
∵∠ACD+∠ACB = 180°,∠A +∠B +∠ACB = 180°,
∴∠ACD =180°-∠ACB,∠A +∠B =180°-∠ACB.
∴∠ACD =∠A +∠B.
由此可知,三角形的外角有两条性质:
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于任何一个与它不相邻的内角.
例4 如图,∠CAD=100°,∠B=30°,求∠C 的度数.
解:∵∠B+∠C=∠CAD,
∴∠C=∠CAD-∠B,
∴∠C=100°-30°=70°.
A
B
C
(
(
(
(
(
(
2
1
3
(
4
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角,如∠1和∠4.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图所示,∠1+∠2+∠3
就是△ABC的外角和.
问题2 如图,∠1、∠2、∠3是△ABC的三个外角,它们的和是多少?
解:在图中,有
∠1+∠ACB=180°,∠2+∠BAC=180°,
∠3+∠ABC=180°,
三式相加,可以得到
∠1+∠2+∠3+∠ACB+∠BAC+∠ABC=360°,
而∠ACB+∠BAC+∠ABC=180°,
∴∠1+ ∠2+ ∠3=360 °.
A
B
C
(
(
(
(
(
(
2
1
3
由此可知,三角形的外角和等于360°.
∠1+ ∠2+ ∠3=360 °.
A
B
C
(
(
(
(
(
(
2
1
3
A
B D C
例5 如图,D是△ABC的边BC上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
(1)求∠B的度数;
(2)求∠C的度数.
解 (1)∵∠ADC是△ABD的外角(已知),
∴∠B+∠BAD=∠ADC=80°(三角形的一个外角等
于与它不相邻的两个内角的和).
又∵∠B=∠BAD(已知),
∠B=80°×=40°(等量代换).
A
B D C
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和等于180°),
∴∠C=180°-∠B-∠BAC(等式的性质).
又∵∠B=40°(已求),∠BAC=70°(已知),
∴∠C=180°-40°-70°=70°(等量代换).
规律总结 在三角形中求角的度数时,常用的知识点有三个:(1)三角形的内角和等于180°;(2)三角形的一个外角等于与它不相邻的两个内角的和;(3)三角形的每一个内角与它相邻的外角互补.
1.已知△ABC中,∠A=70°,∠C=30°,∠B=______.
2.直角三角形一个锐角为70°,另一个锐角是_______.
3.在△ABC中,∠A=80°,∠B=∠C,则∠C=_______.
80°
20°
50°
4.如图,AD是△ABC的角平分线,∠B= 36°,∠C= 76°,则∠DAC的度数为________.
34°
1. 如图,已知是的 边延长线上一
点,且满足 , ,则 的度数为
( )
B
(第1题)
A. B. C. D.
返回
(第2题)
2. 如图,,为 的两个
外角, , ,
则 的邻补角是( )
C
A. B. C. D.
返回
3. 如图,,, 的大小关系是( )
B
(第3题)
A. B.
C. D.
无法确定三个角存在的外角与内角的关系导致判断
错误.
返回
(第4题)
4. 一天,李明和爸爸一起到建筑工地去,
看见了一个如图所示的人字架,爸爸说:
“李明,我考考你,若这个人字架中的
,你能求出比 大多少
吗?”请你帮李明计算一下,正确的答案
是( )
C
A. B. C. D.
返回
(第5题)
5. [2024北京朝阳区期中] 一副三角板按
如图所示摆放,其中,图中 的
度数为( )
C
A. B. C. D.
返回
(第6题)
6.[2024柳州期中] 如图,在 中,
,分别是,上的点,点在
的延长线上,, ,
,则 ______.
返回
7.如图,已知 , ,且
.若 ,求 的度数.
【解】延长交于点 ,如图.
, ,
.
.
,是 的外角,
.
返回
(第8题)
8. [2024郑州期末] 如图,在
中,,为边 上的动点
(不与点,重合),点在边 上,
始终保持.当 的度
数每增加 时, 的度数( )
C
A. 增加 B. 减小 C. 增加 D. 减小
(第8题)
【点拨】
,
, ,
.
又, .
当的度数每增加 时,
的度数增加 .
返回
(第9题)
9. 如图,已知 ,
,是上的一点,连结 ,
将沿所在直线折叠,点 落在
点处,连结,.若 ,
,则
( )
D
A. B. C. D.
【点拨】如图,延长交 于点
, .由折叠的性
质可知 .
. ,
.又, ,
.
.
,
.
. .
. .
故选D.
返回
(第10题)
10. 如图是可调躺椅示意图,
与的交点为, ,
, .为了舒适,需调
整大小,使 ,且
,,保持不变,则图中 应
调整为____ .
50
【点拨】如图,延长交于点 ,
, ,
.
.
, ,
.
又 , , ,
即应调整为 .
返回
(第11题)
11.如图,是中 的平分线,
是的外角 的平分线,如果
, ,则
____.
(第11题)
【点拨】是中 的平分线,
是的外角 的平分线,
, ,
,
.
,
.
内角和
三角形的内角和与外角和
三角形内角和等于180°
直角三角形两锐角互余
外角
1.外角的性质
2.三角形的外角和
谢谢观看!
8.1 与三角形有关的边和角
8.1.2 三角形的内角和与外角和
第8章 三角形
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.通过操作活动,使学生发现三角形的内角和是180°;
2.会利用三角形的内角和求三角形中未知角的度数;
3.掌握三角形的外角的性质及外角和.
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
将三角形纸片分别按下面两种方法进行折叠、剪拼等操作,你能发现什么?
折叠三角形纸板,可以把它的三个角拼成一个角.
可以将∠A,∠B 剪下并移至顶点C处拼接成一个角.
A
B
C
三角形的三个内角拼到一起恰好构成一个平角.
观察与思考
如图,已知△ABC,分别用∠1、∠2、∠3表示△ABC的三个内角,证明∠1+∠2+∠3=180°.
知识点1 三角形的内角和
观测的结果不一定可靠,还需要通过数学知识来说明.
C E
A
B
1
2
3
D
解:如图,延长边BC至点E,以点C为顶点,在BE的上侧作∠DCE=∠2,则CD//BA(同位角相等,两直线平行)
∵CD //BA,
∴∠1=∠ACD(两直线平行,内错角相等).
∵∠3+∠ACD+∠DCE=180°,
∴∠1+∠2+∠3=180°(等量代换).
由此得到:
你还能想出其它的方法推出这个结论吗?
三角形的内角和等于180°.
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
例1 在△ABC中,∠A的度数是∠B的度数的3倍,∠C比∠B大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,
∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
∴3x=99,x+15=48.
答: ∠A,∠B,∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
例2 如图,在△ABC中,∠BAC=40°,∠B=75°, AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40°,AD是△ABC的角平分线,得
∠BAD= ∠BAC=20°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
问题1 如图,在直角三角形ABC中,∠C=90°,∠A与∠B有什么关系?
A
B
C
知识点2 直角三角形的两锐角互余
由三角形的内角和等于180°,得
∠A+∠B+∠C=180°.
由此可以推出
∠A+∠B=180°∠C=90°,
即∠A与∠B互余.
应用格式:
在直角三角形ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC.
归纳 直角三角形的两个锐角互余.
例3 如图,AD是△ABC的边BC上的高,∠1=45°,∠C=65°.求∠BAC的度数.
(
1
65°(
A
B D C
解 在Rt△ABD中
∵∠1+∠B=90°(直角三角形的两个锐角互余),
∴∠B=90°-∠1(等式性质).
又∵∠1=45°(已知),
∴∠B=90°-45°=45°(等量代换).
在△ABC中,
∵∠B+∠C+∠BAC=180°(三角形的内角和等于180°),
∴∠BAC=180°-∠B-∠C(等式性质).
又∵∠B=45°(已求),∠C=65°(已知),
∴∠BAC=180°-45°-65°=70°(等量代换).
我们已经知道,直角三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗?
由三角形的内角和等于180°,容易得出下面的结论:
有两个角互余的三角形是直角三角形.
问题1 如图,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.那么,外角∠ACD与它不相邻的内角∠A,∠B之间有什么大小关系?
我觉得可以利用“三角形的内角和等于180°”的结论.
知识点3 三角形的外角的性质
∵∠ACD+∠ACB = 180°,∠A +∠B +∠ACB = 180°,
∴∠ACD =180°-∠ACB,∠A +∠B =180°-∠ACB.
∴∠ACD =∠A +∠B.
由此可知,三角形的外角有两条性质:
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于任何一个与它不相邻的内角.
例4 如图,∠CAD=100°,∠B=30°,求∠C 的度数.
解:∵∠B+∠C=∠CAD,
∴∠C=∠CAD-∠B,
∴∠C=100°-30°=70°.
A
B
C
(
(
(
(
(
(
2
1
3
(
4
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角,如∠1和∠4.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图所示,∠1+∠2+∠3
就是△ABC的外角和.
问题2 如图,∠1、∠2、∠3是△ABC的三个外角,它们的和是多少?
解:在图中,有
∠1+∠ACB=180°,∠2+∠BAC=180°,
∠3+∠ABC=180°,
三式相加,可以得到
∠1+∠2+∠3+∠ACB+∠BAC+∠ABC=360°,
而∠ACB+∠BAC+∠ABC=180°,
∴∠1+ ∠2+ ∠3=360 °.
A
B
C
(
(
(
(
(
(
2
1
3
由此可知,三角形的外角和等于360°.
∠1+ ∠2+ ∠3=360 °.
A
B
C
(
(
(
(
(
(
2
1
3
A
B D C
例5 如图,D是△ABC的边BC上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
(1)求∠B的度数;
(2)求∠C的度数.
解 (1)∵∠ADC是△ABD的外角(已知),
∴∠B+∠BAD=∠ADC=80°(三角形的一个外角等
于与它不相邻的两个内角的和).
又∵∠B=∠BAD(已知),
∠B=80°×=40°(等量代换).
A
B D C
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和等于180°),
∴∠C=180°-∠B-∠BAC(等式的性质).
又∵∠B=40°(已求),∠BAC=70°(已知),
∴∠C=180°-40°-70°=70°(等量代换).
规律总结 在三角形中求角的度数时,常用的知识点有三个:(1)三角形的内角和等于180°;(2)三角形的一个外角等于与它不相邻的两个内角的和;(3)三角形的每一个内角与它相邻的外角互补.
1.已知△ABC中,∠A=70°,∠C=30°,∠B=______.
2.直角三角形一个锐角为70°,另一个锐角是_______.
3.在△ABC中,∠A=80°,∠B=∠C,则∠C=_______.
80°
20°
50°
4.如图,AD是△ABC的角平分线,∠B= 36°,∠C= 76°,则∠DAC的度数为________.
34°
1. 如图,已知是的 边延长线上一
点,且满足 , ,则 的度数为
( )
B
(第1题)
A. B. C. D.
返回
(第2题)
2. 如图,,为 的两个
外角, , ,
则 的邻补角是( )
C
A. B. C. D.
返回
3. 如图,,, 的大小关系是( )
B
(第3题)
A. B.
C. D.
无法确定三个角存在的外角与内角的关系导致判断
错误.
返回
(第4题)
4. 一天,李明和爸爸一起到建筑工地去,
看见了一个如图所示的人字架,爸爸说:
“李明,我考考你,若这个人字架中的
,你能求出比 大多少
吗?”请你帮李明计算一下,正确的答案
是( )
C
A. B. C. D.
返回
(第5题)
5. [2024北京朝阳区期中] 一副三角板按
如图所示摆放,其中,图中 的
度数为( )
C
A. B. C. D.
返回
(第6题)
6.[2024柳州期中] 如图,在 中,
,分别是,上的点,点在
的延长线上,, ,
,则 ______.
返回
7.如图,已知 , ,且
.若 ,求 的度数.
【解】延长交于点 ,如图.
, ,
.
.
,是 的外角,
.
返回
(第8题)
8. [2024郑州期末] 如图,在
中,,为边 上的动点
(不与点,重合),点在边 上,
始终保持.当 的度
数每增加 时, 的度数( )
C
A. 增加 B. 减小 C. 增加 D. 减小
(第8题)
【点拨】
,
, ,
.
又, .
当的度数每增加 时,
的度数增加 .
返回
(第9题)
9. 如图,已知 ,
,是上的一点,连结 ,
将沿所在直线折叠,点 落在
点处,连结,.若 ,
,则
( )
D
A. B. C. D.
【点拨】如图,延长交 于点
, .由折叠的性
质可知 .
. ,
.又, ,
.
.
,
.
. .
. .
故选D.
返回
(第10题)
10. 如图是可调躺椅示意图,
与的交点为, ,
, .为了舒适,需调
整大小,使 ,且
,,保持不变,则图中 应
调整为____ .
50
【点拨】如图,延长交于点 ,
, ,
.
.
, ,
.
又 , , ,
即应调整为 .
返回
(第11题)
11.如图,是中 的平分线,
是的外角 的平分线,如果
, ,则
____.
(第11题)
【点拨】是中 的平分线,
是的外角 的平分线,
, ,
,
.
,
.
内角和
三角形的内角和与外角和
三角形内角和等于180°
直角三角形两锐角互余
外角
1.外角的性质
2.三角形的外角和
谢谢观看!
