第6章 一次方程组章末复习 课件(共35张PPT)
文档属性
| 名称 | 第6章 一次方程组章末复习 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 22:06:40 | ||
图片预览











文档简介
(共35张PPT)
章末复习
第6章 一次方程组
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
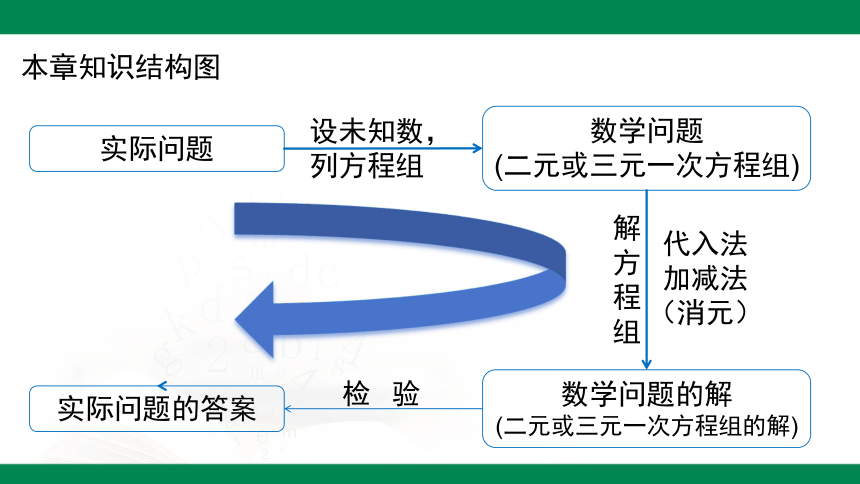
本章知识结构图
实际问题
实际问题的答案
数学问题
(二元或三元一次方程组)
数学问题的解
(二元或三元一次方程组的解)
设未知数,列方程组
检 验
解方程组
代入法
加减法(消元)
一、方程(组)的有关概念
1.二元一次方程的概念:有______未知数,并且含有未知数的项的次数都是_____的方程,叫做二元一次方程.
2.二元一次方程组的概念:两个_____ _方程合在一起,就组成了一个二元一次方程组.
两个
1
二元一次
要点梳理
一、方程(组)的有关概念
3.二元一次方程组的解:使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
4.三元一次方程组的概念:由三个_____方程组成的含有_______未知数的方程组叫做三元一次方程组.
一次
三个
要点梳理
二、二元一次方程组的解法
(1)代入法:从一个方程中求出某一个未知数的表达式,再把它“代入”另一个方程,进行求解,这种方法叫做代入消元法,简称代入法.
(2)加减法:把方程的两边分别相加或相减消去一个未知数的方法,叫做加减消元法,简称加减法.
三、三元一次方程组的解法
消元法:通过消元,把一个较复杂的三元一次方程组转化为简单易解的阶梯形的方程组,从而通过回代得出其解,整个求解过程称为用消元法解三元一次方程组.
1.列方程组的应用题的一般步骤:
审:审清题意,分清题中的已知量、未知量.
设:设未知数.
列:根据题意寻找等量关系列方程.
解:解方程(组).
验:检验方程的解是否符合题意.
答:写出答案(包括单位).
[注意] 审题是基础,找等量关系是关键.
四、用一次方程组解决实际问题
2.常见的几种方程类型及等量关系:
(1)行程问题中基本量之间的关系:
① 路程=速度×时间;
②相遇问题:全路程=甲走的路程+乙走的路程;
③追及问题:甲为快者,被追路程=甲走路程-乙走路程;
④流水问题:v顺=v静+v水,v逆=v静-v水.
(2)等积变形问题中基本量之间的关系:
① 原料面积=成品面积;
② 原料体积=成品体积.
(4)销售问题中基本量之间的关系:
① 实际售价-进价(成本)=利润;
② 利润÷进价×100%=利润率;
③ 进价×(1+利润率)=售价;标价×折扣数÷10=进价.
(3)储蓄问题中基本量之间的关系:
① 本金×利率×年数=利息;
② 本金+利息=本息和.
考点1 二元一次方程(组)的解
1. [2024青岛期中] 如果是方程组 的解,
则 的值为( )
C
A. 1 B. 2 C. 3 D. 4
返回
2.[2024泸州月考] 已知与都是关于, 的方
程 的解.
(1)求, 的值;
【解】与都是关于,的方程
的解,解得
(2)若也是方程的解,求 的值.
【解】当,时,原方程为 .
也是方程 的解,
,解得 .
返回
考点2 解二元一次方程组
3. 解下列方程组:
(1)[2024苏州]
【解】得,即 .
将代入①得,解得 .
所以原方程组的解为
(2)
【解】原方程组整理得
得 ,③
得,解得 .
把代入②得,解得 ,
所以原方程组的解为
(3)
【解】由得 ,④
把④代入③得,解得 .
把代入①②得解得
所以方程组的解为
返回
4.已知 是一个方程组.圆圆说:“这个方程
组的解是而我由于看错了第二个方程中 的系数,求
出的解是 ”请你根据以上信息,把方程组复
原出来.
【解】设为,●为, 为, 这个方程组的解是
看错了第二个方程中
的系数,求出的解是
解得所以原方程组为
返回
考点3 二元一次方程组的应用
5. [2024海南期中] 已知单项式与 是同类
项,那么, 的值分别是( )
C
A. 2, B. , C. 2,1 D. ,1
【点拨】 单项式与 是同类项,
把代入,得 ,
解得 .
把代入,解得 .
返回
6. 化学方程式是用化学式来表示物质化学反应
的式子.化学方程式不仅表明了反应物、生成物和反应条件,
同时化学计量数代表了各反应物、生成物物质的量关系,例
如就表示两份(氢气)与一份 (氧气)
点燃生成两份 (水).依据化学反应过程中的质量守恒定
律,在化学方程式等号左边和等号右边同一元素原子的个数
一定相同.已知 ,由此可列
出关于, 的二元一次方程为( )
D
A. B.
C. D.
返回
7.[2024吉林模拟] 扎染文化是我国传统文化的重要组成部分,
扎染文化的发展带动了旅游相关产业的发展.云南大理某扎染
坊第一次用3 700元购进甲种布料25件,乙种布料55件;第
二次以同样的价格用3 800元购进甲种布料50件,乙种布料
20件.该扎染坊购进的甲、乙两种布料的单价各是多少元?
【解】设该扎染坊购进的甲种布料的单价为 元,乙种布料
的单价为 元,
由题意得解得
答:该扎染坊购进的甲种布料的单价是60元,乙种布料的单
价是40元.
返回
8.甲、乙两人在某环形道路上跑步,假设他们在跑步过程中
各自保持一定的速度不变.如果他们同时从同一地点反向而行,
那么就会形成每隔10分钟相遇一次的规律;如果他们同时从
同一地点同向而行,那么5分钟后甲在乙的前方200米处,并
且他们的相遇规律变成了每隔100分钟相遇一次.求甲的速度
和环形道路的长度.
【解】设甲的速度为米/分,乙的速度为 米/分,环形道路
的长度为 米,
依题意得解得
答:甲的速度为220米/分,环形道路的长度为4 000米.
返回
思想1 转化思想
9.已知,,, ,中每个数只能取 ,0,2中
的一个,且满足
则 _____.
627
【点拨】设有个数取, 个数取2,
则解得
.
返回
思想2 整体思想
10.[2024郑州月考] 在数学课上,老师教给了同学们一种新的
解方程组的方法,例如:解方程组 时,
可由①得,③ 然后将③代入②,得 ,
解得,从而进一步得 这种方法被称为“整体
代入法”.
(1)用上述方法解方程组
【解】
由①,得 ,③
把③代入②,得,解得 .
将代入③,得,解得 .
方程组的解为
(2)若方程组的解是 求方程组
的解.
方程组的解是
在方程组中 解得
返回
谢谢观看!
章末复习
第6章 一次方程组
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
本章知识结构图
实际问题
实际问题的答案
数学问题
(二元或三元一次方程组)
数学问题的解
(二元或三元一次方程组的解)
设未知数,列方程组
检 验
解方程组
代入法
加减法(消元)
一、方程(组)的有关概念
1.二元一次方程的概念:有______未知数,并且含有未知数的项的次数都是_____的方程,叫做二元一次方程.
2.二元一次方程组的概念:两个_____ _方程合在一起,就组成了一个二元一次方程组.
两个
1
二元一次
要点梳理
一、方程(组)的有关概念
3.二元一次方程组的解:使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
4.三元一次方程组的概念:由三个_____方程组成的含有_______未知数的方程组叫做三元一次方程组.
一次
三个
要点梳理
二、二元一次方程组的解法
(1)代入法:从一个方程中求出某一个未知数的表达式,再把它“代入”另一个方程,进行求解,这种方法叫做代入消元法,简称代入法.
(2)加减法:把方程的两边分别相加或相减消去一个未知数的方法,叫做加减消元法,简称加减法.
三、三元一次方程组的解法
消元法:通过消元,把一个较复杂的三元一次方程组转化为简单易解的阶梯形的方程组,从而通过回代得出其解,整个求解过程称为用消元法解三元一次方程组.
1.列方程组的应用题的一般步骤:
审:审清题意,分清题中的已知量、未知量.
设:设未知数.
列:根据题意寻找等量关系列方程.
解:解方程(组).
验:检验方程的解是否符合题意.
答:写出答案(包括单位).
[注意] 审题是基础,找等量关系是关键.
四、用一次方程组解决实际问题
2.常见的几种方程类型及等量关系:
(1)行程问题中基本量之间的关系:
① 路程=速度×时间;
②相遇问题:全路程=甲走的路程+乙走的路程;
③追及问题:甲为快者,被追路程=甲走路程-乙走路程;
④流水问题:v顺=v静+v水,v逆=v静-v水.
(2)等积变形问题中基本量之间的关系:
① 原料面积=成品面积;
② 原料体积=成品体积.
(4)销售问题中基本量之间的关系:
① 实际售价-进价(成本)=利润;
② 利润÷进价×100%=利润率;
③ 进价×(1+利润率)=售价;标价×折扣数÷10=进价.
(3)储蓄问题中基本量之间的关系:
① 本金×利率×年数=利息;
② 本金+利息=本息和.
考点1 二元一次方程(组)的解
1. [2024青岛期中] 如果是方程组 的解,
则 的值为( )
C
A. 1 B. 2 C. 3 D. 4
返回
2.[2024泸州月考] 已知与都是关于, 的方
程 的解.
(1)求, 的值;
【解】与都是关于,的方程
的解,解得
(2)若也是方程的解,求 的值.
【解】当,时,原方程为 .
也是方程 的解,
,解得 .
返回
考点2 解二元一次方程组
3. 解下列方程组:
(1)[2024苏州]
【解】得,即 .
将代入①得,解得 .
所以原方程组的解为
(2)
【解】原方程组整理得
得 ,③
得,解得 .
把代入②得,解得 ,
所以原方程组的解为
(3)
【解】由得 ,④
把④代入③得,解得 .
把代入①②得解得
所以方程组的解为
返回
4.已知 是一个方程组.圆圆说:“这个方程
组的解是而我由于看错了第二个方程中 的系数,求
出的解是 ”请你根据以上信息,把方程组复
原出来.
【解】设为,●为, 为, 这个方程组的解是
看错了第二个方程中
的系数,求出的解是
解得所以原方程组为
返回
考点3 二元一次方程组的应用
5. [2024海南期中] 已知单项式与 是同类
项,那么, 的值分别是( )
C
A. 2, B. , C. 2,1 D. ,1
【点拨】 单项式与 是同类项,
把代入,得 ,
解得 .
把代入,解得 .
返回
6. 化学方程式是用化学式来表示物质化学反应
的式子.化学方程式不仅表明了反应物、生成物和反应条件,
同时化学计量数代表了各反应物、生成物物质的量关系,例
如就表示两份(氢气)与一份 (氧气)
点燃生成两份 (水).依据化学反应过程中的质量守恒定
律,在化学方程式等号左边和等号右边同一元素原子的个数
一定相同.已知 ,由此可列
出关于, 的二元一次方程为( )
D
A. B.
C. D.
返回
7.[2024吉林模拟] 扎染文化是我国传统文化的重要组成部分,
扎染文化的发展带动了旅游相关产业的发展.云南大理某扎染
坊第一次用3 700元购进甲种布料25件,乙种布料55件;第
二次以同样的价格用3 800元购进甲种布料50件,乙种布料
20件.该扎染坊购进的甲、乙两种布料的单价各是多少元?
【解】设该扎染坊购进的甲种布料的单价为 元,乙种布料
的单价为 元,
由题意得解得
答:该扎染坊购进的甲种布料的单价是60元,乙种布料的单
价是40元.
返回
8.甲、乙两人在某环形道路上跑步,假设他们在跑步过程中
各自保持一定的速度不变.如果他们同时从同一地点反向而行,
那么就会形成每隔10分钟相遇一次的规律;如果他们同时从
同一地点同向而行,那么5分钟后甲在乙的前方200米处,并
且他们的相遇规律变成了每隔100分钟相遇一次.求甲的速度
和环形道路的长度.
【解】设甲的速度为米/分,乙的速度为 米/分,环形道路
的长度为 米,
依题意得解得
答:甲的速度为220米/分,环形道路的长度为4 000米.
返回
思想1 转化思想
9.已知,,, ,中每个数只能取 ,0,2中
的一个,且满足
则 _____.
627
【点拨】设有个数取, 个数取2,
则解得
.
返回
思想2 整体思想
10.[2024郑州月考] 在数学课上,老师教给了同学们一种新的
解方程组的方法,例如:解方程组 时,
可由①得,③ 然后将③代入②,得 ,
解得,从而进一步得 这种方法被称为“整体
代入法”.
(1)用上述方法解方程组
【解】
由①,得 ,③
把③代入②,得,解得 .
将代入③,得,解得 .
方程组的解为
(2)若方程组的解是 求方程组
的解.
方程组的解是
在方程组中 解得
返回
谢谢观看!
