第7章 一元一次不等式 章末复习课件(共44张PPT)
文档属性
| 名称 | 第7章 一元一次不等式 章末复习课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
章末复习
第7章 一元一次不等式
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
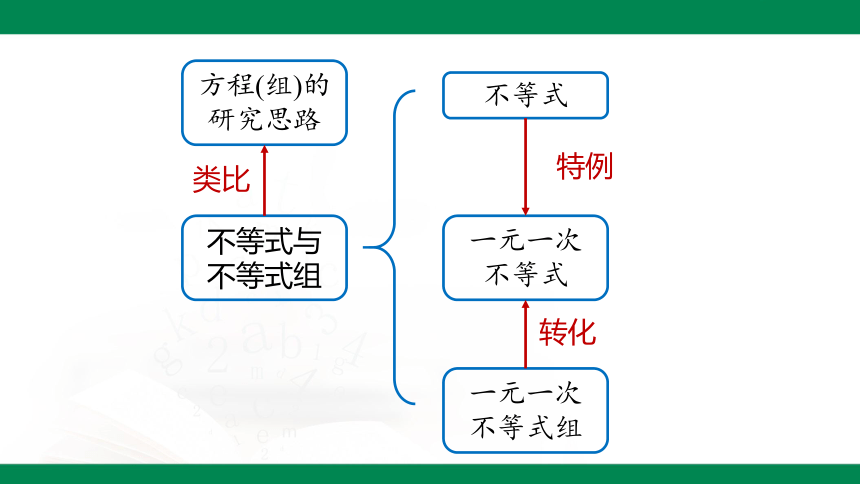
方程(组)的研究思路
不等式与不等式组
不等式
一元一次不等式
一元一次不等式组
类比
转化
特例
一、不等式
定义:用不等号“<”“>”或“≤”“≥ ”表示不等关系的式子,叫做不等式.
不等式的解:使不等式成立的未知数的值.
包含
不等式的解集:一个不等式的所有解,组成这个不等式的解的集合.
解不等式:求不等式的解集的过程.
一、不等式
基本性质1:如果a>b,那么a±c>b±c.
基本性质2:如果a>b,并且c>0,那么ac>bc(或>).
基本性质3:如果a>b,并且c<0,那么ac对称性:如果a>b,那么b传递性:如果a>b,b>c,那么a>c.
不等式的性质
解析: A.m>n两边减2,不等号方向不变,m-2>n-2;
B.m>n两边乘-4,不等号方向改变,-4m<-4n;
C.ac2>bc2两边除以c2,不等号方向不变, a>b;
D.>两边乘c,c>0时,不等号方向不变,a>b;
c<0时,不等号方向改变,a1.下列不等式变形一定正确的是( )
A.若m>n,则m-2n,则-4m>-4n
C.若ac2>bc2,则a>b D.若>,则a>b
C
解析:
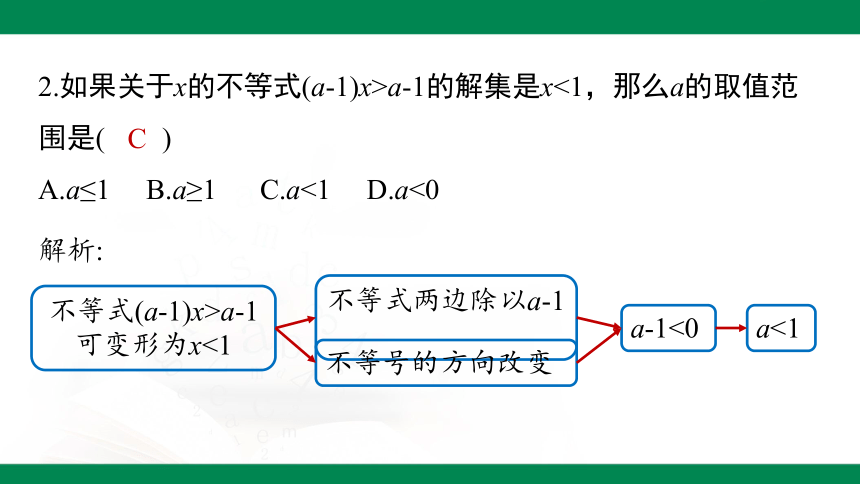
2.如果关于x的不等式(a-1)x>a-1的解集是x<1,那么a的取值范围是( )
A.a≤1 B.a≥1 C.a<1 D.a<0
C
不等式(a-1)x>a-1可变形为x<1
不等式两边除以a-1
不等号的方向改变
a-1<0
a<1
二、一元一次不等式
定义:只含有一个未知数、左右两边都是整式,并且未知数的次数都是1的不等式.
解法: 去分母
去括号
移项
合并同类项
未知数的系数化为1
不要漏乘不含分母的项
不要忘记变号
注意系数的正负,确定不等号方向是否改变
二、一元一次不等式
实际应用:①审;②设;③列;④解;⑤验;⑥答.
解析:
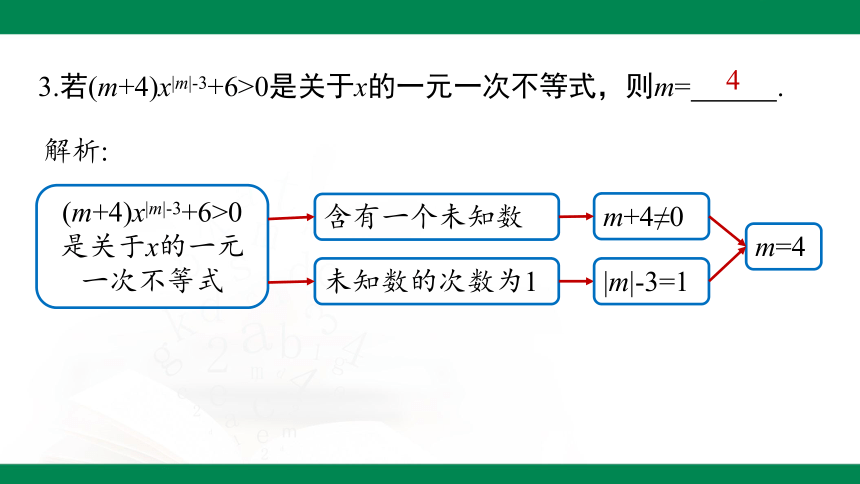
3.若(m+4)x|m|-3+6>0是关于x的一元一次不等式,则m= .
4
(m+4)x|m|-3+6>0是关于x的一元一次不等式
含有一个未知数
未知数的次数为1
m+4≠0
m=4
|m|-3=1
三、一元一次不等式组
定义:把两个(或两个以上)含有相同未知数的一元一次不等式合在一起,就得到一个一元一次不等式组.
不等式组的解集:不等式组中几个不等式的解集的公共部分,叫做这个不等式组的解集
三、一元一次不等式组
不等式组解集的确定:数轴法
口诀法:同大取大,同小取小,
大小小大中间找
大大小小无处找
解一元一次不等式组的步骤:
(1)分别求出不等式组中各个不等式的解集;(2)求出各个不等式的解集的公共部分;(3)写出不等式组的解集.
解:(1)解不等式①,得x≤4.
解不等式②,得 x>-1.
∴不等式组的解集为-1不等式组的解集在数轴上表示如图所示.
8. 解下列不等式组,并把解集在数轴上表示出来.
①
②
2
4
-1
0
1
3
5
6
7
8
9
(1)
考点1 不等式的基本性质
1. [2024广州] 若 ,则( )
D
A. B.
C. D.
2. 已知 ,则下列结论正确的是( )
B
A. B.
C. D.
返回
考点2 不等式的解及解集
3. 下列不等式 的解集在数轴上的表示,正确的是 ( )
C
A.
B.
C.
D.
返回
4. [2024吉林模拟] 下列说法正确的是( )
D
A. 不等式的解是
B. 不等式的解是
C. 是不等式 的一个解
D. 是不等式 的一个解
返回
考点3 解不等式
5.解不等式: .
【解】去分母,得 ,
移项,得,合并同类项,得 ,
不等式的两边都除以,得 .
返回
6.[2024连云港] 解不等式 ,并把解集在数轴上表
示出来.
【解】,去分母,得 ,
去括号,得,移项,得 ,
合并同类项,得 .
这个不等式的解集在数轴上表示如图.
返回
考点4 解不等式组
7. 关于的不等式组 的整数解仅有4个,则
的取值范围是( )
A
A. B.
C. D.
返回
8.[2024兰州] 解不等式组:
【解】由①,得,由②,得 .
不等式组的解集为 .
返回
9.[2024济南] 解不等式组 并写出它的所有
整数解.
【解】解不等式①,得,解不等式②,得 ,
不等式组的解集为 .
解集在数轴上表示如图.
不等式组的所有整数解为0,1,2,3.
返回
考点5 一元一次不等式(组)的应用
10.象征吉祥富贵的丁香花是西宁市市花.为美化丁香大道,
园林局准备购买某种规格的丁香花,若每棵6元,总费用不
超过5 000元,则最多可以购买_____棵丁香花.
833
【点拨】设购买 棵丁香花,
根据题意,得,解得 ,
为整数, 的最大值为833,
最多可以购买833棵丁香花.
返回
11. 为响应国家节能减排的倡议,某汽车专
卖店销售,两种型号的新能源汽车,型汽车的售价比
型汽车售价高8万元,本周售出1辆型汽车和3辆 型汽车,
销售总额为96万元.
(1)求每辆型汽车和 型汽车的售价.
【解】设每辆型汽车的售价是万元,每辆 型汽车的售价
是 万元,
根据题意,得解得
答:每辆型汽车的售价是18万元,每辆 型汽车的售价是26
万元.
(2)随着新能源汽车越来越受消费者认可,汽车专卖店计
划下周销售, 两种型号的汽车共10辆,若销售总额不少于
228万元,求 型汽车至少销售多少辆?
【解】设销售型汽车辆,则销售型汽车 辆,
根据题意,得 ,
解得, 的最小值为6.
答: 型汽车至少销售6辆.
返回
12.某中学组织学生研学,原计划租用可坐乘客45人的 种客
车若干辆,则有30人没有座位;若租用可坐乘客60人的 种
客车,则可少租6辆,且恰好坐满.
(1)求原计划租用 种客车多少辆?这次研学去了多少人?
【解】设原计划租用种客车 辆,则这次研学去了
人,
根据题意,得,解得 ,
.
答:原计划租用 种客车26辆,这次研学去了1 200人.
(2)若该校计划租用,两种客车共25辆,要求 种客车
不超过7辆,且每人都有座位,则有哪几种租车方案?
【解】设租用种客车辆,则租用种客车 辆,
根据题意,得
解得,为正整数, 的值可以为5,6,7,
该学校有3种租车方案:
方案1:租用5辆种客车,20辆 种客车;
方案2:租用6辆种客车,19辆 种客车;
方案3:租用7辆种客车,18辆 种客车.
(3)在(2)的条件下,若种客车租金为每辆220元, 种
客车租金每辆300元,应该怎样租车才最合算?
【解】选择方案1的总租金为 (元);
选择方案2的总租金为 (元);
选择方案3的总租金为 (元).
元元 元,
租用5辆种客车,20辆 种客车最合算.
返回
思想1 数形结合思想
13.如图,在数轴上,点,表示的数分别为 ,
,且点在点 的左侧.
(1)求 的取值范围;
【解】由题意,得 ,
移项、合并同类项,得 ,
两边都除以5,得 ,
的取值范围是 .
(2)若表示的数是的点在点和点之间,求 的
取值范围.
【解】由题意,得解不等式①,得 ,
解不等式②,得 ,
该不等式组的解集为 ,
由(1)得,的取值范围是 .
返回
思想2 分类讨论思想
14. 若一个不等式组 有解且解集为
,则称为的解集中点值,若 的解集中
点值是不等式组 的解(即中点值满足不等式组),则称不
等式组对于不等式组 中点包含.
(1)已知关于的不等式组 以及不等式组
,请判断不等式组对于不等式组 是否中点
包含,并写出判断过程;
【解】不等式组对于不等式组 中点包含.判断过程如下:
解不等式组得 ,
的解集中点值为5.
又是不等式组 的解,
不等式组对于不等式组 中点包含.
(2)已知关于的不等式组 和不等式
组若不等式组对于不等式组 中点包含,
求 的取值范围;
不等式组对于不等式组 中点包含,
不等式组和不等式组 有解,
解不等式组得
解不等式组得
解得 ,
当时,不等式组的解集为 ,
不等式组的解集为 ,
不等式组的解集中点值为 .
不等式组对于不等式组 中点包含,
,解得 .
又, .
(3)关于的不等式组 和不等式组
若不等式组对于不等式组 中点包含,且
所有符合要求的整数之和为14,求 的取值范围.
【解】解不等式组,得,解不等式组 ,得
, 不等式组的解集中点值为 .
又 不等式组对于不等式组 中点包含,
,可得 .
所有符合要求的整数 之和为14,
整数可取2,3,4,5,或整数可取 ,0,1,2,3,
4,或 .
返回
谢谢观看!
章末复习
第7章 一元一次不等式
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
方程(组)的研究思路
不等式与不等式组
不等式
一元一次不等式
一元一次不等式组
类比
转化
特例
一、不等式
定义:用不等号“<”“>”或“≤”“≥ ”表示不等关系的式子,叫做不等式.
不等式的解:使不等式成立的未知数的值.
包含
不等式的解集:一个不等式的所有解,组成这个不等式的解的集合.
解不等式:求不等式的解集的过程.
一、不等式
基本性质1:如果a>b,那么a±c>b±c.
基本性质2:如果a>b,并且c>0,那么ac>bc(或>).
基本性质3:如果a>b,并且c<0,那么ac
不等式的性质
解析: A.m>n两边减2,不等号方向不变,m-2>n-2;
B.m>n两边乘-4,不等号方向改变,-4m<-4n;
C.ac2>bc2两边除以c2,不等号方向不变, a>b;
D.>两边乘c,c>0时,不等号方向不变,a>b;
c<0时,不等号方向改变,a
A.若m>n,则m-2
C.若ac2>bc2,则a>b D.若>,则a>b
C
解析:
2.如果关于x的不等式(a-1)x>a-1的解集是x<1,那么a的取值范围是( )
A.a≤1 B.a≥1 C.a<1 D.a<0
C
不等式(a-1)x>a-1可变形为x<1
不等式两边除以a-1
不等号的方向改变
a-1<0
a<1
二、一元一次不等式
定义:只含有一个未知数、左右两边都是整式,并且未知数的次数都是1的不等式.
解法: 去分母
去括号
移项
合并同类项
未知数的系数化为1
不要漏乘不含分母的项
不要忘记变号
注意系数的正负,确定不等号方向是否改变
二、一元一次不等式
实际应用:①审;②设;③列;④解;⑤验;⑥答.
解析:
3.若(m+4)x|m|-3+6>0是关于x的一元一次不等式,则m= .
4
(m+4)x|m|-3+6>0是关于x的一元一次不等式
含有一个未知数
未知数的次数为1
m+4≠0
m=4
|m|-3=1
三、一元一次不等式组
定义:把两个(或两个以上)含有相同未知数的一元一次不等式合在一起,就得到一个一元一次不等式组.
不等式组的解集:不等式组中几个不等式的解集的公共部分,叫做这个不等式组的解集
三、一元一次不等式组
不等式组解集的确定:数轴法
口诀法:同大取大,同小取小,
大小小大中间找
大大小小无处找
解一元一次不等式组的步骤:
(1)分别求出不等式组中各个不等式的解集;(2)求出各个不等式的解集的公共部分;(3)写出不等式组的解集.
解:(1)解不等式①,得x≤4.
解不等式②,得 x>-1.
∴不等式组的解集为-1
8. 解下列不等式组,并把解集在数轴上表示出来.
①
②
2
4
-1
0
1
3
5
6
7
8
9
(1)
考点1 不等式的基本性质
1. [2024广州] 若 ,则( )
D
A. B.
C. D.
2. 已知 ,则下列结论正确的是( )
B
A. B.
C. D.
返回
考点2 不等式的解及解集
3. 下列不等式 的解集在数轴上的表示,正确的是 ( )
C
A.
B.
C.
D.
返回
4. [2024吉林模拟] 下列说法正确的是( )
D
A. 不等式的解是
B. 不等式的解是
C. 是不等式 的一个解
D. 是不等式 的一个解
返回
考点3 解不等式
5.解不等式: .
【解】去分母,得 ,
移项,得,合并同类项,得 ,
不等式的两边都除以,得 .
返回
6.[2024连云港] 解不等式 ,并把解集在数轴上表
示出来.
【解】,去分母,得 ,
去括号,得,移项,得 ,
合并同类项,得 .
这个不等式的解集在数轴上表示如图.
返回
考点4 解不等式组
7. 关于的不等式组 的整数解仅有4个,则
的取值范围是( )
A
A. B.
C. D.
返回
8.[2024兰州] 解不等式组:
【解】由①,得,由②,得 .
不等式组的解集为 .
返回
9.[2024济南] 解不等式组 并写出它的所有
整数解.
【解】解不等式①,得,解不等式②,得 ,
不等式组的解集为 .
解集在数轴上表示如图.
不等式组的所有整数解为0,1,2,3.
返回
考点5 一元一次不等式(组)的应用
10.象征吉祥富贵的丁香花是西宁市市花.为美化丁香大道,
园林局准备购买某种规格的丁香花,若每棵6元,总费用不
超过5 000元,则最多可以购买_____棵丁香花.
833
【点拨】设购买 棵丁香花,
根据题意,得,解得 ,
为整数, 的最大值为833,
最多可以购买833棵丁香花.
返回
11. 为响应国家节能减排的倡议,某汽车专
卖店销售,两种型号的新能源汽车,型汽车的售价比
型汽车售价高8万元,本周售出1辆型汽车和3辆 型汽车,
销售总额为96万元.
(1)求每辆型汽车和 型汽车的售价.
【解】设每辆型汽车的售价是万元,每辆 型汽车的售价
是 万元,
根据题意,得解得
答:每辆型汽车的售价是18万元,每辆 型汽车的售价是26
万元.
(2)随着新能源汽车越来越受消费者认可,汽车专卖店计
划下周销售, 两种型号的汽车共10辆,若销售总额不少于
228万元,求 型汽车至少销售多少辆?
【解】设销售型汽车辆,则销售型汽车 辆,
根据题意,得 ,
解得, 的最小值为6.
答: 型汽车至少销售6辆.
返回
12.某中学组织学生研学,原计划租用可坐乘客45人的 种客
车若干辆,则有30人没有座位;若租用可坐乘客60人的 种
客车,则可少租6辆,且恰好坐满.
(1)求原计划租用 种客车多少辆?这次研学去了多少人?
【解】设原计划租用种客车 辆,则这次研学去了
人,
根据题意,得,解得 ,
.
答:原计划租用 种客车26辆,这次研学去了1 200人.
(2)若该校计划租用,两种客车共25辆,要求 种客车
不超过7辆,且每人都有座位,则有哪几种租车方案?
【解】设租用种客车辆,则租用种客车 辆,
根据题意,得
解得,为正整数, 的值可以为5,6,7,
该学校有3种租车方案:
方案1:租用5辆种客车,20辆 种客车;
方案2:租用6辆种客车,19辆 种客车;
方案3:租用7辆种客车,18辆 种客车.
(3)在(2)的条件下,若种客车租金为每辆220元, 种
客车租金每辆300元,应该怎样租车才最合算?
【解】选择方案1的总租金为 (元);
选择方案2的总租金为 (元);
选择方案3的总租金为 (元).
元元 元,
租用5辆种客车,20辆 种客车最合算.
返回
思想1 数形结合思想
13.如图,在数轴上,点,表示的数分别为 ,
,且点在点 的左侧.
(1)求 的取值范围;
【解】由题意,得 ,
移项、合并同类项,得 ,
两边都除以5,得 ,
的取值范围是 .
(2)若表示的数是的点在点和点之间,求 的
取值范围.
【解】由题意,得解不等式①,得 ,
解不等式②,得 ,
该不等式组的解集为 ,
由(1)得,的取值范围是 .
返回
思想2 分类讨论思想
14. 若一个不等式组 有解且解集为
,则称为的解集中点值,若 的解集中
点值是不等式组 的解(即中点值满足不等式组),则称不
等式组对于不等式组 中点包含.
(1)已知关于的不等式组 以及不等式组
,请判断不等式组对于不等式组 是否中点
包含,并写出判断过程;
【解】不等式组对于不等式组 中点包含.判断过程如下:
解不等式组得 ,
的解集中点值为5.
又是不等式组 的解,
不等式组对于不等式组 中点包含.
(2)已知关于的不等式组 和不等式
组若不等式组对于不等式组 中点包含,
求 的取值范围;
不等式组对于不等式组 中点包含,
不等式组和不等式组 有解,
解不等式组得
解不等式组得
解得 ,
当时,不等式组的解集为 ,
不等式组的解集为 ,
不等式组的解集中点值为 .
不等式组对于不等式组 中点包含,
,解得 .
又, .
(3)关于的不等式组 和不等式组
若不等式组对于不等式组 中点包含,且
所有符合要求的整数之和为14,求 的取值范围.
【解】解不等式组,得,解不等式组 ,得
, 不等式组的解集中点值为 .
又 不等式组对于不等式组 中点包含,
,可得 .
所有符合要求的整数 之和为14,
整数可取2,3,4,5,或整数可取 ,0,1,2,3,
4,或 .
返回
谢谢观看!
