第三单元专项练习11:八种问题其七求不规则或组合立体图形的表面积和体积问题(含解析)-2024-2025学年六年级数学下册典型例题(人教版)
文档属性
| 名称 | 第三单元专项练习11:八种问题其七求不规则或组合立体图形的表面积和体积问题(含解析)-2024-2025学年六年级数学下册典型例题(人教版) |  | |
| 格式 | doc | ||
| 文件大小 | 759.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-09 15:25:03 | ||
图片预览



文档简介
/ 让教学更有效 精品试卷 | 数学学科
第三单元专项练习11:
八种问题其七.求不规则或组合立体图形的表面积和体积问题
第一部分含圆柱
1.求下图立体图形的表面积。(单位:厘米)
2.计算下面图形的表面积。
3.求下图所示几何体的表面积(单位:)。
4.计算下面图形的表面积和体积。
5.计算下面圆柱的表面积和体积。(单位:厘米)
6.毕业季,美术老师教学生用卡纸自制“博士帽”(帽穗除外)。如图:上面是边长为30厘米的正方形,下面是底面直径为18厘米,高为20厘米的无盖无底的圆柱。制作1个这样的“博士帽”,至少需要卡纸多少平方厘米?21·cn·jy·com
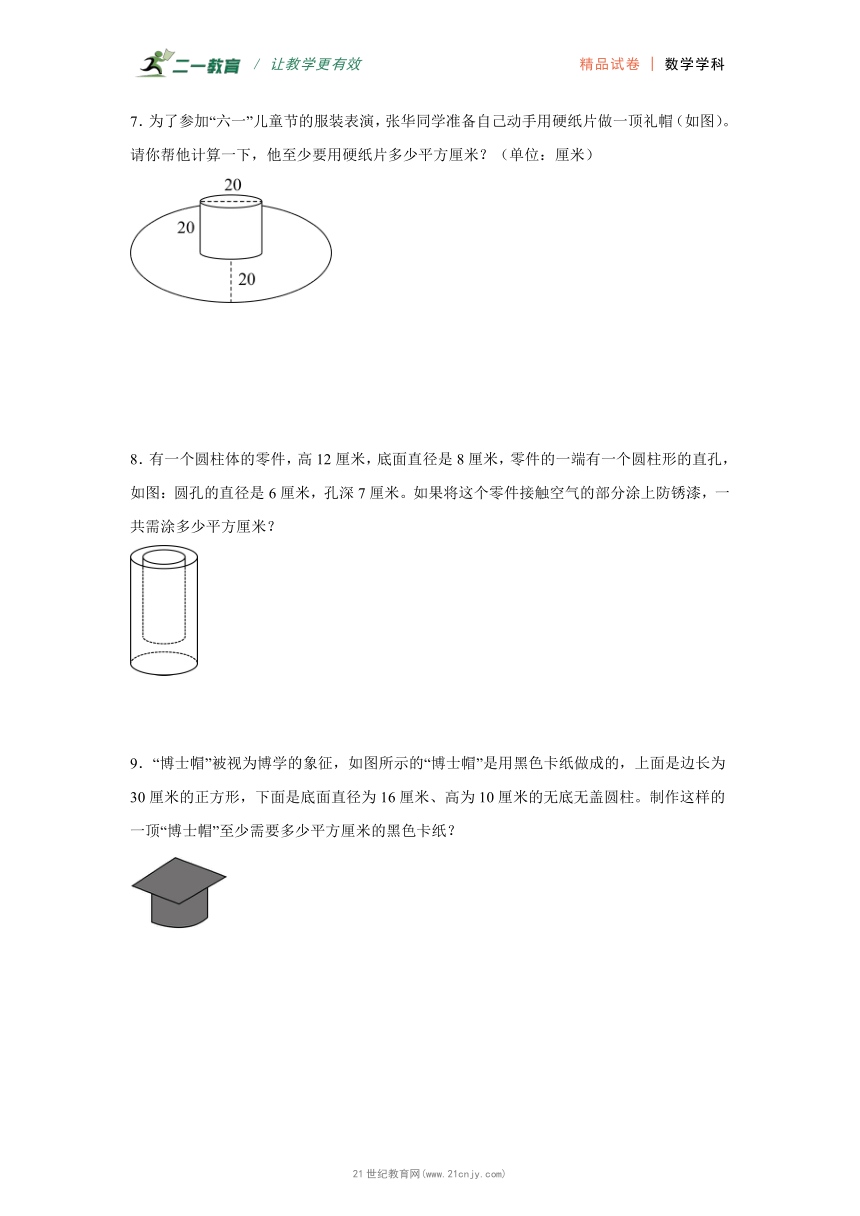
7.为了参加“六一”儿童节的服装表演,张华同学准备自己动手用硬纸片做一顶礼帽(如图)。请你帮他计算一下,他至少要用硬纸片多少平方厘米?(单位:厘米)
8.有一个圆柱体的零件,高12厘米,底面直径是8厘米,零件的一端有一个圆柱形的直孔,如图:圆孔的直径是6厘米,孔深7厘米。如果将这个零件接触空气的部分涂上防锈漆,一共需涂多少平方厘米?【来源:21cnj*y.co*m】
9.“博士帽”被视为博学的象征,如图所示的“博士帽”是用黑色卡纸做成的,上面是边长为30厘米的正方形,下面是底面直径为16厘米、高为10厘米的无底无盖圆柱。制作这样的一顶“博士帽”至少需要多少平方厘米的黑色卡纸?【版权所有:21教育】
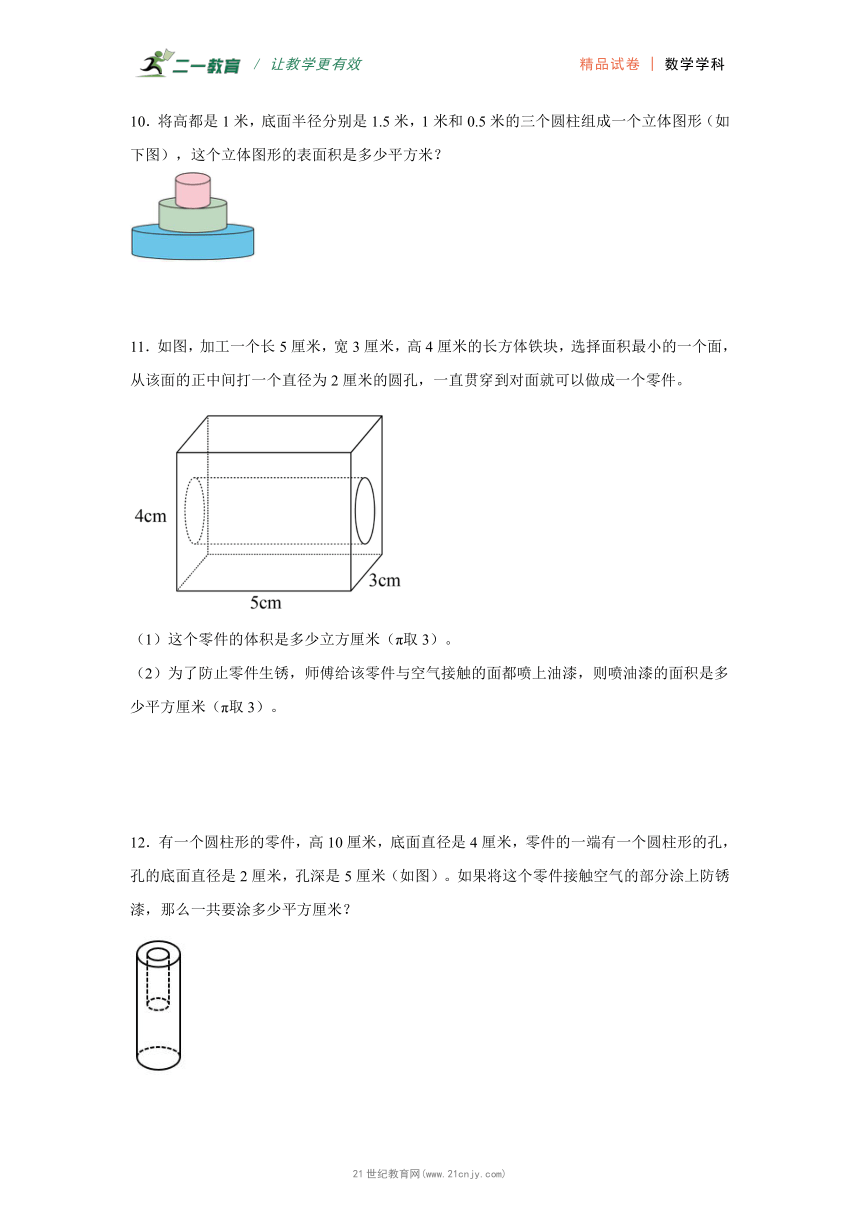
10.将高都是1米,底面半径分别是1.5米,1米和0.5米的三个圆柱组成一个立体图形(如下图),这个立体图形的表面积是多少平方米?
11.如图,加工一个长5厘米,宽3厘米,高4厘米的长方体铁块,选择面积最小的一个面,从该面的正中间打一个直径为2厘米的圆孔,一直贯穿到对面就可以做成一个零件。
(1)这个零件的体积是多少立方厘米(π取3)。
(2)为了防止零件生锈,师傅给该零件与空气接触的面都喷上油漆,则喷油漆的面积是多少平方厘米(π取3)。21·世纪*教育网
12.有一个圆柱形的零件,高10厘米,底面直径是4厘米,零件的一端有一个圆柱形的孔,孔的底面直径是2厘米,孔深是5厘米(如图)。如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?
第二部分含圆锥
13.一个圆柱截掉一部分后如图所示,求图中立体图形的体积。(单位:厘米)
14.第一个图(单位:cm)求表面积,第二个图求体积。
15.求组合图形的体积。(单位:cm)
16.求体积。(单位:厘米)
求圆柱中间挖去一个圆锥剩下的体积。
17.求组合体的体积。(单位:cm)
18.求下面图形的体积。(左图中的半圆柱的底面直径是10厘米,右图是从圆柱中挖法一个圆锥后的剩余部分)。(单位:厘米)
19.一个谷囤,上面是圆锥形的,下面是圆柱形的。量得底面周长是6.28米,圆柱的高是2米,圆锥的高是0.3米。如果每立方米稻谷约重650千克,这个谷囤的稻谷约重多少千克?
20.学校科技社团小组的同学们在研究陀螺的稳定性,他们用圆柱形的木头和圆锥形的金属制作了一个陀螺(如图),你能帮助他们计算出这个陀螺的体积吗?
21.蒙古包由一个圆柱和一个圆锥组成。圆柱的底面直径是8米,高是2米;圆锥的高是1米。蒙古包所占的地面面积有多大?内部空间大约是多少立方米?21*cnjy*com
22.现在我们常用的稻谷储粮罐都是锥底的,虽然比以前的平底储粮罐工艺复杂,但优点在于底部沉淀的杂质更易清除,便于储粮罐的排污和清洗。下图是某公司设计的一款新型储粮罐,请计算出它的体积。
23.一个物体是由圆柱和圆锥黏合而成的(如图),如果把圆柱和圆锥重新分开,表面积就增加25.12平方厘米,原来这个物体的体积是多少立方厘米?(只列综合算式或方程,不计算。)
24.如图,粮囤上面是圆锥形,下面是圆柱形,圆柱的底面周长是12.56米,高是2米,圆锥的高是1.2米。一个粮囤的体积是多少立方米?
《第三单元专项练习11:八种问题其七 求不规则或组合立体图形的表面积和体积问题》参考答案
1.228.8平方厘米
【分析】观察图形可知,圆柱和长方体有重合的部分,把圆柱的上底面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而圆柱只需计算侧面积即可;
图形的表面积=圆柱的侧面积+长方体的表面积
其中,圆柱的侧面积S侧=πdh,长方体的表面积S=2(ab+ah+bh),代入数据计算求解。
【详解】圆柱的侧面积:
3.14×4×5=62.8(平方厘米)
长方体的表面积:
(7×4+7×5+4×5)×2
=(28+35+20)×2
=83×2
=166(平方厘米)
组合体的表面积:
62.8+166=228.8(平方厘米)
图形的表面积是228.8平方厘米。
2.188.4cm2
【分析】由于上面的圆柱与下面的圆柱体组合在一起,所以上面的圆柱只求侧面积,下面圆柱体求表面积,然后求和就是这个图形的表面积。根据圆柱的侧面积公式:S=πdh,圆柱的表面积=侧面积+底面积×2,把数据代入公式解答即可。
【详解】
图形的表面积是188.4cm2。
3.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
4.10228 cm2;67140 cm3
【分析】看图可知,这个立体图形的表面积=正方体的表面积+圆柱的侧面积,正方体表面积=棱长×棱长×6,圆柱的侧面积=底面周长×高。这个立体图形的体积=正方体体积+圆柱体积,正方体体积=棱长×棱长×棱长,圆柱体积=底面积×高,据此列式计算即可求出表面积和体积。【出处:21教育名师】
【详解】表面积:
40×40×6+20×3.14×10
=9600+628
=10228(cm2)
体积:
40×40×40+(20÷2)2×3.14×10
=64000+102×3.14×10
=64000+3140
=67140(cm3)
立体图形的表面积是10228cm2,体积是67140cm3。
5.表面积: 734.76平方厘米;体积: 571.48立方厘米
【分析】表面积=大圆直径是20厘米,小圆直径是6厘米的圆环面积×2+底面直径是20厘米,高是2厘米的圆柱的侧面积+底面直径是6厘米,高是2厘米的圆柱的侧面积;根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答;
体积=底面直径是20厘米,高是2厘米的圆柱的体积-底面直径是6厘米,高是2厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【详解】3.14×[(20÷2)2-(6÷2)2]×2+3.14×20×2+3.14×6×2
=3.14×[102-32]×2+62.8×2+18.84×2
=3.14×[100-9]×2+125.6+37.68
=3.14×91×2+125.6+37.68
=571.48+125.6+37.68
=734.76(平方厘米)
3.14×(20÷2)2×2-3.14×(6÷2)2×2
=3.14×102×2-3.14×32×2
=3.14×100×2-3.14×9×2
=628-56.52
=571.48(立方厘米)
6.2030.4平方厘米
【分析】看图可知,博士帽的面积=圆柱侧面积+正方形面积,圆柱侧面积=底面周长×高,正方形面积=边长×边长,据此列式解答。
【详解】3.14×18×20+30×30
=1130.4+900
=2030.4(平方厘米)
答:至少需要卡纸2030.4平方厘米。
7.4082平方厘米
【分析】帽子顶和帽檐合在一起就是一个大圆,先求出大圆的半径,然后根据圆的面积公式:S=πr2,圆柱的侧面积公式:S侧=Ch,分别计算大圆的面积和帽顶部分的侧面积,最后将两者相加就是所需硬纸片的总面积。
【详解】20÷2=10(厘米)
10+20=30(厘米)
3.14×30
=3.14×900
=2826(平方厘米)
3.14×20×20=1256(平方厘米)
2826+1256=4082(平方厘米)
答:他至少要用硬纸片4082平方厘米。
【点睛】本题关键是求出大圆的半径,明确帽檐的面积与帽顶的面积和等于大圆的面积。
8.533.8平方厘米
【分析】这个零件接触空气部分,我们既要注意圆柱体的外表面积,又要注意圆孔内的表面积,同时还要注意零件的底面是圆环。由于打孔的深度与柱体的长度不相同,所以在孔内还要有一个小圆的底面要涂上油漆,这一点不能忽略。但是,我们可以把小圆的底面与圆环拼成一个圆,这就成了原圆柱的底面。【来源:21·世纪·教育·网】
所以,这个零件接触空气的面积即涂漆面积=高12厘米,底面直径是8厘米的圆柱的表面积+直径是6厘米,高为7厘米的圆柱的侧面积。
圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高。圆的面积(底面积)=π×半径2,据此代入数据计算。
【详解】
=3.14×42×2+25.12×12+18.84×7
=3.14×16×2+301.44+131.88
=100.48+301.44+131.88
=401.92+131.88
=533.8(平方厘米)
答:一共需涂533.8平方厘米。
9.1402.4平方厘米
【分析】根据题意,这种“博士帽”的上面是正方形,下面是无盖无底的圆柱,所以制作一顶“博士帽”至少需要卡纸的面积=正方形的面积+圆柱的侧面积;根据正方形的面积公式S=a2,圆柱的侧面积公式S=πdh,代入数据计算,求出制作一顶“博士帽”至少需要卡纸的面积。
【详解】3.14×16×10+30×30
=50.24×10+900
=502.4+900
=1402.4(平方厘米)
答:制作这样的一顶“博士帽”至少需要1402.4平方厘米的黑色卡纸。
10.32.97平方米
【分析】根据题意得:立体图形由三个圆柱叠加组成,立体图形表面积=三个圆柱的侧面积之和+最下面圆柱的底面积×2,根据圆柱侧面积=,底面积=。据此计算可得出答案。21cnjy.com
【详解】最下面的圆柱侧面积为:3.14×1.5×2×1=9.42(平方米)
中间的圆柱侧面积为:3.14×1×2×1=6.28(平方米)
最上面的圆柱侧面积为:3.14×0.5×2×1=3.14(平方米)
侧面积之和为:9.42+6.28+3.14=18.84(平方米)
最下面圆柱的2个底面积为:3.14×1.52×2=14.13(平方米)
则立体图形表面积为:18.84+14.13=32.97(平方米)
答:这个立体图形的表面积是32.97平方米。
11.(1)45立方厘米
(2)118平方厘米
【分析】(1)零件体积=长方体体积-圆柱体积,长方体体积=长×宽×高,圆柱体积=底面积×高,看图可知,圆柱的高=长方体的长,据此列式解答;www.21-cn-jy.com
(2)看图可知,喷油漆的面积=长方体表面积-圆柱底面积×2+圆柱侧面积,长方体表面积=(长×宽+长×高+宽×高)×2,圆柱侧面积=底面周长×高,据此列式解答。
【详解】(1)2÷2=1(厘米)
5×3×4-3×12×5
=60-3×1×5
=60-15
=45(立方厘米)
答:这个零件的体积是45立方厘米。
(2)(5×3+5×4+3×4)×2-3×12×2+3×2×5
=(15+20+12)×2-3×1×2+30
=47×2-6+30
=94-6+30
=118(平方厘米)
答:喷油漆的面积是118平方厘米。
12.182.12平方厘米
【分析】这个零件接触空气的部分涂防锈漆的面积即这个零件的表面积,零件的表面积等于圆柱体的表面积加上圆柱形圆孔的侧面积;根据圆柱的表面积公式:表面积=底面积×2+侧面积,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【详解】3.14×(4÷2)2×2+3.14×4×10+3.14×2×5
=3.14×4×2+12.56×10+6.28×5
=12.56×2+125.6+31.4
=25.12+125.6+31.4
=150.72+31.4
=182.12(平方厘米)
答:一共要涂182.12平方厘米。
【点睛】熟练掌握圆柱的侧面积公式、圆柱的表面积公式是解答本题的关键。
13.904.32立方厘米
【分析】把这个图形看成底面直径为8厘米,高为厘米的圆柱的一半,根据圆柱体积=底面积×高,求出这个立体图形的体积即可。21*cnjy*com
【详解】高:(厘米)
立体图形体积:
(立方厘米)
立体图形的体积904.32立方厘米。
14.(1)785cm2;(2)15.7cm3
【分析】(1)根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算,即可求出圆柱的表面积。
(2)组合体的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】(1)3.14×10×20+3.14×(10÷2)2×2
=3.14×10×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(cm2)
圆柱的表面积是785cm2。
(2)3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×12×4+×3.14×12×3
=3.14×1×4+×3.14×1×3
=12.56+3.14
=15.7(cm3)
组合体的体积是15.7cm3。
15.43.96cm3
【分析】观察图形可知,该组合图形的体积=中间圆柱的体积+两边的两个圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(2÷2)2×(18-3×2)+×3.14×(2÷2)2×3×2
=3.14×12×(18-6)+×3.14×12×3×2
=3.14×12×12+×3.14×12×3×2
=3.14×1×12+×3.14×1×3×2
=37.68+6.28
=43.96(cm3)
16.2449.2立方厘米
【分析】根据圆柱的体积公式:V=πr2h,以及圆锥的体积公式:V=πr2h代入数据分别求出圆柱的体积和圆锥的体积,然后求出差,也就是剩下的体积。21教育网
【详解】3.14×(12÷2)2×25-3.14×(12÷2)2×10×
=3.14×62×25-3.14×62×10×
=3.14×36×25-3.14×36×10×
=2826-376.8
=2449.2(立方厘米)
剩下的体积是2449.2立方厘米。
17.60.56cm3
【分析】组合体是由一个长方体和一个圆锥组成,则组合体的体积=长方体的体积+圆锥的体积;
根据长方体的体积公式V=abh,圆锥的体积公式V=πr2h,代入数据计算即可求解。
【详解】长方体的体积:
4×4×3
=16×3
=48(cm3)
圆锥的体积:
×3.14×(4÷2)2×3
=×3.14×22×3
=×3.14×4×3
=12.56(cm3)
一共:48+12.56=60.56(cm3)
组合体的体积是60.56cm3。
18.7822.5立方厘米;6358.5立方厘米
【分析】观察第一个图形,是从一个长方体中截取了一个半圆柱,图形的体积=长方体的体积-半圆柱的体积,根据“V长方体=abh”“V圆柱=πr2h”,代入数据即可解答;
观察第二个图形可知:剩余部分的体积是圆柱与圆锥的体积之差,根据圆柱的体积:V=Sh,圆锥的体积公式:V=Sh,把数据分别代入公式解答即可。21世纪教育网版权所有
【详解】第一个图形的体积:
30×20×15-3.14×(10÷2)2×30÷2
=30×20×15-3.14×25×30÷2
=600×15-78.5×30÷2
=9000-2355÷2
=9000-1177.5
=7822.5(立方厘米)
它的体积是7822.5立方厘米。
第二个图形的体积:
3.14×()2×30-×3.14×()2×15
=3.14×92×30-×3.14×92×15
=3.14×81×30-×3.14×81×15
=3.14×81×30-3.14×81×5
=254.34×30-254.34×5
=7630.2-1271.7
=6358.5(立方厘米)
它的体积是6358.5立方厘米。
19.4286.1千克
【分析】分析题意可知:谷囤的体积=圆锥的体积+圆柱的体积,其中底面周长是6.28米,结合谷囤图形的特点可知:这个底面周长既是圆锥也是圆柱的底面周长,根据圆的周长=,则底面半径=底面周长÷()。圆锥的体积=,圆柱的体积=,代入数据分别计算出圆锥和圆柱的体积,进而求出谷囤的体积。又知每立方米稻谷约重650千克,则用谷囤的体积×650=这个谷囤的稻谷的总质量。据此解答即可。
【详解】6.28÷(2×3.14)
=6.28÷6.28
=1(米)
=
=
=6.28+0.314
=6.594(立方米)
6.594×650=4286.1(千克)
答:这个谷囤的稻谷约重4286.1千克。
20.471立方厘米
【分析】分析题目,陀螺是由一个圆柱体和一个圆锥体组成的,圆柱的体积=π(d÷2)2h,圆锥的体积=π(d÷2)2h,据此代入数据分别求出圆柱和圆锥的体积,再相加即可得到陀螺的体积。2·1·c·n·j·y
【详解】3.14×(10÷2)2×4
=3.14×52×4
=3.14×25×4
=78.5×4
=314(立方厘米)
3.14×(10÷2)2×6×
=3.14×52×6×
=3.14×25×6×
=78.5×6×
=471×
=157(立方厘米)
314+157=471(立方厘米)
答:这个陀螺的体积是471立方厘米。
21.50.24平方米;117立方米
【分析】根据题意得:蒙古包占地面积是圆柱底面积,圆柱底面直径为8米,则底面圆面积=;内部空间即为这个蒙古包的容积,蒙古包由一个圆锥和一个圆柱组成,则体积为两者之和,即,h1表示圆柱高度,h2表示圆锥高度,据此计算可得出答案。2-1-c-n-j-y
【详解】蒙古包占地面积为:
3.14×(8÷2)2
=3.14×42
=50.24(平方米)
内部空间大小为:
(立方米)
答:蒙古包所占的地面面积有50.24平方米;内部空间大约是117立方米。
22.5.652立方米
【分析】由图可知,新型储粮罐的体积=底面直径为2米,高0.9米的圆锥体积+底面直径为2米,高1.5米的圆锥体积+底面直径为2米,高1米的圆柱体积,根据圆柱的体积=πr2h,圆锥的体积=πr2h,代入数据解答即可。www-2-1-cnjy-com
【详解】2÷2=1(米)
3.14×12×0.9×+3.14×12×1+3.14×12×1.5×
=3.14×0.9×+3.14+3.14×1.5×
=2.826×+3.14+4.71×
=0.942+3.14+1.57
=4.082+1.57
=5.652(立方米)
答:新型储粮罐的体积是5.652立方米。
23.25.12÷2×3+25.12÷2×3×
【分析】如果把圆柱和圆锥重新分开,则表面积增加2个底面积,圆柱和圆锥的底面积相同,用25.12÷2即可求出每个底面积;然后根据圆柱的体积=底面积×高,圆锥的体积=底面积×高×,代入数据分别求出圆柱和圆锥的体积,再相加即可。21教育名师原创作品
【详解】25.12÷2×3+25.12÷2×3×
=37.68+12.56
=50.24(立方厘米)
答:原来这个物体的体积是50.24立方厘米。
24.30.144立方米
【分析】
粮囤的体积可以看作是一个圆柱的体积加上一个圆锥的体积,其中圆柱的底面积和圆锥的底面积相等,根据圆柱的体积=底面积×高,圆锥的体积=×底面积×高,代入相应数值计算,据此解答。
【详解】
底面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方米)
(立方米)
答:一个粮囤的体积是30.144立方米。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第三单元专项练习11:
八种问题其七.求不规则或组合立体图形的表面积和体积问题
第一部分含圆柱
1.求下图立体图形的表面积。(单位:厘米)
2.计算下面图形的表面积。
3.求下图所示几何体的表面积(单位:)。
4.计算下面图形的表面积和体积。
5.计算下面圆柱的表面积和体积。(单位:厘米)
6.毕业季,美术老师教学生用卡纸自制“博士帽”(帽穗除外)。如图:上面是边长为30厘米的正方形,下面是底面直径为18厘米,高为20厘米的无盖无底的圆柱。制作1个这样的“博士帽”,至少需要卡纸多少平方厘米?21·cn·jy·com
7.为了参加“六一”儿童节的服装表演,张华同学准备自己动手用硬纸片做一顶礼帽(如图)。请你帮他计算一下,他至少要用硬纸片多少平方厘米?(单位:厘米)
8.有一个圆柱体的零件,高12厘米,底面直径是8厘米,零件的一端有一个圆柱形的直孔,如图:圆孔的直径是6厘米,孔深7厘米。如果将这个零件接触空气的部分涂上防锈漆,一共需涂多少平方厘米?【来源:21cnj*y.co*m】
9.“博士帽”被视为博学的象征,如图所示的“博士帽”是用黑色卡纸做成的,上面是边长为30厘米的正方形,下面是底面直径为16厘米、高为10厘米的无底无盖圆柱。制作这样的一顶“博士帽”至少需要多少平方厘米的黑色卡纸?【版权所有:21教育】
10.将高都是1米,底面半径分别是1.5米,1米和0.5米的三个圆柱组成一个立体图形(如下图),这个立体图形的表面积是多少平方米?
11.如图,加工一个长5厘米,宽3厘米,高4厘米的长方体铁块,选择面积最小的一个面,从该面的正中间打一个直径为2厘米的圆孔,一直贯穿到对面就可以做成一个零件。
(1)这个零件的体积是多少立方厘米(π取3)。
(2)为了防止零件生锈,师傅给该零件与空气接触的面都喷上油漆,则喷油漆的面积是多少平方厘米(π取3)。21·世纪*教育网
12.有一个圆柱形的零件,高10厘米,底面直径是4厘米,零件的一端有一个圆柱形的孔,孔的底面直径是2厘米,孔深是5厘米(如图)。如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?
第二部分含圆锥
13.一个圆柱截掉一部分后如图所示,求图中立体图形的体积。(单位:厘米)
14.第一个图(单位:cm)求表面积,第二个图求体积。
15.求组合图形的体积。(单位:cm)
16.求体积。(单位:厘米)
求圆柱中间挖去一个圆锥剩下的体积。
17.求组合体的体积。(单位:cm)
18.求下面图形的体积。(左图中的半圆柱的底面直径是10厘米,右图是从圆柱中挖法一个圆锥后的剩余部分)。(单位:厘米)
19.一个谷囤,上面是圆锥形的,下面是圆柱形的。量得底面周长是6.28米,圆柱的高是2米,圆锥的高是0.3米。如果每立方米稻谷约重650千克,这个谷囤的稻谷约重多少千克?
20.学校科技社团小组的同学们在研究陀螺的稳定性,他们用圆柱形的木头和圆锥形的金属制作了一个陀螺(如图),你能帮助他们计算出这个陀螺的体积吗?
21.蒙古包由一个圆柱和一个圆锥组成。圆柱的底面直径是8米,高是2米;圆锥的高是1米。蒙古包所占的地面面积有多大?内部空间大约是多少立方米?21*cnjy*com
22.现在我们常用的稻谷储粮罐都是锥底的,虽然比以前的平底储粮罐工艺复杂,但优点在于底部沉淀的杂质更易清除,便于储粮罐的排污和清洗。下图是某公司设计的一款新型储粮罐,请计算出它的体积。
23.一个物体是由圆柱和圆锥黏合而成的(如图),如果把圆柱和圆锥重新分开,表面积就增加25.12平方厘米,原来这个物体的体积是多少立方厘米?(只列综合算式或方程,不计算。)
24.如图,粮囤上面是圆锥形,下面是圆柱形,圆柱的底面周长是12.56米,高是2米,圆锥的高是1.2米。一个粮囤的体积是多少立方米?
《第三单元专项练习11:八种问题其七 求不规则或组合立体图形的表面积和体积问题》参考答案
1.228.8平方厘米
【分析】观察图形可知,圆柱和长方体有重合的部分,把圆柱的上底面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而圆柱只需计算侧面积即可;
图形的表面积=圆柱的侧面积+长方体的表面积
其中,圆柱的侧面积S侧=πdh,长方体的表面积S=2(ab+ah+bh),代入数据计算求解。
【详解】圆柱的侧面积:
3.14×4×5=62.8(平方厘米)
长方体的表面积:
(7×4+7×5+4×5)×2
=(28+35+20)×2
=83×2
=166(平方厘米)
组合体的表面积:
62.8+166=228.8(平方厘米)
图形的表面积是228.8平方厘米。
2.188.4cm2
【分析】由于上面的圆柱与下面的圆柱体组合在一起,所以上面的圆柱只求侧面积,下面圆柱体求表面积,然后求和就是这个图形的表面积。根据圆柱的侧面积公式:S=πdh,圆柱的表面积=侧面积+底面积×2,把数据代入公式解答即可。
【详解】
图形的表面积是188.4cm2。
3.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
4.10228 cm2;67140 cm3
【分析】看图可知,这个立体图形的表面积=正方体的表面积+圆柱的侧面积,正方体表面积=棱长×棱长×6,圆柱的侧面积=底面周长×高。这个立体图形的体积=正方体体积+圆柱体积,正方体体积=棱长×棱长×棱长,圆柱体积=底面积×高,据此列式计算即可求出表面积和体积。【出处:21教育名师】
【详解】表面积:
40×40×6+20×3.14×10
=9600+628
=10228(cm2)
体积:
40×40×40+(20÷2)2×3.14×10
=64000+102×3.14×10
=64000+3140
=67140(cm3)
立体图形的表面积是10228cm2,体积是67140cm3。
5.表面积: 734.76平方厘米;体积: 571.48立方厘米
【分析】表面积=大圆直径是20厘米,小圆直径是6厘米的圆环面积×2+底面直径是20厘米,高是2厘米的圆柱的侧面积+底面直径是6厘米,高是2厘米的圆柱的侧面积;根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答;
体积=底面直径是20厘米,高是2厘米的圆柱的体积-底面直径是6厘米,高是2厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
【详解】3.14×[(20÷2)2-(6÷2)2]×2+3.14×20×2+3.14×6×2
=3.14×[102-32]×2+62.8×2+18.84×2
=3.14×[100-9]×2+125.6+37.68
=3.14×91×2+125.6+37.68
=571.48+125.6+37.68
=734.76(平方厘米)
3.14×(20÷2)2×2-3.14×(6÷2)2×2
=3.14×102×2-3.14×32×2
=3.14×100×2-3.14×9×2
=628-56.52
=571.48(立方厘米)
6.2030.4平方厘米
【分析】看图可知,博士帽的面积=圆柱侧面积+正方形面积,圆柱侧面积=底面周长×高,正方形面积=边长×边长,据此列式解答。
【详解】3.14×18×20+30×30
=1130.4+900
=2030.4(平方厘米)
答:至少需要卡纸2030.4平方厘米。
7.4082平方厘米
【分析】帽子顶和帽檐合在一起就是一个大圆,先求出大圆的半径,然后根据圆的面积公式:S=πr2,圆柱的侧面积公式:S侧=Ch,分别计算大圆的面积和帽顶部分的侧面积,最后将两者相加就是所需硬纸片的总面积。
【详解】20÷2=10(厘米)
10+20=30(厘米)
3.14×30
=3.14×900
=2826(平方厘米)
3.14×20×20=1256(平方厘米)
2826+1256=4082(平方厘米)
答:他至少要用硬纸片4082平方厘米。
【点睛】本题关键是求出大圆的半径,明确帽檐的面积与帽顶的面积和等于大圆的面积。
8.533.8平方厘米
【分析】这个零件接触空气部分,我们既要注意圆柱体的外表面积,又要注意圆孔内的表面积,同时还要注意零件的底面是圆环。由于打孔的深度与柱体的长度不相同,所以在孔内还要有一个小圆的底面要涂上油漆,这一点不能忽略。但是,我们可以把小圆的底面与圆环拼成一个圆,这就成了原圆柱的底面。【来源:21·世纪·教育·网】
所以,这个零件接触空气的面积即涂漆面积=高12厘米,底面直径是8厘米的圆柱的表面积+直径是6厘米,高为7厘米的圆柱的侧面积。
圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高。圆的面积(底面积)=π×半径2,据此代入数据计算。
【详解】
=3.14×42×2+25.12×12+18.84×7
=3.14×16×2+301.44+131.88
=100.48+301.44+131.88
=401.92+131.88
=533.8(平方厘米)
答:一共需涂533.8平方厘米。
9.1402.4平方厘米
【分析】根据题意,这种“博士帽”的上面是正方形,下面是无盖无底的圆柱,所以制作一顶“博士帽”至少需要卡纸的面积=正方形的面积+圆柱的侧面积;根据正方形的面积公式S=a2,圆柱的侧面积公式S=πdh,代入数据计算,求出制作一顶“博士帽”至少需要卡纸的面积。
【详解】3.14×16×10+30×30
=50.24×10+900
=502.4+900
=1402.4(平方厘米)
答:制作这样的一顶“博士帽”至少需要1402.4平方厘米的黑色卡纸。
10.32.97平方米
【分析】根据题意得:立体图形由三个圆柱叠加组成,立体图形表面积=三个圆柱的侧面积之和+最下面圆柱的底面积×2,根据圆柱侧面积=,底面积=。据此计算可得出答案。21cnjy.com
【详解】最下面的圆柱侧面积为:3.14×1.5×2×1=9.42(平方米)
中间的圆柱侧面积为:3.14×1×2×1=6.28(平方米)
最上面的圆柱侧面积为:3.14×0.5×2×1=3.14(平方米)
侧面积之和为:9.42+6.28+3.14=18.84(平方米)
最下面圆柱的2个底面积为:3.14×1.52×2=14.13(平方米)
则立体图形表面积为:18.84+14.13=32.97(平方米)
答:这个立体图形的表面积是32.97平方米。
11.(1)45立方厘米
(2)118平方厘米
【分析】(1)零件体积=长方体体积-圆柱体积,长方体体积=长×宽×高,圆柱体积=底面积×高,看图可知,圆柱的高=长方体的长,据此列式解答;www.21-cn-jy.com
(2)看图可知,喷油漆的面积=长方体表面积-圆柱底面积×2+圆柱侧面积,长方体表面积=(长×宽+长×高+宽×高)×2,圆柱侧面积=底面周长×高,据此列式解答。
【详解】(1)2÷2=1(厘米)
5×3×4-3×12×5
=60-3×1×5
=60-15
=45(立方厘米)
答:这个零件的体积是45立方厘米。
(2)(5×3+5×4+3×4)×2-3×12×2+3×2×5
=(15+20+12)×2-3×1×2+30
=47×2-6+30
=94-6+30
=118(平方厘米)
答:喷油漆的面积是118平方厘米。
12.182.12平方厘米
【分析】这个零件接触空气的部分涂防锈漆的面积即这个零件的表面积,零件的表面积等于圆柱体的表面积加上圆柱形圆孔的侧面积;根据圆柱的表面积公式:表面积=底面积×2+侧面积,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【详解】3.14×(4÷2)2×2+3.14×4×10+3.14×2×5
=3.14×4×2+12.56×10+6.28×5
=12.56×2+125.6+31.4
=25.12+125.6+31.4
=150.72+31.4
=182.12(平方厘米)
答:一共要涂182.12平方厘米。
【点睛】熟练掌握圆柱的侧面积公式、圆柱的表面积公式是解答本题的关键。
13.904.32立方厘米
【分析】把这个图形看成底面直径为8厘米,高为厘米的圆柱的一半,根据圆柱体积=底面积×高,求出这个立体图形的体积即可。21*cnjy*com
【详解】高:(厘米)
立体图形体积:
(立方厘米)
立体图形的体积904.32立方厘米。
14.(1)785cm2;(2)15.7cm3
【分析】(1)根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算,即可求出圆柱的表面积。
(2)组合体的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】(1)3.14×10×20+3.14×(10÷2)2×2
=3.14×10×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(cm2)
圆柱的表面积是785cm2。
(2)3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×12×4+×3.14×12×3
=3.14×1×4+×3.14×1×3
=12.56+3.14
=15.7(cm3)
组合体的体积是15.7cm3。
15.43.96cm3
【分析】观察图形可知,该组合图形的体积=中间圆柱的体积+两边的两个圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(2÷2)2×(18-3×2)+×3.14×(2÷2)2×3×2
=3.14×12×(18-6)+×3.14×12×3×2
=3.14×12×12+×3.14×12×3×2
=3.14×1×12+×3.14×1×3×2
=37.68+6.28
=43.96(cm3)
16.2449.2立方厘米
【分析】根据圆柱的体积公式:V=πr2h,以及圆锥的体积公式:V=πr2h代入数据分别求出圆柱的体积和圆锥的体积,然后求出差,也就是剩下的体积。21教育网
【详解】3.14×(12÷2)2×25-3.14×(12÷2)2×10×
=3.14×62×25-3.14×62×10×
=3.14×36×25-3.14×36×10×
=2826-376.8
=2449.2(立方厘米)
剩下的体积是2449.2立方厘米。
17.60.56cm3
【分析】组合体是由一个长方体和一个圆锥组成,则组合体的体积=长方体的体积+圆锥的体积;
根据长方体的体积公式V=abh,圆锥的体积公式V=πr2h,代入数据计算即可求解。
【详解】长方体的体积:
4×4×3
=16×3
=48(cm3)
圆锥的体积:
×3.14×(4÷2)2×3
=×3.14×22×3
=×3.14×4×3
=12.56(cm3)
一共:48+12.56=60.56(cm3)
组合体的体积是60.56cm3。
18.7822.5立方厘米;6358.5立方厘米
【分析】观察第一个图形,是从一个长方体中截取了一个半圆柱,图形的体积=长方体的体积-半圆柱的体积,根据“V长方体=abh”“V圆柱=πr2h”,代入数据即可解答;
观察第二个图形可知:剩余部分的体积是圆柱与圆锥的体积之差,根据圆柱的体积:V=Sh,圆锥的体积公式:V=Sh,把数据分别代入公式解答即可。21世纪教育网版权所有
【详解】第一个图形的体积:
30×20×15-3.14×(10÷2)2×30÷2
=30×20×15-3.14×25×30÷2
=600×15-78.5×30÷2
=9000-2355÷2
=9000-1177.5
=7822.5(立方厘米)
它的体积是7822.5立方厘米。
第二个图形的体积:
3.14×()2×30-×3.14×()2×15
=3.14×92×30-×3.14×92×15
=3.14×81×30-×3.14×81×15
=3.14×81×30-3.14×81×5
=254.34×30-254.34×5
=7630.2-1271.7
=6358.5(立方厘米)
它的体积是6358.5立方厘米。
19.4286.1千克
【分析】分析题意可知:谷囤的体积=圆锥的体积+圆柱的体积,其中底面周长是6.28米,结合谷囤图形的特点可知:这个底面周长既是圆锥也是圆柱的底面周长,根据圆的周长=,则底面半径=底面周长÷()。圆锥的体积=,圆柱的体积=,代入数据分别计算出圆锥和圆柱的体积,进而求出谷囤的体积。又知每立方米稻谷约重650千克,则用谷囤的体积×650=这个谷囤的稻谷的总质量。据此解答即可。
【详解】6.28÷(2×3.14)
=6.28÷6.28
=1(米)
=
=
=6.28+0.314
=6.594(立方米)
6.594×650=4286.1(千克)
答:这个谷囤的稻谷约重4286.1千克。
20.471立方厘米
【分析】分析题目,陀螺是由一个圆柱体和一个圆锥体组成的,圆柱的体积=π(d÷2)2h,圆锥的体积=π(d÷2)2h,据此代入数据分别求出圆柱和圆锥的体积,再相加即可得到陀螺的体积。2·1·c·n·j·y
【详解】3.14×(10÷2)2×4
=3.14×52×4
=3.14×25×4
=78.5×4
=314(立方厘米)
3.14×(10÷2)2×6×
=3.14×52×6×
=3.14×25×6×
=78.5×6×
=471×
=157(立方厘米)
314+157=471(立方厘米)
答:这个陀螺的体积是471立方厘米。
21.50.24平方米;117立方米
【分析】根据题意得:蒙古包占地面积是圆柱底面积,圆柱底面直径为8米,则底面圆面积=;内部空间即为这个蒙古包的容积,蒙古包由一个圆锥和一个圆柱组成,则体积为两者之和,即,h1表示圆柱高度,h2表示圆锥高度,据此计算可得出答案。2-1-c-n-j-y
【详解】蒙古包占地面积为:
3.14×(8÷2)2
=3.14×42
=50.24(平方米)
内部空间大小为:
(立方米)
答:蒙古包所占的地面面积有50.24平方米;内部空间大约是117立方米。
22.5.652立方米
【分析】由图可知,新型储粮罐的体积=底面直径为2米,高0.9米的圆锥体积+底面直径为2米,高1.5米的圆锥体积+底面直径为2米,高1米的圆柱体积,根据圆柱的体积=πr2h,圆锥的体积=πr2h,代入数据解答即可。www-2-1-cnjy-com
【详解】2÷2=1(米)
3.14×12×0.9×+3.14×12×1+3.14×12×1.5×
=3.14×0.9×+3.14+3.14×1.5×
=2.826×+3.14+4.71×
=0.942+3.14+1.57
=4.082+1.57
=5.652(立方米)
答:新型储粮罐的体积是5.652立方米。
23.25.12÷2×3+25.12÷2×3×
【分析】如果把圆柱和圆锥重新分开,则表面积增加2个底面积,圆柱和圆锥的底面积相同,用25.12÷2即可求出每个底面积;然后根据圆柱的体积=底面积×高,圆锥的体积=底面积×高×,代入数据分别求出圆柱和圆锥的体积,再相加即可。21教育名师原创作品
【详解】25.12÷2×3+25.12÷2×3×
=37.68+12.56
=50.24(立方厘米)
答:原来这个物体的体积是50.24立方厘米。
24.30.144立方米
【分析】
粮囤的体积可以看作是一个圆柱的体积加上一个圆锥的体积,其中圆柱的底面积和圆锥的底面积相等,根据圆柱的体积=底面积×高,圆锥的体积=×底面积×高,代入相应数值计算,据此解答。
【详解】
底面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方米)
(立方米)
答:一个粮囤的体积是30.144立方米。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
