北师大数学八下第一章三角形的证明小测试(含解析)
文档属性
| 名称 | 北师大数学八下第一章三角形的证明小测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 21:05:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一章三角形的证明小测试
时间45分钟 满分120分
班级 姓名 编号
一.选择题(每小题8分,共48分)
1.如图,在△ABC中,∠ACB=90°,∠A=30°,CD是高,若BC=8,则AD的长为( )
1题图 2题图 3题图 4题图 5题图
A.16 B.12 C.10 D.8
2.如图,∠D=∠E=∠ACB=90°,能保证Rt△ADC≌Rt△CEB成立条件有( )
①∠ABC=45°;②AD=CE;③AC=2AD;④CD=BE.
A.1个 B.2个 C.3个 D.4个
3.如图,已知在△ABC中,DE垂直平分BC,若AB=5,△ABD的周长是13,则线段AC的长是( )
A.6 B.7 C.8 D.9
4.如图,已知△ABD是等边三角形,BC=DC,E在AD上,CE交BD于点F,AE=EC,若∠CBD=2∠DCE,则∠DCE的度数为( )
A.40° B.20° C.30° D.15°
5.如图,△ABC中,AD平分∠BAC,BD=AD=6,DF⊥AC于F,DF=4,则AB的长为( )
A.8 B.10 C. D.
6.如图,已知∠AOB=50°,点C,D分别在OA,OB上,OC=OD.进行如下操作:①分别以C,D为圆心,大于的长为半径画弧交于点P;②点E在OA上,以E为圆心,EO为半径画弧,交射线OP于点F,连接EF.则∠EFO的度数为( )
A.20° B.25° C.30° D.45°
二.填空题(每小题9分,共36分)
7.(2024秋 襄城县期末)如图,在△ABC和△DFE中,∠A=∠D=90°,AC=DE,若要用“斜边、直角边(HL)”直接证明Rt△ABC≌Rt△DFE,则还需补充条件: .
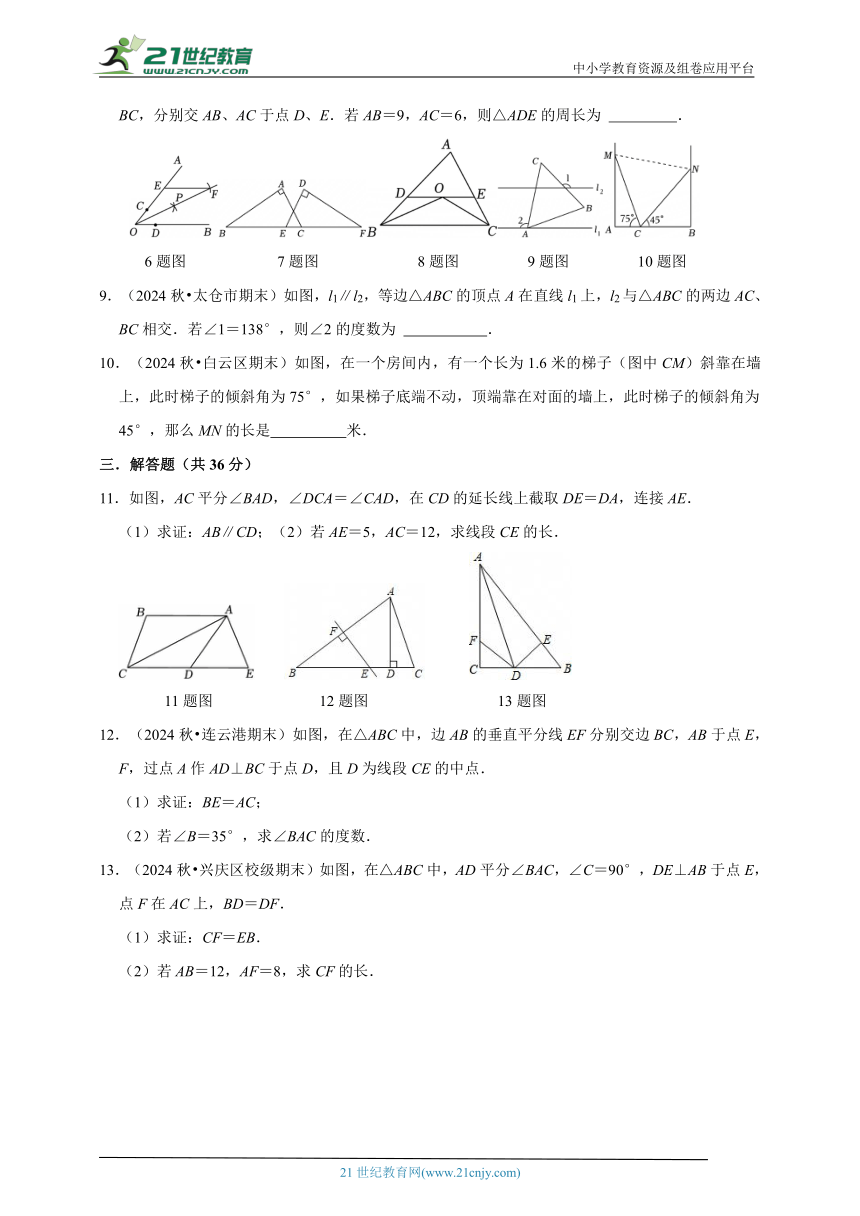
8.(2025 东台市开学)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=9,AC=6,则△ADE的周长为 .
6题图 7题图 8题图 9题图 10题图
9.(2024秋 太仓市期末)如图,l1∥l2,等边△ABC的顶点A在直线l1上,l2与△ABC的两边AC、BC相交.若∠1=138°,则∠2的度数为 .
10.(2024秋 白云区期末)如图,在一个房间内,有一个长为1.6米的梯子(图中CM)斜靠在墙上,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子的倾斜角为45°,那么MN的长是 米.
三.解答题(共36分)
11.如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)求证:AB∥CD;(2)若AE=5,AC=12,求线段CE的长.
11题图 12题图 13题图
12.(2024秋 连云港期末)如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC;
(2)若∠B=35°,求∠BAC的度数.
13.(2024秋 兴庆区校级期末)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
第一章三角形的证明小测试
参考答案与试题解析
一.选择题(每小题8分,共48分)
题号 1 2 3 4 5 6
答案 B C C B C B
1.(2024秋 天门期末)如图,在△ABC中,∠ACB=90°,∠A=30°,CD是高,若BC=8,则AD的长为( )
A.16 B.12 C.10 D.8
【答案】B
【解答】解:∵∠ACB=90°,∠A=30°,BC=8,
∴AB=2BC=16,∠B=60°,
又∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°﹣∠A=90°﹣30°=60°,
∴∠BCD=∠ACB﹣∠ACD=90°﹣60°=30°,
∴,
∴AD=AB﹣BD=12,
故选:B.
2.(2024秋 昭阳区期末)如图,∠D=∠E=∠ACB=90°,能保证Rt△ADC≌Rt△CEB成立条件有( )
①∠ABC=45°;
②AD=CE;
③AC=2AD;
④CD=BE.
A.1个 B.2个 C.3个 D.4个
【答案】C
【解答】解:根据三角形全等的判定条件“AAS、ASA”,
∴①∠ABC=45°,②AD=CE和④CD=BE满足定理“AAS和ASA”,
综上所述,正确的有①②和④,只有C选项正确,符合题意,
故选:C.
3.(2025 碑林区校级开学)如图,已知在△ABC中,DE垂直平分BC,若AB=5,△ABD的周长是13,则线段AC的长是( )
A.6 B.7 C.8 D.9
【答案】C
【解答】解:∵DE垂直平分BC,
∴DC=DB,
∴ABD的周长=AB+BD+AD=AB+CD+AD=AB+AC=13,
∵AB=5,
∴AC=8.
故选:C.
4.(2024秋 盐田区校级期末)如图,已知△ABD是等边三角形,BC=DC,E在AD上,CE交BD于点F,AE=EC,若∠CBD=2∠DCE,则∠DCE的度数为( )
A.40° B.20° C.30° D.15°
【答案】B
【解答】解:如图,连接AC,
由条件可知AB=AD,∠BAD=∠ADB=60°,
∵BC=CD,
∴∠CBD=∠CDB,AC垂直平分BD,
∴∠ACE∠BAD=30°,
∴∠ACE=∠EAC=30°,
∴∠DEF=∠ACE+∠EAC=60°,
∴△DEF为等边三角形,
∴∠DFE=60°,
∴∠CDB=2∠DCE,
∵∠CDF+∠DCE=∠DFE=60°,
∴2∠DCE+∠DCE=60°,
∴∠DCE=20°,
故选:B.
5.(2025 秦都区校级一模)如图,△ABC中,AD平分∠BAC,BD=AD=6,DF⊥AC于F,DF=4,则AB的长为( )
A.8 B.10 C. D.
【答案】C
【解答】解:如图所示,过点D作DE⊥AB于E,
∵AD平分∠BAC,DF⊥AC,DE⊥AB,
∴DE=DF=4,
∵BD=AD=6,
∴AB=2AE,
在Rt△ADE中,由勾股定理得,
∴,
故选:C.
6.(2024秋 遵义期末)如图,已知∠AOB=50°,点C,D分别在OA,OB上,OC=OD.进行如下操作:①分别以C,D为圆心,大于的长为半径画弧交于点P;②点E在OA上,以E为圆心,EO为半径画弧,交射线OP于点F,连接EF.则∠EFO的度数为( )
A.20° B.25° C.30° D.45°
【答案】B
【解答】解:由题意可知:OP平分∠AOB,∠AOB=50°,
∴,
∵EF=EO,
∴∠AOF=∠EFO=25°,
所以∠EFO的度数为25°,
故选:B.
二.填空题(每小题9分,共36分)
7.(2024秋 襄城县期末)如图,在△ABC和△DFE中,∠A=∠D=90°,AC=DE,若要用“斜边、直角边(HL)”直接证明Rt△ABC≌Rt△DFE,则还需补充条件: BC=FE .
【答案】BC=FE.
【解答】证明:在Rt△ABC和Rt△DFE中,
,
∴Rt△ABC≌Rt△DFE(HL).
故答案为:BC=FE.
8.(2025 东台市开学)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=9,AC=6,则△ADE的周长为 15 .
【答案】15.
【解答】解:由条件可知∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴BD=DO,CE=EO,
∴△ADE的周长为AD+DO+OE+AE=AD+BD+CE+AE=AB+AC=9+6=15,
故答案为:15.
9.(2024秋 太仓市期末)如图,l1∥l2,等边△ABC的顶点A在直线l1上,l2与△ABC的两边AC、BC相交.若∠1=138°,则∠2的度数为 102° .
【答案】102°.
【解答】解:如图所示:
∵∠1=138°,
∴∠3=180°﹣∠1=42°,
∵△ABC是等边三角形,
∴∠C=60°,
∴∠4=∠C+∠3=60°+42°=102°,
∵l1∥l2,
∴∠2=∠4=102°.
故答案为:102°.
10.(2024秋 白云区期末)如图,在一个房间内,有一个长为1.6米的梯子(图中CM)斜靠在墙上,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子的倾斜角为45°,那么MN的长是 1.6 米.
【答案】1.6.
【解答】解:有一个长为1.6米的梯子斜靠在墙上,倾斜角分别为75°,45°,
结合图形得:∠ACM=75°,∠BCN=45°,CM=1.6米,
∴∠MCN=180°﹣∠ACM﹣∠BCN=60°,
∵CM=CN,
∴△CMN为等边三角形,
∴MN=CM=1.6米,
故答案为:1.6.
三.解答题(共36分)
11.(2024秋 吉安县期末)如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)求证:AB∥CD;
(2)若AE=5,AC=12,求线段CE的长.
【解答】(1)证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠DCA=∠CAD,
∴∠BAC=∠ACD,
∴AB∥CD;
(2)解:∵DE=DA,
∴∠DAE=∠E,
∴,
∴∠CAE=90°,
∵AE=5,AC=12,
∴CE13.
12.(2024秋 连云港期末)如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC;
(2)若∠B=35°,求∠BAC的度数.
【解答】(1)证明:连接AE,
∵AD⊥BC于点D,且D为线段CE的中点,
∴AD垂直平分CE,
∴AC=AE,
∵EF垂直平分AB,
∴AE=BE,
∴BE=AC;
(2)解:∵AE=BE,∠B=35°,
∴∠BAE=∠B=35°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣35°=55°,
∴∠EAD=55°﹣35°=20°,
∵AC=AE,
∴∠AED=∠C,
∵∠AED+∠EAD=∠C+∠CAD=90°,
∴∠CAD=∠EAD=20°,
∴∠BAC=∠BAD+∠CAD=55°+20°=75°.
13.(2024秋 兴庆区校级期末)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
【解答】(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12﹣x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=12﹣x,
解得x=2,即CF=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第一章三角形的证明小测试
时间45分钟 满分120分
班级 姓名 编号
一.选择题(每小题8分,共48分)
1.如图,在△ABC中,∠ACB=90°,∠A=30°,CD是高,若BC=8,则AD的长为( )
1题图 2题图 3题图 4题图 5题图
A.16 B.12 C.10 D.8
2.如图,∠D=∠E=∠ACB=90°,能保证Rt△ADC≌Rt△CEB成立条件有( )
①∠ABC=45°;②AD=CE;③AC=2AD;④CD=BE.
A.1个 B.2个 C.3个 D.4个
3.如图,已知在△ABC中,DE垂直平分BC,若AB=5,△ABD的周长是13,则线段AC的长是( )
A.6 B.7 C.8 D.9
4.如图,已知△ABD是等边三角形,BC=DC,E在AD上,CE交BD于点F,AE=EC,若∠CBD=2∠DCE,则∠DCE的度数为( )
A.40° B.20° C.30° D.15°
5.如图,△ABC中,AD平分∠BAC,BD=AD=6,DF⊥AC于F,DF=4,则AB的长为( )
A.8 B.10 C. D.
6.如图,已知∠AOB=50°,点C,D分别在OA,OB上,OC=OD.进行如下操作:①分别以C,D为圆心,大于的长为半径画弧交于点P;②点E在OA上,以E为圆心,EO为半径画弧,交射线OP于点F,连接EF.则∠EFO的度数为( )
A.20° B.25° C.30° D.45°
二.填空题(每小题9分,共36分)
7.(2024秋 襄城县期末)如图,在△ABC和△DFE中,∠A=∠D=90°,AC=DE,若要用“斜边、直角边(HL)”直接证明Rt△ABC≌Rt△DFE,则还需补充条件: .
8.(2025 东台市开学)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=9,AC=6,则△ADE的周长为 .
6题图 7题图 8题图 9题图 10题图
9.(2024秋 太仓市期末)如图,l1∥l2,等边△ABC的顶点A在直线l1上,l2与△ABC的两边AC、BC相交.若∠1=138°,则∠2的度数为 .
10.(2024秋 白云区期末)如图,在一个房间内,有一个长为1.6米的梯子(图中CM)斜靠在墙上,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子的倾斜角为45°,那么MN的长是 米.
三.解答题(共36分)
11.如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)求证:AB∥CD;(2)若AE=5,AC=12,求线段CE的长.
11题图 12题图 13题图
12.(2024秋 连云港期末)如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC;
(2)若∠B=35°,求∠BAC的度数.
13.(2024秋 兴庆区校级期末)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
第一章三角形的证明小测试
参考答案与试题解析
一.选择题(每小题8分,共48分)
题号 1 2 3 4 5 6
答案 B C C B C B
1.(2024秋 天门期末)如图,在△ABC中,∠ACB=90°,∠A=30°,CD是高,若BC=8,则AD的长为( )
A.16 B.12 C.10 D.8
【答案】B
【解答】解:∵∠ACB=90°,∠A=30°,BC=8,
∴AB=2BC=16,∠B=60°,
又∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°﹣∠A=90°﹣30°=60°,
∴∠BCD=∠ACB﹣∠ACD=90°﹣60°=30°,
∴,
∴AD=AB﹣BD=12,
故选:B.
2.(2024秋 昭阳区期末)如图,∠D=∠E=∠ACB=90°,能保证Rt△ADC≌Rt△CEB成立条件有( )
①∠ABC=45°;
②AD=CE;
③AC=2AD;
④CD=BE.
A.1个 B.2个 C.3个 D.4个
【答案】C
【解答】解:根据三角形全等的判定条件“AAS、ASA”,
∴①∠ABC=45°,②AD=CE和④CD=BE满足定理“AAS和ASA”,
综上所述,正确的有①②和④,只有C选项正确,符合题意,
故选:C.
3.(2025 碑林区校级开学)如图,已知在△ABC中,DE垂直平分BC,若AB=5,△ABD的周长是13,则线段AC的长是( )
A.6 B.7 C.8 D.9
【答案】C
【解答】解:∵DE垂直平分BC,
∴DC=DB,
∴ABD的周长=AB+BD+AD=AB+CD+AD=AB+AC=13,
∵AB=5,
∴AC=8.
故选:C.
4.(2024秋 盐田区校级期末)如图,已知△ABD是等边三角形,BC=DC,E在AD上,CE交BD于点F,AE=EC,若∠CBD=2∠DCE,则∠DCE的度数为( )
A.40° B.20° C.30° D.15°
【答案】B
【解答】解:如图,连接AC,
由条件可知AB=AD,∠BAD=∠ADB=60°,
∵BC=CD,
∴∠CBD=∠CDB,AC垂直平分BD,
∴∠ACE∠BAD=30°,
∴∠ACE=∠EAC=30°,
∴∠DEF=∠ACE+∠EAC=60°,
∴△DEF为等边三角形,
∴∠DFE=60°,
∴∠CDB=2∠DCE,
∵∠CDF+∠DCE=∠DFE=60°,
∴2∠DCE+∠DCE=60°,
∴∠DCE=20°,
故选:B.
5.(2025 秦都区校级一模)如图,△ABC中,AD平分∠BAC,BD=AD=6,DF⊥AC于F,DF=4,则AB的长为( )
A.8 B.10 C. D.
【答案】C
【解答】解:如图所示,过点D作DE⊥AB于E,
∵AD平分∠BAC,DF⊥AC,DE⊥AB,
∴DE=DF=4,
∵BD=AD=6,
∴AB=2AE,
在Rt△ADE中,由勾股定理得,
∴,
故选:C.
6.(2024秋 遵义期末)如图,已知∠AOB=50°,点C,D分别在OA,OB上,OC=OD.进行如下操作:①分别以C,D为圆心,大于的长为半径画弧交于点P;②点E在OA上,以E为圆心,EO为半径画弧,交射线OP于点F,连接EF.则∠EFO的度数为( )
A.20° B.25° C.30° D.45°
【答案】B
【解答】解:由题意可知:OP平分∠AOB,∠AOB=50°,
∴,
∵EF=EO,
∴∠AOF=∠EFO=25°,
所以∠EFO的度数为25°,
故选:B.
二.填空题(每小题9分,共36分)
7.(2024秋 襄城县期末)如图,在△ABC和△DFE中,∠A=∠D=90°,AC=DE,若要用“斜边、直角边(HL)”直接证明Rt△ABC≌Rt△DFE,则还需补充条件: BC=FE .
【答案】BC=FE.
【解答】证明:在Rt△ABC和Rt△DFE中,
,
∴Rt△ABC≌Rt△DFE(HL).
故答案为:BC=FE.
8.(2025 东台市开学)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=9,AC=6,则△ADE的周长为 15 .
【答案】15.
【解答】解:由条件可知∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴BD=DO,CE=EO,
∴△ADE的周长为AD+DO+OE+AE=AD+BD+CE+AE=AB+AC=9+6=15,
故答案为:15.
9.(2024秋 太仓市期末)如图,l1∥l2,等边△ABC的顶点A在直线l1上,l2与△ABC的两边AC、BC相交.若∠1=138°,则∠2的度数为 102° .
【答案】102°.
【解答】解:如图所示:
∵∠1=138°,
∴∠3=180°﹣∠1=42°,
∵△ABC是等边三角形,
∴∠C=60°,
∴∠4=∠C+∠3=60°+42°=102°,
∵l1∥l2,
∴∠2=∠4=102°.
故答案为:102°.
10.(2024秋 白云区期末)如图,在一个房间内,有一个长为1.6米的梯子(图中CM)斜靠在墙上,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子的倾斜角为45°,那么MN的长是 1.6 米.
【答案】1.6.
【解答】解:有一个长为1.6米的梯子斜靠在墙上,倾斜角分别为75°,45°,
结合图形得:∠ACM=75°,∠BCN=45°,CM=1.6米,
∴∠MCN=180°﹣∠ACM﹣∠BCN=60°,
∵CM=CN,
∴△CMN为等边三角形,
∴MN=CM=1.6米,
故答案为:1.6.
三.解答题(共36分)
11.(2024秋 吉安县期末)如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)求证:AB∥CD;
(2)若AE=5,AC=12,求线段CE的长.
【解答】(1)证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠DCA=∠CAD,
∴∠BAC=∠ACD,
∴AB∥CD;
(2)解:∵DE=DA,
∴∠DAE=∠E,
∴,
∴∠CAE=90°,
∵AE=5,AC=12,
∴CE13.
12.(2024秋 连云港期末)如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC;
(2)若∠B=35°,求∠BAC的度数.
【解答】(1)证明:连接AE,
∵AD⊥BC于点D,且D为线段CE的中点,
∴AD垂直平分CE,
∴AC=AE,
∵EF垂直平分AB,
∴AE=BE,
∴BE=AC;
(2)解:∵AE=BE,∠B=35°,
∴∠BAE=∠B=35°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣35°=55°,
∴∠EAD=55°﹣35°=20°,
∵AC=AE,
∴∠AED=∠C,
∵∠AED+∠EAD=∠C+∠CAD=90°,
∴∠CAD=∠EAD=20°,
∴∠BAC=∠BAD+∠CAD=55°+20°=75°.
13.(2024秋 兴庆区校级期末)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
【解答】(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12﹣x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=12﹣x,
解得x=2,即CF=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
