模型16 “倍长中线”模型 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型16 “倍长中线”模型 (含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 328.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 22:53:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
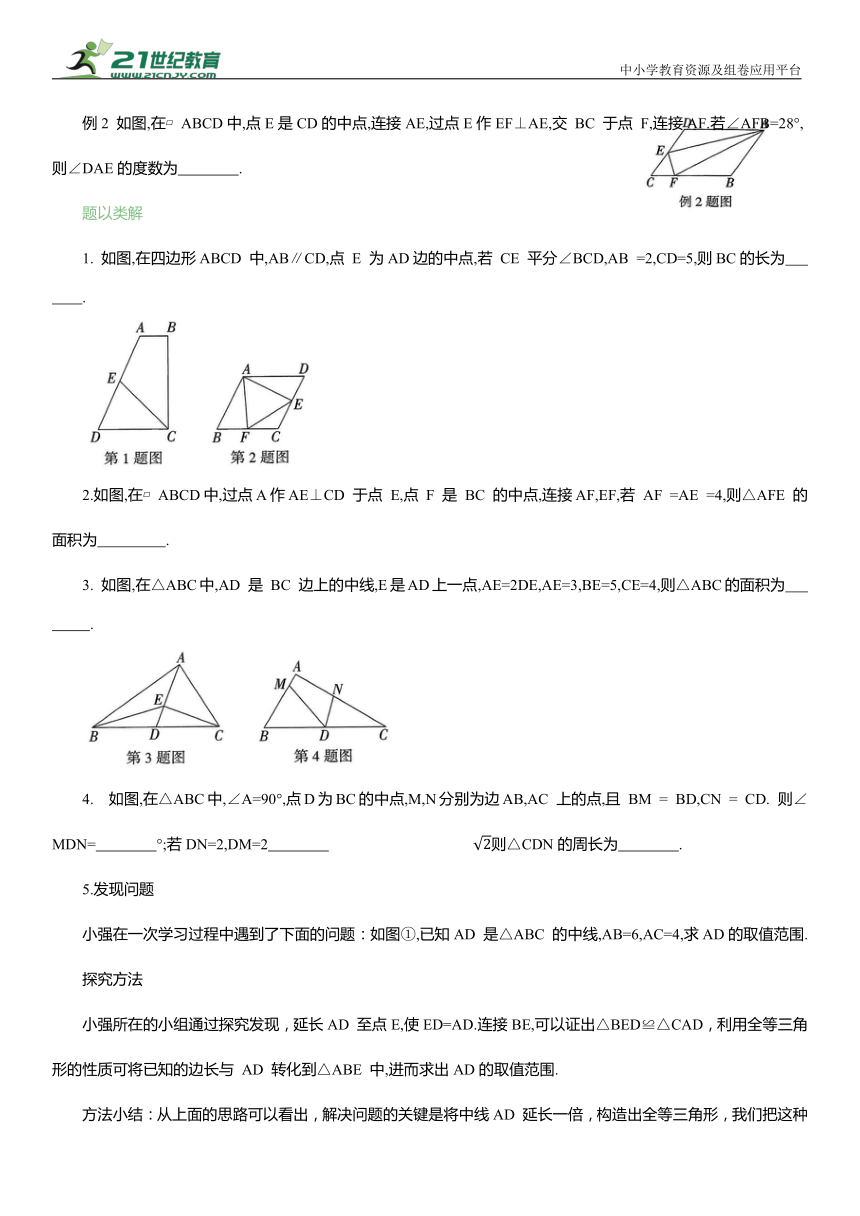
模型16 “倍长中线”模型
基础模型
类型 倍长中线
图示
条件 AD是△ABC的边BC上的中线
结论 延长AD至点E,使DE=AD,连接BE,则△ACD≌△EBD
结论分析
结论:△ACD≌△EBD
证明:∵AD 是△ABC的边 BC上的中线,∴CD=BD,
又∵AD=ED,∠ADC=∠EDB,∴△ACD≌△EBD(SAS).
模型拓展
类型 倍长类中线
图示
条件 点D是 BC边的中点,点E是AB上一点,连接ED
结论 延长 ED至点 F,使DF=ED,连接CF,则△BDE≌△CDF
模型解题三步法
例1 如图,在△ABC中,∠BAC=135°,AD为BC边上的中线,且AD⊥AC,AC=2,则△ABC的面积为 .
例2 如图,在 ABCD中,点E是CD的中点,连接AE,过点E作EF⊥AE,交 BC 于点 F,连接AF.若∠AFB=28°,则∠DAE的度数为 .
题以类解
1. 如图,在四边形ABCD 中,AB∥CD,点 E 为AD边的中点,若 CE 平分∠BCD,AB =2,CD=5,则BC的长为 .
2.如图,在 ABCD中,过点A作AE⊥CD 于点 E,点 F 是 BC 的中点,连接AF,EF,若 AF =AE =4,则△AFE 的面积为 .
3. 如图,在△ABC中,AD 是 BC 边上的中线,E是AD上一点,AE=2DE,AE=3,BE=5,CE=4,则△ABC的面积为 .
4. 如图,在△ABC中,∠A=90°,点D为BC的中点,M,N分别为边AB,AC 上的点,且 BM = BD,CN = CD. 则∠MDN= °;若DN=2,DM=2 则△CDN的周长为 .
5.发现问题
小强在一次学习过程中遇到了下面的问题:如图①,已知AD 是△ABC 的中线,AB=6,AC=4,求AD的取值范围.
探究方法
小强所在的小组通过探究发现,延长AD 至点E,使ED=AD.连接BE,可以证出△BED≌△CAD,利用全等三角形的性质可将已知的边长与 AD 转化到△ABE 中,进而求出AD的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线AD 延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
(1)请你利用上面解答问题的思路方法,写出求AD的取值范围的过程;
类比迁移
(2)如图②,AD 是△ABC 的中线,在 AD 上取一点 E,连接BE 并延长交AC 于点 F,使AF=EF,求证:BE=AC;
拓展应用
(3)如图③,在矩形ABCD中, 在 BD上取一点 F,以 BF 为斜边作 Rt△BEF,且 点G是DF的中点,连接EG,CG.
求证:EG=CG.
模型解题三步法
例1 2 【解析】根据“倍长中线”模型得△ADC≌△EDB(SAS),∴BE=AC=2,∠E=∠DAC=90°,∵ ∠BAE=∠BAC--∠DAC=45°,∴AE=BE=2,∴S△ABC=S△ABE= ×2x2=2.
例2 E CD EF
14° 【解析】在 ABCD 中,AD∥BC,∴∠MDE=∠FCE,∠EMD=∠EFC,又∵ E是 CD 的中点,∴ DE = CE,∴ △EDM≌△ECF(AAS),∴ EM=EF,又∵ EF⊥AE,∴AF=AM,即△AMF 是等腰三角形,∴AE平分∠DAF.∵ AD∥BC,∴∠DAF=∠AFB=
题以类解
1.7 【解析】找模型:是否存在四边形一边上的中点:E 为AD 的中点;是否存在一顶点与中点的连线:线段 CE.抽离模型:如解图,延长 CE到点 P,使CE=PE,连接AP,用模型:根据“倍长中线”模型得△AEP≌△DEC(SAS),∴ AP=CD,∠P=∠ECD,∴AP∥CD,∵AB∥CD,∴点 P,A,B在同一直线上.∵CE 平分∠BCD,∴ ∠BCP=∠DCP,∴∠BCP=∠P,∴BC=BP,∴AB+AP=AB+CD=BP=7=BC.
2. 4 一题多解
解法一:找模型:是否存在三角形一边上的中点:F为BC 的中点;是否存在三角形一顶点与中点的连线:线段AF;抽离模型:如解图①,用模型:延长AF至点G,使得FG=AF,连接CG,根据“倍长中线”模型得△ABF≌△GCF,∴ ∠B = ∠BCG. ∵ ∠B +∠BCD =180°,∴∠BCG+∠BCD=180°,∴E,C,G三点共线.∵AE⊥CD,点 F是AG的中点,∴AF=EF.又∵AF=AE,∴△AEF 是等边三角形(三条边相等的三角形是等边三角形),
解法二:找模型:是否存在三角形一边上的中点:F为BC 的中点;是否存在某条边上的中点与另外两条边中的任意一条边上某点(不在端点)的连线:线段 EF;抽离模型:如解图②,用模型:过点 B 作 BH∥DC 交 EF 的延长线于点H,∵AB∥CD,∴A,B,H三点共线.根据“倍长中线”模型得△CFE≌△BFH(AAS),∴HF=EF,∵AE⊥DC,AB∥DC,∴∠BAE=∠AED=90°,∵点 F 是 EH 的中点,AF=EF.又∵ AF=AE,∴△AEF 是等边三角形(三条边相等的三角形是等边三角形),
3. 18 【解析】如解图,延长AD 到点 F,使ED=DF,连接CF,根据“倍长中线”模型得△BDE≌△CDF(SAS),∴ CF=BE=5,∵ AE=2DE,
4. 45,2 【解析】如解图,延长MD至点E,使DE=MD,连接CE,NE,过点 N作 NF⊥MD 于点 F.∵ ∠A=90°,∴ ∠BCA+∠B =90°,∵ BM = BD, CN = CD,∴ ∠BMD =∠BDM,∠CDN=∠CND,∴2∠BDM+∠B=180°,2∠CDN+∠BCA =180°,∴ 2∠BDM+2∠CDN=270°,∴ ∠CDN+∠BDM = 135°,∴ ∠MDN=180°-(∠CDN+∠BDM)= 45°;在 Rt△NDF 中,∵ ∠FDN = 45°, DN = 2, 在△DBM 和△DCE 中,
,∴CE=BM=BD=CD=CN,∠ECD =∠B,又∵ ∠B+∠BCA =90°,∴ ∠ECN=∠ECD+∠BCA=90°,∴△ECN是等腰直角三角形, (等腰直角三角形的性质),在 Rt△NFE中, EF 的周长=2CN+
5. (1)解:如解图①,延长 AD 至点 E,使 DE=AD,连接BE,根据“倍长中线”模型得△CAD≌△BED(SAS),
∴AC=BE=4,
在△ABE中,AB-BE∴2<2AD<10,
∴1(2)证明:如解图②,延长AD 至点 H,使DH=AD,连接BH,
根据“倍长中线”模型得△ADC≌△HDB(SAS),
∴AC=HB,∠CAD=∠H.
∵AF=EF,
∴∠FAE=∠AEF,
∴∠H=∠BEH,
∴BE=BH,
∴BE=AC;
(3)证明:如解图③,延长 CG 至点N,使NG=CG,连接EN,NF,EC,
根据“倍长中线”模型得△CGD≌△NGF(SAS),∴CD=NF,∠CDB=∠NFG.
∴∠ADB=∠EBF.
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠EBF=∠DBC,
∴∠EBC=2∠DBC.
∵ ∠EBF+∠EFB = 90°,∠DBC+∠BDC =90°,
∴∠EFB=∠BDC=∠NFG,∠EBF+∠EFB+∠DBC+∠BDC=180°,
∴2∠DBC+∠EFB+∠NFG=180°,
又∵∠NFG+∠BFE+∠EFN=180°,
∴∠EFN=2∠DBC,∴∠EBC=∠EFN.
且CD=NF,
∴△BEC∽△FEN,
∴∠BEC=∠FEN,
∴∠BEF=∠NEC=90°.
又∵CG=NG,
模型16 “倍长中线”模型
基础模型
类型 倍长中线
图示
条件 AD是△ABC的边BC上的中线
结论 延长AD至点E,使DE=AD,连接BE,则△ACD≌△EBD
结论分析
结论:△ACD≌△EBD
证明:∵AD 是△ABC的边 BC上的中线,∴CD=BD,
又∵AD=ED,∠ADC=∠EDB,∴△ACD≌△EBD(SAS).
模型拓展
类型 倍长类中线
图示
条件 点D是 BC边的中点,点E是AB上一点,连接ED
结论 延长 ED至点 F,使DF=ED,连接CF,则△BDE≌△CDF
模型解题三步法
例1 如图,在△ABC中,∠BAC=135°,AD为BC边上的中线,且AD⊥AC,AC=2,则△ABC的面积为 .
例2 如图,在 ABCD中,点E是CD的中点,连接AE,过点E作EF⊥AE,交 BC 于点 F,连接AF.若∠AFB=28°,则∠DAE的度数为 .
题以类解
1. 如图,在四边形ABCD 中,AB∥CD,点 E 为AD边的中点,若 CE 平分∠BCD,AB =2,CD=5,则BC的长为 .
2.如图,在 ABCD中,过点A作AE⊥CD 于点 E,点 F 是 BC 的中点,连接AF,EF,若 AF =AE =4,则△AFE 的面积为 .
3. 如图,在△ABC中,AD 是 BC 边上的中线,E是AD上一点,AE=2DE,AE=3,BE=5,CE=4,则△ABC的面积为 .
4. 如图,在△ABC中,∠A=90°,点D为BC的中点,M,N分别为边AB,AC 上的点,且 BM = BD,CN = CD. 则∠MDN= °;若DN=2,DM=2 则△CDN的周长为 .
5.发现问题
小强在一次学习过程中遇到了下面的问题:如图①,已知AD 是△ABC 的中线,AB=6,AC=4,求AD的取值范围.
探究方法
小强所在的小组通过探究发现,延长AD 至点E,使ED=AD.连接BE,可以证出△BED≌△CAD,利用全等三角形的性质可将已知的边长与 AD 转化到△ABE 中,进而求出AD的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线AD 延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
(1)请你利用上面解答问题的思路方法,写出求AD的取值范围的过程;
类比迁移
(2)如图②,AD 是△ABC 的中线,在 AD 上取一点 E,连接BE 并延长交AC 于点 F,使AF=EF,求证:BE=AC;
拓展应用
(3)如图③,在矩形ABCD中, 在 BD上取一点 F,以 BF 为斜边作 Rt△BEF,且 点G是DF的中点,连接EG,CG.
求证:EG=CG.
模型解题三步法
例1 2 【解析】根据“倍长中线”模型得△ADC≌△EDB(SAS),∴BE=AC=2,∠E=∠DAC=90°,∵ ∠BAE=∠BAC--∠DAC=45°,∴AE=BE=2,∴S△ABC=S△ABE= ×2x2=2.
例2 E CD EF
14° 【解析】在 ABCD 中,AD∥BC,∴∠MDE=∠FCE,∠EMD=∠EFC,又∵ E是 CD 的中点,∴ DE = CE,∴ △EDM≌△ECF(AAS),∴ EM=EF,又∵ EF⊥AE,∴AF=AM,即△AMF 是等腰三角形,∴AE平分∠DAF.∵ AD∥BC,∴∠DAF=∠AFB=
题以类解
1.7 【解析】找模型:是否存在四边形一边上的中点:E 为AD 的中点;是否存在一顶点与中点的连线:线段 CE.抽离模型:如解图,延长 CE到点 P,使CE=PE,连接AP,用模型:根据“倍长中线”模型得△AEP≌△DEC(SAS),∴ AP=CD,∠P=∠ECD,∴AP∥CD,∵AB∥CD,∴点 P,A,B在同一直线上.∵CE 平分∠BCD,∴ ∠BCP=∠DCP,∴∠BCP=∠P,∴BC=BP,∴AB+AP=AB+CD=BP=7=BC.
2. 4 一题多解
解法一:找模型:是否存在三角形一边上的中点:F为BC 的中点;是否存在三角形一顶点与中点的连线:线段AF;抽离模型:如解图①,用模型:延长AF至点G,使得FG=AF,连接CG,根据“倍长中线”模型得△ABF≌△GCF,∴ ∠B = ∠BCG. ∵ ∠B +∠BCD =180°,∴∠BCG+∠BCD=180°,∴E,C,G三点共线.∵AE⊥CD,点 F是AG的中点,∴AF=EF.又∵AF=AE,∴△AEF 是等边三角形(三条边相等的三角形是等边三角形),
解法二:找模型:是否存在三角形一边上的中点:F为BC 的中点;是否存在某条边上的中点与另外两条边中的任意一条边上某点(不在端点)的连线:线段 EF;抽离模型:如解图②,用模型:过点 B 作 BH∥DC 交 EF 的延长线于点H,∵AB∥CD,∴A,B,H三点共线.根据“倍长中线”模型得△CFE≌△BFH(AAS),∴HF=EF,∵AE⊥DC,AB∥DC,∴∠BAE=∠AED=90°,∵点 F 是 EH 的中点,AF=EF.又∵ AF=AE,∴△AEF 是等边三角形(三条边相等的三角形是等边三角形),
3. 18 【解析】如解图,延长AD 到点 F,使ED=DF,连接CF,根据“倍长中线”模型得△BDE≌△CDF(SAS),∴ CF=BE=5,∵ AE=2DE,
4. 45,2 【解析】如解图,延长MD至点E,使DE=MD,连接CE,NE,过点 N作 NF⊥MD 于点 F.∵ ∠A=90°,∴ ∠BCA+∠B =90°,∵ BM = BD, CN = CD,∴ ∠BMD =∠BDM,∠CDN=∠CND,∴2∠BDM+∠B=180°,2∠CDN+∠BCA =180°,∴ 2∠BDM+2∠CDN=270°,∴ ∠CDN+∠BDM = 135°,∴ ∠MDN=180°-(∠CDN+∠BDM)= 45°;在 Rt△NDF 中,∵ ∠FDN = 45°, DN = 2, 在△DBM 和△DCE 中,
,∴CE=BM=BD=CD=CN,∠ECD =∠B,又∵ ∠B+∠BCA =90°,∴ ∠ECN=∠ECD+∠BCA=90°,∴△ECN是等腰直角三角形, (等腰直角三角形的性质),在 Rt△NFE中, EF 的周长=2CN+
5. (1)解:如解图①,延长 AD 至点 E,使 DE=AD,连接BE,根据“倍长中线”模型得△CAD≌△BED(SAS),
∴AC=BE=4,
在△ABE中,AB-BE
∴1
根据“倍长中线”模型得△ADC≌△HDB(SAS),
∴AC=HB,∠CAD=∠H.
∵AF=EF,
∴∠FAE=∠AEF,
∴∠H=∠BEH,
∴BE=BH,
∴BE=AC;
(3)证明:如解图③,延长 CG 至点N,使NG=CG,连接EN,NF,EC,
根据“倍长中线”模型得△CGD≌△NGF(SAS),∴CD=NF,∠CDB=∠NFG.
∴∠ADB=∠EBF.
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠EBF=∠DBC,
∴∠EBC=2∠DBC.
∵ ∠EBF+∠EFB = 90°,∠DBC+∠BDC =90°,
∴∠EFB=∠BDC=∠NFG,∠EBF+∠EFB+∠DBC+∠BDC=180°,
∴2∠DBC+∠EFB+∠NFG=180°,
又∵∠NFG+∠BFE+∠EFN=180°,
∴∠EFN=2∠DBC,∴∠EBC=∠EFN.
且CD=NF,
∴△BEC∽△FEN,
∴∠BEC=∠FEN,
∴∠BEF=∠NEC=90°.
又∵CG=NG,
同课章节目录
