模型8 “双角平分线”模型 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型8 “双角平分线”模型 (含答案)2025年中考数学几何模型专题复习 |

|
|
| 格式 | docx | ||
| 文件大小 | 196.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 22:50:20 | ||
图片预览

文档简介
模型8 “双角平分线”模型
基础模型
类型 双内角平分线型 双外角平分线型 一内一外平分线型
图示
条件 在△ABC 中,BD,CD分别是∠ABC,∠ACB的平分线 在△ABC中,BD,CD分别是∠EBC,∠FCB的平分线 在 △ABC 中, BD,CD 分别是∠ABC,∠ACE的平分线
结论 ∠D=90°+ ∠A ∠D=90°- ∠A ∠D= ∠A
结论分析
双内角平分线型结论:
证明:∵BD平分∠ABC,CD平分∠ACB,
双外角平分线型结论:
自主证明:
自主证明:
模型拓展
拓展方向:三等分角的情况下,角之间的数量关系
类型 双内角三等分线型 双外角三等分线型 一内一外三等分线型
图示
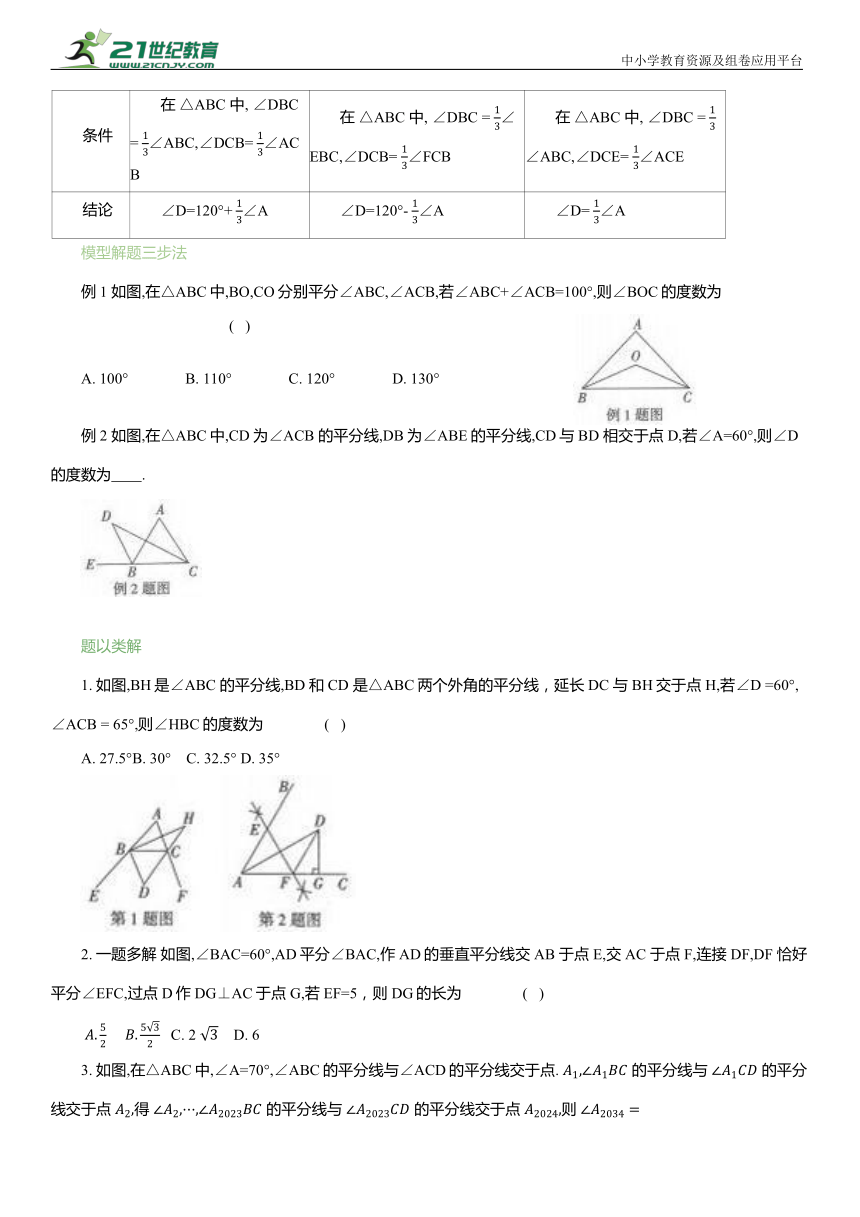
条件 在 △ABC 中, ∠DBC = ∠ABC,∠DCB= ∠ACB 在 △ABC 中, ∠DBC = ∠EBC,∠DCB= ∠FCB 在 △ABC 中, ∠DBC = ∠ABC,∠DCE= ∠ACE
结论 ∠D=120°+ ∠A ∠D=120°- ∠A ∠D= ∠A
模型解题三步法
例1 如图,在△ABC中,BO,CO分别平分∠ABC,∠ACB,若∠ABC+∠ACB=100°,则∠BOC的度数为 ( )
A. 100° B. 110° C. 120° D. 130°
例2 如图,在△ABC中,CD为∠ACB 的平分线,DB为∠ABE的平分线,CD与BD 相交于点D,若∠A=60°,则∠D 的度数为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,BH是∠ABC 的平分线,BD 和CD 是△ABC两个外角的平分线,延长DC 与 BH交于点 H,若∠D =60°,∠ACB = 65°,则∠HBC的度数为 ( )
A. 27.5°B. 30° C. 32.5° D. 35°
2. 一题多解 如图,∠BAC=60°,AD平分∠BAC,作AD的垂直平分线交 AB 于点 E,交 AC 于点 F,连接 DF,DF 恰好平分∠EFC,过点D作DG⊥AC于点 G,若EF=5,则DG的长为 ( )
C. 2 D. 6
3. 如图,在△ABC中,∠A=70°,∠ABC的平分线与∠ACD的平分线交于点. 的平分线与 的平分线交于点 得 的平分线与 的平分线交于点 则
4. 如图,在△ABC中, 若∠AED=35°,则∠C 的度数为 .
如图,在△ABC中,∠A=120°,BD,CD 分别平分∠ABC,∠ACB,则∠BDC= ,若BG,CG分别是∠ABC,∠ACB的外角平分线,则∠G=
模型展现
双外角平分线型 自主证明:
∵BD平分∠EBC,CD平分∠FCB,
初高教辅站 ∴ ∠D =180°-(∠DBC+∠DCB)
一内一外平分线型 自主证明:
∵BD平分∠ABC,CD平分∠ACE,
∵∠DCE=∠D+∠DBC,∠ACE=∠A+∠ABC,
模型解题三步法
例1 D 【解析】∵ ∠ABC+∠ACB = 100°,∴∠A=80°,∵ BO,CO 分别平分∠ABC,∠ACB,根据“双内角平分线”模型可得:
例2 CD BD CD BD
30° 【解析】∵ CD 平分∠ACB,DB 平分∠ABE,∠A =60°,根据“一内一外角平分线”模型可得:
题以类解
1. A 【解析】找模型:是否存在两条角平分线:BD平分 ∠CBE, CD 平分∠BCF.是内角平分线还是外角平分线:两条角平分线均为外角平分线.抽离模型:如解图,用模型:根据“双外角平分线”模型可得:∠D=90°- ∠A,∵∠D=60°,∴∠A=60°,∵ ∠ACB=65°,∴ ∠ABC=180°-60°-65°=55°,∵ BH 是∠ABC 的平分线,∴ ∠HBC=
2. B 一题多解
解法一:找模型:是否存在两条角平分线:AD 平分 ∠BAC, FD 平 分∠EFG.是内角平分线还是外角平分线:AD 是内角平分线,FD 是外角平分线.抽离模型:如解图,用模型:设AD 与EF 交于点 H. ∵ ∠BAC = 60°, AD 平分 ∵ EF 垂直平分 AD,∴ ∠AHE = 90°,∴ ∠AEF = 60°,∴△AEF为等边三角形,∴ FD=AF=EF=5,根据“一内一外双角平分线”模型可得
解法二:∵EF⊥AD,AD 平分∠EAC,∴△EHA≌△FHA(ASA),∴ EH=HF,在 Rt△AEH 中, ∵ DF 平分∠HFG,DG⊥FG,∴ DG=DH =
【解析】∵∠A=70°,BA ,CA 分别平分∠ABC,∠ACD,∴∠A = ∠A=35°(“一内一外角平分线”模型),同理可得, 由此可得, 教辅资料小考教辅站初高教辅
4. 75° 【解析】∵∠AED=35°,∴∠AEB=180°- (“双内角三等分线”模型),即 解得∠C=75°.
5. 150°,30° 【解析】在△ABC中,∵BD,CD 分别平分 (“双内角平分线”模型). ∵ BG,CG 分别是∠ABC,∠ACB 的外角平分线,∴ ∠GBC+∠GCB= 150°=30°(“双外角平分线”模型).
基础模型
类型 双内角平分线型 双外角平分线型 一内一外平分线型
图示
条件 在△ABC 中,BD,CD分别是∠ABC,∠ACB的平分线 在△ABC中,BD,CD分别是∠EBC,∠FCB的平分线 在 △ABC 中, BD,CD 分别是∠ABC,∠ACE的平分线
结论 ∠D=90°+ ∠A ∠D=90°- ∠A ∠D= ∠A
结论分析
双内角平分线型结论:
证明:∵BD平分∠ABC,CD平分∠ACB,
双外角平分线型结论:
自主证明:
自主证明:
模型拓展
拓展方向:三等分角的情况下,角之间的数量关系
类型 双内角三等分线型 双外角三等分线型 一内一外三等分线型
图示
条件 在 △ABC 中, ∠DBC = ∠ABC,∠DCB= ∠ACB 在 △ABC 中, ∠DBC = ∠EBC,∠DCB= ∠FCB 在 △ABC 中, ∠DBC = ∠ABC,∠DCE= ∠ACE
结论 ∠D=120°+ ∠A ∠D=120°- ∠A ∠D= ∠A
模型解题三步法
例1 如图,在△ABC中,BO,CO分别平分∠ABC,∠ACB,若∠ABC+∠ACB=100°,则∠BOC的度数为 ( )
A. 100° B. 110° C. 120° D. 130°
例2 如图,在△ABC中,CD为∠ACB 的平分线,DB为∠ABE的平分线,CD与BD 相交于点D,若∠A=60°,则∠D 的度数为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,BH是∠ABC 的平分线,BD 和CD 是△ABC两个外角的平分线,延长DC 与 BH交于点 H,若∠D =60°,∠ACB = 65°,则∠HBC的度数为 ( )
A. 27.5°B. 30° C. 32.5° D. 35°
2. 一题多解 如图,∠BAC=60°,AD平分∠BAC,作AD的垂直平分线交 AB 于点 E,交 AC 于点 F,连接 DF,DF 恰好平分∠EFC,过点D作DG⊥AC于点 G,若EF=5,则DG的长为 ( )
C. 2 D. 6
3. 如图,在△ABC中,∠A=70°,∠ABC的平分线与∠ACD的平分线交于点. 的平分线与 的平分线交于点 得 的平分线与 的平分线交于点 则
4. 如图,在△ABC中, 若∠AED=35°,则∠C 的度数为 .
如图,在△ABC中,∠A=120°,BD,CD 分别平分∠ABC,∠ACB,则∠BDC= ,若BG,CG分别是∠ABC,∠ACB的外角平分线,则∠G=
模型展现
双外角平分线型 自主证明:
∵BD平分∠EBC,CD平分∠FCB,
初高教辅站 ∴ ∠D =180°-(∠DBC+∠DCB)
一内一外平分线型 自主证明:
∵BD平分∠ABC,CD平分∠ACE,
∵∠DCE=∠D+∠DBC,∠ACE=∠A+∠ABC,
模型解题三步法
例1 D 【解析】∵ ∠ABC+∠ACB = 100°,∴∠A=80°,∵ BO,CO 分别平分∠ABC,∠ACB,根据“双内角平分线”模型可得:
例2 CD BD CD BD
30° 【解析】∵ CD 平分∠ACB,DB 平分∠ABE,∠A =60°,根据“一内一外角平分线”模型可得:
题以类解
1. A 【解析】找模型:是否存在两条角平分线:BD平分 ∠CBE, CD 平分∠BCF.是内角平分线还是外角平分线:两条角平分线均为外角平分线.抽离模型:如解图,用模型:根据“双外角平分线”模型可得:∠D=90°- ∠A,∵∠D=60°,∴∠A=60°,∵ ∠ACB=65°,∴ ∠ABC=180°-60°-65°=55°,∵ BH 是∠ABC 的平分线,∴ ∠HBC=
2. B 一题多解
解法一:找模型:是否存在两条角平分线:AD 平分 ∠BAC, FD 平 分∠EFG.是内角平分线还是外角平分线:AD 是内角平分线,FD 是外角平分线.抽离模型:如解图,用模型:设AD 与EF 交于点 H. ∵ ∠BAC = 60°, AD 平分 ∵ EF 垂直平分 AD,∴ ∠AHE = 90°,∴ ∠AEF = 60°,∴△AEF为等边三角形,∴ FD=AF=EF=5,根据“一内一外双角平分线”模型可得
解法二:∵EF⊥AD,AD 平分∠EAC,∴△EHA≌△FHA(ASA),∴ EH=HF,在 Rt△AEH 中, ∵ DF 平分∠HFG,DG⊥FG,∴ DG=DH =
【解析】∵∠A=70°,BA ,CA 分别平分∠ABC,∠ACD,∴∠A = ∠A=35°(“一内一外角平分线”模型),同理可得, 由此可得, 教辅资料小考教辅站初高教辅
4. 75° 【解析】∵∠AED=35°,∴∠AEB=180°- (“双内角三等分线”模型),即 解得∠C=75°.
5. 150°,30° 【解析】在△ABC中,∵BD,CD 分别平分 (“双内角平分线”模型). ∵ BG,CG 分别是∠ABC,∠ACB 的外角平分线,∴ ∠GBC+∠GCB= 150°=30°(“双外角平分线”模型).
同课章节目录
