模型9 “高+角平分线”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型9 “高+角平分线”模型(含答案)2025年中考数学几何模型专题复习 | 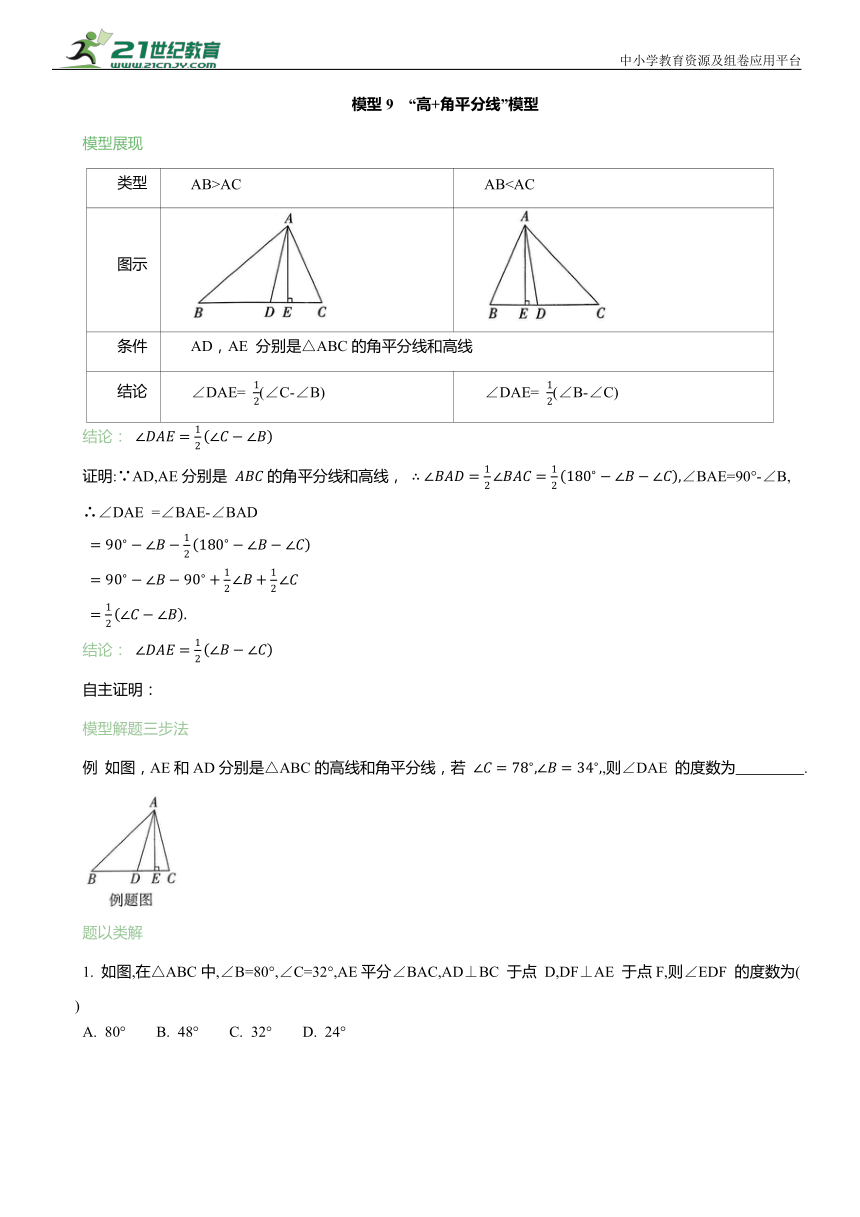 | |
| 格式 | docx | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 21:06:44 | ||
图片预览


文档简介
模型9 “高+角平分线”模型
模型展现
类型 AB>AC AB图示
条件 AD,AE 分别是△ABC的角平分线和高线
结论 ∠DAE= (∠C-∠B) ∠DAE= (∠B-∠C)
中小学教育资源及组卷应用平台
结论:
证明:∵AD,AE分别是 的角平分线和高线, ∠BAE=90°-∠B,
∴∠DAE =∠BAE-∠BAD
结论:
自主证明:
模型解题三步法
例 如图,AE和AD分别是△ABC的高线和角平分线,若 ,则∠DAE 的度数为 .
题以类解
1. 如图,在△ABC中,∠B=80°,∠C=32°,AE平分∠BAC,AD⊥BC 于点 D,DF⊥AE 于点F,则∠EDF 的度数为( )
A. 80° B. 48° C. 32° D. 24°
2. 如图,在△ABC中,AD 是 BC边上的高,AE,BF分别是∠BAC,∠ABC 的平分线,AD 与BF交于点 H,AE 与 BF 交于点 G,已知∠AGB=125°,∠ABC =60°,则∠EAD 的度数为 .
3. 在 中,AB≠AC,AD,AE分别是 的高和角平分线,若 则∠ACB的度数为 .
4. 如图①,在△ABC中,AE平分∠BAC,AD⊥BC.
(1)若 .求∠DAE 的度数;
(2)如图②,若把“AD⊥BC”变成“点 F 在AE的延长线上,且 FD⊥BC”,设∠BAC=α, ,请用α,β的代数式表示 的度数.
模型展现
自主证明:
∵AD,AE 分别是△ABC 的角平分线和高线,
∠CAE=90°-∠C,
∴ ∠DAE = ∠CAE - ∠CAD = 90°-∠C -
模型解题三步法
例 22° 【解析】找模型:是否存在三角形中的角平分线:角平分线AD,是否存在与角平分线共顶点的高线:高线AE.抽离模型:如解图,用模型:根据“高+角平分线”模型可得:∠DAE=
题以类解
1. D 【解析】找模型:是否存在三角形中的角平分线:角平分线AE;是否存在与角平分线共顶点的高线:高线AD.抽离模型:如解图,用模型:根据“高+角平分线”模型可得: DF⊥AE,∴∠EDF+∠DEF=∠DEF+∠DAE,∴∠EDF=∠DAE=24°.
2.5° 【解析】找模型:是否存在三角形中的角平分线:角平分线AE.是否存在与角平分线共顶点的高线:高线AD.抽离模型:如解图,∵ ∠AGB = 125°,∴ ∠GAB +∠GBA =180°-125°=55°.∵AE,BF分别是∠BAC,∠ABC 的 平 分线,∴ ∠BAC + ∠ABC =2(∠GAB+∠GBA)= 110°,∴ ∠C=70°. 用模型:根据“高+角平分线”模型可得:
3. 30°或70° 【解析】如解图①,当ABAC时, (“高+角平分线”模型),∵ ∠B = 50°,∠DAE = 10°,
4. 解:(1)∵AE平分∠BAC,AD⊥BC,
∴∠DAE=∠DAC-∠EAC=90°-∠C-∠EAC= (“高+角平分线”模型);
(2)如解图,过点A作AG⊥BC于点 G,则∠AGC=90°.
又∵FD⊥BC,
∴∠FDB=90°,
:. AG∥DF,
∴∠DFE=∠GAE.
∵∠GAE=∠GAC-∠CAE= (“高+角平分线”模型),
模型展现
类型 AB>AC AB
条件 AD,AE 分别是△ABC的角平分线和高线
结论 ∠DAE= (∠C-∠B) ∠DAE= (∠B-∠C)
中小学教育资源及组卷应用平台
结论:
证明:∵AD,AE分别是 的角平分线和高线, ∠BAE=90°-∠B,
∴∠DAE =∠BAE-∠BAD
结论:
自主证明:
模型解题三步法
例 如图,AE和AD分别是△ABC的高线和角平分线,若 ,则∠DAE 的度数为 .
题以类解
1. 如图,在△ABC中,∠B=80°,∠C=32°,AE平分∠BAC,AD⊥BC 于点 D,DF⊥AE 于点F,则∠EDF 的度数为( )
A. 80° B. 48° C. 32° D. 24°
2. 如图,在△ABC中,AD 是 BC边上的高,AE,BF分别是∠BAC,∠ABC 的平分线,AD 与BF交于点 H,AE 与 BF 交于点 G,已知∠AGB=125°,∠ABC =60°,则∠EAD 的度数为 .
3. 在 中,AB≠AC,AD,AE分别是 的高和角平分线,若 则∠ACB的度数为 .
4. 如图①,在△ABC中,AE平分∠BAC,AD⊥BC.
(1)若 .求∠DAE 的度数;
(2)如图②,若把“AD⊥BC”变成“点 F 在AE的延长线上,且 FD⊥BC”,设∠BAC=α, ,请用α,β的代数式表示 的度数.
模型展现
自主证明:
∵AD,AE 分别是△ABC 的角平分线和高线,
∠CAE=90°-∠C,
∴ ∠DAE = ∠CAE - ∠CAD = 90°-∠C -
模型解题三步法
例 22° 【解析】找模型:是否存在三角形中的角平分线:角平分线AD,是否存在与角平分线共顶点的高线:高线AE.抽离模型:如解图,用模型:根据“高+角平分线”模型可得:∠DAE=
题以类解
1. D 【解析】找模型:是否存在三角形中的角平分线:角平分线AE;是否存在与角平分线共顶点的高线:高线AD.抽离模型:如解图,用模型:根据“高+角平分线”模型可得: DF⊥AE,∴∠EDF+∠DEF=∠DEF+∠DAE,∴∠EDF=∠DAE=24°.
2.5° 【解析】找模型:是否存在三角形中的角平分线:角平分线AE.是否存在与角平分线共顶点的高线:高线AD.抽离模型:如解图,∵ ∠AGB = 125°,∴ ∠GAB +∠GBA =180°-125°=55°.∵AE,BF分别是∠BAC,∠ABC 的 平 分线,∴ ∠BAC + ∠ABC =2(∠GAB+∠GBA)= 110°,∴ ∠C=70°. 用模型:根据“高+角平分线”模型可得:
3. 30°或70° 【解析】如解图①,当AB
4. 解:(1)∵AE平分∠BAC,AD⊥BC,
∴∠DAE=∠DAC-∠EAC=90°-∠C-∠EAC= (“高+角平分线”模型);
(2)如解图,过点A作AG⊥BC于点 G,则∠AGC=90°.
又∵FD⊥BC,
∴∠FDB=90°,
:. AG∥DF,
∴∠DFE=∠GAE.
∵∠GAE=∠GAC-∠CAE= (“高+角平分线”模型),
同课章节目录
