模型11 “等分面积”模型 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型11 “等分面积”模型 (含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 250.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 21:07:12 | ||
图片预览

文档简介
模型11 “等分面积”模型
基础模型
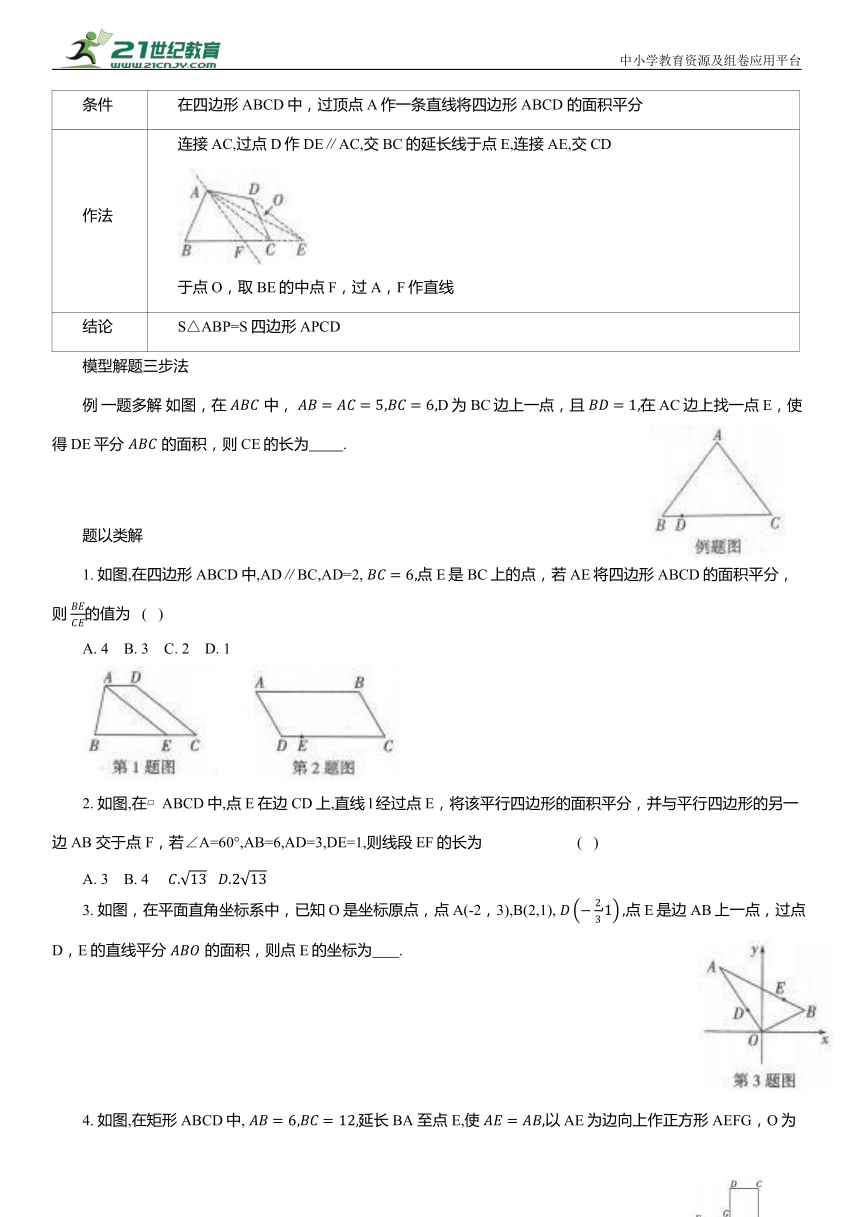
图示
条件 在△ABC中,过边BC 上一点 D 作一条直线将三角形面积平分
作法 作法一:取BC的中点E,连接AE, AD,过点 E作EF∥AD交AC于点 F,过D,F两点作直线,交AE于点O 作法二:连接AD,过点 B 作BE∥AD,交 CA 延长线于点 E,连接ED,交AB于点 O,取 CE 的中点F,过D,F两点作直线
结论 1. S△AEF=S△EPD; 2. S△AOF=S△pog; 3. S△OPC=S四边形ABDF 1. S△ABD=S△AED; 2. S△AOE=S△DOB; 3. S△DPC=S四边形ABDF
作法一结论: F
证明: (结论1),
结论2).
∵点E是BC的中点,
3即 (结论3).
作法二结论:1
自主证明:
模型拓展
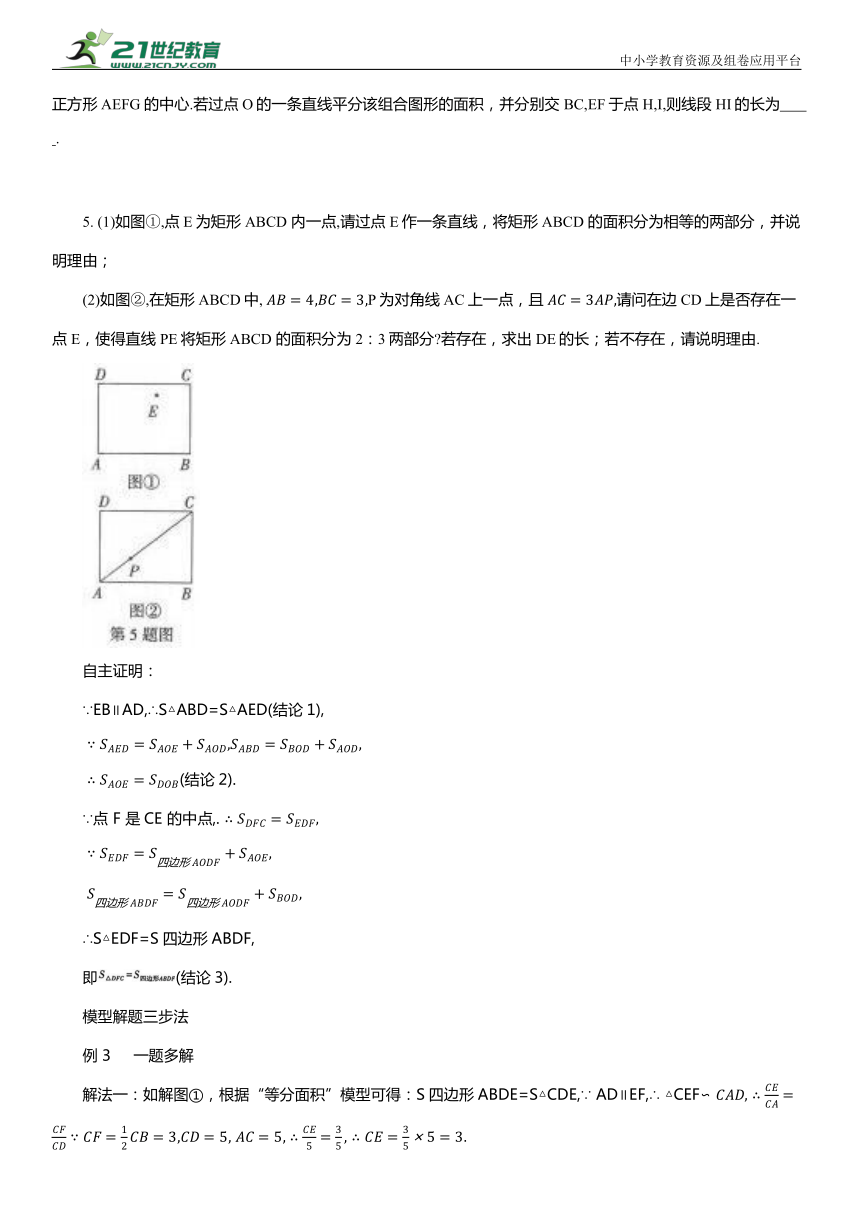
图示
条件 在四边形ABCD中,过顶点A作一条直线将四边形ABCD 的面积平分
作法 连接AC,过点D作DE∥AC,交BC的延长线于点E,连接AE,交CD 于点O,取BE的中点F,过A,F作直线
结论 S△ABP=S四边形APCD
模型解题三步法
例 一题多解 如图,在 中, D为BC边上一点,且 在AC边上找一点E,使得DE平分 的面积,则CE的长为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,在四边形ABCD中,AD∥BC,AD=2, 点E是BC上的点,若AE将四边形ABCD的面积平分,则 的值为 ( )
A. 4 B. 3 C. 2 D. 1
2. 如图,在 ABCD中,点E在边 CD上,直线l经过点E,将该平行四边形的面积平分,并与平行四边形的另一边 AB 交于点 F,若∠A=60°,AB=6,AD=3,DE=1,则线段EF的长为 ( )
A. 3 B. 4
3. 如图,在平面直角坐标系中,已知O是坐标原点,点A(-2,3),B(2,1), 点E是边AB上一点,过点D,E的直线平分 的面积,则点 E的坐标为 .
4. 如图,在矩形ABCD中, 延长BA 至点 E,使 以AE为边向上作正方形AEFG,O为正方形AEFG的中心.若过点O的一条直线平分该组合图形的面积,并分别交 BC,EF于点 H,I,则线段HI的长为 .
5. (1)如图①,点E为矩形ABCD 内一点,请过点E作一条直线,将矩形ABCD 的面积分为相等的两部分,并说明理由;
(2)如图②,在矩形ABCD中, P为对角线AC上一点,且 请问在边CD上是否存在一点 E,使得直线 PE将矩形ABCD 的面积分为2:3两部分 若存在,求出DE的长;若不存在,请说明理由.
自主证明:
∵EB∥AD,∴S△ABD=S△AED(结论1),
(结论2).
∵点 F 是CE 的中点,.
∴S△EDF=S四边形ABDF,
即(结论3).
模型解题三步法
例 3 一题多解
解法一:如解图①,根据“等分面积”模型可得:S四边形ABDE=S△CDE,∵ AD∥EF,∴ △CEF∽
解法二:找模型:是否存在三角形:△ABC,在三角形的边上是否存在一点且过该点所在的直线平分三角形的面积:BC 边上的点 D,抽离模型:如解图②,用模型:根据“等分面积”模型可得:S四边形ABDE = S△CDE, ∵ AD ∥BF,
题以类解
1. C 【解析】找模型:是否存在四边形:四边形ABCD;在四边形的边上是否存在一点且过该点所在的直线平分四边形的面积:BC 边上的点E.抽离模型:如解图,用模型:过点A 作AF⊥BC于点 F, 根据“等分面积”模型得: 解得BE=4,∴ CE=
2. C 【解析】找模型:是否存在四边形:四边形ABCD,在四边形的边上是否存在一点且过该点所在的直线平分四边形的面积:CD 边上的点E;抽离模型:如解图,用模型:分别过点D 和点 E 作 DG⊥AB,EH⊥AB 于点 G 和H,∴四边形 DGHE 为矩形,∴GH=DE=1,∵在□ABCD中,AD=3,∠A=60°,∴AG= 根据“等分面积”模型得:EF平分平行四边形面积,∴EF 经过平行四边形对角线交点,∴DE=BF=1,∴FH=AB-AG 在 Rt△EHF 中,根据勾 股定理,得
【解析】∵A(-2,3),∴ 直线 OA 的解析式为 令 得y=1,∴点D 在 OA 上.设直线AB 的解析式为y= kx+b,把A(-2,3),B(2,1)代入,得 令x=0,得y=2,设 AB 与 y轴的交点为 C,∴ C(0,2),∴点 C 为AB 的中点,如解图,连接CD,过点 O 作 OE∥CD,交AB 于点 E,连接 DE,S△ADE=S四边形EDOB(“等分面积”模型),则DE平分△ABO 的面积,∵CD∥OE,∴△ACD 解得 设点E的坐标为 则有 解得a=1或 ∵CD∥OE,∴点E的坐标为(
4. 6 【解析】如解图,连接AC,BD 交于点 J,过点O 作OK⊥EB于点 K,过点 J作 JL⊥EB于点L,过点O 作OM⊥JL 于点 M.∵点 J 和点O 分别为矩形ABCD 和正方形AEFG的中心,∴直线 IH 平分该组合图形的面积(“等分面积”模型),∵ JL∥BC,且点 J 为AC 的中点 同理可得 ∵OK⊥AE,ML⊥AB,OM⊥JL,∴四边形OKLM 为矩形,∴ML=OK=3,∴ JM=JL-ML=6-3=3,在 Rt△OMJ中,
5. 解:(1)如解图①,连接AC,BD 交于点 O,过点 E,O 作直线,直线 EO 将矩形ABCD 的面积分为相等的两部分.
理由:设直线 EO分别交 DC,AB 于点 M,N,
∵四边形ABCD 是矩形,
∴AB∥CD,OA=OC,
∴ ∠MCO=∠NAO,
在△MCO 和△NAO中,
∴ △MCO≌△NAO(ASA),∴S△MCO=S△NAO,易得
(2)存在.
如解图②,作 MN∥BC,使得 S矩形ABCD,连接AM,DN 交于点 O,作直线OP 交 CD 于点 E,交 AB 于点 H,此时
形ABCD,
∵AB∥CD,∴∠EMO=∠HAO,在△EOM 和△HOA 中,
∴△EOM≌△HOA(ASA),
∴AH=EM,设AH=EM=x,
解得 即
基础模型
图示
条件 在△ABC中,过边BC 上一点 D 作一条直线将三角形面积平分
作法 作法一:取BC的中点E,连接AE, AD,过点 E作EF∥AD交AC于点 F,过D,F两点作直线,交AE于点O 作法二:连接AD,过点 B 作BE∥AD,交 CA 延长线于点 E,连接ED,交AB于点 O,取 CE 的中点F,过D,F两点作直线
结论 1. S△AEF=S△EPD; 2. S△AOF=S△pog; 3. S△OPC=S四边形ABDF 1. S△ABD=S△AED; 2. S△AOE=S△DOB; 3. S△DPC=S四边形ABDF
作法一结论: F
证明: (结论1),
结论2).
∵点E是BC的中点,
3即 (结论3).
作法二结论:1
自主证明:
模型拓展
图示
条件 在四边形ABCD中,过顶点A作一条直线将四边形ABCD 的面积平分
作法 连接AC,过点D作DE∥AC,交BC的延长线于点E,连接AE,交CD 于点O,取BE的中点F,过A,F作直线
结论 S△ABP=S四边形APCD
模型解题三步法
例 一题多解 如图,在 中, D为BC边上一点,且 在AC边上找一点E,使得DE平分 的面积,则CE的长为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,在四边形ABCD中,AD∥BC,AD=2, 点E是BC上的点,若AE将四边形ABCD的面积平分,则 的值为 ( )
A. 4 B. 3 C. 2 D. 1
2. 如图,在 ABCD中,点E在边 CD上,直线l经过点E,将该平行四边形的面积平分,并与平行四边形的另一边 AB 交于点 F,若∠A=60°,AB=6,AD=3,DE=1,则线段EF的长为 ( )
A. 3 B. 4
3. 如图,在平面直角坐标系中,已知O是坐标原点,点A(-2,3),B(2,1), 点E是边AB上一点,过点D,E的直线平分 的面积,则点 E的坐标为 .
4. 如图,在矩形ABCD中, 延长BA 至点 E,使 以AE为边向上作正方形AEFG,O为正方形AEFG的中心.若过点O的一条直线平分该组合图形的面积,并分别交 BC,EF于点 H,I,则线段HI的长为 .
5. (1)如图①,点E为矩形ABCD 内一点,请过点E作一条直线,将矩形ABCD 的面积分为相等的两部分,并说明理由;
(2)如图②,在矩形ABCD中, P为对角线AC上一点,且 请问在边CD上是否存在一点 E,使得直线 PE将矩形ABCD 的面积分为2:3两部分 若存在,求出DE的长;若不存在,请说明理由.
自主证明:
∵EB∥AD,∴S△ABD=S△AED(结论1),
(结论2).
∵点 F 是CE 的中点,.
∴S△EDF=S四边形ABDF,
即(结论3).
模型解题三步法
例 3 一题多解
解法一:如解图①,根据“等分面积”模型可得:S四边形ABDE=S△CDE,∵ AD∥EF,∴ △CEF∽
解法二:找模型:是否存在三角形:△ABC,在三角形的边上是否存在一点且过该点所在的直线平分三角形的面积:BC 边上的点 D,抽离模型:如解图②,用模型:根据“等分面积”模型可得:S四边形ABDE = S△CDE, ∵ AD ∥BF,
题以类解
1. C 【解析】找模型:是否存在四边形:四边形ABCD;在四边形的边上是否存在一点且过该点所在的直线平分四边形的面积:BC 边上的点E.抽离模型:如解图,用模型:过点A 作AF⊥BC于点 F, 根据“等分面积”模型得: 解得BE=4,∴ CE=
2. C 【解析】找模型:是否存在四边形:四边形ABCD,在四边形的边上是否存在一点且过该点所在的直线平分四边形的面积:CD 边上的点E;抽离模型:如解图,用模型:分别过点D 和点 E 作 DG⊥AB,EH⊥AB 于点 G 和H,∴四边形 DGHE 为矩形,∴GH=DE=1,∵在□ABCD中,AD=3,∠A=60°,∴AG= 根据“等分面积”模型得:EF平分平行四边形面积,∴EF 经过平行四边形对角线交点,∴DE=BF=1,∴FH=AB-AG 在 Rt△EHF 中,根据勾 股定理,得
【解析】∵A(-2,3),∴ 直线 OA 的解析式为 令 得y=1,∴点D 在 OA 上.设直线AB 的解析式为y= kx+b,把A(-2,3),B(2,1)代入,得 令x=0,得y=2,设 AB 与 y轴的交点为 C,∴ C(0,2),∴点 C 为AB 的中点,如解图,连接CD,过点 O 作 OE∥CD,交AB 于点 E,连接 DE,S△ADE=S四边形EDOB(“等分面积”模型),则DE平分△ABO 的面积,∵CD∥OE,∴△ACD 解得 设点E的坐标为 则有 解得a=1或 ∵CD∥OE,∴点E的坐标为(
4. 6 【解析】如解图,连接AC,BD 交于点 J,过点O 作OK⊥EB于点 K,过点 J作 JL⊥EB于点L,过点O 作OM⊥JL 于点 M.∵点 J 和点O 分别为矩形ABCD 和正方形AEFG的中心,∴直线 IH 平分该组合图形的面积(“等分面积”模型),∵ JL∥BC,且点 J 为AC 的中点 同理可得 ∵OK⊥AE,ML⊥AB,OM⊥JL,∴四边形OKLM 为矩形,∴ML=OK=3,∴ JM=JL-ML=6-3=3,在 Rt△OMJ中,
5. 解:(1)如解图①,连接AC,BD 交于点 O,过点 E,O 作直线,直线 EO 将矩形ABCD 的面积分为相等的两部分.
理由:设直线 EO分别交 DC,AB 于点 M,N,
∵四边形ABCD 是矩形,
∴AB∥CD,OA=OC,
∴ ∠MCO=∠NAO,
在△MCO 和△NAO中,
∴ △MCO≌△NAO(ASA),∴S△MCO=S△NAO,易得
(2)存在.
如解图②,作 MN∥BC,使得 S矩形ABCD,连接AM,DN 交于点 O,作直线OP 交 CD 于点 E,交 AB 于点 H,此时
形ABCD,
∵AB∥CD,∴∠EMO=∠HAO,在△EOM 和△HOA 中,
∴△EOM≌△HOA(ASA),
∴AH=EM,设AH=EM=x,
解得 即
同课章节目录
