第一章动量守恒定律综合提升--高中物理选择性必修一素养提升学案
文档属性
| 名称 | 第一章动量守恒定律综合提升--高中物理选择性必修一素养提升学案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-03-12 14:01:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
高中物理选择性必修一素养提升学案
第一章 动量守恒定律
综合提升
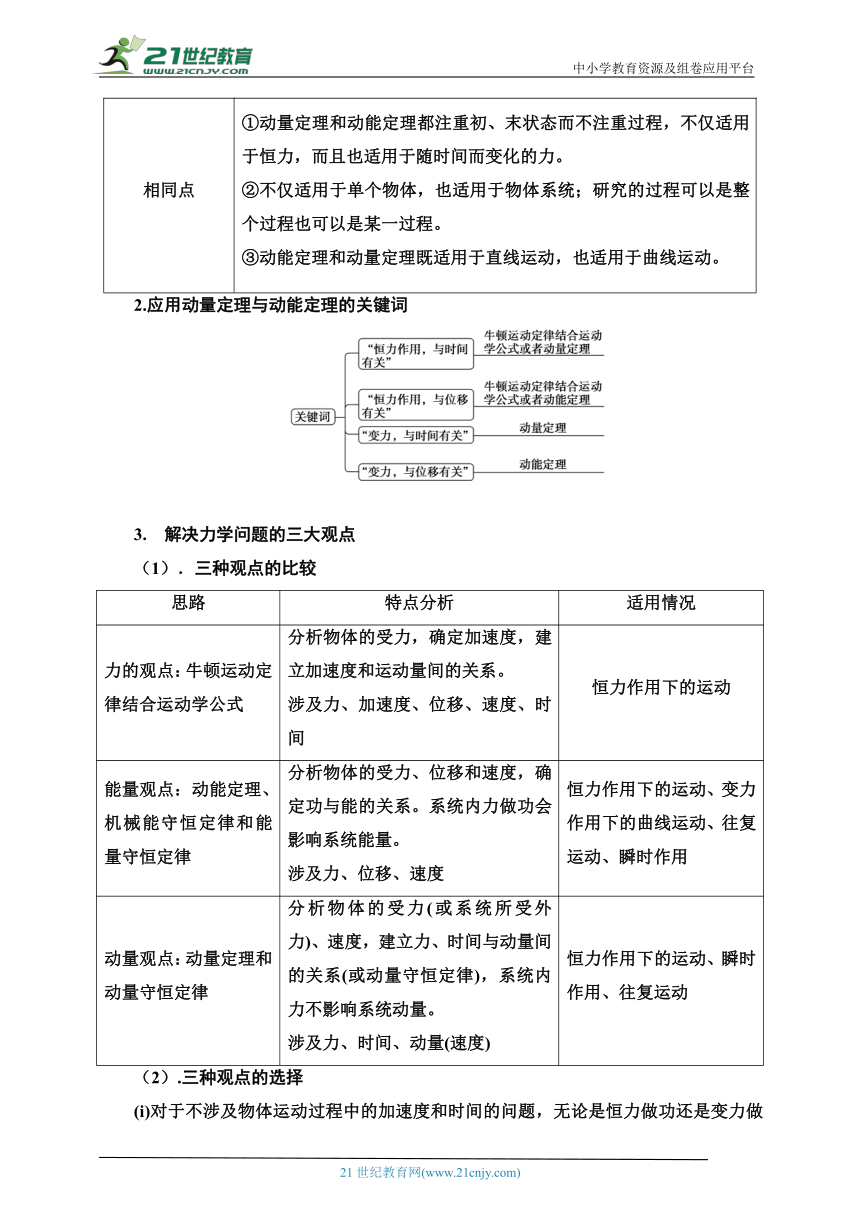
【知识点图解】
【方法探究】
1.动量定理和动能定理的比较:
动量定理 动能定理
内容 物体所受合外力的冲量等于物体的动量变化量 物体所受合外力的功等于物体动能的变化量
公式 F合t=mv2-mv1 F合s=mv-mv
矢标性 矢量式 标量式
因果关系 因 合外力的冲量 合外力的功(总功)
果 动量的变化 动能的变化
相同点 ①动量定理和动能定理都注重初、末状态而不注重过程,不仅适用于恒力,而且也适用于随时间而变化的力。②不仅适用于单个物体,也适用于物体系统;研究的过程可以是整个过程也可以是某一过程。③动能定理和动量定理既适用于直线运动,也适用于曲线运动。
2.应用动量定理与动能定理的关键词
3. 解决力学问题的三大观点
(1).三种观点的比较
思路 特点分析 适用情况
力的观点:牛顿运动定律结合运动学公式 分析物体的受力,确定加速度,建立加速度和运动量间的关系。涉及力、加速度、位移、速度、时间 恒力作用下的运动
能量观点:动能定理、机械能守恒定律和能量守恒定律 分析物体的受力、位移和速度,确定功与能的关系。系统内力做功会影响系统能量。涉及力、位移、速度 恒力作用下的运动、变力作用下的曲线运动、往复运动、瞬时作用
动量观点:动量定理和动量守恒定律 分析物体的受力(或系统所受外力)、速度,建立力、时间与动量间的关系(或动量守恒定律),系统内力不影响系统动量。涉及力、时间、动量(速度) 恒力作用下的运动、瞬时作用、往复运动
(2).三种观点的选择
(i)对于不涉及物体运动过程中的加速度和时间的问题,无论是恒力做功还是变力做功,一般都利用动能定理求解;如果只有重力和弹簧弹力做功而不涉及运动过程的加速度和时间问题,则采用机械能守恒定律求解。
(ii)对于碰撞、反冲类问题,应用动量守恒定律求解;对于相互作用的两物体,若明确两物体相对滑动的距离,应考虑选用能量守恒(功能关系)建立方程。
4.综合应用动力学“三大观点”解题的步骤:
1 认真审题,明确题目所述的物理情景,确定研究对象.
2 分析所选研究对象的受力情况及运动状态和运动状态的变化过程。对于过程复杂的问题,要正确、合理地把全过程分成若干阶段,注意分析各阶段之间的联系
3 根据各阶段状态变化的规律确定解题方法,选择合理的规律列方程,有时还要分析题目的隐含条件、临界条件、几何关系等列出辅助方程.
4 代入数据 统一单位 ,计算结果,必要时要对结果进行讨论.
【题型探究】
一、动量定理
【典例1】 (2020·甘肃张掖高台一中高二下月考节选)如图所示,质量mA=4.0 kg的木板A放在水平面C上,木板与水平面间的动摩擦因数μ=0.24,木板右端放着质量mB=1.0 kg的小物块B(可视为质点),它们均处于静止状态。木板突然受到水平向右的12 N·s的瞬时冲量作用开始运动,当小物块滑离木板时,木板的动能EkA=8.0 J,小物块的动能EkB=0.5 J,重力加速度g取10 m/s2,求:
(1)瞬时冲量作用结束时木板的速度大小v0;
(2)木板的长度L。
[解析] (1)在瞬时冲量作用时,木板A受水平面和小物块B的摩擦力的冲量均可以忽略。
取水平向右为正方向,对木板A,由动量定理有I=mAv0,代入数据解得v0=3 m/s。
(2)设A对B、B对A、C对A的滑动摩擦力大小分别为FfAB、FfBA、FfCA,B在A上滑行的时间为t,B离开A时A的速度为vA,B的速度为vB,A、B相对C的位移为sA、sB。
对A,由动量定理有-(FfBA+FfCA)t=mAvA-mAv0,
对B,由动量定理有FfABt=mBvB,
由牛顿第三定律可得FfBA=FfAB,另FfCA=μ(mA+mB)g,
对A,由动能定理有-(FfBA+FfCA)sA=mAv-mAv,
对B,由动能定理有FfABsB=mBv,
根据动量与动能之间的关系有mAvA=,
mBvB=,
木板A的长度即B相对A滑动距离的大小,故L=sA-sB,
联立解得L=0.5 m。
[答案] (1)3 m/s (2)0.5 m
[一语通关] 1 动量定理和动能定理都是求解力学问题的重要定理。应用时要特别注意选定研究对象和过程,注重受力情况分析和运动情况分析,灵活运用规律求解。
2 运用动量定理解题需考虑速度的方向,运用动能定理解题则不需考虑速度的方向。
二、碰撞
【典例2】 如图所示,质量分别为mA、mB的两个弹性小球A、B静止在地面上方,B球距地面的高度h=0.8 m,A球在B球的正上方。先将B球释放,经过一段时间后再将A球释放。当A球下落t=0.3 s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰好为零。已知mB=3mA,重力加速度大小g取10 m/s2,忽略空气阻力及碰撞中的动能损失。求:
(1)B球第一次到达地面时的速度;
(2)P点距离地面的高度。
[解析] (1)设B球第一次到达地面时的速度大小为vB,由运动学公式有vB=,
将h=0.8 m代入上式,得vB=4 m/s。
(2)设两球相碰前后,A球的速度大小分别为v1和v1′(v1′=0),B球的速度分别为v2和v2′,
由运动学规律可得v1=gt,
由于碰撞时间极短,重力的作用可以忽略,两球相碰前后的动量守恒,总动能保持不变。规定竖直向下的方向为正方向,有mAv1+mBv2=mBv2′,
mAv+mBv=mBv2′2,
设B球与地面相碰后的速度大小为vB′,忽略碰撞中的动能损失可得vB′=vB,
设P点距地面的高度为h′,由运动学规律可得
h′=,
联立各式,并代入已知条件可得
h′=0.75 m。
[答案] (1)4 m/s (2)0.75 m
三、反冲
【典例3】反冲小车静止放在水平光滑玻璃上,点燃酒精,蒸汽将橡皮塞水平喷出,小车沿相反方向运动。如果小车运动前的总质量M=3 kg,水平喷出的橡皮塞的质量m=0.1 kg。
(1)若橡皮塞喷出时获得的水平速度v=2.9 m/s,求小车的反冲速度;
(2)若橡皮塞喷出时速度大小不变,方向与水平方向成60°角,小车的反冲速度又如何(小车一直在水平方向运动)
[解析] (1)以橡皮塞运动的方向为正方向,根据动量守恒定律有
mv+(M-m)v′=0
v′=-v=-×2.9 m/s=-0.1 m/s
负号表示小车的运动方向与橡皮塞运动的方向相反。
(2)以橡皮塞运动的水平分运动方向为正方向,有
mvcos 60°+(M-m)v″=0
v″=-=- m/s=-0.05 m/s
负号表示小车的运动方向与橡皮塞运动的水平分运动的方向相反。
[答案] (1)0.1 m/s,方向与橡皮塞运动的方向相反
(2)0.05 m/s,方向与橡皮塞运动的水平分运动的方向相反
四、滑块木板模型
【典例4】.(16分)(2023北京昌平模拟)如图所示,光滑水平地面上固定一竖直挡板P,质量mB=2kg的木板B静止在水平面上,木板右端与挡板P的距离为L。质量mA=1kg的滑块(可视为质点)以v0=12m/s的水平初速度从木板左端滑上木板上表面,滑块与木板上表面的动摩擦因数μ=0.2,假设木板足够长,滑块在此后的运动过程中始终未脱离木板且不会与挡板相碰,木板与挡板相碰过程时间极短且无机械能损失,g=10m/s2,求:
(1)若木板与挡板在第一次碰撞前木板已经做匀速直线运动,则木板右端与挡板的距离至少为多少?
(2)若木板右端与挡板的距离L=2m,木板第一次与挡板碰撞时,滑块的速度的大小?
(3)若木板右端与挡板的距离L=2m,木板至少要多长,滑块才不会脱离木板?(滑块始终未与挡板碰撞)
【答案】、 (1) 8m (2) 8m/s (3) (35.85m或35.9m)
【解析】
(1)木板与滑块共速后将做匀速运动,由动量守恒定律可得:
对B木板,由动能定理可得:
解得 1=8m
(2)对B木板,由动能定理可得:
B与挡板碰撞前,A、B组成的系统动量守恒:
得 vA=8m/s
(3)从A滑上木板到木板与挡板第一次碰撞过程中,A在木板上滑过的距离,由能量守恒定律可得:
解得
B与挡板碰后向左减速,设水平向右为正方向,由己知可得:B与挡板碰后速度,此时A的速度vA=8m/s,由牛顿第二定律可得:
,
木板向左减速,当速度减为零时,由
得 t1=2s
此时B右端距离挡板距离由,得
L2=2m
此时A的速度由,可得:
此时系统总动量向右,设第二次碰撞前A.B已经共速,由动量守恒定律可得:
得
木板从速度为零到v共1经过的位移SB,由,得
故第二次碰前瞬间A、B已经共速,从第一次碰撞到第二次碰撞,A在B上滑过的距离,由能量守恒定律可得:
得
第二次碰撞后B的动量大小大于A的动量大小,故之后B不会再与挡板相碰,对AB由动量守恒可得:
得
从第二次碰撞到最终AB做匀速运动,A在B上滑过距离,由能量守恒定律可得:
得
则 (35.85m或35.9m)
五、爆炸模型
【典例5】(2023北京昌平二模) 如图所示,一枚炮弹发射的初速度为,发射角为。它飞行到最高点时炸裂成质量均为m的A、B两部分,A部分炸裂后竖直下落,B部分继续向前飞行。重力加速度为g,不计空气阻力,不计炸裂过程中炮弹质量的变化。求:
(1)炸裂后瞬间B部分速度的大小和方向;
(2)炸裂前后,A、B系统机械能的变化量
(3)A、B两部分落地点之间的水平距离。
【答案】(1),方向水平向右;(2)机械能增加了;(3)
【解析】
(1)炮弹炸裂前瞬间速度为
方向水平向右
炸裂过程中根据水平方向动量守恒,规定水平向右为正方向,有
炸裂后A部分竖直下落,说明此时A的水平速度为零,解得
方向水平向右
(2)炸裂前后系统机械能的变化量为
解得
A、B系统机械能增加了。
(3)炸裂后,A做自由落体运动,B做平抛运动,下落时间为
落地后,A、B两部分落地点之间的水平距离为
解得
六、弹簧模型
【典例6】. (2023江苏南京市中华中学一模) 如图甲所示,物块A、B的质量分别为2kg、3kg,用轻弹簧拴接,放在光滑的水平地面上,物块B右侧与竖直墙壁接触但不黏连。物块C从t=0时以一定速度向右运动,在t=4s时与物块A相碰,并立即与物块A粘在一起不再分开,物块C的v-t图像如图乙所示,下列说法正确的是( )
A. 物块C的质量为2kg
B. 物块B离开墙壁前,弹簧的最大弹性势能为40.5J
C. 4s到12s的时间内,弹簧对物块A的冲量大小为
D. 物块B离开墙壁后的最大速度为3m/s
【解析】
AC碰撞过程中动量守恒,有
其中、,解得
故A错误;
物块B离开墙壁前,弹簧的最大弹性势能等于AC碰撞结束瞬间系统动能,所以
故B错误;
4s到12s的时间内,弹簧对物块A的冲量大小等于弹簧对AC整体的冲量大小,则
即大小为。故C错误;
物块B离开墙壁后达到最大速度时弹簧处于原长,由动量守恒和机械能守恒可得
,
其中,解得
,
故D正确。
【答案】D
七、人船模型
【典例7】(2023湖北孝感重点高中期中联考)如图,质量为m的人站在质量为M的车的一端,m>M,车相对于地面静止。在人由一端走到另一端的过程中,人重心高度不变,空气阻力、车与地面间的摩擦力均可以忽略不计( )
A. 人对车的冲量大小大于车对人的冲量大小
B. 人发生的位移大小大于车发生的位移大小
C. 人运动越快,人和车的总动量越大
D. 不管人运动多快,车和人的总动量不变
【解析】
在人由一端走到另一端的过程中,对于人和车组成的系统,所受的合外力为零,系统的动量守恒,C错误,D正确。根据,人对车的作用力等于车对人的作用力,作用时间相等,所以人对车的冲量大小等于车对人的冲量大小,A错误;
根据动量守恒定律
两边同时乘于时间,则得
即,m>M
解得,B错误。
【答案】D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
高中物理选择性必修一素养提升学案
第一章 动量守恒定律
综合提升
【知识点图解】
【方法探究】
1.动量定理和动能定理的比较:
动量定理 动能定理
内容 物体所受合外力的冲量等于物体的动量变化量 物体所受合外力的功等于物体动能的变化量
公式 F合t=mv2-mv1 F合s=mv-mv
矢标性 矢量式 标量式
因果关系 因 合外力的冲量 合外力的功(总功)
果 动量的变化 动能的变化
相同点 ①动量定理和动能定理都注重初、末状态而不注重过程,不仅适用于恒力,而且也适用于随时间而变化的力。②不仅适用于单个物体,也适用于物体系统;研究的过程可以是整个过程也可以是某一过程。③动能定理和动量定理既适用于直线运动,也适用于曲线运动。
2.应用动量定理与动能定理的关键词
3. 解决力学问题的三大观点
(1).三种观点的比较
思路 特点分析 适用情况
力的观点:牛顿运动定律结合运动学公式 分析物体的受力,确定加速度,建立加速度和运动量间的关系。涉及力、加速度、位移、速度、时间 恒力作用下的运动
能量观点:动能定理、机械能守恒定律和能量守恒定律 分析物体的受力、位移和速度,确定功与能的关系。系统内力做功会影响系统能量。涉及力、位移、速度 恒力作用下的运动、变力作用下的曲线运动、往复运动、瞬时作用
动量观点:动量定理和动量守恒定律 分析物体的受力(或系统所受外力)、速度,建立力、时间与动量间的关系(或动量守恒定律),系统内力不影响系统动量。涉及力、时间、动量(速度) 恒力作用下的运动、瞬时作用、往复运动
(2).三种观点的选择
(i)对于不涉及物体运动过程中的加速度和时间的问题,无论是恒力做功还是变力做功,一般都利用动能定理求解;如果只有重力和弹簧弹力做功而不涉及运动过程的加速度和时间问题,则采用机械能守恒定律求解。
(ii)对于碰撞、反冲类问题,应用动量守恒定律求解;对于相互作用的两物体,若明确两物体相对滑动的距离,应考虑选用能量守恒(功能关系)建立方程。
4.综合应用动力学“三大观点”解题的步骤:
1 认真审题,明确题目所述的物理情景,确定研究对象.
2 分析所选研究对象的受力情况及运动状态和运动状态的变化过程。对于过程复杂的问题,要正确、合理地把全过程分成若干阶段,注意分析各阶段之间的联系
3 根据各阶段状态变化的规律确定解题方法,选择合理的规律列方程,有时还要分析题目的隐含条件、临界条件、几何关系等列出辅助方程.
4 代入数据 统一单位 ,计算结果,必要时要对结果进行讨论.
【题型探究】
一、动量定理
【典例1】 (2020·甘肃张掖高台一中高二下月考节选)如图所示,质量mA=4.0 kg的木板A放在水平面C上,木板与水平面间的动摩擦因数μ=0.24,木板右端放着质量mB=1.0 kg的小物块B(可视为质点),它们均处于静止状态。木板突然受到水平向右的12 N·s的瞬时冲量作用开始运动,当小物块滑离木板时,木板的动能EkA=8.0 J,小物块的动能EkB=0.5 J,重力加速度g取10 m/s2,求:
(1)瞬时冲量作用结束时木板的速度大小v0;
(2)木板的长度L。
[解析] (1)在瞬时冲量作用时,木板A受水平面和小物块B的摩擦力的冲量均可以忽略。
取水平向右为正方向,对木板A,由动量定理有I=mAv0,代入数据解得v0=3 m/s。
(2)设A对B、B对A、C对A的滑动摩擦力大小分别为FfAB、FfBA、FfCA,B在A上滑行的时间为t,B离开A时A的速度为vA,B的速度为vB,A、B相对C的位移为sA、sB。
对A,由动量定理有-(FfBA+FfCA)t=mAvA-mAv0,
对B,由动量定理有FfABt=mBvB,
由牛顿第三定律可得FfBA=FfAB,另FfCA=μ(mA+mB)g,
对A,由动能定理有-(FfBA+FfCA)sA=mAv-mAv,
对B,由动能定理有FfABsB=mBv,
根据动量与动能之间的关系有mAvA=,
mBvB=,
木板A的长度即B相对A滑动距离的大小,故L=sA-sB,
联立解得L=0.5 m。
[答案] (1)3 m/s (2)0.5 m
[一语通关] 1 动量定理和动能定理都是求解力学问题的重要定理。应用时要特别注意选定研究对象和过程,注重受力情况分析和运动情况分析,灵活运用规律求解。
2 运用动量定理解题需考虑速度的方向,运用动能定理解题则不需考虑速度的方向。
二、碰撞
【典例2】 如图所示,质量分别为mA、mB的两个弹性小球A、B静止在地面上方,B球距地面的高度h=0.8 m,A球在B球的正上方。先将B球释放,经过一段时间后再将A球释放。当A球下落t=0.3 s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰好为零。已知mB=3mA,重力加速度大小g取10 m/s2,忽略空气阻力及碰撞中的动能损失。求:
(1)B球第一次到达地面时的速度;
(2)P点距离地面的高度。
[解析] (1)设B球第一次到达地面时的速度大小为vB,由运动学公式有vB=,
将h=0.8 m代入上式,得vB=4 m/s。
(2)设两球相碰前后,A球的速度大小分别为v1和v1′(v1′=0),B球的速度分别为v2和v2′,
由运动学规律可得v1=gt,
由于碰撞时间极短,重力的作用可以忽略,两球相碰前后的动量守恒,总动能保持不变。规定竖直向下的方向为正方向,有mAv1+mBv2=mBv2′,
mAv+mBv=mBv2′2,
设B球与地面相碰后的速度大小为vB′,忽略碰撞中的动能损失可得vB′=vB,
设P点距地面的高度为h′,由运动学规律可得
h′=,
联立各式,并代入已知条件可得
h′=0.75 m。
[答案] (1)4 m/s (2)0.75 m
三、反冲
【典例3】反冲小车静止放在水平光滑玻璃上,点燃酒精,蒸汽将橡皮塞水平喷出,小车沿相反方向运动。如果小车运动前的总质量M=3 kg,水平喷出的橡皮塞的质量m=0.1 kg。
(1)若橡皮塞喷出时获得的水平速度v=2.9 m/s,求小车的反冲速度;
(2)若橡皮塞喷出时速度大小不变,方向与水平方向成60°角,小车的反冲速度又如何(小车一直在水平方向运动)
[解析] (1)以橡皮塞运动的方向为正方向,根据动量守恒定律有
mv+(M-m)v′=0
v′=-v=-×2.9 m/s=-0.1 m/s
负号表示小车的运动方向与橡皮塞运动的方向相反。
(2)以橡皮塞运动的水平分运动方向为正方向,有
mvcos 60°+(M-m)v″=0
v″=-=- m/s=-0.05 m/s
负号表示小车的运动方向与橡皮塞运动的水平分运动的方向相反。
[答案] (1)0.1 m/s,方向与橡皮塞运动的方向相反
(2)0.05 m/s,方向与橡皮塞运动的水平分运动的方向相反
四、滑块木板模型
【典例4】.(16分)(2023北京昌平模拟)如图所示,光滑水平地面上固定一竖直挡板P,质量mB=2kg的木板B静止在水平面上,木板右端与挡板P的距离为L。质量mA=1kg的滑块(可视为质点)以v0=12m/s的水平初速度从木板左端滑上木板上表面,滑块与木板上表面的动摩擦因数μ=0.2,假设木板足够长,滑块在此后的运动过程中始终未脱离木板且不会与挡板相碰,木板与挡板相碰过程时间极短且无机械能损失,g=10m/s2,求:
(1)若木板与挡板在第一次碰撞前木板已经做匀速直线运动,则木板右端与挡板的距离至少为多少?
(2)若木板右端与挡板的距离L=2m,木板第一次与挡板碰撞时,滑块的速度的大小?
(3)若木板右端与挡板的距离L=2m,木板至少要多长,滑块才不会脱离木板?(滑块始终未与挡板碰撞)
【答案】、 (1) 8m (2) 8m/s (3) (35.85m或35.9m)
【解析】
(1)木板与滑块共速后将做匀速运动,由动量守恒定律可得:
对B木板,由动能定理可得:
解得 1=8m
(2)对B木板,由动能定理可得:
B与挡板碰撞前,A、B组成的系统动量守恒:
得 vA=8m/s
(3)从A滑上木板到木板与挡板第一次碰撞过程中,A在木板上滑过的距离,由能量守恒定律可得:
解得
B与挡板碰后向左减速,设水平向右为正方向,由己知可得:B与挡板碰后速度,此时A的速度vA=8m/s,由牛顿第二定律可得:
,
木板向左减速,当速度减为零时,由
得 t1=2s
此时B右端距离挡板距离由,得
L2=2m
此时A的速度由,可得:
此时系统总动量向右,设第二次碰撞前A.B已经共速,由动量守恒定律可得:
得
木板从速度为零到v共1经过的位移SB,由,得
故第二次碰前瞬间A、B已经共速,从第一次碰撞到第二次碰撞,A在B上滑过的距离,由能量守恒定律可得:
得
第二次碰撞后B的动量大小大于A的动量大小,故之后B不会再与挡板相碰,对AB由动量守恒可得:
得
从第二次碰撞到最终AB做匀速运动,A在B上滑过距离,由能量守恒定律可得:
得
则 (35.85m或35.9m)
五、爆炸模型
【典例5】(2023北京昌平二模) 如图所示,一枚炮弹发射的初速度为,发射角为。它飞行到最高点时炸裂成质量均为m的A、B两部分,A部分炸裂后竖直下落,B部分继续向前飞行。重力加速度为g,不计空气阻力,不计炸裂过程中炮弹质量的变化。求:
(1)炸裂后瞬间B部分速度的大小和方向;
(2)炸裂前后,A、B系统机械能的变化量
(3)A、B两部分落地点之间的水平距离。
【答案】(1),方向水平向右;(2)机械能增加了;(3)
【解析】
(1)炮弹炸裂前瞬间速度为
方向水平向右
炸裂过程中根据水平方向动量守恒,规定水平向右为正方向,有
炸裂后A部分竖直下落,说明此时A的水平速度为零,解得
方向水平向右
(2)炸裂前后系统机械能的变化量为
解得
A、B系统机械能增加了。
(3)炸裂后,A做自由落体运动,B做平抛运动,下落时间为
落地后,A、B两部分落地点之间的水平距离为
解得
六、弹簧模型
【典例6】. (2023江苏南京市中华中学一模) 如图甲所示,物块A、B的质量分别为2kg、3kg,用轻弹簧拴接,放在光滑的水平地面上,物块B右侧与竖直墙壁接触但不黏连。物块C从t=0时以一定速度向右运动,在t=4s时与物块A相碰,并立即与物块A粘在一起不再分开,物块C的v-t图像如图乙所示,下列说法正确的是( )
A. 物块C的质量为2kg
B. 物块B离开墙壁前,弹簧的最大弹性势能为40.5J
C. 4s到12s的时间内,弹簧对物块A的冲量大小为
D. 物块B离开墙壁后的最大速度为3m/s
【解析】
AC碰撞过程中动量守恒,有
其中、,解得
故A错误;
物块B离开墙壁前,弹簧的最大弹性势能等于AC碰撞结束瞬间系统动能,所以
故B错误;
4s到12s的时间内,弹簧对物块A的冲量大小等于弹簧对AC整体的冲量大小,则
即大小为。故C错误;
物块B离开墙壁后达到最大速度时弹簧处于原长,由动量守恒和机械能守恒可得
,
其中,解得
,
故D正确。
【答案】D
七、人船模型
【典例7】(2023湖北孝感重点高中期中联考)如图,质量为m的人站在质量为M的车的一端,m>M,车相对于地面静止。在人由一端走到另一端的过程中,人重心高度不变,空气阻力、车与地面间的摩擦力均可以忽略不计( )
A. 人对车的冲量大小大于车对人的冲量大小
B. 人发生的位移大小大于车发生的位移大小
C. 人运动越快,人和车的总动量越大
D. 不管人运动多快,车和人的总动量不变
【解析】
在人由一端走到另一端的过程中,对于人和车组成的系统,所受的合外力为零,系统的动量守恒,C错误,D正确。根据,人对车的作用力等于车对人的作用力,作用时间相等,所以人对车的冲量大小等于车对人的冲量大小,A错误;
根据动量守恒定律
两边同时乘于时间,则得
即,m>M
解得,B错误。
【答案】D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
