第16章 二次根式 培优测试题(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
第1章 整式的乘除 综合素质测试
考试范围:第1章 整式的乘除;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.计算:m2 m,结果正确的是( )
A.2m2 B.m3 C.2m3 D.m2
2.下列计算正确的是( )
A.a2+a3=a5 B.a3+b3=(a+b)(a2﹣ab+b2)
C.(a+b)2=a2﹣2ab+b2 D.a6÷a3=a2
3.花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为( )
A.3.7×10﹣5克 B.3.7×10﹣6克
C.37×10﹣7克 D.3.7×10﹣8克
4.计算(﹣2xy2)3,其中第①步运算的依据是( )
A.幂的乘方法则 B.乘法分配律
C.积的乘方法则 D.同底数幂的乘法法则
5.若x2﹣2x﹣m=(x+n)(x﹣3),则m+n的值为( )
A.4 B.8 C.﹣4 D.6
6.若a,b是正整数,且满足,则a与b的关系正确的是( )
A.a+3=8b B.3a=8b C.a+3=b8 D.3a=8+b
7.我们知道可以用一些硬纸片拼成的图形面积来解释些代数恒等式,例如图1可以用来解释(a+b)2﹣(a﹣b)2=4ab,那么通过图2面积的计算,验证了一个恒等式,此等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)(a+2b)=a2+ab﹣2b
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
8.若m=275,n=345,则m、n的大小关系正确的是( )
A.m>n B.m<n
C.相等 D.大小关系无法确定
9.我们知道:若am=an(a>0且a≠1),则m=n.设5m=3,5n=15,5p=75.现给出m,n,p三者之间的三个关系式:①m+p=2n;②m+n=2p﹣1;③n2﹣mp=1.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
10.如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为5cm,下列说法中正确的是( )
①小长方形的较长边为y﹣15;②阴影A的较短边和阴影B的较短边之和为x﹣y+5;
③若x为定值,则阴影A和阴影B的周长和为定值;④当x=15时,阴影A和阴影B的面积和为定值.
A.①③④ B.②④ C.①③ D.①④
二.填空题(共5小题,满分15分,每小题3分)
11.计算(x3y)2的结果等于 .
12.计算:﹣3﹣2+()0﹣(﹣1)﹣4= .
13.“先看到闪电,后听到雷声”,那是因为在空气中光的传播速度比声音快.科学家发现,光在空气里的传播速度约为3×108米/秒,而声音在空气里的传播速度大约为3×102米/秒.在空气中光的速度是声速的 倍.
14.设a,b是实数,定义关于“*”的一种运算:a*b=(a+b)2﹣(a﹣b)2,则下列结论:①若a*b=0,则a=0或b=0;②不存在实数a,b,满足a*b=a2+4b2;③a*(b+c)=a*b+a*c;④若a*b=8,则(10ab3)÷(5b2)=4.其中正确的是 .(填写序号)
15.若(x﹣3)(x2+ax+b)的积中不含x的二次项和一次项,则a+b的值为 .
三.解答题(共8小题,满分75分)
16.(9分)计算.
(1)82022×(﹣0.125)2023; (2)12342﹣1234×268+1342;
(3).
17.(8分)计算:
(1)3a2 2a4+(3a3)2﹣14a6; (2)2x(x﹣3y)﹣(5xy2﹣2x2y)÷y.
18.(9分)已知关于x的二次三项式A满足A﹣(x﹣1)(x+1)=(x+1)2.
(1)求整式A;
(2)若B=3x2+4x+2,当x时,求B﹣A的值.
19.(9分)位于太原市三给片区的天美杉杉超级奥特莱斯是一座集现代化商业、中式文化与绿色园林三位一体的大型综合商业体,值得期待的是将于2023年9月开始正式营业.如图,在园区内有一块长为(a+4b)米,宽为(a+b)米的长方形地块,现规划将阴影部分进行绿化,中间预留部分是边长为(a﹣b)米的正方形.
(1)求绿化的面积S(用含a,b的代数式表示,并化简);
(2)若a=3,b=2,绿化成本为100元/平方米,则完成绿化共需要多少元?
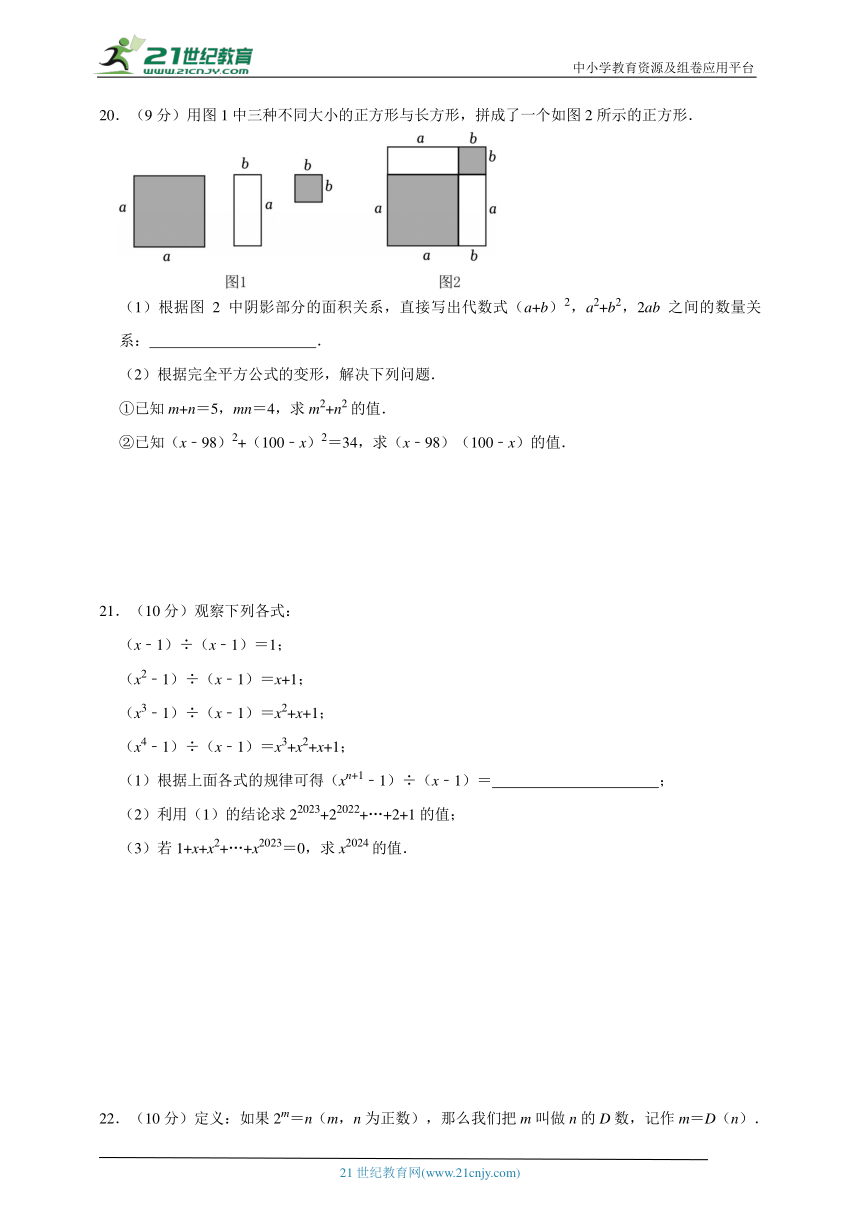
20.(9分)用图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)根据图2中阴影部分的面积关系,直接写出代数式(a+b)2,a2+b2,2ab之间的数量关系: .
(2)根据完全平方公式的变形,解决下列问题.
①已知m+n=5,mn=4,求m2+n2的值.
②已知(x﹣98)2+(100﹣x)2=34,求(x﹣98)(100﹣x)的值.
21.(10分)观察下列各式:
(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1;
(1)根据上面各式的规律可得(xn+1﹣1)÷(x﹣1)= ;
(2)利用(1)的结论求22023+22022+…+2+1的值;
(3)若1+x+x2+…+x2023=0,求x2024的值.
22.(10分)定义:如果2m=n(m,n为正数),那么我们把m叫做n的D数,记作m=D(n).
(1)根据D数的定义,填空:D(2)= ,D(16)= .
(2)D数有如下运算性质:D(s t)=D(s)+D(t),D()=D(q)﹣D(p),其中q>p.
根据运算性质,计算:
①若D(a)=1,求D(a3);
②若已知D(3)=2a﹣b,D(5)=a+c,试求D(15),D(),D(108),D()的值(用a、b、c表示).
23.(11分)在学习多项式乘以多项式时,我们知道(x+4)(2x+5)(3x﹣6)的结果是一个多项式,并且最高次项为x 2x 3x=3x3,常数项为4×5×(﹣6)=﹣120.那么一次项是多少呢?
要解决这个问题,就是要确定该一次项的系数.通过观察,我们发现一次项系数就是:5×(﹣6)+4×2×(﹣6)+4×5×3=﹣3,即一次项为﹣3x.
参考材料中用到的方法,解决下列问题:
(1)计算(x+2)(3x+1)(5x﹣3)所得多项式的一次项系数;
(2)如果计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所得多项式不含一次项,求a的值.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:m2 m=m3.
选:B.
2.解:A、a2与a3不是同类项,不能合并,不符合题意;
B、a3+b3=(a+b)(a2﹣ab+b2),计算正确,符合题意;
C、(a+b)2=a2+2ab+b2,计算不正确,不符合题意;
D、a6÷a3=a3,计算不正确,不符合题意.
选:B.
3.解:0.000037毫克=0.000000037克
0.000000037=3.7×10﹣8,
选:D.
4.解:(﹣2xy2)3=(﹣2)3x3(y2)3,
其运算依据是积的乘方法则,
选:C.
5.解:已知等式整理得:x2﹣2x﹣m=(x+n)(x﹣3)=x2+(n﹣3)x﹣3n,
可得n﹣3=﹣2,﹣3n=﹣m,
解得:m=3,n=1,
则m+n=3+1=4.
选:A.
6.解:根据已知得,8×2a=28b,
即2a+3=28b,
∴a+3=8b.
选:A.
7.解:
空白部分的面积:(a﹣b)2,
还可以表示为:a2﹣2ab+b2,
∴此等式是(a﹣b)2=a2﹣2ab+b2.
选:D.
8.解:∵m=275=(25)15=3215,
n=345=(33)15=2715,
又∵32>27,
∴3215>2715,
即m>n.
选:A.
9.解:∵5m=3,
∴5n=15=5×3=5×5m=51+m,
∴n=1+m,
∵5p=75=52×3=52+m,
∴p=2+m,
∴p=n+1,
①m+p=n﹣1+n+1=2n,此结论正确;
②m+n=p﹣2+p﹣1=2p﹣3,此结论错误;
③n2﹣mp=(1+m)2﹣m(2+m)
=1+m2+2m﹣2m﹣m2
=1,此结论正确;
正确的是:①③.
选:B.
10.解:①∵大长方形的长为y cm,小长方形的宽为5cm,
∴小长方形的长为y﹣3×5=(y﹣15)cm,说法①正确;
②∵大长方形的宽为x cm,小长方形的长为(y﹣15)cm,小长方形的宽为5cm,
∴阴影A的较短边为x﹣2×5=(x﹣10)cm,阴影B的较短边为x﹣(y﹣15)=(x﹣y+15)cm,
∴阴影A的较短边和阴影B的较短边之和为x﹣10+x﹣y+15=(2x+5﹣y)cm,说法②错误;
③∵阴影A的较长边为(y﹣15)cm,较短边为(x﹣10)cm,阴影B的较长边为3×5=15cm,较短边为(x﹣y+15)cm,
∴阴影A的周长为2(y﹣15+x﹣10)=2(x+y﹣25),阴影B的周长为2(15+x﹣y+15)=2(x﹣y+30),
∴阴影A和阴影B的周长之和为2(x+y﹣25)+2(x﹣y+30)=2(2x+5),
∴若x为定值,则阴影A和阴影B的周长之和为定值,说法③正确;
④∵阴影A的较长边为(y﹣15)cm,较短边为(x﹣10)cm,阴影B的较长边为3×5=15cm,较短边为(x﹣y+15)cm,
∴阴影A的面积为(y﹣15)(x﹣10)=(xy﹣15x﹣10y+150)cm2,阴影B的面积为15(x﹣y+15)=(15x﹣15y+225)cm2,
∴阴影A和阴影B的面积之和为xy﹣15x﹣10y+150+15x﹣15y+225=(xy﹣25y+375)cm2,
当x=15时,xy﹣25y+375=(375﹣10y)cm2,说法④错误.
综上所述,正确的说法有①③.
选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.解:原式=(x3)2 y2
=x6y2,
答案为:x6y2.
12.解:原式1﹣1.
答案为:,
13.解:3×108米/秒÷3×102米/秒=106,
答案为:106
14.解:根据题中的新定义得:
①若a*b=(a+b)2﹣(a﹣b)2=4ab=0,则a=0或b=0,符合题意;
②若满足a*b=(a+b)2﹣(a﹣b)2=4ab=a2+4b2,即a2﹣4ab+4b2=(a﹣2b)2=0,
则当a=2b时,a*b=a2+4b2,不符合题意;
③a*(b+c)=(a+b+c)2﹣(a﹣b﹣c)2=4a(b+c)=4ab+4ac,
a*b+a*c=(a+b)2﹣(a﹣b)2+(a+c)2﹣(a﹣c)2=4ab+4ac,
则a*(b+c)=a*b+a*c,符合题意;
④若a*b=(a+b)2﹣(a﹣b)2=4ab=8,即ab=2,
则(10ab3)÷(5b2)=2ab=4,符合题意.
其中正确的是①③④.
答案为:①③④.
15.解:原式=x3+ax2+bx﹣3x2﹣3ax﹣3b
=x3+(a﹣3)x2+(b﹣3a)x﹣3b,
由积中不含x的二次项和一次项,
得到a﹣3=0,b﹣3a=0,
解得:a=3,b=9,
则a+b=3+9=12.
答案为:12.
三.解答题(共8小题,满分75分)
16.解:(1)82022×(﹣0.125)2023
=82022×(﹣0.125)2022×(﹣0.125)
=(﹣0.125×8)2022×(﹣0.125)
=(﹣1)2022×(﹣0.125)
=1×(﹣0.125)
=﹣0.125;
(2)12342﹣1234×268+1342
=12342﹣2×1234×134+1342
=(1234﹣134)2
=11002
=1210000;
(3)
=(100)×(﹣100)
=()2﹣1002
10000
.
17.解:(1)原式=6a6+9a6﹣14a6
=a6;
(2)原式=2x2﹣6xy﹣5xy+2x2
=4x2﹣11xy.
18.解:(1)∵A﹣(x﹣1)(x+1)=(x+1)2,
∴A=(x+1)2+(x﹣1)(x+1)
=x2+2x+1+x2﹣1
=2x2+2x;
(2)∵B=3x2+4x+2,A=2x2+2x,
∴B﹣A=3x2+4x+2﹣(2x2+2x)
=3x2+4x+2﹣2x2﹣2x
=x2+2x+2
当x时,
B﹣A=()2+2×()+2
1+2
.
19.解:(1)由题意得,
阴影部分的面积为(a+4b)(a+b)﹣(a﹣b)2
=a2+5ab+4b2,﹣a2+2ab﹣b2
=(7ab+3b2)平方米,
(2)当a=3,b=2时,7ab+3b2=7×3×2+3×22=54(平方米),
所需费用为100×54=5400(元),
答:完成绿化共需要5400元.
20.解:(1)根据图形面积可知,a2+b2=(a+b)2﹣2ab,
答案为:a2+b2=(a+b)2﹣2ab;
(2)①根据题意可知,
m2+n2=(m+n)2﹣2mn
=25﹣2×4
=17;
②∵x﹣98+100﹣x=2,(x﹣98)2+(100﹣x)2=34,
∴原式=(x﹣98)2+(100﹣x)2+2(x﹣98)(100﹣x)
=34+2(x﹣98)(100﹣x),
即4=34+2(x﹣98)(100﹣x),
解得:(x﹣98)(100﹣x)=﹣15.
21.解:(1)根据题意得:结果的规律:按x进行降幂排列,各项系数为1,最高次项的次数为等式前面的最高次数减1,
∴(xn+1﹣1)÷(x﹣1)=xn+xn﹣1+ +x+1,
答案为:xn+xn﹣1+ +x+1;
(2)22023+22022+ +2+1=(22024﹣1)÷(2﹣1)=22024﹣1
(3)由1+x+x2+ +x2023=0可得,
(x2024﹣1)÷(x﹣1)=0,
∴x2024﹣1=0,且x﹣1≠0,
∴x2024=1.
22.解:(1)∵21=2,
∴D(2)=1,
∵24=16,
∴D(16)=4,
答案为:1;4.
(2)①∵21=a,
∴a=2.
∴23=23.
∴D(a3)=3.
②D(15)=D(3×5),
=D(3)+D(5)
=(2a﹣b)+(a+c)
=3a﹣b+c,
=(a+c)﹣(2a﹣b)
=﹣a+b+c.
D(108)=D(3×3×3×2×2),
=D(3)+D(3)+D(3)+D(2)+D(2)
=3×D(3)+2×D(2)
=3×(2a﹣b)+2×1
=6a﹣3b+2.
,
=D(3×3×3)﹣D(5×2×2)
=D(3)+D(3)+D(3)﹣[D(5)+D(2)+D(2)]
=3×D(3)﹣[D(5)+2D(2)]
=3×(2a﹣b)﹣[a+c+2×1]
=6a﹣3b﹣a﹣c﹣2
=5a﹣3b﹣c﹣2,
23.解:(1)(x+2)(3x+1)(5x﹣3)所得多项式的一次项系数为:
1×1×(﹣3)+2×3×(﹣3)+2×1×5
=﹣3﹣18+10
=﹣11;
(2)(x2+x+1)(x2﹣3x+a)(2x﹣1)所得多项式一次项系数为:
1×a×(﹣1)+1×(﹣3)×(﹣1)+1×a×2
=﹣a+3+2a
=a+3,
∵多项式不含一次项,
∴a+3=0,
解得:a=﹣3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第1章 整式的乘除 综合素质测试
考试范围:第1章 整式的乘除;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.计算:m2 m,结果正确的是( )
A.2m2 B.m3 C.2m3 D.m2
2.下列计算正确的是( )
A.a2+a3=a5 B.a3+b3=(a+b)(a2﹣ab+b2)
C.(a+b)2=a2﹣2ab+b2 D.a6÷a3=a2
3.花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为( )
A.3.7×10﹣5克 B.3.7×10﹣6克
C.37×10﹣7克 D.3.7×10﹣8克
4.计算(﹣2xy2)3,其中第①步运算的依据是( )
A.幂的乘方法则 B.乘法分配律
C.积的乘方法则 D.同底数幂的乘法法则
5.若x2﹣2x﹣m=(x+n)(x﹣3),则m+n的值为( )
A.4 B.8 C.﹣4 D.6
6.若a,b是正整数,且满足,则a与b的关系正确的是( )
A.a+3=8b B.3a=8b C.a+3=b8 D.3a=8+b
7.我们知道可以用一些硬纸片拼成的图形面积来解释些代数恒等式,例如图1可以用来解释(a+b)2﹣(a﹣b)2=4ab,那么通过图2面积的计算,验证了一个恒等式,此等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)(a+2b)=a2+ab﹣2b
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
8.若m=275,n=345,则m、n的大小关系正确的是( )
A.m>n B.m<n
C.相等 D.大小关系无法确定
9.我们知道:若am=an(a>0且a≠1),则m=n.设5m=3,5n=15,5p=75.现给出m,n,p三者之间的三个关系式:①m+p=2n;②m+n=2p﹣1;③n2﹣mp=1.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
10.如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为5cm,下列说法中正确的是( )
①小长方形的较长边为y﹣15;②阴影A的较短边和阴影B的较短边之和为x﹣y+5;
③若x为定值,则阴影A和阴影B的周长和为定值;④当x=15时,阴影A和阴影B的面积和为定值.
A.①③④ B.②④ C.①③ D.①④
二.填空题(共5小题,满分15分,每小题3分)
11.计算(x3y)2的结果等于 .
12.计算:﹣3﹣2+()0﹣(﹣1)﹣4= .
13.“先看到闪电,后听到雷声”,那是因为在空气中光的传播速度比声音快.科学家发现,光在空气里的传播速度约为3×108米/秒,而声音在空气里的传播速度大约为3×102米/秒.在空气中光的速度是声速的 倍.
14.设a,b是实数,定义关于“*”的一种运算:a*b=(a+b)2﹣(a﹣b)2,则下列结论:①若a*b=0,则a=0或b=0;②不存在实数a,b,满足a*b=a2+4b2;③a*(b+c)=a*b+a*c;④若a*b=8,则(10ab3)÷(5b2)=4.其中正确的是 .(填写序号)
15.若(x﹣3)(x2+ax+b)的积中不含x的二次项和一次项,则a+b的值为 .
三.解答题(共8小题,满分75分)
16.(9分)计算.
(1)82022×(﹣0.125)2023; (2)12342﹣1234×268+1342;
(3).
17.(8分)计算:
(1)3a2 2a4+(3a3)2﹣14a6; (2)2x(x﹣3y)﹣(5xy2﹣2x2y)÷y.
18.(9分)已知关于x的二次三项式A满足A﹣(x﹣1)(x+1)=(x+1)2.
(1)求整式A;
(2)若B=3x2+4x+2,当x时,求B﹣A的值.
19.(9分)位于太原市三给片区的天美杉杉超级奥特莱斯是一座集现代化商业、中式文化与绿色园林三位一体的大型综合商业体,值得期待的是将于2023年9月开始正式营业.如图,在园区内有一块长为(a+4b)米,宽为(a+b)米的长方形地块,现规划将阴影部分进行绿化,中间预留部分是边长为(a﹣b)米的正方形.
(1)求绿化的面积S(用含a,b的代数式表示,并化简);
(2)若a=3,b=2,绿化成本为100元/平方米,则完成绿化共需要多少元?
20.(9分)用图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)根据图2中阴影部分的面积关系,直接写出代数式(a+b)2,a2+b2,2ab之间的数量关系: .
(2)根据完全平方公式的变形,解决下列问题.
①已知m+n=5,mn=4,求m2+n2的值.
②已知(x﹣98)2+(100﹣x)2=34,求(x﹣98)(100﹣x)的值.
21.(10分)观察下列各式:
(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1;
(1)根据上面各式的规律可得(xn+1﹣1)÷(x﹣1)= ;
(2)利用(1)的结论求22023+22022+…+2+1的值;
(3)若1+x+x2+…+x2023=0,求x2024的值.
22.(10分)定义:如果2m=n(m,n为正数),那么我们把m叫做n的D数,记作m=D(n).
(1)根据D数的定义,填空:D(2)= ,D(16)= .
(2)D数有如下运算性质:D(s t)=D(s)+D(t),D()=D(q)﹣D(p),其中q>p.
根据运算性质,计算:
①若D(a)=1,求D(a3);
②若已知D(3)=2a﹣b,D(5)=a+c,试求D(15),D(),D(108),D()的值(用a、b、c表示).
23.(11分)在学习多项式乘以多项式时,我们知道(x+4)(2x+5)(3x﹣6)的结果是一个多项式,并且最高次项为x 2x 3x=3x3,常数项为4×5×(﹣6)=﹣120.那么一次项是多少呢?
要解决这个问题,就是要确定该一次项的系数.通过观察,我们发现一次项系数就是:5×(﹣6)+4×2×(﹣6)+4×5×3=﹣3,即一次项为﹣3x.
参考材料中用到的方法,解决下列问题:
(1)计算(x+2)(3x+1)(5x﹣3)所得多项式的一次项系数;
(2)如果计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所得多项式不含一次项,求a的值.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:m2 m=m3.
选:B.
2.解:A、a2与a3不是同类项,不能合并,不符合题意;
B、a3+b3=(a+b)(a2﹣ab+b2),计算正确,符合题意;
C、(a+b)2=a2+2ab+b2,计算不正确,不符合题意;
D、a6÷a3=a3,计算不正确,不符合题意.
选:B.
3.解:0.000037毫克=0.000000037克
0.000000037=3.7×10﹣8,
选:D.
4.解:(﹣2xy2)3=(﹣2)3x3(y2)3,
其运算依据是积的乘方法则,
选:C.
5.解:已知等式整理得:x2﹣2x﹣m=(x+n)(x﹣3)=x2+(n﹣3)x﹣3n,
可得n﹣3=﹣2,﹣3n=﹣m,
解得:m=3,n=1,
则m+n=3+1=4.
选:A.
6.解:根据已知得,8×2a=28b,
即2a+3=28b,
∴a+3=8b.
选:A.
7.解:
空白部分的面积:(a﹣b)2,
还可以表示为:a2﹣2ab+b2,
∴此等式是(a﹣b)2=a2﹣2ab+b2.
选:D.
8.解:∵m=275=(25)15=3215,
n=345=(33)15=2715,
又∵32>27,
∴3215>2715,
即m>n.
选:A.
9.解:∵5m=3,
∴5n=15=5×3=5×5m=51+m,
∴n=1+m,
∵5p=75=52×3=52+m,
∴p=2+m,
∴p=n+1,
①m+p=n﹣1+n+1=2n,此结论正确;
②m+n=p﹣2+p﹣1=2p﹣3,此结论错误;
③n2﹣mp=(1+m)2﹣m(2+m)
=1+m2+2m﹣2m﹣m2
=1,此结论正确;
正确的是:①③.
选:B.
10.解:①∵大长方形的长为y cm,小长方形的宽为5cm,
∴小长方形的长为y﹣3×5=(y﹣15)cm,说法①正确;
②∵大长方形的宽为x cm,小长方形的长为(y﹣15)cm,小长方形的宽为5cm,
∴阴影A的较短边为x﹣2×5=(x﹣10)cm,阴影B的较短边为x﹣(y﹣15)=(x﹣y+15)cm,
∴阴影A的较短边和阴影B的较短边之和为x﹣10+x﹣y+15=(2x+5﹣y)cm,说法②错误;
③∵阴影A的较长边为(y﹣15)cm,较短边为(x﹣10)cm,阴影B的较长边为3×5=15cm,较短边为(x﹣y+15)cm,
∴阴影A的周长为2(y﹣15+x﹣10)=2(x+y﹣25),阴影B的周长为2(15+x﹣y+15)=2(x﹣y+30),
∴阴影A和阴影B的周长之和为2(x+y﹣25)+2(x﹣y+30)=2(2x+5),
∴若x为定值,则阴影A和阴影B的周长之和为定值,说法③正确;
④∵阴影A的较长边为(y﹣15)cm,较短边为(x﹣10)cm,阴影B的较长边为3×5=15cm,较短边为(x﹣y+15)cm,
∴阴影A的面积为(y﹣15)(x﹣10)=(xy﹣15x﹣10y+150)cm2,阴影B的面积为15(x﹣y+15)=(15x﹣15y+225)cm2,
∴阴影A和阴影B的面积之和为xy﹣15x﹣10y+150+15x﹣15y+225=(xy﹣25y+375)cm2,
当x=15时,xy﹣25y+375=(375﹣10y)cm2,说法④错误.
综上所述,正确的说法有①③.
选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.解:原式=(x3)2 y2
=x6y2,
答案为:x6y2.
12.解:原式1﹣1.
答案为:,
13.解:3×108米/秒÷3×102米/秒=106,
答案为:106
14.解:根据题中的新定义得:
①若a*b=(a+b)2﹣(a﹣b)2=4ab=0,则a=0或b=0,符合题意;
②若满足a*b=(a+b)2﹣(a﹣b)2=4ab=a2+4b2,即a2﹣4ab+4b2=(a﹣2b)2=0,
则当a=2b时,a*b=a2+4b2,不符合题意;
③a*(b+c)=(a+b+c)2﹣(a﹣b﹣c)2=4a(b+c)=4ab+4ac,
a*b+a*c=(a+b)2﹣(a﹣b)2+(a+c)2﹣(a﹣c)2=4ab+4ac,
则a*(b+c)=a*b+a*c,符合题意;
④若a*b=(a+b)2﹣(a﹣b)2=4ab=8,即ab=2,
则(10ab3)÷(5b2)=2ab=4,符合题意.
其中正确的是①③④.
答案为:①③④.
15.解:原式=x3+ax2+bx﹣3x2﹣3ax﹣3b
=x3+(a﹣3)x2+(b﹣3a)x﹣3b,
由积中不含x的二次项和一次项,
得到a﹣3=0,b﹣3a=0,
解得:a=3,b=9,
则a+b=3+9=12.
答案为:12.
三.解答题(共8小题,满分75分)
16.解:(1)82022×(﹣0.125)2023
=82022×(﹣0.125)2022×(﹣0.125)
=(﹣0.125×8)2022×(﹣0.125)
=(﹣1)2022×(﹣0.125)
=1×(﹣0.125)
=﹣0.125;
(2)12342﹣1234×268+1342
=12342﹣2×1234×134+1342
=(1234﹣134)2
=11002
=1210000;
(3)
=(100)×(﹣100)
=()2﹣1002
10000
.
17.解:(1)原式=6a6+9a6﹣14a6
=a6;
(2)原式=2x2﹣6xy﹣5xy+2x2
=4x2﹣11xy.
18.解:(1)∵A﹣(x﹣1)(x+1)=(x+1)2,
∴A=(x+1)2+(x﹣1)(x+1)
=x2+2x+1+x2﹣1
=2x2+2x;
(2)∵B=3x2+4x+2,A=2x2+2x,
∴B﹣A=3x2+4x+2﹣(2x2+2x)
=3x2+4x+2﹣2x2﹣2x
=x2+2x+2
当x时,
B﹣A=()2+2×()+2
1+2
.
19.解:(1)由题意得,
阴影部分的面积为(a+4b)(a+b)﹣(a﹣b)2
=a2+5ab+4b2,﹣a2+2ab﹣b2
=(7ab+3b2)平方米,
(2)当a=3,b=2时,7ab+3b2=7×3×2+3×22=54(平方米),
所需费用为100×54=5400(元),
答:完成绿化共需要5400元.
20.解:(1)根据图形面积可知,a2+b2=(a+b)2﹣2ab,
答案为:a2+b2=(a+b)2﹣2ab;
(2)①根据题意可知,
m2+n2=(m+n)2﹣2mn
=25﹣2×4
=17;
②∵x﹣98+100﹣x=2,(x﹣98)2+(100﹣x)2=34,
∴原式=(x﹣98)2+(100﹣x)2+2(x﹣98)(100﹣x)
=34+2(x﹣98)(100﹣x),
即4=34+2(x﹣98)(100﹣x),
解得:(x﹣98)(100﹣x)=﹣15.
21.解:(1)根据题意得:结果的规律:按x进行降幂排列,各项系数为1,最高次项的次数为等式前面的最高次数减1,
∴(xn+1﹣1)÷(x﹣1)=xn+xn﹣1+ +x+1,
答案为:xn+xn﹣1+ +x+1;
(2)22023+22022+ +2+1=(22024﹣1)÷(2﹣1)=22024﹣1
(3)由1+x+x2+ +x2023=0可得,
(x2024﹣1)÷(x﹣1)=0,
∴x2024﹣1=0,且x﹣1≠0,
∴x2024=1.
22.解:(1)∵21=2,
∴D(2)=1,
∵24=16,
∴D(16)=4,
答案为:1;4.
(2)①∵21=a,
∴a=2.
∴23=23.
∴D(a3)=3.
②D(15)=D(3×5),
=D(3)+D(5)
=(2a﹣b)+(a+c)
=3a﹣b+c,
=(a+c)﹣(2a﹣b)
=﹣a+b+c.
D(108)=D(3×3×3×2×2),
=D(3)+D(3)+D(3)+D(2)+D(2)
=3×D(3)+2×D(2)
=3×(2a﹣b)+2×1
=6a﹣3b+2.
,
=D(3×3×3)﹣D(5×2×2)
=D(3)+D(3)+D(3)﹣[D(5)+D(2)+D(2)]
=3×D(3)﹣[D(5)+2D(2)]
=3×(2a﹣b)﹣[a+c+2×1]
=6a﹣3b﹣a﹣c﹣2
=5a﹣3b﹣c﹣2,
23.解:(1)(x+2)(3x+1)(5x﹣3)所得多项式的一次项系数为:
1×1×(﹣3)+2×3×(﹣3)+2×1×5
=﹣3﹣18+10
=﹣11;
(2)(x2+x+1)(x2﹣3x+a)(2x﹣1)所得多项式一次项系数为:
1×a×(﹣1)+1×(﹣3)×(﹣1)+1×a×2
=﹣a+3+2a
=a+3,
∵多项式不含一次项,
∴a+3=0,
解得:a=﹣3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
