人教版八年级数学上册 第12章 全等三角形 单元测试卷(含解析)
文档属性
| 名称 | 人教版八年级数学上册 第12章 全等三角形 单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 744.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览


文档简介
第12章《全等三角形》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同;
B.图形全等,只与形状,大小有关,而与它们的位置无关;
C.全等图形的面积相等,面积相等的两个图形是全等图形;
D.全等三角形的对应边相等,对应角相等.
2.(3分)已知图中的两个三角形全等,则的度数是( )
A. B. C. D.
3.如图,将两根钢条的中点O连在一起,使可以绕着点O自由旋转,则的长等于内槽宽,那么判定的理由是( )
A. B. C. D.
4.根据下列条件,能画出唯一△ABC的是( )
A.AB=4,BC=5,AC=1 B.AB=5,BC=4,∠A=40°
C.∠A=60°,∠B=50°,AB=5 D.∠C=90°,AB=8
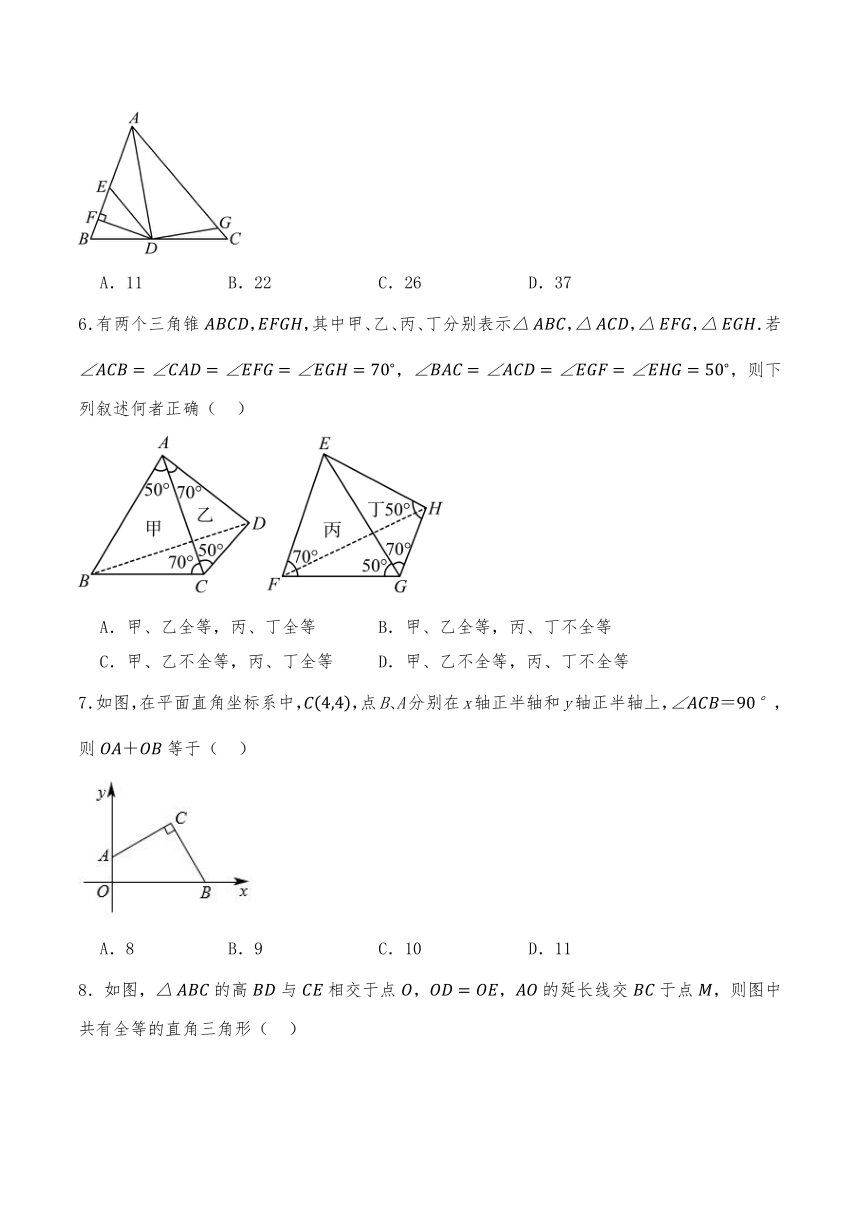
5.如图,是的角平分线,,垂足为,,和的面积分别为48和26,则的面积为( )
A.11 B.22 C.26 D.37
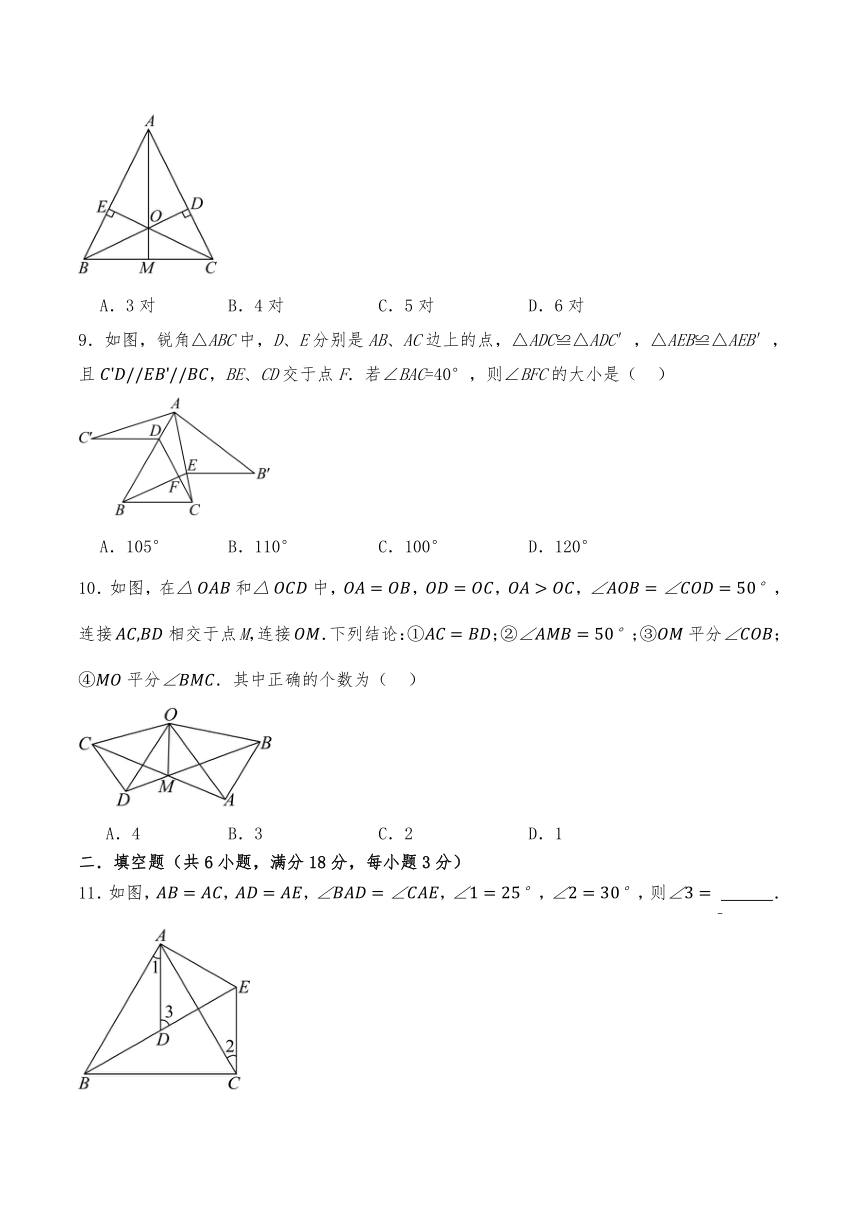
6.有两个三角锥,,其中甲、乙、丙、丁分别表示,,,.若,,则下列叙述何者正确( )
A.甲、乙全等,丙、丁全等 B.甲、乙全等,丙、丁不全等
C.甲、乙不全等,丙、丁全等 D.甲、乙不全等,丙、丁不全等
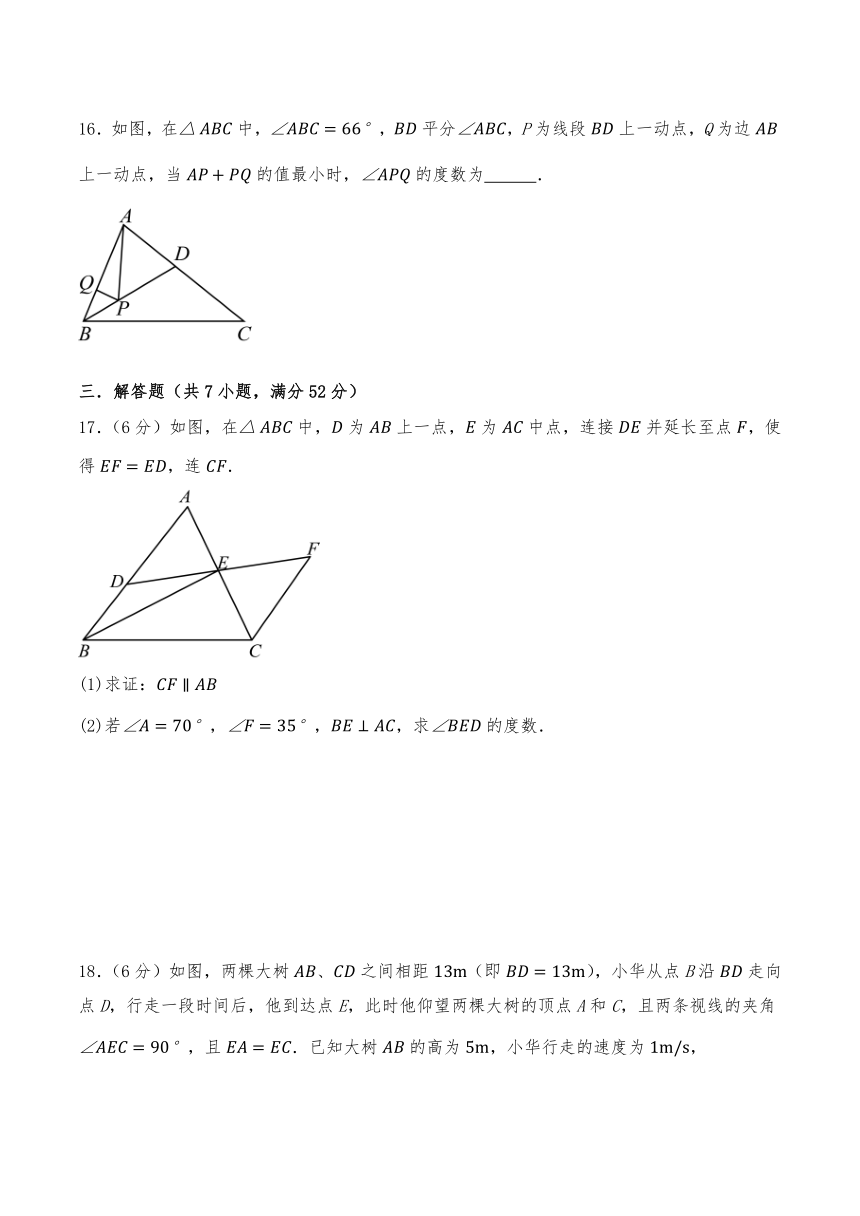
7.如图,在平面直角坐标系中,,点B、A分别在x轴正半轴和y轴正半轴上,,则等于( )
A.8 B.9 C.10 D.11
8.如图,的高与相交于点,,的延长线交于点,则图中共有全等的直角三角形( )
A.3对 B.4对 C.5对 D.6对
9.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
10.如图,在和中,,,,,连接相交于点M,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( )
A.4 B.3 C.2 D.1
二.填空题(共6小题,满分18分,每小题3分)
11.如图,,,,,,则 .
12.如图,在中,,的平分线交于点O,点O到边的距离为3,且的周长为20,则的面积为 .
13.如图,已知在和中,点B,E,C,F在同一条直线上,,.请你添加一个条件 ,使得.
14.在如图所示的3×3网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是 .
15.如图,在中,,D是的中点.点P在线段上以的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动,它们运动的时间为,设点Q的运动速度为,若使得与全等,则x的值为 .
16.如图,在中,,平分,P为线段上一动点,Q为边上一动点,当的值最小时,的度数为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在中,为上一点,为中点,连接并延长至点,使得,连.
(1)求证:
(2)若,,,求的度数.
18.(6分)如图,两棵大树、之间相距(即),小华从点B沿走向点D,行走一段时间后,他到达点E,此时他仰望两棵大树的顶点A和C,且两条视线的夹角,且.已知大树的高为,小华行走的速度为,
(1)求证:;
(2)求小华从点B走到点E的时间.
19.(8分)下面是某数学兴趣小组在项目学习课上的方案策划书,请仔细阅读,并完成相应的任务.
项目课题 探究用全等三角形解决“不用直接测量,得到高度”的问题
问题提出 墙上有一点A,在无法直接测量的情况下,如何得到点A的高度?
项目图纸
解决过程 ①标记测试直杆的底端点,测量的长度.②找一根长度大于的直杆,使直杆斜靠在墙上,且顶端与点重合;③使直杆顶端缓慢下滑,直到;④记下直杆与地面的夹角;
项目数据 …
任务:
(1)由于项目记录员粗心,记录排乱了“解决过程”,正确的顺序应是 ;
A.②→③→①→④
B.③→④→①→②
C.①→②→④→③
D.②→④→③→①
(2)若,则 ;
(3)请你说明他们作法的正确性.
20.(8分)在的高、交于点,.
(1)如图1,求证:;
(2)如图1,求的度数;
(3)如图2,延长到点,过点作的垂线交的延长线于点,当时,探究线段、、的数量关系,并证明你的结论.
21.(8分)如图所示,在中,平分,点为线段上的一个动点,交的延长线于点E.若,,求的度数.
解:(在以下解答过程的空白处填上适当的内容)
∵(已知),
( ),
∴( ),
.
∵平分(已知),
∴( ),
.
∴( ),
.
∵(已知),
∴( ).
在直角三角形中,
∵( ),
∴.
22.(8分)阅读下列材料,完成相应任务.
数学活动课上,老师提出了如下问题:
如图1,已知中,是边上的中线.求证:
智慧小组的证法如下:
证明:如图2,延长至E,使,
∵是边上的中线,
∴,
在△BDE和△CDA中,,
∴△BDE≌△ CDA(依据1),
∴,
在中,(依据2),
∴.
(1)任务一:上述证明过程中的“依据1”和“依据2”分别是指:
依据1: ;依据2: .
【归纳总结】
上述方法是通过延长中线,使,构造了一对全等三角形,将,,转化到一个三角形中,进而解决问题,这种方法叫做“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.
(2)任务二:如图3,,,则的取值范围是 ;
A.; B. ; C.
(3)任务三:利用“倍长中线法”,解决下列问题.
如图4,中,,D为中点,求证:.
23.(8分)【问题背景】
如图,在中,,,是的角平分线,它们相交于点.
【初步探究】(1)如图1,连接,求证:点在的平分线上;
【深入探究】(2)如图2,延长交于点,过点作于点于点,并连接,试判断与的大小关系;
【拓展延伸】(3)如图3,延长交于点,连接交于点,过点作于点,于点,请问和有何数量关系?
答案
一.选择题
1.C
【分析】直接利用全等三角形的定义“能够完全重合的两个三角形叫做全等三角形”与性质“全等三角形的对应边相等,对应角相等”即可得.
【详解】解:A、如果两个图形全等,那么它们的形状和大小一定相同,选项说法正确,不符合题意;
B、图形全等,只与形状,大小有关,而与它们的位置无关,选项说法正确,不符合题意;
C、全等图形的面积相等,但面积相等的两个图形不一定是全等图形;选项说法错误,符合题意;
D、全等三角形的对应边相等,对应角相等,选项说法正确,不符合题意;
故选C.
2.D
【分析】本题考查全等三角形的知识.解题时要认准对应关系.全等图形要根据已知的对应边去找对应角,并运用“全等三角形对应角相等”即可得答案.
【详解】解:图中的两个三角形全等
与,与分别是对应边,那么它们的夹角就是对应角
故选:D.
3.B
【分析】由已知O是的中点,再加上对顶角相等即可证明,利用证明全等.本题考查了三角形全等的判定方法,认真观察图形,选择合适的方法是解此题的关键.
【详解】解:∵将两根钢条的中点O连在一起,
∴,
在和中,
,
∴ ,
故选:B.
4.C
【分析】要满足唯一画出△ABC,就要求选项给出的条件符合三角形全等的判定方法,不符合判定方法的画出的图形不一样,也就是三角形不唯一,而各选项中只有C选项符合ASA,是满足题目要求的,于是答案可得
【详解】A、因为AB+ AC= BC,所以这三边不能构成三角形,故本选项不符合题意;
B、根据AB=5,BC=4,∠A=40°不能画出唯一三角形,如图所示△ABD和△ABC,故本选项不符合题意;
C、根据∠A=60°,∠B=50°,AB=5,符合全等三角形的判定定理ASA,即能画出唯一三角形,故本选项正确;
D、只有一个角和一个边无法根据此作出一个唯一的三角形,故本选项不符合题意;
故选:C
根据题意得,
5.A
【分析】本题考查的是角平分线的性质、全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.作于,根据角平分线的性质得到,证明,,根据题意列方程,解方程即可.
【详解】解:如图,作于,
是的角平分线,,,
,
在和中,
,
,
同理,,
设的面积为,由题意得,
,
解得,
即的面积为11,
故选:A
6.B
【分析】根据题意即是判断甲、乙是否全等,丙丁是否全等.运用判定定理解答.
【详解】解:,,为公共边,
,即甲、乙全等;
中,,即,
虽,,
不全等于,即丙、丁不全等.
综上所述甲、乙全等,丙、丁不全等,B正确,
故选:B.
7.A
【分析】过C作轴于M,轴于N,推出证,推出,求出,代入求出即可.
【详解】解:过C作轴于M,轴于N,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴
.
故选:A.
8.D
【分析】本题主要考查了直角三角形全等的判定方法,判定两个直角三角形全等的一般方法有:.熟练掌握运用全等三角形的判定方法是解题关键.
,,利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【详解】解:,.理由如下:
在与中,,
,
∴,
∴,
在与中,
∴,
∴,
∴,即,
∵,
∴.
在与中,,
,
∴.
在与中,,
,
∴.
在与中,
,
∴.
在与中,,
∴.
故选:D
9.C
【分析】延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′,再求出∠C′+∠AHC′即可解决问题.
【详解】解:如图延长C′D交AB′于H.
∵△AEB≌△AEB′,
∴∠ABE=∠AB′E,
∵C′H∥EB′,
∴∠AHC′=∠AB′E,
∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,
∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:C.
10.B
【分析】由SAS证明得出,①正确;由全等三角形的性质得出,由三角形的外角性质得:,得出,②正确;作,如图所示:则,由AAS证明,得出,由角平分线的判定方法得出平分,④正确;由,得出当时,才平分,假设,则,由平分得出,推出,得,而,所以,而,故③错误;即可得出结论.
【详解】解:,
,即,
在和中,
,
∴,
,①正确;
∴,
由三角形的外角性质得:,
,②正确;
作于,于,如图2所示:
则,
在和中,
,
,
,
∴平分,④正确;
∵,
∴当时,才平分,
假设,
∵,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∵,
∴,
与矛盾,
∴③错误;
正确的①②④;
故选:B.
二.填空题
11.
【分析】本题考查了全等三角形的判定与性质、三角形外角的定义及性质,证明得出,再由三角形外角的定义及性质计算即可得出答案.
【详解】解:在和中,
,
∴,
∴,
∵,
∴,
故答案为:.
12.30
【分析】本题考查角平分线的性质、三角形的面积公式,熟练掌握角平分线的性质是解答的关键.过O作于M,于N,连接,利用角平分线的性质求得,然后利用求解即可.
【详解】解:过O作于M,于N,连接,
∵点O到边的距离为3,
∴,
∵的周长为20,
∴
∵,的平分线交于点O,,,
∴,
∴
,
故答案为:30.
13.(答案不唯一)
【分析】本题考查三角形全等的性质和判定方法,判定两个三角形全等的一般方法有:、(在直角三角形中).判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
点在同一条直线上,且,即在和中,已经有两边对应相等,根据判定两个三角形全等的方法:,所以可添加条件为.
【详解】解:.
以下证明添加条件为时,.
,
,
,
,
在和中,
∴.
故答案为:.
14.4
【分析】本题考查全等三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
根据全等三角形的判定画出图形,即可判断.
【详解】解:如图,观察图象可知满足条件的三角形有4个.
由图可得,所有格点三角形的个数是4,
故答案为:4.
15.2或
【分析】本题考查全等三角形的对应边相等的性质,根据对应角分情况讨论是本题的关键.
用表示出相关线段,再根据全等三角形对应边相等,分①、是对应边,②与 是对应边两种情况讨论即可.
【详解】解:∵,点为的中点,
,
设点、的运动时间为,则,,
①当时,
,
解得:,
则,
故点的运动速度为:;
②当时,
∵,
∴,
∴,
故点的运动速度为;
故答案为:2或.
16.
【分析】在上截取,连接,证明得出,从而证明当点A、P、E在同一直线上,且时, 的值最小,再根据三角形的内角和即可求出结果
【详解】解:在上截取,连接,如图所示:
平分,
,
在和中,
,
,
,,
,
∴当点A、P、E在同一直线上,且,的值最小,即的值最小,
∴当点A、P、E在同一直线上,且时,,
,
,
∴
,
故答案为:.
三.解答题
17.(1)证明:∵为中点,
∴,
在和中,
,
∴,
∴,
∴.
(2)∵,,
∴,
∵,
∴,
∴.
18.(1)证明:∵,
∴,
∵,
∴,
∴,
在和中
∵,
∴;
(2)解:由(1)可知,,
∴,
∵,
∴,
∴小华走的时间是.
19.(1)正确的顺序应是:
②找一根长度大于的直杆,使直杆斜靠在墙上,且顶端与点重合;
④记下直杆与地面的夹角;
③使直杆顶端缓慢下滑,直到;
①标记测试直杆的底端点,测量的长度.
故答案为:;
(2)在和中,
,
,
,
,
,
;
故答案为:;
(3)证明:由(2)知,在和中,
,
,
.
即测量的长度,就等于的长度,即点的高度.
20.(1)证明:的高、交于点,如图1所示:
,,
,,
,
(2)解:在和中,
,
,
,
为等腰直角三角形,
;
(3)解:、、的数量关系是:,证明如下:
在上截取,连接,如图2所示:
是的高,,
,,
在和中,
,
,
,,
由(2)可知:,即,
,
,
即,
在和中,
,
,
,
.
21.解:(已知),
(三角形内角和等于180°),
(等式的性质),
.
∵平分(已知),
∴(角平分线的定义),
,
(三角形的一个外角等于和它不相邻的两个内角的和),
,
(已知),
(垂直的定义),
在直角三角形中,
(直角三角形的两锐角互余),
.
22.(1)解:依据1:两边和它们的夹角分别相等的两个三角形全等(或“边角边”或“”);
依据2:三角形两边的和大于第三边;
故答案为:两边和它们的夹角分别相等的两个三角形全等;三角形任意两边的和大于第三边.
(2)
解:如图,延长至点,使,连接.
是的中线,
,
在与中,
,
,
,
在中,,
即,
.
故选:C.
(3)证明:如图4,延长至F,使连接,
是的中点,
∴,
又
∴ ,
,,
∵,
∴,
,
即,
又∵,
∴ ,
∴,
∴.
23.(1)证明:如图,过点作的垂线段,分别交于点,
,是的角平分线,
,
点在的角平分线上(到角两边距离相等的点,在这个角的角平分线上);
(2),理由如下:
如图,过点作的垂线段,交的延长线于点,
是的角平分线,,
,
,
,
是的平分线,
,
,
,
,
;
(3)解:如图,过点作的垂线段,交于点,过点作于点于点,
根据(2)中原理可得,
是的平分线,
,
,
平分,,,
.
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同;
B.图形全等,只与形状,大小有关,而与它们的位置无关;
C.全等图形的面积相等,面积相等的两个图形是全等图形;
D.全等三角形的对应边相等,对应角相等.
2.(3分)已知图中的两个三角形全等,则的度数是( )
A. B. C. D.
3.如图,将两根钢条的中点O连在一起,使可以绕着点O自由旋转,则的长等于内槽宽,那么判定的理由是( )
A. B. C. D.
4.根据下列条件,能画出唯一△ABC的是( )
A.AB=4,BC=5,AC=1 B.AB=5,BC=4,∠A=40°
C.∠A=60°,∠B=50°,AB=5 D.∠C=90°,AB=8
5.如图,是的角平分线,,垂足为,,和的面积分别为48和26,则的面积为( )
A.11 B.22 C.26 D.37
6.有两个三角锥,,其中甲、乙、丙、丁分别表示,,,.若,,则下列叙述何者正确( )
A.甲、乙全等,丙、丁全等 B.甲、乙全等,丙、丁不全等
C.甲、乙不全等,丙、丁全等 D.甲、乙不全等,丙、丁不全等
7.如图,在平面直角坐标系中,,点B、A分别在x轴正半轴和y轴正半轴上,,则等于( )
A.8 B.9 C.10 D.11
8.如图,的高与相交于点,,的延长线交于点,则图中共有全等的直角三角形( )
A.3对 B.4对 C.5对 D.6对
9.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
10.如图,在和中,,,,,连接相交于点M,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( )
A.4 B.3 C.2 D.1
二.填空题(共6小题,满分18分,每小题3分)
11.如图,,,,,,则 .
12.如图,在中,,的平分线交于点O,点O到边的距离为3,且的周长为20,则的面积为 .
13.如图,已知在和中,点B,E,C,F在同一条直线上,,.请你添加一个条件 ,使得.
14.在如图所示的3×3网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是 .
15.如图,在中,,D是的中点.点P在线段上以的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动,它们运动的时间为,设点Q的运动速度为,若使得与全等,则x的值为 .
16.如图,在中,,平分,P为线段上一动点,Q为边上一动点,当的值最小时,的度数为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在中,为上一点,为中点,连接并延长至点,使得,连.
(1)求证:
(2)若,,,求的度数.
18.(6分)如图,两棵大树、之间相距(即),小华从点B沿走向点D,行走一段时间后,他到达点E,此时他仰望两棵大树的顶点A和C,且两条视线的夹角,且.已知大树的高为,小华行走的速度为,
(1)求证:;
(2)求小华从点B走到点E的时间.
19.(8分)下面是某数学兴趣小组在项目学习课上的方案策划书,请仔细阅读,并完成相应的任务.
项目课题 探究用全等三角形解决“不用直接测量,得到高度”的问题
问题提出 墙上有一点A,在无法直接测量的情况下,如何得到点A的高度?
项目图纸
解决过程 ①标记测试直杆的底端点,测量的长度.②找一根长度大于的直杆,使直杆斜靠在墙上,且顶端与点重合;③使直杆顶端缓慢下滑,直到;④记下直杆与地面的夹角;
项目数据 …
任务:
(1)由于项目记录员粗心,记录排乱了“解决过程”,正确的顺序应是 ;
A.②→③→①→④
B.③→④→①→②
C.①→②→④→③
D.②→④→③→①
(2)若,则 ;
(3)请你说明他们作法的正确性.
20.(8分)在的高、交于点,.
(1)如图1,求证:;
(2)如图1,求的度数;
(3)如图2,延长到点,过点作的垂线交的延长线于点,当时,探究线段、、的数量关系,并证明你的结论.
21.(8分)如图所示,在中,平分,点为线段上的一个动点,交的延长线于点E.若,,求的度数.
解:(在以下解答过程的空白处填上适当的内容)
∵(已知),
( ),
∴( ),
.
∵平分(已知),
∴( ),
.
∴( ),
.
∵(已知),
∴( ).
在直角三角形中,
∵( ),
∴.
22.(8分)阅读下列材料,完成相应任务.
数学活动课上,老师提出了如下问题:
如图1,已知中,是边上的中线.求证:
智慧小组的证法如下:
证明:如图2,延长至E,使,
∵是边上的中线,
∴,
在△BDE和△CDA中,,
∴△BDE≌△ CDA(依据1),
∴,
在中,(依据2),
∴.
(1)任务一:上述证明过程中的“依据1”和“依据2”分别是指:
依据1: ;依据2: .
【归纳总结】
上述方法是通过延长中线,使,构造了一对全等三角形,将,,转化到一个三角形中,进而解决问题,这种方法叫做“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.
(2)任务二:如图3,,,则的取值范围是 ;
A.; B. ; C.
(3)任务三:利用“倍长中线法”,解决下列问题.
如图4,中,,D为中点,求证:.
23.(8分)【问题背景】
如图,在中,,,是的角平分线,它们相交于点.
【初步探究】(1)如图1,连接,求证:点在的平分线上;
【深入探究】(2)如图2,延长交于点,过点作于点于点,并连接,试判断与的大小关系;
【拓展延伸】(3)如图3,延长交于点,连接交于点,过点作于点,于点,请问和有何数量关系?
答案
一.选择题
1.C
【分析】直接利用全等三角形的定义“能够完全重合的两个三角形叫做全等三角形”与性质“全等三角形的对应边相等,对应角相等”即可得.
【详解】解:A、如果两个图形全等,那么它们的形状和大小一定相同,选项说法正确,不符合题意;
B、图形全等,只与形状,大小有关,而与它们的位置无关,选项说法正确,不符合题意;
C、全等图形的面积相等,但面积相等的两个图形不一定是全等图形;选项说法错误,符合题意;
D、全等三角形的对应边相等,对应角相等,选项说法正确,不符合题意;
故选C.
2.D
【分析】本题考查全等三角形的知识.解题时要认准对应关系.全等图形要根据已知的对应边去找对应角,并运用“全等三角形对应角相等”即可得答案.
【详解】解:图中的两个三角形全等
与,与分别是对应边,那么它们的夹角就是对应角
故选:D.
3.B
【分析】由已知O是的中点,再加上对顶角相等即可证明,利用证明全等.本题考查了三角形全等的判定方法,认真观察图形,选择合适的方法是解此题的关键.
【详解】解:∵将两根钢条的中点O连在一起,
∴,
在和中,
,
∴ ,
故选:B.
4.C
【分析】要满足唯一画出△ABC,就要求选项给出的条件符合三角形全等的判定方法,不符合判定方法的画出的图形不一样,也就是三角形不唯一,而各选项中只有C选项符合ASA,是满足题目要求的,于是答案可得
【详解】A、因为AB+ AC= BC,所以这三边不能构成三角形,故本选项不符合题意;
B、根据AB=5,BC=4,∠A=40°不能画出唯一三角形,如图所示△ABD和△ABC,故本选项不符合题意;
C、根据∠A=60°,∠B=50°,AB=5,符合全等三角形的判定定理ASA,即能画出唯一三角形,故本选项正确;
D、只有一个角和一个边无法根据此作出一个唯一的三角形,故本选项不符合题意;
故选:C
根据题意得,
5.A
【分析】本题考查的是角平分线的性质、全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.作于,根据角平分线的性质得到,证明,,根据题意列方程,解方程即可.
【详解】解:如图,作于,
是的角平分线,,,
,
在和中,
,
,
同理,,
设的面积为,由题意得,
,
解得,
即的面积为11,
故选:A
6.B
【分析】根据题意即是判断甲、乙是否全等,丙丁是否全等.运用判定定理解答.
【详解】解:,,为公共边,
,即甲、乙全等;
中,,即,
虽,,
不全等于,即丙、丁不全等.
综上所述甲、乙全等,丙、丁不全等,B正确,
故选:B.
7.A
【分析】过C作轴于M,轴于N,推出证,推出,求出,代入求出即可.
【详解】解:过C作轴于M,轴于N,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴
.
故选:A.
8.D
【分析】本题主要考查了直角三角形全等的判定方法,判定两个直角三角形全等的一般方法有:.熟练掌握运用全等三角形的判定方法是解题关键.
,,利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【详解】解:,.理由如下:
在与中,,
,
∴,
∴,
在与中,
∴,
∴,
∴,即,
∵,
∴.
在与中,,
,
∴.
在与中,,
,
∴.
在与中,
,
∴.
在与中,,
∴.
故选:D
9.C
【分析】延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′,再求出∠C′+∠AHC′即可解决问题.
【详解】解:如图延长C′D交AB′于H.
∵△AEB≌△AEB′,
∴∠ABE=∠AB′E,
∵C′H∥EB′,
∴∠AHC′=∠AB′E,
∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,
∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:C.
10.B
【分析】由SAS证明得出,①正确;由全等三角形的性质得出,由三角形的外角性质得:,得出,②正确;作,如图所示:则,由AAS证明,得出,由角平分线的判定方法得出平分,④正确;由,得出当时,才平分,假设,则,由平分得出,推出,得,而,所以,而,故③错误;即可得出结论.
【详解】解:,
,即,
在和中,
,
∴,
,①正确;
∴,
由三角形的外角性质得:,
,②正确;
作于,于,如图2所示:
则,
在和中,
,
,
,
∴平分,④正确;
∵,
∴当时,才平分,
假设,
∵,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∵,
∴,
与矛盾,
∴③错误;
正确的①②④;
故选:B.
二.填空题
11.
【分析】本题考查了全等三角形的判定与性质、三角形外角的定义及性质,证明得出,再由三角形外角的定义及性质计算即可得出答案.
【详解】解:在和中,
,
∴,
∴,
∵,
∴,
故答案为:.
12.30
【分析】本题考查角平分线的性质、三角形的面积公式,熟练掌握角平分线的性质是解答的关键.过O作于M,于N,连接,利用角平分线的性质求得,然后利用求解即可.
【详解】解:过O作于M,于N,连接,
∵点O到边的距离为3,
∴,
∵的周长为20,
∴
∵,的平分线交于点O,,,
∴,
∴
,
故答案为:30.
13.(答案不唯一)
【分析】本题考查三角形全等的性质和判定方法,判定两个三角形全等的一般方法有:、(在直角三角形中).判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
点在同一条直线上,且,即在和中,已经有两边对应相等,根据判定两个三角形全等的方法:,所以可添加条件为.
【详解】解:.
以下证明添加条件为时,.
,
,
,
,
在和中,
∴.
故答案为:.
14.4
【分析】本题考查全等三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
根据全等三角形的判定画出图形,即可判断.
【详解】解:如图,观察图象可知满足条件的三角形有4个.
由图可得,所有格点三角形的个数是4,
故答案为:4.
15.2或
【分析】本题考查全等三角形的对应边相等的性质,根据对应角分情况讨论是本题的关键.
用表示出相关线段,再根据全等三角形对应边相等,分①、是对应边,②与 是对应边两种情况讨论即可.
【详解】解:∵,点为的中点,
,
设点、的运动时间为,则,,
①当时,
,
解得:,
则,
故点的运动速度为:;
②当时,
∵,
∴,
∴,
故点的运动速度为;
故答案为:2或.
16.
【分析】在上截取,连接,证明得出,从而证明当点A、P、E在同一直线上,且时, 的值最小,再根据三角形的内角和即可求出结果
【详解】解:在上截取,连接,如图所示:
平分,
,
在和中,
,
,
,,
,
∴当点A、P、E在同一直线上,且,的值最小,即的值最小,
∴当点A、P、E在同一直线上,且时,,
,
,
∴
,
故答案为:.
三.解答题
17.(1)证明:∵为中点,
∴,
在和中,
,
∴,
∴,
∴.
(2)∵,,
∴,
∵,
∴,
∴.
18.(1)证明:∵,
∴,
∵,
∴,
∴,
在和中
∵,
∴;
(2)解:由(1)可知,,
∴,
∵,
∴,
∴小华走的时间是.
19.(1)正确的顺序应是:
②找一根长度大于的直杆,使直杆斜靠在墙上,且顶端与点重合;
④记下直杆与地面的夹角;
③使直杆顶端缓慢下滑,直到;
①标记测试直杆的底端点,测量的长度.
故答案为:;
(2)在和中,
,
,
,
,
,
;
故答案为:;
(3)证明:由(2)知,在和中,
,
,
.
即测量的长度,就等于的长度,即点的高度.
20.(1)证明:的高、交于点,如图1所示:
,,
,,
,
(2)解:在和中,
,
,
,
为等腰直角三角形,
;
(3)解:、、的数量关系是:,证明如下:
在上截取,连接,如图2所示:
是的高,,
,,
在和中,
,
,
,,
由(2)可知:,即,
,
,
即,
在和中,
,
,
,
.
21.解:(已知),
(三角形内角和等于180°),
(等式的性质),
.
∵平分(已知),
∴(角平分线的定义),
,
(三角形的一个外角等于和它不相邻的两个内角的和),
,
(已知),
(垂直的定义),
在直角三角形中,
(直角三角形的两锐角互余),
.
22.(1)解:依据1:两边和它们的夹角分别相等的两个三角形全等(或“边角边”或“”);
依据2:三角形两边的和大于第三边;
故答案为:两边和它们的夹角分别相等的两个三角形全等;三角形任意两边的和大于第三边.
(2)
解:如图,延长至点,使,连接.
是的中线,
,
在与中,
,
,
,
在中,,
即,
.
故选:C.
(3)证明:如图4,延长至F,使连接,
是的中点,
∴,
又
∴ ,
,,
∵,
∴,
,
即,
又∵,
∴ ,
∴,
∴.
23.(1)证明:如图,过点作的垂线段,分别交于点,
,是的角平分线,
,
点在的角平分线上(到角两边距离相等的点,在这个角的角平分线上);
(2),理由如下:
如图,过点作的垂线段,交的延长线于点,
是的角平分线,,
,
,
,
是的平分线,
,
,
,
,
;
(3)解:如图,过点作的垂线段,交于点,过点作于点于点,
根据(2)中原理可得,
是的平分线,
,
,
平分,,,
.
