北师大九下2.5.2二次函数与一元二次方程(2)
文档属性
| 名称 | 北师大九下2.5.2二次函数与一元二次方程(2) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 11:20:33 | ||
图片预览








文档简介
(共25张PPT)
第二章 二次函数
2.5.2二次函数与一元二次方程(2)
北师大版 数学 九年级 下册
学习目标
1、利用二次函数的图象求一元二次方程近似解.
2、经历探索用二次函数图象求解一元二次方程近似解的过程,体会用二次函数函数图象求一元二次方程解的方法.
情景导入
我们知道:
我们能否利用二次函数的图象
x
y
O
x1
x2
y=ax2+bx+c
是一元二次方程ax2+bx+c=0 (a≠0)的解
那么交点的横坐标。
估计一元二次方程的解呢?
抛物线y=ax2+bx+c (a≠0)与x轴如果相交,
核心知识点一:
利用图象法求一元二次方程的近似根
你能利用二次函数的图象估计一元二次方程 x2+2x-10=0 的根吗?
如图是函数 y=x2+2x-10 的图象.
(1)由图象知,方程 x2+2x-10=0 有 个根,
一个根在 和 之间,另一个根
在 和 之间(填两个整数).
2
-4
-5
2
3
探索新知
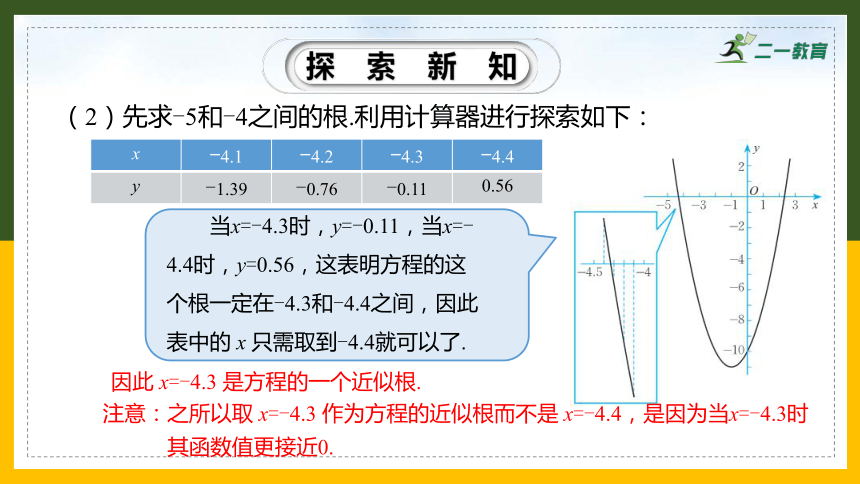
因此 x=-4.3 是方程的一个近似根.
(2)先求-5和-4之间的根.利用计算器进行探索如下:
x -4.1 -4.2 -4.3 -4.4
y -1.39 -0.76 -0.11 0.56
当x=-4.3时,y=-0.11,当x=-4.4时,y=0.56,这表明方程的这个根一定在-4.3和-4.4之间,因此表中的 x 只需取到-4.4就可以了.
注意:之所以取 x=-4.3 作为方程的近似根而不是 x=-4.4,是因为当x=-4.3时
其函数值更接近0.
探索新知
(3)再求 2 和 3 之间的根.利用计算器探索如下:
x 2.1 2.2 2.3 2.4
y -1.39 -0.76 -0.11 0.56
因此 x=2.3是方程的另一个近似根.
探索新知
(1)画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在哪两个整数之间;
(3)列表,在两个整数之间取值,并用计算器算出对应的y值,当x由x1变到x2,对应的y值出现y1>0,y2<0(或y1<0,y2>0)且|y1|≠|y2|时,x1,x2中必有一个是方程的近似根,再比较|y1|和|y2|,若|y1|<|y2|,则x1是方程的近似根;若|y1|>|y2|,则x2是方程的近似根.
利用二次函数的图象求一元二次方程的近似根的一般步骤:
探索新知
做一做:(1)请利用图像求一元二次方程 x2+2x-10=3 的近似根.
方程 x2+2x-10=3 可变形为 x2+2x-13=0.
如图是函数 y=x2+2x-13 的图象.由图象可知方程x2+2x-13=0 有两个根,一个在 -5 和 -4 之间,一个在 2 和 3 之间.
探索新知
x 2.9 2.8 2.7 2.6
y 1.21 0.44 -0.31 -1.04
x -4.9 -4.8 -4.7 -4.6
y 1.21 0.44 -0.31 -1.04
因此 x=-4.7和 x=2.7 是方程的近似根.
做一做:(1)请利用图像求一元二次方程 x2+2x-10=3 的近似根.
探索新知
(2)请利用图 6 求一元二次方程 x2+2x-10=3 的近似根.
如图是函数 y=x2+2x-10 的图象.由图象可知方程x2+2x-10=0 有两个根,一个在 -5 和-4 之间,一个在 2 和 3 之间.
探索新知
x 2.9 2.8 2.7 2.6
y 4.21 3.44 2.69 1.96
x -4.9 -4.8 -4.7 -4.6
y 4.21 3.44 2.69 1.96
因此 x=-4.7和 x=2.7 是方程的近似根.
(2)请利用图 6 求一元二次方程 x2+2x-10=3 的近似根.
探索新知
归纳总结
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值);
利用图象法求一元二次方程的近似根
(3)确定方程ax2+bx+c=0的近似根
(两个函数值异号)
探索新知
解:先把方程化成x2=-2x+3.如图,
在同一直角坐标系中分别画出函数
y=x2和y=-2x+3的图象,
则方程x2+2x-3=0的解为x=-3或x=1.
练一练:利用函数的图象,求方程x2+2x-3=0的根.
探索新知
(1)将ax2+bx+c=0化为ax2=-bx-c的形式;
(2)在同一坐标系中画出y=ax2与y=-bx-c的图象;
(3)观察图象:两图象的公共点情况即为方程的根的情况,如有公共点,则公共点的横坐标即为ax2+bx+c=0的根.
利用图象交点法求一元二次方程的根的步骤:
归纳总结
探索新知
当堂检测
1.下表给出了二次函数 中, , 的一些
对应值,则可以估计一元二次方程 的一个
近似解(精确到 )为( )
… 2 2.1 2.2 2.3 2.4 …
… 0.24 0.89 1.56 …
B
A. B.2.2 C. D.
当堂检测
2.如图,以点 为顶点的二次函数
的图象与 轴正半轴交
于 点,则一元二次方程
的负实数根的取值范围是( )
C
A. B.
C. D.
当堂检测
3.已知二次函数 的图象如图所示,
则不等式 的解集是( )
D
A. 或 B.
C. D. 或
当堂检测
4.在同一平面直角坐标系中,抛物线
与直线 的图象如图所示,
那么不等式 的解集是( )
B
A. B.
C. D. 或
当堂检测
5.二次函数 的图象如图所示,对称
轴为直线 .若关于 的一元二次方程
为实数 在 的范
围内有解,则 的取值范围是( )
C
A. B.
C. D.
当堂检测
6.某班数学兴趣小组对函数 的图象和性质进行了探
究,探究过程如下,请补充完整.
(1)自变量 的取值范围是全体实数, 与 的几组对应值列表如下:
… 0 0.5 1 1.5 2 2.5 3 …
… 3 0 0.75 1 0.75 0 1.25 3 …
其中, _____.
1.25
当堂检测
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
解:函数图象如图所示.
当堂检测
(3)进一步探究函数图象并解决问题:
①方程 有___个实数根;
4
【解析】 由函数图象,知函数 的图象与直线 有4个交点,所以方程 有4个实数根.
当堂检测
②在(2)中的平面直角坐标系中画出直线 ,根据图象,方程
的一个正数根约为____.(精确到 )
0.4
【解析】 如图,由图象和表格可知方程 的一个正数
根约为0.4.
图象法求方程ax +bx+c=0的近似根的步骤:
①作出函数y=ax +bx+c的图象;
②利用图象找出函数图象与x轴的交点,
③根据交点的横坐标,
按近似要求写出方程ax +bx+c=0的近似根
感谢收看
第二章 二次函数
2.5.2二次函数与一元二次方程(2)
北师大版 数学 九年级 下册
学习目标
1、利用二次函数的图象求一元二次方程近似解.
2、经历探索用二次函数图象求解一元二次方程近似解的过程,体会用二次函数函数图象求一元二次方程解的方法.
情景导入
我们知道:
我们能否利用二次函数的图象
x
y
O
x1
x2
y=ax2+bx+c
是一元二次方程ax2+bx+c=0 (a≠0)的解
那么交点的横坐标。
估计一元二次方程的解呢?
抛物线y=ax2+bx+c (a≠0)与x轴如果相交,
核心知识点一:
利用图象法求一元二次方程的近似根
你能利用二次函数的图象估计一元二次方程 x2+2x-10=0 的根吗?
如图是函数 y=x2+2x-10 的图象.
(1)由图象知,方程 x2+2x-10=0 有 个根,
一个根在 和 之间,另一个根
在 和 之间(填两个整数).
2
-4
-5
2
3
探索新知
因此 x=-4.3 是方程的一个近似根.
(2)先求-5和-4之间的根.利用计算器进行探索如下:
x -4.1 -4.2 -4.3 -4.4
y -1.39 -0.76 -0.11 0.56
当x=-4.3时,y=-0.11,当x=-4.4时,y=0.56,这表明方程的这个根一定在-4.3和-4.4之间,因此表中的 x 只需取到-4.4就可以了.
注意:之所以取 x=-4.3 作为方程的近似根而不是 x=-4.4,是因为当x=-4.3时
其函数值更接近0.
探索新知
(3)再求 2 和 3 之间的根.利用计算器探索如下:
x 2.1 2.2 2.3 2.4
y -1.39 -0.76 -0.11 0.56
因此 x=2.3是方程的另一个近似根.
探索新知
(1)画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在哪两个整数之间;
(3)列表,在两个整数之间取值,并用计算器算出对应的y值,当x由x1变到x2,对应的y值出现y1>0,y2<0(或y1<0,y2>0)且|y1|≠|y2|时,x1,x2中必有一个是方程的近似根,再比较|y1|和|y2|,若|y1|<|y2|,则x1是方程的近似根;若|y1|>|y2|,则x2是方程的近似根.
利用二次函数的图象求一元二次方程的近似根的一般步骤:
探索新知
做一做:(1)请利用图像求一元二次方程 x2+2x-10=3 的近似根.
方程 x2+2x-10=3 可变形为 x2+2x-13=0.
如图是函数 y=x2+2x-13 的图象.由图象可知方程x2+2x-13=0 有两个根,一个在 -5 和 -4 之间,一个在 2 和 3 之间.
探索新知
x 2.9 2.8 2.7 2.6
y 1.21 0.44 -0.31 -1.04
x -4.9 -4.8 -4.7 -4.6
y 1.21 0.44 -0.31 -1.04
因此 x=-4.7和 x=2.7 是方程的近似根.
做一做:(1)请利用图像求一元二次方程 x2+2x-10=3 的近似根.
探索新知
(2)请利用图 6 求一元二次方程 x2+2x-10=3 的近似根.
如图是函数 y=x2+2x-10 的图象.由图象可知方程x2+2x-10=0 有两个根,一个在 -5 和-4 之间,一个在 2 和 3 之间.
探索新知
x 2.9 2.8 2.7 2.6
y 4.21 3.44 2.69 1.96
x -4.9 -4.8 -4.7 -4.6
y 4.21 3.44 2.69 1.96
因此 x=-4.7和 x=2.7 是方程的近似根.
(2)请利用图 6 求一元二次方程 x2+2x-10=3 的近似根.
探索新知
归纳总结
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值);
利用图象法求一元二次方程的近似根
(3)确定方程ax2+bx+c=0的近似根
(两个函数值异号)
探索新知
解:先把方程化成x2=-2x+3.如图,
在同一直角坐标系中分别画出函数
y=x2和y=-2x+3的图象,
则方程x2+2x-3=0的解为x=-3或x=1.
练一练:利用函数的图象,求方程x2+2x-3=0的根.
探索新知
(1)将ax2+bx+c=0化为ax2=-bx-c的形式;
(2)在同一坐标系中画出y=ax2与y=-bx-c的图象;
(3)观察图象:两图象的公共点情况即为方程的根的情况,如有公共点,则公共点的横坐标即为ax2+bx+c=0的根.
利用图象交点法求一元二次方程的根的步骤:
归纳总结
探索新知
当堂检测
1.下表给出了二次函数 中, , 的一些
对应值,则可以估计一元二次方程 的一个
近似解(精确到 )为( )
… 2 2.1 2.2 2.3 2.4 …
… 0.24 0.89 1.56 …
B
A. B.2.2 C. D.
当堂检测
2.如图,以点 为顶点的二次函数
的图象与 轴正半轴交
于 点,则一元二次方程
的负实数根的取值范围是( )
C
A. B.
C. D.
当堂检测
3.已知二次函数 的图象如图所示,
则不等式 的解集是( )
D
A. 或 B.
C. D. 或
当堂检测
4.在同一平面直角坐标系中,抛物线
与直线 的图象如图所示,
那么不等式 的解集是( )
B
A. B.
C. D. 或
当堂检测
5.二次函数 的图象如图所示,对称
轴为直线 .若关于 的一元二次方程
为实数 在 的范
围内有解,则 的取值范围是( )
C
A. B.
C. D.
当堂检测
6.某班数学兴趣小组对函数 的图象和性质进行了探
究,探究过程如下,请补充完整.
(1)自变量 的取值范围是全体实数, 与 的几组对应值列表如下:
… 0 0.5 1 1.5 2 2.5 3 …
… 3 0 0.75 1 0.75 0 1.25 3 …
其中, _____.
1.25
当堂检测
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
解:函数图象如图所示.
当堂检测
(3)进一步探究函数图象并解决问题:
①方程 有___个实数根;
4
【解析】 由函数图象,知函数 的图象与直线 有4个交点,所以方程 有4个实数根.
当堂检测
②在(2)中的平面直角坐标系中画出直线 ,根据图象,方程
的一个正数根约为____.(精确到 )
0.4
【解析】 如图,由图象和表格可知方程 的一个正数
根约为0.4.
图象法求方程ax +bx+c=0的近似根的步骤:
①作出函数y=ax +bx+c的图象;
②利用图象找出函数图象与x轴的交点,
③根据交点的横坐标,
按近似要求写出方程ax +bx+c=0的近似根
感谢收看
