北师大九下2.2.2二次函数的图像和性质(2)
文档属性
| 名称 | 北师大九下2.2.2二次函数的图像和性质(2) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 11:20:33 | ||
图片预览





文档简介
(共25张PPT)
第二章 二次函数
2.2.2二次函数的图像和性质(2)
北师大版 数学 九年级 下册
学习目标
1.会画二次函数y=ax2和y=ax2+c的图象.
2.掌握二次函数y=ax2和y=ax2+c的性质并会应用.
3.比较函数y=ax2与y=ax2+c的联系.
情景导入
图象
开口 方向
对称性 顶点 最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
情景导入
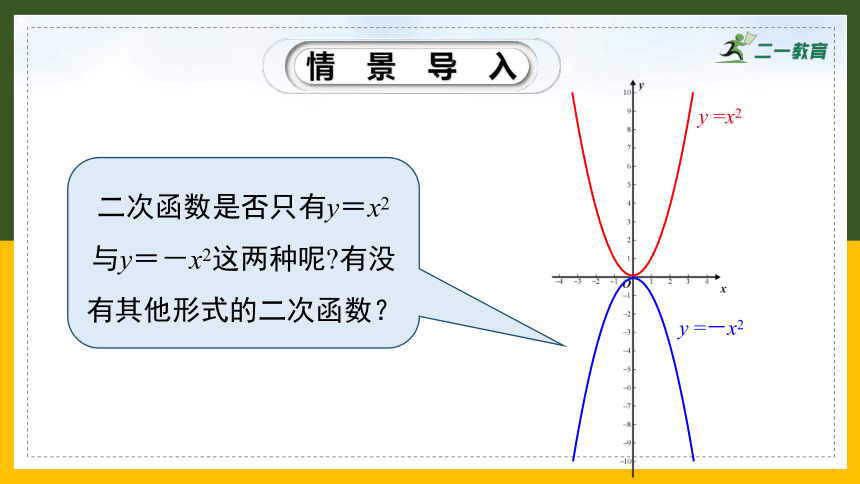
y =-x2
y =x2
二次函数是否只有y=x2与y=-x2这两种呢 有没有其他形式的二次函数?
核心知识点一:
二次函数y=ax2的图象与性质
画二次函数 的图象.
1.列表:完成下表:
x
y
坐标
-2
8
-1
2
0
0
1
2
2
8
(-2,8)
(-1,2)
(0,0)
(1,2)
(2,8)
···
···
···
···
探索新知
2.描点:在直角坐标系中描点.
3.连线:用光滑的曲线顺次连接各点,便得到函数 的图象.
2
4
-2
-4
0
3
6
9
x
y
探索新知
2
4
-2
-4
0
3
6
9
x
y
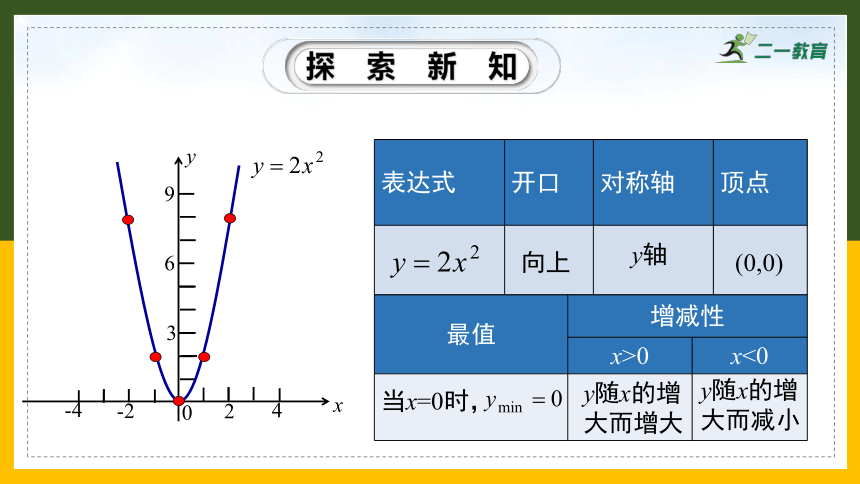
表达式 开口 对称轴 顶点
向上
y轴
(0,0)
最值 增减性 x>0 x<0
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
探索新知
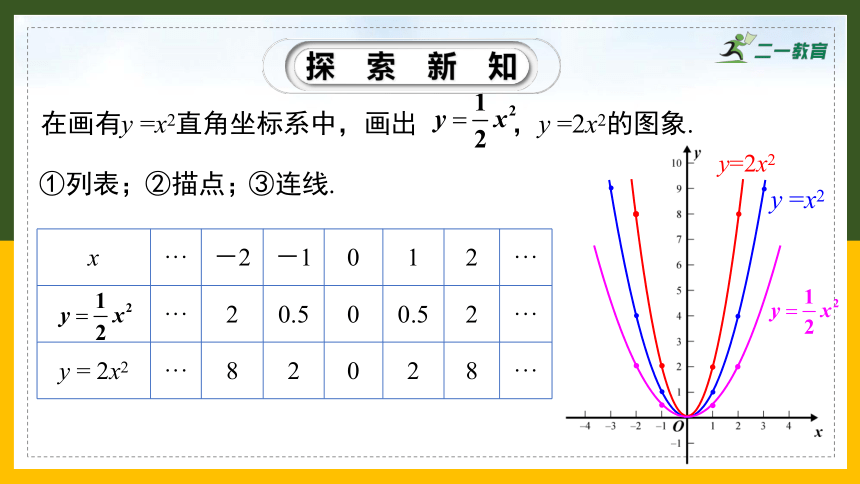
x ··· -2 -1 0 1 2 ···
··· 2 0.5 0 0.5 2 ···
y = 2x2 ··· 8 2 0 2 8 ···
在画有y =x2直角坐标系中,画出 ,y =2x2的图象.
y =x2
①列表;
②描点;
③连线.
y=2x2
探索新知
y =x2
y=2x2
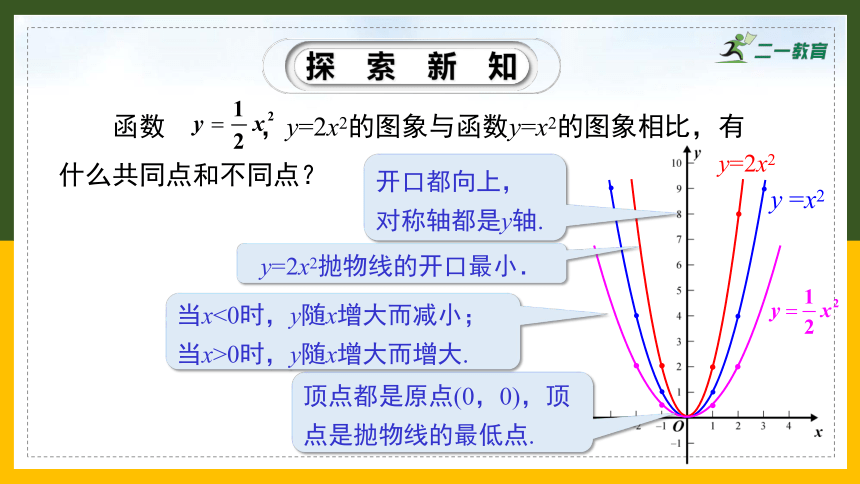
函数 ,y=2x2的图象与函数y=x2的图象相比,有什么共同点和不同点?
开口都向上,
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最低点.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
y=2x2抛物线的开口最小.
探索新知
在画有 y =-x2的直角坐标系中,画出 的图象.
y =-x2
x ··· -2 -1 0 1 2 ···
··· -2 -0.5 0 -0.5 -2 ···
y = -2x2 ··· -8 -2 0 -2 -8 ···
①列表;
②描点;
③连线.
y=-2x2
探索新知
y =-x2
y=-2x2
函数 ,y=-2x2的图象与函数y=-x2的图象相比,有什么共同点和不同点?
开口都向下;
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最高点;
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
a值越小,抛物线的开口越小.
探索新知
归纳总结
y=ax2 (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增 减 性
最值
向上
向下
(0,0)
(0,0)
y轴 (x=0)
y轴 (x=0)
在对称轴的左侧,
y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,
y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来,|a|越大,抛物线的开口就越小.
探索新知
核心知识点二:
二次函数y=ax2+c的图象与性质
画二次函数 的图象,你是怎样画的?
2
4
-2
-4
0
3
6
9
x
y
1.二次函数 的图象与二次函数 的图象有什么关系?
2.它是轴对称图形吗?它的开口方向、对称轴、顶点坐标分别是什么呢?
3.二次函数 的图象又是什么样的呢?
形状相同,位置不同
探索新知
2
4
-2
-4
0
3
6
9
x
y
图象
图象
图象
向上平移一个单位长度
向下平移一个单位长度
探索新知
2
4
-2
-4
o
3
6
9
x
y
表达式 开口 对称轴 顶点 最值 增减性 x>0 x<0
向上
y轴
(0,0)
y随x的增
大而增大
y随x的增
大而减小
当x=0时,
向上
y轴
(0,1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
向上
y轴
(0,-1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
探索新知
二次函数 与 的图象的关系:
二次函数 的图象可以由 的图象平移得到:
当c > 0时,向上平移c个单位长度得到.
当c < 0时,向下平移 |c|个单位长度得到.
开口 对称轴 顶点 最值 增减性 x>0 x<0
a>0
a<0
向上
y轴
(0,c)
y随x的增大而增大
y随x的增大而减小
当x=0时,
向下
y轴
(0,c)
当x=0时,
y随x的增大而减小
y随x的增大而增大
归纳总结
探索新知
当堂检测
1.二次函数y=-x2-4的图象经过的象限为( )
A.第一、第四象限 B.第二、第四象限
C.第三、第四象限 D.第一、第三、第四象限
2.若A(-6,y1),B(-3,y2),C(1,y3)为二次函数y=2x2-1图象上的三点,则y1,y2,y3的大小关系是( )
A.y3C.y3C
A
当堂检测
3.已知抛物线y=(a-1)x2+2的顶点是此抛物线的最低点,那么a的取值范围是( )
A.a≠0 B.a≠1
C.a>1 D.a<1
4.二次函数y=12-ax2的图象经过点A(2,8),B(-3,n),则a的值为
,n的值为 .
C
1
3
当堂检测
5.将抛物线y=x2-1向上平移2个单位长度,所得的抛物线的函数表达式是( )
A.y=x2-3
B.y=x2+1
C.y=2x2-1
D.y=(x+2)2-1
6.若抛物线y=ax2沿y轴向下平移2个单位长度就能与y=-2x2+c的图象完全重合,则c的值为 .
B
-2
当堂检测
7.已知二次函数y=ax2与y=-2x2+c.
(1)若这两个函数图象的形状及开口方向相同,则a的值为 ;
(2)二次函数y=-2x2+c中x,y的几组对应值如下表:
-2
x -2 1 5
y m n p
表中m,n,p的大小关系为 (用“<”连接).
p当堂检测
(0,3)
10
2≤y≤4
当堂检测
解:如图所示.
当堂检测
12.将抛物线y=mx2+n向下平移6个单位长度,得到抛物线y=-x2+3,设原抛物线的顶点为P,且原抛物线与x轴相交于点A,B,且点A在点B的左
侧,求△PAB的面积.
二次函数y=ax2+c(a≠0)的图象和性质
图象
性质
与y=ax2的关系
开口方向由a的符号决定;
c决定顶点位置;
对称轴是y轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
c正向上;
c负向下.
感谢收看
第二章 二次函数
2.2.2二次函数的图像和性质(2)
北师大版 数学 九年级 下册
学习目标
1.会画二次函数y=ax2和y=ax2+c的图象.
2.掌握二次函数y=ax2和y=ax2+c的性质并会应用.
3.比较函数y=ax2与y=ax2+c的联系.
情景导入
图象
开口 方向
对称性 顶点 最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
情景导入
y =-x2
y =x2
二次函数是否只有y=x2与y=-x2这两种呢 有没有其他形式的二次函数?
核心知识点一:
二次函数y=ax2的图象与性质
画二次函数 的图象.
1.列表:完成下表:
x
y
坐标
-2
8
-1
2
0
0
1
2
2
8
(-2,8)
(-1,2)
(0,0)
(1,2)
(2,8)
···
···
···
···
探索新知
2.描点:在直角坐标系中描点.
3.连线:用光滑的曲线顺次连接各点,便得到函数 的图象.
2
4
-2
-4
0
3
6
9
x
y
探索新知
2
4
-2
-4
0
3
6
9
x
y
表达式 开口 对称轴 顶点
向上
y轴
(0,0)
最值 增减性 x>0 x<0
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
探索新知
x ··· -2 -1 0 1 2 ···
··· 2 0.5 0 0.5 2 ···
y = 2x2 ··· 8 2 0 2 8 ···
在画有y =x2直角坐标系中,画出 ,y =2x2的图象.
y =x2
①列表;
②描点;
③连线.
y=2x2
探索新知
y =x2
y=2x2
函数 ,y=2x2的图象与函数y=x2的图象相比,有什么共同点和不同点?
开口都向上,
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最低点.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
y=2x2抛物线的开口最小.
探索新知
在画有 y =-x2的直角坐标系中,画出 的图象.
y =-x2
x ··· -2 -1 0 1 2 ···
··· -2 -0.5 0 -0.5 -2 ···
y = -2x2 ··· -8 -2 0 -2 -8 ···
①列表;
②描点;
③连线.
y=-2x2
探索新知
y =-x2
y=-2x2
函数 ,y=-2x2的图象与函数y=-x2的图象相比,有什么共同点和不同点?
开口都向下;
对称轴都是y轴.
顶点都是原点(0,0),顶点是抛物线的最高点;
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
a值越小,抛物线的开口越小.
探索新知
归纳总结
y=ax2 (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增 减 性
最值
向上
向下
(0,0)
(0,0)
y轴 (x=0)
y轴 (x=0)
在对称轴的左侧,
y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,
y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来,|a|越大,抛物线的开口就越小.
探索新知
核心知识点二:
二次函数y=ax2+c的图象与性质
画二次函数 的图象,你是怎样画的?
2
4
-2
-4
0
3
6
9
x
y
1.二次函数 的图象与二次函数 的图象有什么关系?
2.它是轴对称图形吗?它的开口方向、对称轴、顶点坐标分别是什么呢?
3.二次函数 的图象又是什么样的呢?
形状相同,位置不同
探索新知
2
4
-2
-4
0
3
6
9
x
y
图象
图象
图象
向上平移一个单位长度
向下平移一个单位长度
探索新知
2
4
-2
-4
o
3
6
9
x
y
表达式 开口 对称轴 顶点 最值 增减性 x>0 x<0
向上
y轴
(0,0)
y随x的增
大而增大
y随x的增
大而减小
当x=0时,
向上
y轴
(0,1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
向上
y轴
(0,-1)
当x=0时,
y随x的增
大而增大
y随x的增
大而减小
探索新知
二次函数 与 的图象的关系:
二次函数 的图象可以由 的图象平移得到:
当c > 0时,向上平移c个单位长度得到.
当c < 0时,向下平移 |c|个单位长度得到.
开口 对称轴 顶点 最值 增减性 x>0 x<0
a>0
a<0
向上
y轴
(0,c)
y随x的增大而增大
y随x的增大而减小
当x=0时,
向下
y轴
(0,c)
当x=0时,
y随x的增大而减小
y随x的增大而增大
归纳总结
探索新知
当堂检测
1.二次函数y=-x2-4的图象经过的象限为( )
A.第一、第四象限 B.第二、第四象限
C.第三、第四象限 D.第一、第三、第四象限
2.若A(-6,y1),B(-3,y2),C(1,y3)为二次函数y=2x2-1图象上的三点,则y1,y2,y3的大小关系是( )
A.y3
A
当堂检测
3.已知抛物线y=(a-1)x2+2的顶点是此抛物线的最低点,那么a的取值范围是( )
A.a≠0 B.a≠1
C.a>1 D.a<1
4.二次函数y=12-ax2的图象经过点A(2,8),B(-3,n),则a的值为
,n的值为 .
C
1
3
当堂检测
5.将抛物线y=x2-1向上平移2个单位长度,所得的抛物线的函数表达式是( )
A.y=x2-3
B.y=x2+1
C.y=2x2-1
D.y=(x+2)2-1
6.若抛物线y=ax2沿y轴向下平移2个单位长度就能与y=-2x2+c的图象完全重合,则c的值为 .
B
-2
当堂检测
7.已知二次函数y=ax2与y=-2x2+c.
(1)若这两个函数图象的形状及开口方向相同,则a的值为 ;
(2)二次函数y=-2x2+c中x,y的几组对应值如下表:
-2
x -2 1 5
y m n p
表中m,n,p的大小关系为 (用“<”连接).
p
(0,3)
10
2≤y≤4
当堂检测
解:如图所示.
当堂检测
12.将抛物线y=mx2+n向下平移6个单位长度,得到抛物线y=-x2+3,设原抛物线的顶点为P,且原抛物线与x轴相交于点A,B,且点A在点B的左
侧,求△PAB的面积.
二次函数y=ax2+c(a≠0)的图象和性质
图象
性质
与y=ax2的关系
开口方向由a的符号决定;
c决定顶点位置;
对称轴是y轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
c正向上;
c负向下.
感谢收看
