第19章矩形、菱形与正方形单元测试A卷(含解析)
文档属性
| 名称 | 第19章矩形、菱形与正方形单元测试A卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 745.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 22:14:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第19章矩形、菱形与正方形单元测试A卷
华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列说法正确的是( )
A.平行四边形对角线相等 B.矩形的对角线互相垂直
C.菱形的四个角都相等 D.正方形的对角线互相平分
2.如图,已知菱形ABCD的周长为8,∠A=60°,则对角线BD的长是( )
A.1 B. C.2 D.2
3.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG的值为( )
A. B. C. D.
6.如图,边长为4cm的正方形ABCD的对角线相交于点O,点O又是正方形EFGO的一个顶点,则两个正方形重叠部分的面积是( )cm2.
A.8 B.4 C.6 D.2
7.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.1.2 B.1.3 C.1.4 D.2.4
8.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;②△OEF面积的最小值是;
③至少存在一个△ECF,使得△ECF的周长是;④四边形OECF的面积是1.
所有符合题意结论的序号是( )
A.①②③ B.③④ C.①②④ D.①②③④
二、填空题
9.已知菱形的面积为24cm2,一条对角线长为6cm,则这个菱形的周长是 厘米.
10.如图:在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是 .
11.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,若∠BCE=70°,则∠EAD= .
12.如图,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
三、解答题
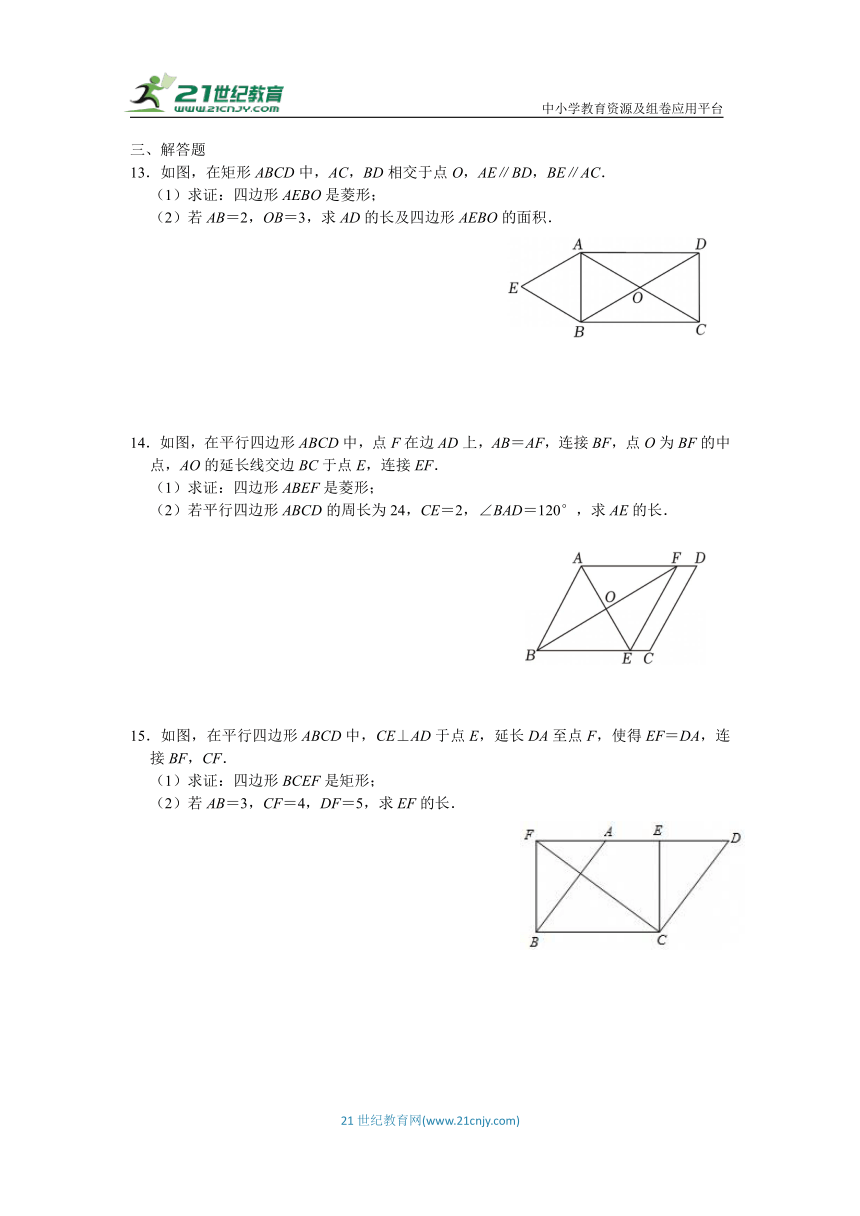
13.如图,在矩形ABCD中,AC,BD相交于点O,AE∥BD,BE∥AC.
(1)求证:四边形AEBO是菱形;
(2)若AB=2,OB=3,求AD的长及四边形AEBO的面积.
14.如图,在平行四边形ABCD中,点F在边AD上,AB=AF,连接BF,点O为BF的中点,AO的延长线交边BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若平行四边形ABCD的周长为24,CE=2,∠BAD=120°,求AE的长.
15.如图,在平行四边形ABCD中,CE⊥AD于点E,延长DA至点F,使得EF=DA,连接BF,CF.
(1)求证:四边形BCEF是矩形;
(2)若AB=3,CF=4,DF=5,求EF的长.
16.如图,直线经过矩形ABCD的对角线BD的中点O,分别与矩形的两边相交于点E、F.
(1)求证:OE=OF;
(2)若EF⊥BD,则四边形BEDF是 形,并说明理由;
(3)在(2)的条件下,若AD=8,BD=10,求△BDE的面积.
17.在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
(1)求证:∠DAE=∠ADE;
(2)求证:△AEB≌△DEC;
(3)当EB=BC时,求∠AFD的度数.
18.如图①正方形ABCD中,点E是对角线AC上任意一点,连接DE,BE.
(1)求证:DE=BE;
(2)当AE=AB时,求∠BED的度数;
(3)如图②,过点E作EF⊥DE交AB于点F,当BE=BF时,若AB.求AF的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D C C B C B A D
1.【解答】解:A、平行四边形对角线互相平分,错误;
B、矩形的对角线相等,错误;
C、菱形的四条边都相等,错误;
D、正方形的对角线互相垂直平分且相等,正确;
故选:D.
2.【解答】解:∵四边形ABCD是菱形,
∴AB=AD,
又∵∠A=60°,
∴△ABD是等边三角形,
∴BD=AB,
故选:C.
3.【解答】解:根据等腰三角形的判定定理可得,平行四边形的一组邻边相等,即可判定该平行四边形是菱形,
故A不符合题意;
根据三角形内角和定理可得,平行四边形的对角线互相垂直,即可判定该平行四边形是菱形,
故B不符合题意;
一组邻角互补,不能判定该平行四边形是菱形,
故C符合题意;
根据平行四边形的邻角互补,对角线平分一个120°的角,可得平行四边形的一组邻边相等,即可判定该平行四边形是菱形,
故D不符合题意;
故选:C.
4.【解答】解:A、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠BDC,
∵∠ABD=∠CBD,
∴∠BDC=∠CBD,
∴BC=CD,
∴四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误,不符合题意;
B、∵∠ABC=90°,
∴平行四边形ABCD是矩形,故本选项正确,符合题意;
C、∵四边形ABCD是平行四边形,
∴当AC⊥BD时四边形ABCD是菱形,故本选项错误,不符合题意;
D、根据AB=BC和平行四边形ABCD不能得出四边形ABCD是矩形,故本选项错误,不符合题意,不符合题意;
故选:B.
5.【解答】解:作CH⊥BD于点H,连接OE,
∵四边形ABCD是矩形,
∴AC=BD,OC=OAAC,OB=ODBD,
∴OC=OB,
∵∠BCD=90°,CD=AB=5,BC=AD=12,
∴BD13,
∴OC=OB13,
∵BD CHBC CD=S△BCD,
∴13CH12×5,
解得CH,
∵EF⊥AC,EG⊥BD,垂足分别为点F,G,S△COE+S△BOE=S△BOC,
∴OC EFOB EGOB CH,
∴EFEG,
∴EF+EG,
故选:C.
6.【解答】解:∵四边形ABCD是正方形,
∴OA=OB,∠OBM=∠OAH=45°,∠AOB=∠BOC=90°,
∴∠AOH=∠BOM,
在△AOH与△BOM中,
,
∴△AOH≌△BOM(ASA),
∴S△AOH=S△BOM,
∴四边形OHBM的面积等于△AOB的面积,即两个正方形重叠部分的面积等于正方形ABCD面积的,
∴两个正方形重叠部分的面积是,
故选:B.
7.【解答】解:连接AP,如图所示:
∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴PMAP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样PM也最短,
∴当AP⊥BC时,AP2.4,
∴AP最短时,AP=2.4,
∴当PM最短时,PMAP=1.2.
故选:A.
8.【解答】解:①∵四边形ABCD是正方形,AC,BD相交于点O,
∴OB=OC,∠OBC=∠OCD=45°,
在△OBE和△OCF中,
,
∴△OBE≌△OCF(SAS),
∴OE=OF,
∵∠BOE=∠COF,
∴∠EOF=∠BOC=90°,
∴△OEF是等腰直角三角形;
故①正确;
②∵当OE⊥BC时,OE最小,此时OE=OFBC=1,
∴△OEF面积的最小值是1×1,
故②正确;
③∵BE=CF,
∴CE+CF=CE+BE=BC=2,
假设存在一个△ECF,使得△ECF的周长是2,
则EF,
由①得△OEF是等腰直角三角形,
∴OE.
∵OB,OE的最小值是1,
∴存在一个△ECF,使得△ECF的周长是2.
故③正确;
④由①知:△OBE≌△OCF,
∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBCS正方形ABCD2×2=1,
故④正确;
故选:D.
二、填空题
9.【解答】解:如图所示:
∵菱形的面积等于对角线乘积的一半,AC=6cm,S菱形ABCD=24cm2,
∴BD=8cm,AO=3cm,BO=4cm,
在Rt△ABO中,AB2=AO2+BO2,
即有AB2=32+42,
解得:AB=5cm,
∴菱形的周长=4×5=20cm.
故答案为:20.
10.【解答】解:如图,连接CE,
设DE=x,则AE=8﹣x,
∵OE⊥AC,且点O是AC的中点,
∴OE是AC的垂直平分线,
∴CE=AE=8﹣x,
在Rt△CDE中,
x2+42=(8﹣x)2
解得x=3,
∴DE的长是3.
故答案为:3.
11.【解答】解:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,
∵DE=DE,
∴△AED≌△CED(SAS),
∴∠EAD=∠ECD,
又∵∠BCE=70°,
方法1:∴∠EAD=∠BAD﹣∠BCE=20°.
方法2:∴∠BEC=65°,
∵∠BEC=∠CDE+∠ECD,
即65°=45°+∠ECD,
∴∠ECD=20°,
∴∠EAD=20°.
故答案为:20°.
12.【解答】解:本图是由八个全等的直角三角形拼成的,设这个直角三角形两个直角边中较长的长度为a,较短的长度为b,即图中的AE=a,AH=b,
则,,,
∵S1+S2+S3=40,
∴(a+b)2+a2+b2+(a﹣b)2=40,
a2+b2+2ab+a2+b2+a2+b2﹣2ab=40,
3a2+3b2=40,
,
∴.
故答案是:.
三、解答题
13.【解答】(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴OA=OB,
∴四边形AEBO是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠DAB=90°,AO=CO,BO=DO,AC=BD,
∴OA=OB=OC=DO,
∵OB=3,
∴BD=6,
由勾股定理得:AD4,
∵BO=DO,
∴S△AOB=S△AODS△BADAD×AB42=2,
∵四边形AEBO是菱形,
∴AE=AO=BO=BE=3,
∴△AEB≌△BOA(SSS),
∴△AEB的面积=△AOB的面积=2,
∴四边形AEBO的面积是22=4.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠EBF,∠FAE=∠BEA,
∵O为BF的中点,
∴BO=FO,
在△AOF和△EOB中,
,
∴△AOF≌△EOB(AAS),
∴BE=FA,
∴四边形ABEF是平行四边形,
又AB=AF,
∴平行四边形ABEF是菱形;
(2)解:∵AD=BC,AF=BE,
∴DF=CE=2,
∵平行四边形ABCD的周长为24,
∴菱形ABEF的周长为:24﹣4=20,
∴AB=20÷4=5,
∵∠BAD=120°,
∴,
又 AB=BE,
∴△ABE是等边三角形,
∴AE=AB=5.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵EF=DA,
∴EF=BC,EF∥BC,
∴四边形BCEF是平行四边形,
又∵CE⊥AD,
∴∠CEF=90°,
∴平行四边形BCEF是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=3,
∵CF=4,DF=5,
∴CD2+CF2=DF2,
∴△CDF是直角三角形,∠DCF=90°,
∴△CDF的面积DF×CECF×CD,
∴CE,
由(1)得:EF=BC,四边形BCEF是矩形,
∴∠FBC=90°,BF=CE,
∴BC,
∴EF.
16.【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDO=∠FBO,
∵点O是BD的中点,
∴BO=DO,
在△BOF与△DOE中,
,
∴△BOF≌△DOE(ASA),
∴OE=OF;
(2)四边形BEDF是菱形,理由:
∵OE=OF,OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形;
故答案为:菱;
(3)∵四边形ABCD是矩形,
∴∠A=90°,
∵AD=8,BD=10,
∴,
设BE=DE=x,则AE=8﹣x,
∵AB2+AE2=BE2,
∴62+(8﹣x)2=x2,
解得:,
∴,
∵,
∴,
∴△BDE的面积.
17.【解答】(1)证明:∵ABCD为正方形,
∴∠BAD=90°,
∵点E为DF中点,
∴AE=EF=DEDF,
∴∠EAD=∠EDA;
(2)证明:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,
∵∠EAD=∠EDA,
∵∠BAE=∠BAD﹣∠EAD,∠CDE=∠ADC﹣∠EDA,
∴∠BAE=∠CDE,
在△AEB和△DEC中,
,
∴△AEB≌△DEC(SAS);
(3)解:∵△AEB≌△DEC,
∴EB=EC,
∵EB=BC,
∴EB=BC=EC,
∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=90°﹣60°=30°,
∵EB=BC=AB,
∴∠BAE(180°﹣30°)=75°,
又∵AE=EF,
∴∠AFD=∠BAE=75°.
18.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠BAE,
∵AE=AE,
∴△DAE≌△BAE(SAS),
∴DE=BE;
(2)∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
由(1)知:△DAE≌△BAE,
∴∠AED=∠AEB(180°﹣45°)135°,
∴∠BED=2∠AEB=135°;
(3)如图②,过E作EM⊥BF,
∵四边形ABCD是正方形,
∴CD=CB,∠DCE=∠BCE,
∵CE=CE,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵∠ADC=∠ABC=90°,
∴∠ADE=∠ABE,
∵DE⊥EF,
∴∠DEF=90°,
在四边形ADEF中,∠DAF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠BFE=180°,
∴∠BFE=∠EBF,
∴BE=EF,
∵BE=BF,
∴△BEF是等边三角形,
∴∠EBF=60°,
设BM=x,则MF=BM=x,EMx,
∵四边形ABCD是正方形,
∴∠BAE∠BAD=45°,
∴AM=EMx,
∵AM+BM=AB,
∴xx,
解得,x,
∴BF=2x=2,
∴AF=AB﹣BF2.
21世纪教育网(www.21cnjy.com)
第19章矩形、菱形与正方形单元测试A卷
华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列说法正确的是( )
A.平行四边形对角线相等 B.矩形的对角线互相垂直
C.菱形的四个角都相等 D.正方形的对角线互相平分
2.如图,已知菱形ABCD的周长为8,∠A=60°,则对角线BD的长是( )
A.1 B. C.2 D.2
3.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG的值为( )
A. B. C. D.
6.如图,边长为4cm的正方形ABCD的对角线相交于点O,点O又是正方形EFGO的一个顶点,则两个正方形重叠部分的面积是( )cm2.
A.8 B.4 C.6 D.2
7.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.1.2 B.1.3 C.1.4 D.2.4
8.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;②△OEF面积的最小值是;
③至少存在一个△ECF,使得△ECF的周长是;④四边形OECF的面积是1.
所有符合题意结论的序号是( )
A.①②③ B.③④ C.①②④ D.①②③④
二、填空题
9.已知菱形的面积为24cm2,一条对角线长为6cm,则这个菱形的周长是 厘米.
10.如图:在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是 .
11.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,若∠BCE=70°,则∠EAD= .
12.如图,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
三、解答题
13.如图,在矩形ABCD中,AC,BD相交于点O,AE∥BD,BE∥AC.
(1)求证:四边形AEBO是菱形;
(2)若AB=2,OB=3,求AD的长及四边形AEBO的面积.
14.如图,在平行四边形ABCD中,点F在边AD上,AB=AF,连接BF,点O为BF的中点,AO的延长线交边BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若平行四边形ABCD的周长为24,CE=2,∠BAD=120°,求AE的长.
15.如图,在平行四边形ABCD中,CE⊥AD于点E,延长DA至点F,使得EF=DA,连接BF,CF.
(1)求证:四边形BCEF是矩形;
(2)若AB=3,CF=4,DF=5,求EF的长.
16.如图,直线经过矩形ABCD的对角线BD的中点O,分别与矩形的两边相交于点E、F.
(1)求证:OE=OF;
(2)若EF⊥BD,则四边形BEDF是 形,并说明理由;
(3)在(2)的条件下,若AD=8,BD=10,求△BDE的面积.
17.在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
(1)求证:∠DAE=∠ADE;
(2)求证:△AEB≌△DEC;
(3)当EB=BC时,求∠AFD的度数.
18.如图①正方形ABCD中,点E是对角线AC上任意一点,连接DE,BE.
(1)求证:DE=BE;
(2)当AE=AB时,求∠BED的度数;
(3)如图②,过点E作EF⊥DE交AB于点F,当BE=BF时,若AB.求AF的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D C C B C B A D
1.【解答】解:A、平行四边形对角线互相平分,错误;
B、矩形的对角线相等,错误;
C、菱形的四条边都相等,错误;
D、正方形的对角线互相垂直平分且相等,正确;
故选:D.
2.【解答】解:∵四边形ABCD是菱形,
∴AB=AD,
又∵∠A=60°,
∴△ABD是等边三角形,
∴BD=AB,
故选:C.
3.【解答】解:根据等腰三角形的判定定理可得,平行四边形的一组邻边相等,即可判定该平行四边形是菱形,
故A不符合题意;
根据三角形内角和定理可得,平行四边形的对角线互相垂直,即可判定该平行四边形是菱形,
故B不符合题意;
一组邻角互补,不能判定该平行四边形是菱形,
故C符合题意;
根据平行四边形的邻角互补,对角线平分一个120°的角,可得平行四边形的一组邻边相等,即可判定该平行四边形是菱形,
故D不符合题意;
故选:C.
4.【解答】解:A、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠BDC,
∵∠ABD=∠CBD,
∴∠BDC=∠CBD,
∴BC=CD,
∴四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误,不符合题意;
B、∵∠ABC=90°,
∴平行四边形ABCD是矩形,故本选项正确,符合题意;
C、∵四边形ABCD是平行四边形,
∴当AC⊥BD时四边形ABCD是菱形,故本选项错误,不符合题意;
D、根据AB=BC和平行四边形ABCD不能得出四边形ABCD是矩形,故本选项错误,不符合题意,不符合题意;
故选:B.
5.【解答】解:作CH⊥BD于点H,连接OE,
∵四边形ABCD是矩形,
∴AC=BD,OC=OAAC,OB=ODBD,
∴OC=OB,
∵∠BCD=90°,CD=AB=5,BC=AD=12,
∴BD13,
∴OC=OB13,
∵BD CHBC CD=S△BCD,
∴13CH12×5,
解得CH,
∵EF⊥AC,EG⊥BD,垂足分别为点F,G,S△COE+S△BOE=S△BOC,
∴OC EFOB EGOB CH,
∴EFEG,
∴EF+EG,
故选:C.
6.【解答】解:∵四边形ABCD是正方形,
∴OA=OB,∠OBM=∠OAH=45°,∠AOB=∠BOC=90°,
∴∠AOH=∠BOM,
在△AOH与△BOM中,
,
∴△AOH≌△BOM(ASA),
∴S△AOH=S△BOM,
∴四边形OHBM的面积等于△AOB的面积,即两个正方形重叠部分的面积等于正方形ABCD面积的,
∴两个正方形重叠部分的面积是,
故选:B.
7.【解答】解:连接AP,如图所示:
∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴PMAP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样PM也最短,
∴当AP⊥BC时,AP2.4,
∴AP最短时,AP=2.4,
∴当PM最短时,PMAP=1.2.
故选:A.
8.【解答】解:①∵四边形ABCD是正方形,AC,BD相交于点O,
∴OB=OC,∠OBC=∠OCD=45°,
在△OBE和△OCF中,
,
∴△OBE≌△OCF(SAS),
∴OE=OF,
∵∠BOE=∠COF,
∴∠EOF=∠BOC=90°,
∴△OEF是等腰直角三角形;
故①正确;
②∵当OE⊥BC时,OE最小,此时OE=OFBC=1,
∴△OEF面积的最小值是1×1,
故②正确;
③∵BE=CF,
∴CE+CF=CE+BE=BC=2,
假设存在一个△ECF,使得△ECF的周长是2,
则EF,
由①得△OEF是等腰直角三角形,
∴OE.
∵OB,OE的最小值是1,
∴存在一个△ECF,使得△ECF的周长是2.
故③正确;
④由①知:△OBE≌△OCF,
∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBCS正方形ABCD2×2=1,
故④正确;
故选:D.
二、填空题
9.【解答】解:如图所示:
∵菱形的面积等于对角线乘积的一半,AC=6cm,S菱形ABCD=24cm2,
∴BD=8cm,AO=3cm,BO=4cm,
在Rt△ABO中,AB2=AO2+BO2,
即有AB2=32+42,
解得:AB=5cm,
∴菱形的周长=4×5=20cm.
故答案为:20.
10.【解答】解:如图,连接CE,
设DE=x,则AE=8﹣x,
∵OE⊥AC,且点O是AC的中点,
∴OE是AC的垂直平分线,
∴CE=AE=8﹣x,
在Rt△CDE中,
x2+42=(8﹣x)2
解得x=3,
∴DE的长是3.
故答案为:3.
11.【解答】解:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,
∵DE=DE,
∴△AED≌△CED(SAS),
∴∠EAD=∠ECD,
又∵∠BCE=70°,
方法1:∴∠EAD=∠BAD﹣∠BCE=20°.
方法2:∴∠BEC=65°,
∵∠BEC=∠CDE+∠ECD,
即65°=45°+∠ECD,
∴∠ECD=20°,
∴∠EAD=20°.
故答案为:20°.
12.【解答】解:本图是由八个全等的直角三角形拼成的,设这个直角三角形两个直角边中较长的长度为a,较短的长度为b,即图中的AE=a,AH=b,
则,,,
∵S1+S2+S3=40,
∴(a+b)2+a2+b2+(a﹣b)2=40,
a2+b2+2ab+a2+b2+a2+b2﹣2ab=40,
3a2+3b2=40,
,
∴.
故答案是:.
三、解答题
13.【解答】(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴OA=OB,
∴四边形AEBO是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠DAB=90°,AO=CO,BO=DO,AC=BD,
∴OA=OB=OC=DO,
∵OB=3,
∴BD=6,
由勾股定理得:AD4,
∵BO=DO,
∴S△AOB=S△AODS△BADAD×AB42=2,
∵四边形AEBO是菱形,
∴AE=AO=BO=BE=3,
∴△AEB≌△BOA(SSS),
∴△AEB的面积=△AOB的面积=2,
∴四边形AEBO的面积是22=4.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠EBF,∠FAE=∠BEA,
∵O为BF的中点,
∴BO=FO,
在△AOF和△EOB中,
,
∴△AOF≌△EOB(AAS),
∴BE=FA,
∴四边形ABEF是平行四边形,
又AB=AF,
∴平行四边形ABEF是菱形;
(2)解:∵AD=BC,AF=BE,
∴DF=CE=2,
∵平行四边形ABCD的周长为24,
∴菱形ABEF的周长为:24﹣4=20,
∴AB=20÷4=5,
∵∠BAD=120°,
∴,
又 AB=BE,
∴△ABE是等边三角形,
∴AE=AB=5.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵EF=DA,
∴EF=BC,EF∥BC,
∴四边形BCEF是平行四边形,
又∵CE⊥AD,
∴∠CEF=90°,
∴平行四边形BCEF是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=3,
∵CF=4,DF=5,
∴CD2+CF2=DF2,
∴△CDF是直角三角形,∠DCF=90°,
∴△CDF的面积DF×CECF×CD,
∴CE,
由(1)得:EF=BC,四边形BCEF是矩形,
∴∠FBC=90°,BF=CE,
∴BC,
∴EF.
16.【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDO=∠FBO,
∵点O是BD的中点,
∴BO=DO,
在△BOF与△DOE中,
,
∴△BOF≌△DOE(ASA),
∴OE=OF;
(2)四边形BEDF是菱形,理由:
∵OE=OF,OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形;
故答案为:菱;
(3)∵四边形ABCD是矩形,
∴∠A=90°,
∵AD=8,BD=10,
∴,
设BE=DE=x,则AE=8﹣x,
∵AB2+AE2=BE2,
∴62+(8﹣x)2=x2,
解得:,
∴,
∵,
∴,
∴△BDE的面积.
17.【解答】(1)证明:∵ABCD为正方形,
∴∠BAD=90°,
∵点E为DF中点,
∴AE=EF=DEDF,
∴∠EAD=∠EDA;
(2)证明:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,
∵∠EAD=∠EDA,
∵∠BAE=∠BAD﹣∠EAD,∠CDE=∠ADC﹣∠EDA,
∴∠BAE=∠CDE,
在△AEB和△DEC中,
,
∴△AEB≌△DEC(SAS);
(3)解:∵△AEB≌△DEC,
∴EB=EC,
∵EB=BC,
∴EB=BC=EC,
∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=90°﹣60°=30°,
∵EB=BC=AB,
∴∠BAE(180°﹣30°)=75°,
又∵AE=EF,
∴∠AFD=∠BAE=75°.
18.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠BAE,
∵AE=AE,
∴△DAE≌△BAE(SAS),
∴DE=BE;
(2)∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
由(1)知:△DAE≌△BAE,
∴∠AED=∠AEB(180°﹣45°)135°,
∴∠BED=2∠AEB=135°;
(3)如图②,过E作EM⊥BF,
∵四边形ABCD是正方形,
∴CD=CB,∠DCE=∠BCE,
∵CE=CE,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵∠ADC=∠ABC=90°,
∴∠ADE=∠ABE,
∵DE⊥EF,
∴∠DEF=90°,
在四边形ADEF中,∠DAF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠BFE=180°,
∴∠BFE=∠EBF,
∴BE=EF,
∵BE=BF,
∴△BEF是等边三角形,
∴∠EBF=60°,
设BM=x,则MF=BM=x,EMx,
∵四边形ABCD是正方形,
∴∠BAE∠BAD=45°,
∴AM=EMx,
∵AM+BM=AB,
∴xx,
解得,x,
∴BF=2x=2,
∴AF=AB﹣BF2.
21世纪教育网(www.21cnjy.com)
