第二十章数据的分析 考点分类练(含答案)2024-2025学年数学人教版八年级下册
文档属性
| 名称 | 第二十章数据的分析 考点分类练(含答案)2024-2025学年数学人教版八年级下册 | 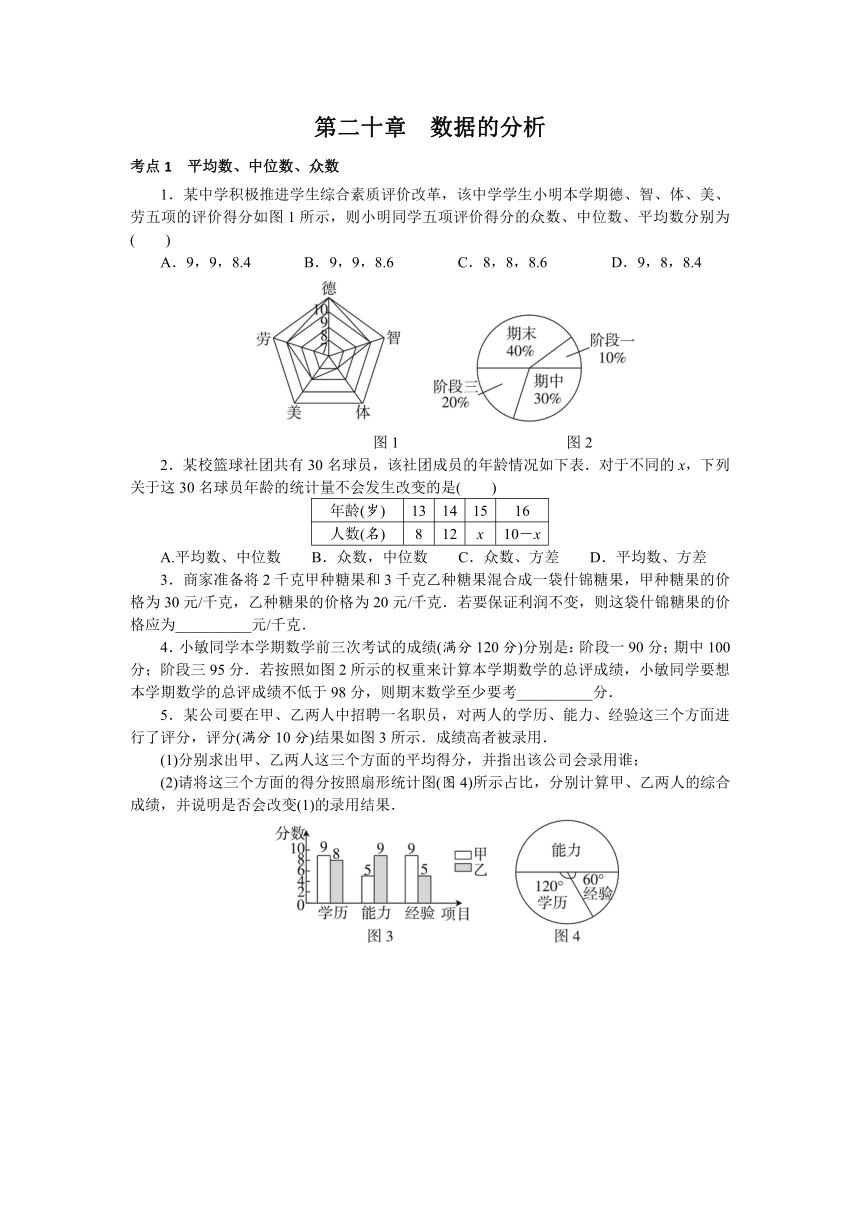 | |
| 格式 | docx | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 16:16:34 | ||
图片预览


文档简介
第二十章 数据的分析
考点1 平均数、中位数、众数
1.某中学积极推进学生综合素质评价改革,该中学学生小明本学期德、智、体、美、劳五项的评价得分如图1所示,则小明同学五项评价得分的众数、中位数、平均数分别为( )
A.9,9,8.4 B.9,9,8.6 C.8,8,8.6 D.9,8,8.4
图1 图2
2.某校篮球社团共有30名球员,该社团成员的年龄情况如下表.对于不同的x,下列关于这30名球员年龄的统计量不会发生改变的是( )
年龄(岁) 13 14 15 16
人数(名) 8 12 x 10-x
A.平均数、中位数 B.众数,中位数 C.众数、方差 D.平均数、方差
3.商家准备将2千克甲种糖果和3千克乙种糖果混合成一袋什锦糖果,甲种糖果的价格为30元/千克,乙种糖果的价格为20元/千克.若要保证利润不变,则这袋什锦糖果的价格应为__________元/千克.
4.小敏同学本学期数学前三次考试的成绩(满分120分)分别是:阶段一90分;期中100分;阶段三95分.若按照如图2所示的权重来计算本学期数学的总评成绩,小敏同学要想本学期数学的总评成绩不低于98分,则期末数学至少要考__________分.
5.某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三个方面进行了评分,评分(满分10分)结果如图3所示.成绩高者被录用.
(1)分别求出甲、乙两人这三个方面的平均得分,并指出该公司会录用谁;
(2)请将这三个方面的得分按照扇形统计图(图4)所示占比,分别计算甲、乙两人的综合成绩,并说明是否会改变(1)的录用结果.
6.为了进一步推进学校安全教育,切实增强广大学生的安全防范意识和自护自救能力,某校举行了安全知识网络竞赛活动,满分为100分.为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级抽取了20名参赛学生的成绩.已知抽到的八年级的竞赛成绩(单位:分)如下:80,95,60,80,75,60,95,65,75,70,80,75,85,65,90,70,75,80,85,80.注:分数在80分以上(不含80分)为优秀.
为了便于分析数据,统计员对八年级的数据进行了整理,得到下表:
成绩等级 成绩(分) 学生数
D级 60≤x≤70 a
C级 70<x≤80 9
B级 80<x≤90 b
A级 90<x≤100 2
八、九年级所抽取学生的竞赛成绩的平均数、中位数、优秀率如下表:
年级 平均数 中位数 优秀率
八年级 77 c 25%
九年级 78.5 82.5 50%
(1)填空:a=__________,b=__________,c=__________;
(2)八年级学生小明和九年级学生小亮的此次竞赛成绩都是80分,则这两名同学在各自年级的排名__________更靠前;(填“小明”或“小亮”)
(3)若该校九年级共有700名学生参加此次竞赛,请估计九年级有多少名学生的竞赛成绩达到优秀.
考点2 方差
7.已知一组数据x1,x2,x3,x4,x5的平均数是4,方差是3,另一组数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的平均数是__________,方差是__________.
8.甲、乙两人在相同条件下各射击10次,每次射击的成绩情况如图5所示.
图5
根据图示信息,整理分析数据如下表:
平均数 中位数 众数 命中9环及9环以上的次数
甲 7 7 a 1
乙 b c 7,8,9 d
(1)填空:a=________,b=________,c=________,d=________.
(2)计算甲、乙两人这10次射击成绩的方差.
(3)请从下列不同的角度对甲、乙两人这10次射击的成绩进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩更好些);
③从图5中两人射击命中环数的走势看(分析谁更有潜力).
9.药物研发机构为对比研究某种药物对甲、乙两种流感(简称甲流、乙流)的疗效,需要检测患者体内的药物浓度m和病毒载量n两个指标,该机构分别在服用该药物的甲流患者和乙流患者中,各随机选取15人作为调查对象,将收集到的数据整理后,绘制成如图6所示的统计图.
根据以上信息,回答下列问题:
(1)在这30名被调查者中,药物浓度m不低于7的有__________人;
(2)将15名服用药物的甲流患者的病毒载量n的方差记作s,15名服用药物的乙流患者的病毒载量n的方差记作s,则s__________s;(填“>”“<”或“=”)
(3)将“药物浓度1≤m≤7,病毒载量1≤n≤2”作为该药物“有效”的依据,药物正式投入市场后,请你估计服用该药物的600名甲流患者中“有效”的人数.
图6
第二十章 数据的分析
1.B 2.B 3.24 4.100
5.解:(1)甲这三个方面的平均得分为 =(分).
乙这三个方面的平均得分为 =(分).
∵>,∴该公司会录用甲.
(2)“学历”所占比例为 =.
“能力”所占比例为 =.
“经验”所占比例为 =.
∴“学历”“能力”“经验”的比为2∶3∶1.
甲的综合成绩为 =7(分).
乙的综合成绩为 =8(分).
∵8>7,∴该公司会录用乙.∴会改变(1)的录用结果.
6.解:(1)6 3 77.5.(2)小明.
(3)700×50%=350(名).
答:估计九年级有350名学生的竞赛成绩达到优秀.
7.5 12
8.解:(1)7 7 7.5 3.
(2)s=×[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2]=1.2.
s=×[(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
(3)①从平均数来看,甲、乙两人成绩的平均数相同,说明两人的平均水平相同;而甲的方差小于乙的方差,说明甲的成绩更稳定.
②从平均数来看,甲、乙两人成绩的平均数相同,说明两人的平均水平相同;而乙命中9环及9环以上的次数大于甲,所以乙的成绩更好些.
③从图5中两人射击命中环数的走势看乙更有潜力.
9.解:(1)4.
(2)<.
(3)通过统计图可以得到“药物浓度1≤m≤7,病毒载量1≤n≤2”的甲流患者人数为7.
∴600×=280.
答:估计服用该药物的600名甲流患者中“有效”的人数为280.
考点1 平均数、中位数、众数
1.某中学积极推进学生综合素质评价改革,该中学学生小明本学期德、智、体、美、劳五项的评价得分如图1所示,则小明同学五项评价得分的众数、中位数、平均数分别为( )
A.9,9,8.4 B.9,9,8.6 C.8,8,8.6 D.9,8,8.4
图1 图2
2.某校篮球社团共有30名球员,该社团成员的年龄情况如下表.对于不同的x,下列关于这30名球员年龄的统计量不会发生改变的是( )
年龄(岁) 13 14 15 16
人数(名) 8 12 x 10-x
A.平均数、中位数 B.众数,中位数 C.众数、方差 D.平均数、方差
3.商家准备将2千克甲种糖果和3千克乙种糖果混合成一袋什锦糖果,甲种糖果的价格为30元/千克,乙种糖果的价格为20元/千克.若要保证利润不变,则这袋什锦糖果的价格应为__________元/千克.
4.小敏同学本学期数学前三次考试的成绩(满分120分)分别是:阶段一90分;期中100分;阶段三95分.若按照如图2所示的权重来计算本学期数学的总评成绩,小敏同学要想本学期数学的总评成绩不低于98分,则期末数学至少要考__________分.
5.某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三个方面进行了评分,评分(满分10分)结果如图3所示.成绩高者被录用.
(1)分别求出甲、乙两人这三个方面的平均得分,并指出该公司会录用谁;
(2)请将这三个方面的得分按照扇形统计图(图4)所示占比,分别计算甲、乙两人的综合成绩,并说明是否会改变(1)的录用结果.
6.为了进一步推进学校安全教育,切实增强广大学生的安全防范意识和自护自救能力,某校举行了安全知识网络竞赛活动,满分为100分.为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级抽取了20名参赛学生的成绩.已知抽到的八年级的竞赛成绩(单位:分)如下:80,95,60,80,75,60,95,65,75,70,80,75,85,65,90,70,75,80,85,80.注:分数在80分以上(不含80分)为优秀.
为了便于分析数据,统计员对八年级的数据进行了整理,得到下表:
成绩等级 成绩(分) 学生数
D级 60≤x≤70 a
C级 70<x≤80 9
B级 80<x≤90 b
A级 90<x≤100 2
八、九年级所抽取学生的竞赛成绩的平均数、中位数、优秀率如下表:
年级 平均数 中位数 优秀率
八年级 77 c 25%
九年级 78.5 82.5 50%
(1)填空:a=__________,b=__________,c=__________;
(2)八年级学生小明和九年级学生小亮的此次竞赛成绩都是80分,则这两名同学在各自年级的排名__________更靠前;(填“小明”或“小亮”)
(3)若该校九年级共有700名学生参加此次竞赛,请估计九年级有多少名学生的竞赛成绩达到优秀.
考点2 方差
7.已知一组数据x1,x2,x3,x4,x5的平均数是4,方差是3,另一组数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的平均数是__________,方差是__________.
8.甲、乙两人在相同条件下各射击10次,每次射击的成绩情况如图5所示.
图5
根据图示信息,整理分析数据如下表:
平均数 中位数 众数 命中9环及9环以上的次数
甲 7 7 a 1
乙 b c 7,8,9 d
(1)填空:a=________,b=________,c=________,d=________.
(2)计算甲、乙两人这10次射击成绩的方差.
(3)请从下列不同的角度对甲、乙两人这10次射击的成绩进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩更好些);
③从图5中两人射击命中环数的走势看(分析谁更有潜力).
9.药物研发机构为对比研究某种药物对甲、乙两种流感(简称甲流、乙流)的疗效,需要检测患者体内的药物浓度m和病毒载量n两个指标,该机构分别在服用该药物的甲流患者和乙流患者中,各随机选取15人作为调查对象,将收集到的数据整理后,绘制成如图6所示的统计图.
根据以上信息,回答下列问题:
(1)在这30名被调查者中,药物浓度m不低于7的有__________人;
(2)将15名服用药物的甲流患者的病毒载量n的方差记作s,15名服用药物的乙流患者的病毒载量n的方差记作s,则s__________s;(填“>”“<”或“=”)
(3)将“药物浓度1≤m≤7,病毒载量1≤n≤2”作为该药物“有效”的依据,药物正式投入市场后,请你估计服用该药物的600名甲流患者中“有效”的人数.
图6
第二十章 数据的分析
1.B 2.B 3.24 4.100
5.解:(1)甲这三个方面的平均得分为 =(分).
乙这三个方面的平均得分为 =(分).
∵>,∴该公司会录用甲.
(2)“学历”所占比例为 =.
“能力”所占比例为 =.
“经验”所占比例为 =.
∴“学历”“能力”“经验”的比为2∶3∶1.
甲的综合成绩为 =7(分).
乙的综合成绩为 =8(分).
∵8>7,∴该公司会录用乙.∴会改变(1)的录用结果.
6.解:(1)6 3 77.5.(2)小明.
(3)700×50%=350(名).
答:估计九年级有350名学生的竞赛成绩达到优秀.
7.5 12
8.解:(1)7 7 7.5 3.
(2)s=×[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2]=1.2.
s=×[(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
(3)①从平均数来看,甲、乙两人成绩的平均数相同,说明两人的平均水平相同;而甲的方差小于乙的方差,说明甲的成绩更稳定.
②从平均数来看,甲、乙两人成绩的平均数相同,说明两人的平均水平相同;而乙命中9环及9环以上的次数大于甲,所以乙的成绩更好些.
③从图5中两人射击命中环数的走势看乙更有潜力.
9.解:(1)4.
(2)<.
(3)通过统计图可以得到“药物浓度1≤m≤7,病毒载量1≤n≤2”的甲流患者人数为7.
∴600×=280.
答:估计服用该药物的600名甲流患者中“有效”的人数为280.
