第十八章平行四边形 知识点分类练(含答案) 2024-2025学年数学人教版八年级下册
文档属性
| 名称 | 第十八章平行四边形 知识点分类练(含答案) 2024-2025学年数学人教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形
考点1 平行四边形的性质与判定
1.如图1,在 ABCD中,以点B为圆心,适当长为半径作弧,分别交AB,BC于点F,G,分别以点F,G为圆心,大于 FG的长为半径作弧,两弧交于点H,连接BH并延长,交AD于点E,连接CE.若AB=10,DE=6,CE=8,则BE的长为__________.
图1 图2 图3
2.在平面直角坐标系中,点A,B,C的坐标分别为(0,0),(4,0),(3,2),以A,B,C三点为顶点画平行四边形,则第四个顶点不可能在第__________象限.
3.如图2,在△ABC中,∠BAC=45°,AB=AC=2,P为边AB上一动点,以PA,PC为边作 PAQC,则对角线PQ的最小值为__________.
4.如图3,在 ABCD中,E是CD的中点,过点B作BF⊥AD于点F,连接EF.若AB=5,BC=4,DF=1,则BE的长为__________.
5.如图4,在△ABC中,点D在边AB上,E是AC的中点,连接DE并延长到点F,使得CF∥AB,连接AF,CF,CD.
(1)求证:四边形AFCD是平行四边形;
(2)若△ADC为等边三角形,AD=6,求DF的长.
图4
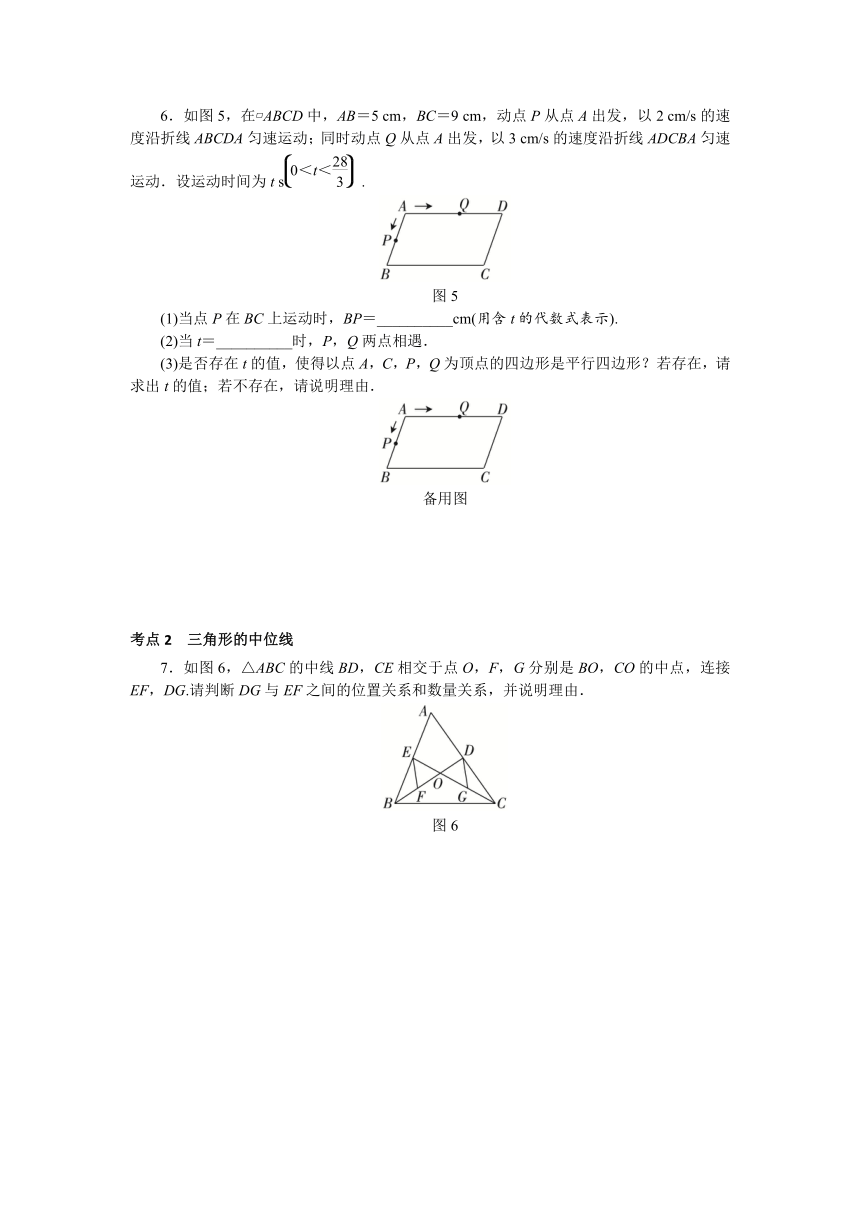
6.如图5,在 ABCD中,AB=5 cm,BC=9 cm,动点P从点A出发,以2 cm/s的速度沿折线ABCDA匀速运动;同时动点Q从点A出发,以3 cm/s的速度沿折线ADCBA匀速运动.设运动时间为t s.
图5
(1)当点P在BC上运动时,BP=__________cm(用含t的代数式表示).
(2)当t=__________时,P,Q两点相遇.
(3)是否存在t的值,使得以点A,C,P,Q为顶点的四边形是平行四边形?若存在,请求出t的值;若不存在,请说明理由.
备用图
考点2 三角形的中位线
7.如图6,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点,连接EF,DG.请判断DG与EF之间的位置关系和数量关系,并说明理由.
图6
8.如图7,在四边形ABCD中,∠A=90°,AB=3,AD=,M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则线段EF的最大值为__________.
图7 图8
9.如图8,AD为△ABC外角的平分线,BD⊥AD于点D,E为BC的中点,DE=4,AC=2,则AB的长为__________.
考点3 矩形的性质与判定
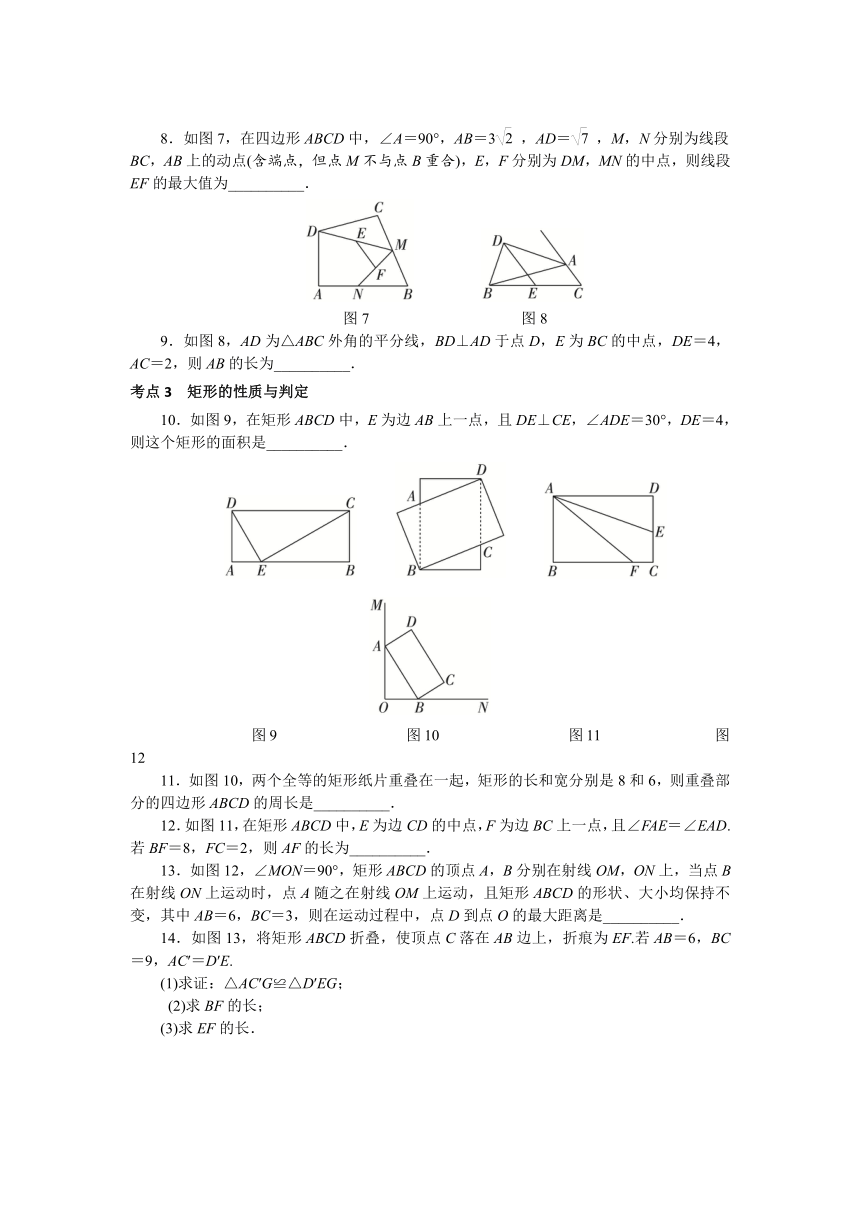
10.如图9,在矩形ABCD中,E为边AB上一点,且DE⊥CE,∠ADE=30°,DE=4,则这个矩形的面积是__________.
图9 图10 图11 图12
11.如图10,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是8和6,则重叠部分的四边形ABCD的周长是__________.
12.如图11,在矩形ABCD中,E为边CD的中点,F为边BC上一点,且∠FAE=∠EAD.若BF=8,FC=2,则AF的长为__________.
13.如图12,∠MON=90°,矩形ABCD的顶点A,B分别在射线OM,ON上,当点B在射线ON上运动时,点A随之在射线OM上运动,且矩形ABCD的形状、大小均保持不变,其中AB=6,BC=3,则在运动过程中,点D到点O的最大距离是__________.
14.如图13,将矩形ABCD折叠,使顶点C落在AB边上,折痕为EF.若AB=6,BC=9,AC′=D′E.
(1)求证:△AC′G≌△D′EG;
(2)求BF的长;
(3)求EF的长.
图13
15.综合与实践
(1)推理证明:如图14①,在Rt△ABC中,∠ACB=90°,若CD是斜边AB上的中线,则CD=AB.请你用矩形的性质证明这个结论的正确性.
(2)迁移运用:利用上述结论解决下列问题:
①如图14②,在线段BD的两侧以BD为斜边分别构造Rt△ABD与Rt△CBD,其中∠BAD=∠BCD=90°,E,F分别是BD,AC的中点.请判断EF与AC的位置关系,并说明理由.
②如图14③,在 ABCD中,对角线AC,BD相交于点O,分别以AC,BD为斜边且在同侧构造Rt△ACE与Rt△BDE,其中∠AEC=∠BED=90°.求证:四边形ABCD是矩形.
图14
考点4 菱形的性质与判定
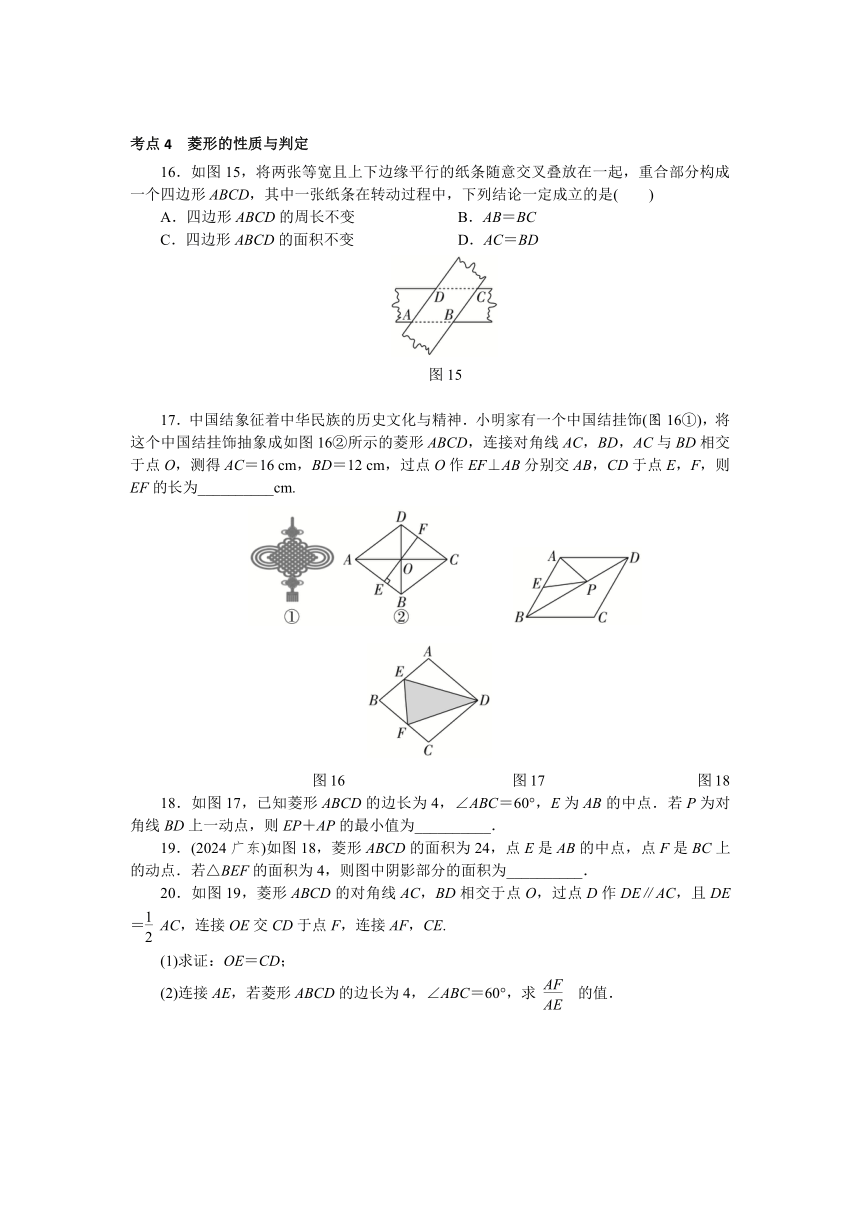
16.如图15,将两张等宽且上下边缘平行的纸条随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD的周长不变 B.AB=BC
C.四边形ABCD的面积不变 D.AC=BD
图15
17.中国结象征着中华民族的历史文化与精神.小明家有一个中国结挂饰(图16①),将这个中国结挂饰抽象成如图16②所示的菱形ABCD,连接对角线AC,BD,AC与BD相交于点O,测得AC=16 cm,BD=12 cm,过点O作EF⊥AB分别交AB,CD于点E,F,则EF的长为__________cm.
图16 图17 图18
18.如图17,已知菱形ABCD的边长为4,∠ABC=60°,E为AB的中点.若P为对角线BD上一动点,则EP+AP的最小值为__________.
19.(2024广东)如图18,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则图中阴影部分的面积为__________.
20.如图19,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC,且DE=AC,连接OE交CD于点F,连接AF,CE.
(1)求证:OE=CD;
(2)连接AE,若菱形ABCD的边长为4,∠ABC=60°,求 的值.
图19
考点5 正方形的性质与判定
21.如图20,在平面直角坐标系中,正方形ABCD的边AB在x轴上,A(-2,0),B(3,0).现固定点A,B在x轴上的位置不变,把正方形沿箭头方向推,使点D落在y轴正半轴上的点D′处,则点C的对应点C′的坐标为__________.
图20 图21 图22 图23
22.如图21,在正方形ABCD内有两点E,F,若AB=5,AE=FC=4,BF=DE=3,则EF的长为__________.
23.如图22,点A,B,E在同一条直线上,正方形ABCD、正方形BEFG的边长分别为6,8,H为线段DF的中点,连接BH,则BH的长为__________.
24.如图23,在正方形ABCD中,E为边AB上一点,过点D作DF⊥DE,交BC的延长线于点F,连接EF,与边CD交于点G,与对角线BD交于点H,DI⊥EF交BC于点I.下列结论:①AE=CF;②EF=DF;③∠ADE+∠EFB=45°;④若BF=BD=,则BE=2-;⑤连接EI,则EI=AE+CI.其中正确的是__________.(填序号)
25.如图24①,正方形ABCD的边长为4,点M,N分别在边AB,BC上,且BM=CN=1,连接CM,DN,CM与DN相交于点O.
(1)探究线段CM与DN之间的数量关系和位置关系,并说明理由;
(2)如图24②,若E,F分别是DN与CM的中点,求EF的长;
(3)如图24③,延长CM至点P,连接BP,使∠BPC=45°,请直接写出线段PM的长.
图24
第十八章 平行四边形
1.8 2.三 3.
4. 【提示】如答图1,延长FE交BC的延长线于点G.易得△DEF≌△CEG,△BFG是直角三角形.
答图1
5.(1)证明:∵E是AC的中点,
∴CE=AE.
∵CF∥AB,∴∠CFE=∠ADE.
在△CFE和△ADE中,
∴△CFE≌△ADE(AAS).∴DE=FE.
又CE=AE,∴四边形AFCD是平行四边形.
(2)解:∵△ADC为等边三角形,∴AD=AC=6.
由(1)知,CE=AE.∴CE=AE=AC=3,且DE⊥AC.
在Rt△ADE中,由勾股定理,
得DE===3.
∵四边形AFCD是平行四边形,
∴DF=2DE=6.∴DF的长是6.
6.解:(1)(2t-5).(2).
(3)存在.
①如答图2,当四边形APCQ为平行四边形时,PC=AQ.
答图2
由题意,得PC=(14-2t)cm,AQ=3t cm.
∴14-2t=3t.解得t=.
②如答图3,当四边形AQCP为平行四边形时,AQ=PC.
答图3
由题意,得AQ=(28-3t)cm,PC=(2t-14)cm.
∴28-3t=2t-14.解得t=.综上,t的值为 或 .
7.解:DG∥EF,且DG=EF.理由如下:如答图4,连接AO.
答图4
∵CE是△ABC的中线,∴E是AB的中点.
又F是BO的中点,∴EF是△ABO的中位线.∴EF∥AO,EF=AO.
同理,得DG∥AO,DG=AO.∴DG∥EF,且DG=EF.
8.2.5
9.6 【提示】如答图5,延长BD,CA交于点H.易得△ABH是等腰三角形,D是BH的中点,DE是△BCH的中位线.
答图5
10.16 11.25
12.12 【提示】如答图6,延长BC,AE交于点H.易得△ADE≌△HCE,△AFH为等腰三角形.
答图6
13.3+3 【提示】如答图7,取AB的中点E,连接OD,OE,DE.易得OE,DE的长为定值,根据三角形的三边关系,得OD≤OE+DE.
答图7
14.(1)证明:∵四边形ABCD是矩形,
∴CD=AB=6,∠A=∠D=90°.
由折叠的性质,得∠D′=∠D=90°.
∴∠A=∠D′.
在△AC′G和△D′EG中,
∴△AC′G≌△D′EG(AAS).
(2)解:由(1),得△AC′G≌△D′EG.
∴AG=D′G,C′G=EG.
由折叠的性质,得D′E=DE,C′D′=CD,C′F=CF.
∴AE=AG+GE=D′G+C′G=C′D′=CD=6.
∵四边形ABCD是矩形,∴AD=BC=9.
∴AC′=D′E=DE=AD-AE=3.∴BC′=AB-AC′=3.
在Rt△BC′F中,由勾股定理,得C′F2=BF2+BC′2,
即CF2=(9-CF)2+32.
∴CF=5.∴BF=9-CF=4.
(3)解:如答图8,过点E作EH⊥BC于点H,则四边形CDEH是矩形.
答图8
∴CH=DE=3,EH=CD=6.
∴FH=CF-CH=5-3=2.
在Rt△EFH中,由勾股定理,得
EF===2.
15.(1)证明:如答图9,延长CD到点E,使DE=CD,连接AE,BE.
答图9
∵CD是斜边AB上的中线,∴AD=BD.
又CD=DE,
∴四边形ACBE是平行四边形.
又∠ACB=90°,
∴平行四边形ACBE是矩形.
∴AB=CE.∴CD=CE=AB.
(2)①解:EF⊥AC.理由如下:
如答图10,连接AE,CE.
答图10
在Rt△ABD中,∠BAD=90°,E为斜边BD的中点,
∴AE=BD.
在Rt△CBD中,∠BCD=90°,E为斜边BD的中点,
∴CE=BD.∴AE=CE.又F是AC的中点,∴EF⊥AC.
②证明:如答图11,连接EO.
答图11
∵四边形ABCD是平行四边形,∴O为AC,BD的中点.
在Rt△ACE中,∠AEC=90°,O为斜边AC的中点,
∴EO=AC.
在Rt△BDE中,∠BED=90°,O为斜边BD的中点,
∴EO=BD.∴AC=BD.∴四边形ABCD是矩形.
16.B 17. 18.2
19.10 【提示】如答图12,连接BD,CE.根据菱形的性质,易得S△BEC=S△AED=6.根据S△BEF=4,可得FC=BC.
答图12
20.(1)证明:四边形ABCD是菱形,
∴OA=OC=AC,AD=CD.
∵DE∥AC,DE=AC,∴DE=OA=OC.
∴四边形OADE、四边形OCED都是平行四边形.
∴OE=AD.∴OE=CD.
(2)解:如答图13,连接AE.
答图13
由(1)可知,四边形OCED是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.∴∠COD=90°.
∴四边形OCED是矩形.
∴CF=DF.
在菱形ABCD中,∠ABC=60°,
∴AC=AB=CD=AD=4,CF=CD=2,AO=AC=2.
∴AF⊥CD.
在Rt△ACF中,由勾股定理,得AF===2.
在Rt△AOD中,由勾股定理,得OD===2.
在矩形OCED中,CE=OD=2.
在Rt△ACE中,AE===2.
∴==.
21.(5,) 22.
23.5 【提示】如答图14,连接BD,BF.根据正方形的性质,得△BDF是直角三角形.
答图14
24.①②③④⑤
25.解:(1)CM=DN,且CM⊥DN.理由如下:
∵四边形ABCD是正方形,
∴BC=CD,∠B=∠NCD=90°.
在△BCM和△CDN中,
∴△BCM≌△CDN(SAS).∴CM=DN,∠BCM=∠CDN.
∵∠BCM+∠MCD=∠BCD=90°,∴∠CDN+∠MCD=90°.
∴∠COD=90°,即CM⊥DN.
(2)如答图15,连接CE并延长交AD于点G,连接GM.
答图15
∵四边形ABCD是正方形,
∴∠A=90°,BC∥AD.
∴∠ENC=∠EDG.
∵E是DN的中点,∴NE=DE.
在△CNE和△GDE中,
∴△CNE≌△GDE(ASA).∴CE=GE,GD=CN=1.
又F是CM的中点,∴EF为△CGM的中位线.
∴EF=MG.
∵正方形ABCD的边长为4,∴AB=AD=4.
∴AG=AD-GD=3,AM=AB-BM=3.
在Rt△AGM中,由勾股定理,
得MG===3.
∴EF=MG=.
(3)PM=.
【提示】如答图16,过点B作BH⊥CM于点H.
答图16
在Rt△CBM中,由勾股定理,得CM===.
∵S△BCM=CM·BH=BC·BM,
∴BH==.
在Rt△BCH中,由勾股定理,得CH==.
∵∠BPC=45°,∠BHP=90°,
∴△BHP是等腰直角三角形,PH=BH=.
∴PC=PH+CH=.∴PM=PC-CM=.
考点1 平行四边形的性质与判定
1.如图1,在 ABCD中,以点B为圆心,适当长为半径作弧,分别交AB,BC于点F,G,分别以点F,G为圆心,大于 FG的长为半径作弧,两弧交于点H,连接BH并延长,交AD于点E,连接CE.若AB=10,DE=6,CE=8,则BE的长为__________.
图1 图2 图3
2.在平面直角坐标系中,点A,B,C的坐标分别为(0,0),(4,0),(3,2),以A,B,C三点为顶点画平行四边形,则第四个顶点不可能在第__________象限.
3.如图2,在△ABC中,∠BAC=45°,AB=AC=2,P为边AB上一动点,以PA,PC为边作 PAQC,则对角线PQ的最小值为__________.
4.如图3,在 ABCD中,E是CD的中点,过点B作BF⊥AD于点F,连接EF.若AB=5,BC=4,DF=1,则BE的长为__________.
5.如图4,在△ABC中,点D在边AB上,E是AC的中点,连接DE并延长到点F,使得CF∥AB,连接AF,CF,CD.
(1)求证:四边形AFCD是平行四边形;
(2)若△ADC为等边三角形,AD=6,求DF的长.
图4
6.如图5,在 ABCD中,AB=5 cm,BC=9 cm,动点P从点A出发,以2 cm/s的速度沿折线ABCDA匀速运动;同时动点Q从点A出发,以3 cm/s的速度沿折线ADCBA匀速运动.设运动时间为t s.
图5
(1)当点P在BC上运动时,BP=__________cm(用含t的代数式表示).
(2)当t=__________时,P,Q两点相遇.
(3)是否存在t的值,使得以点A,C,P,Q为顶点的四边形是平行四边形?若存在,请求出t的值;若不存在,请说明理由.
备用图
考点2 三角形的中位线
7.如图6,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点,连接EF,DG.请判断DG与EF之间的位置关系和数量关系,并说明理由.
图6
8.如图7,在四边形ABCD中,∠A=90°,AB=3,AD=,M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则线段EF的最大值为__________.
图7 图8
9.如图8,AD为△ABC外角的平分线,BD⊥AD于点D,E为BC的中点,DE=4,AC=2,则AB的长为__________.
考点3 矩形的性质与判定
10.如图9,在矩形ABCD中,E为边AB上一点,且DE⊥CE,∠ADE=30°,DE=4,则这个矩形的面积是__________.
图9 图10 图11 图12
11.如图10,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是8和6,则重叠部分的四边形ABCD的周长是__________.
12.如图11,在矩形ABCD中,E为边CD的中点,F为边BC上一点,且∠FAE=∠EAD.若BF=8,FC=2,则AF的长为__________.
13.如图12,∠MON=90°,矩形ABCD的顶点A,B分别在射线OM,ON上,当点B在射线ON上运动时,点A随之在射线OM上运动,且矩形ABCD的形状、大小均保持不变,其中AB=6,BC=3,则在运动过程中,点D到点O的最大距离是__________.
14.如图13,将矩形ABCD折叠,使顶点C落在AB边上,折痕为EF.若AB=6,BC=9,AC′=D′E.
(1)求证:△AC′G≌△D′EG;
(2)求BF的长;
(3)求EF的长.
图13
15.综合与实践
(1)推理证明:如图14①,在Rt△ABC中,∠ACB=90°,若CD是斜边AB上的中线,则CD=AB.请你用矩形的性质证明这个结论的正确性.
(2)迁移运用:利用上述结论解决下列问题:
①如图14②,在线段BD的两侧以BD为斜边分别构造Rt△ABD与Rt△CBD,其中∠BAD=∠BCD=90°,E,F分别是BD,AC的中点.请判断EF与AC的位置关系,并说明理由.
②如图14③,在 ABCD中,对角线AC,BD相交于点O,分别以AC,BD为斜边且在同侧构造Rt△ACE与Rt△BDE,其中∠AEC=∠BED=90°.求证:四边形ABCD是矩形.
图14
考点4 菱形的性质与判定
16.如图15,将两张等宽且上下边缘平行的纸条随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD的周长不变 B.AB=BC
C.四边形ABCD的面积不变 D.AC=BD
图15
17.中国结象征着中华民族的历史文化与精神.小明家有一个中国结挂饰(图16①),将这个中国结挂饰抽象成如图16②所示的菱形ABCD,连接对角线AC,BD,AC与BD相交于点O,测得AC=16 cm,BD=12 cm,过点O作EF⊥AB分别交AB,CD于点E,F,则EF的长为__________cm.
图16 图17 图18
18.如图17,已知菱形ABCD的边长为4,∠ABC=60°,E为AB的中点.若P为对角线BD上一动点,则EP+AP的最小值为__________.
19.(2024广东)如图18,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则图中阴影部分的面积为__________.
20.如图19,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC,且DE=AC,连接OE交CD于点F,连接AF,CE.
(1)求证:OE=CD;
(2)连接AE,若菱形ABCD的边长为4,∠ABC=60°,求 的值.
图19
考点5 正方形的性质与判定
21.如图20,在平面直角坐标系中,正方形ABCD的边AB在x轴上,A(-2,0),B(3,0).现固定点A,B在x轴上的位置不变,把正方形沿箭头方向推,使点D落在y轴正半轴上的点D′处,则点C的对应点C′的坐标为__________.
图20 图21 图22 图23
22.如图21,在正方形ABCD内有两点E,F,若AB=5,AE=FC=4,BF=DE=3,则EF的长为__________.
23.如图22,点A,B,E在同一条直线上,正方形ABCD、正方形BEFG的边长分别为6,8,H为线段DF的中点,连接BH,则BH的长为__________.
24.如图23,在正方形ABCD中,E为边AB上一点,过点D作DF⊥DE,交BC的延长线于点F,连接EF,与边CD交于点G,与对角线BD交于点H,DI⊥EF交BC于点I.下列结论:①AE=CF;②EF=DF;③∠ADE+∠EFB=45°;④若BF=BD=,则BE=2-;⑤连接EI,则EI=AE+CI.其中正确的是__________.(填序号)
25.如图24①,正方形ABCD的边长为4,点M,N分别在边AB,BC上,且BM=CN=1,连接CM,DN,CM与DN相交于点O.
(1)探究线段CM与DN之间的数量关系和位置关系,并说明理由;
(2)如图24②,若E,F分别是DN与CM的中点,求EF的长;
(3)如图24③,延长CM至点P,连接BP,使∠BPC=45°,请直接写出线段PM的长.
图24
第十八章 平行四边形
1.8 2.三 3.
4. 【提示】如答图1,延长FE交BC的延长线于点G.易得△DEF≌△CEG,△BFG是直角三角形.
答图1
5.(1)证明:∵E是AC的中点,
∴CE=AE.
∵CF∥AB,∴∠CFE=∠ADE.
在△CFE和△ADE中,
∴△CFE≌△ADE(AAS).∴DE=FE.
又CE=AE,∴四边形AFCD是平行四边形.
(2)解:∵△ADC为等边三角形,∴AD=AC=6.
由(1)知,CE=AE.∴CE=AE=AC=3,且DE⊥AC.
在Rt△ADE中,由勾股定理,
得DE===3.
∵四边形AFCD是平行四边形,
∴DF=2DE=6.∴DF的长是6.
6.解:(1)(2t-5).(2).
(3)存在.
①如答图2,当四边形APCQ为平行四边形时,PC=AQ.
答图2
由题意,得PC=(14-2t)cm,AQ=3t cm.
∴14-2t=3t.解得t=.
②如答图3,当四边形AQCP为平行四边形时,AQ=PC.
答图3
由题意,得AQ=(28-3t)cm,PC=(2t-14)cm.
∴28-3t=2t-14.解得t=.综上,t的值为 或 .
7.解:DG∥EF,且DG=EF.理由如下:如答图4,连接AO.
答图4
∵CE是△ABC的中线,∴E是AB的中点.
又F是BO的中点,∴EF是△ABO的中位线.∴EF∥AO,EF=AO.
同理,得DG∥AO,DG=AO.∴DG∥EF,且DG=EF.
8.2.5
9.6 【提示】如答图5,延长BD,CA交于点H.易得△ABH是等腰三角形,D是BH的中点,DE是△BCH的中位线.
答图5
10.16 11.25
12.12 【提示】如答图6,延长BC,AE交于点H.易得△ADE≌△HCE,△AFH为等腰三角形.
答图6
13.3+3 【提示】如答图7,取AB的中点E,连接OD,OE,DE.易得OE,DE的长为定值,根据三角形的三边关系,得OD≤OE+DE.
答图7
14.(1)证明:∵四边形ABCD是矩形,
∴CD=AB=6,∠A=∠D=90°.
由折叠的性质,得∠D′=∠D=90°.
∴∠A=∠D′.
在△AC′G和△D′EG中,
∴△AC′G≌△D′EG(AAS).
(2)解:由(1),得△AC′G≌△D′EG.
∴AG=D′G,C′G=EG.
由折叠的性质,得D′E=DE,C′D′=CD,C′F=CF.
∴AE=AG+GE=D′G+C′G=C′D′=CD=6.
∵四边形ABCD是矩形,∴AD=BC=9.
∴AC′=D′E=DE=AD-AE=3.∴BC′=AB-AC′=3.
在Rt△BC′F中,由勾股定理,得C′F2=BF2+BC′2,
即CF2=(9-CF)2+32.
∴CF=5.∴BF=9-CF=4.
(3)解:如答图8,过点E作EH⊥BC于点H,则四边形CDEH是矩形.
答图8
∴CH=DE=3,EH=CD=6.
∴FH=CF-CH=5-3=2.
在Rt△EFH中,由勾股定理,得
EF===2.
15.(1)证明:如答图9,延长CD到点E,使DE=CD,连接AE,BE.
答图9
∵CD是斜边AB上的中线,∴AD=BD.
又CD=DE,
∴四边形ACBE是平行四边形.
又∠ACB=90°,
∴平行四边形ACBE是矩形.
∴AB=CE.∴CD=CE=AB.
(2)①解:EF⊥AC.理由如下:
如答图10,连接AE,CE.
答图10
在Rt△ABD中,∠BAD=90°,E为斜边BD的中点,
∴AE=BD.
在Rt△CBD中,∠BCD=90°,E为斜边BD的中点,
∴CE=BD.∴AE=CE.又F是AC的中点,∴EF⊥AC.
②证明:如答图11,连接EO.
答图11
∵四边形ABCD是平行四边形,∴O为AC,BD的中点.
在Rt△ACE中,∠AEC=90°,O为斜边AC的中点,
∴EO=AC.
在Rt△BDE中,∠BED=90°,O为斜边BD的中点,
∴EO=BD.∴AC=BD.∴四边形ABCD是矩形.
16.B 17. 18.2
19.10 【提示】如答图12,连接BD,CE.根据菱形的性质,易得S△BEC=S△AED=6.根据S△BEF=4,可得FC=BC.
答图12
20.(1)证明:四边形ABCD是菱形,
∴OA=OC=AC,AD=CD.
∵DE∥AC,DE=AC,∴DE=OA=OC.
∴四边形OADE、四边形OCED都是平行四边形.
∴OE=AD.∴OE=CD.
(2)解:如答图13,连接AE.
答图13
由(1)可知,四边形OCED是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.∴∠COD=90°.
∴四边形OCED是矩形.
∴CF=DF.
在菱形ABCD中,∠ABC=60°,
∴AC=AB=CD=AD=4,CF=CD=2,AO=AC=2.
∴AF⊥CD.
在Rt△ACF中,由勾股定理,得AF===2.
在Rt△AOD中,由勾股定理,得OD===2.
在矩形OCED中,CE=OD=2.
在Rt△ACE中,AE===2.
∴==.
21.(5,) 22.
23.5 【提示】如答图14,连接BD,BF.根据正方形的性质,得△BDF是直角三角形.
答图14
24.①②③④⑤
25.解:(1)CM=DN,且CM⊥DN.理由如下:
∵四边形ABCD是正方形,
∴BC=CD,∠B=∠NCD=90°.
在△BCM和△CDN中,
∴△BCM≌△CDN(SAS).∴CM=DN,∠BCM=∠CDN.
∵∠BCM+∠MCD=∠BCD=90°,∴∠CDN+∠MCD=90°.
∴∠COD=90°,即CM⊥DN.
(2)如答图15,连接CE并延长交AD于点G,连接GM.
答图15
∵四边形ABCD是正方形,
∴∠A=90°,BC∥AD.
∴∠ENC=∠EDG.
∵E是DN的中点,∴NE=DE.
在△CNE和△GDE中,
∴△CNE≌△GDE(ASA).∴CE=GE,GD=CN=1.
又F是CM的中点,∴EF为△CGM的中位线.
∴EF=MG.
∵正方形ABCD的边长为4,∴AB=AD=4.
∴AG=AD-GD=3,AM=AB-BM=3.
在Rt△AGM中,由勾股定理,
得MG===3.
∴EF=MG=.
(3)PM=.
【提示】如答图16,过点B作BH⊥CM于点H.
答图16
在Rt△CBM中,由勾股定理,得CM===.
∵S△BCM=CM·BH=BC·BM,
∴BH==.
在Rt△BCH中,由勾股定理,得CH==.
∵∠BPC=45°,∠BHP=90°,
∴△BHP是等腰直角三角形,PH=BH=.
∴PC=PH+CH=.∴PM=PC-CM=.
