第十九章一次函数 限时检测卷 (含答案)2024-2025学年数学人教版八年级下册
文档属性
| 名称 | 第十九章一次函数 限时检测卷 (含答案)2024-2025学年数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 147.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 16:21:13 | ||
图片预览



文档简介
第十九章一次函数 限时检测卷
时间:100分钟 分值:120分 得分:__________
一、选择题(本大题共10小题,每小题3分,共30分)
1.在利用太阳能热水器加热水的过程中,热水器里的水温随所晒时间的长短而变化,在这个问题中,自变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
2.函数y=的自变量x的取值范围是( )
A.x≥2 B.x≤2 C.x≥-2 D.x≤-2
3.一次函数y=-2x+6的图象与x轴的交点坐标是( )
A.(0,3) B.(3,0) C.(0,6) D.(6,0)
4.把直线y=-x-5向下平移3个单位长度得到直线l,则直线l对应的解析式是( )
A.y=-x-2 B.y=-x-8 C.y=3x-5 D.y=-3x-8
5.若函数y=(m-1)x|m|-5是关于x的一次函数,则m的值为( )
A.±1 B.1 C.-1 D.2
6.一次函数y=kx+b的图象如图1所示,则k,b的取值范围是( )
图1
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
7.已知点(-1,y1),(2,y2)在直线y=-x+b上,则y1,y2的大小关系是( )
A.y1>y2 B.y18.如图2,直线y=-x+3与y=mx+n的交点的横坐标为1,则关于x,y的二元一次方程组的解为( )
图2
A. B. C. D.
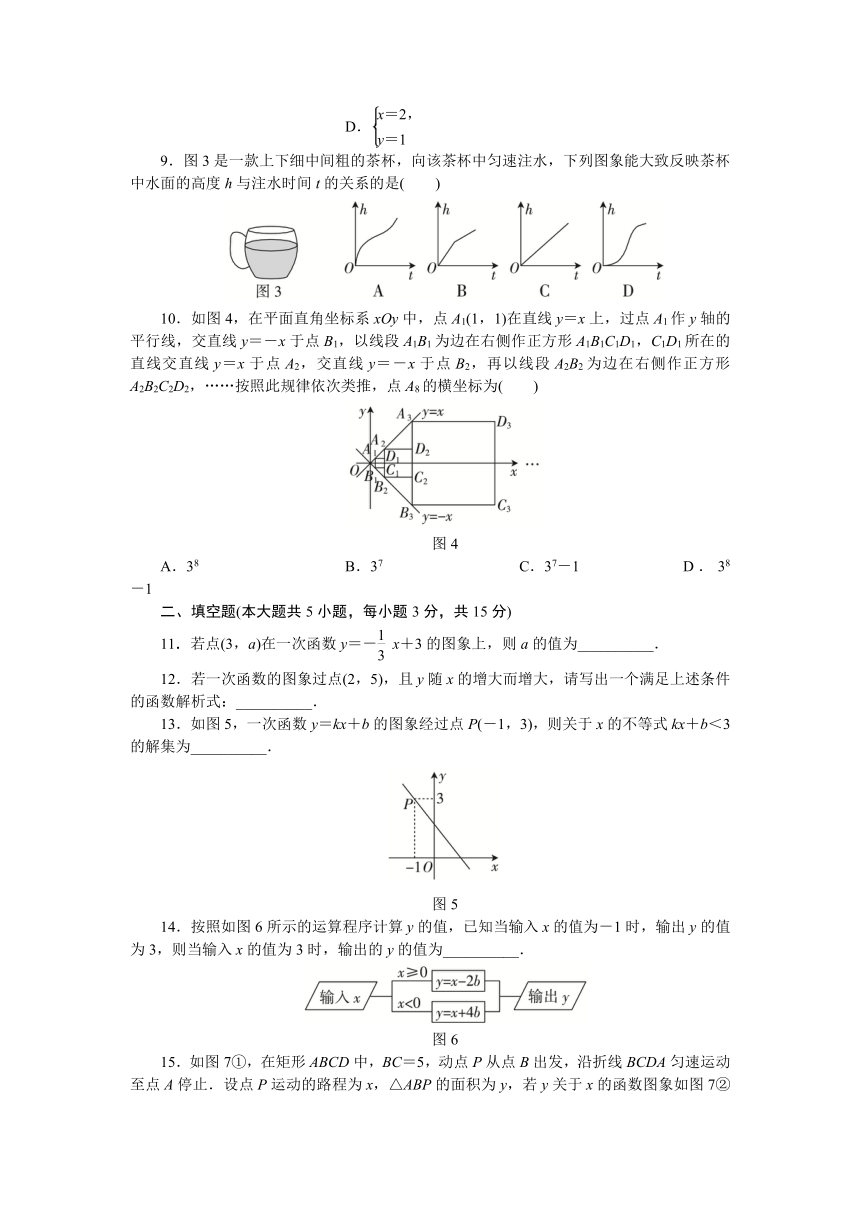
9.图3是一款上下细中间粗的茶杯,向该茶杯中匀速注水,下列图象能大致反映茶杯中水面的高度h与注水时间t的关系的是( )
10.如图4,在平面直角坐标系xOy中,点A1(1,1)在直线y=x上,过点A1作y轴的平行线,交直线y=-x于点B1,以线段A1B1为边在右侧作正方形A1B1C1D1,C1D1所在的直线交直线y=x于点A2,交直线y=-x于点B2,再以线段A2B2为边在右侧作正方形A2B2C2D2,……按照此规律依次类推,点A8的横坐标为( )
图4
A.38 B.37 C.37-1 D.38-1
二、填空题(本大题共5小题,每小题3分,共15分)
11.若点(3,a)在一次函数y=-x+3的图象上,则a的值为__________.
12.若一次函数的图象过点(2,5),且y随x的增大而增大,请写出一个满足上述条件的函数解析式:__________.
13.如图5,一次函数y=kx+b的图象经过点P(-1,3),则关于x的不等式kx+b<3的解集为__________.
图5
14.按照如图6所示的运算程序计算y的值,已知当输入x的值为-1时,输出y的值为3,则当输入x的值为3时,输出的y的值为__________.
图6
15.如图7①,在矩形ABCD中,BC=5,动点P从点B出发,沿折线BCDA匀速运动至点A停止.设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图7②所示,则DC=__________,y的最大值是__________.
图7
三、解答题(本大题共7小题,共75分)
16.(6分)已知一次函数y=kx+b的图象经过点A(2,-4)和点B(-1,5),求一次函数的解析式.
17.(8分)已知关于x的一次函数y=(3-m)x+m-5.
(1)若该一次函数的图象过原点,求实数m的值;
(2)当该一次函数的图象经过第二、三、四象限时,求实数m的取值范围.
18.(10分)下表给出了瓜农王大叔去年西瓜的销售额y(元)随卖出西瓜的质量x(千克)变化的几组数据:
质量x(千克) 1 2 3 4 5 6
销售额y(元) 2 4 6 8 10 12
(1)求去年西瓜的销售额y(元)关于卖出西瓜的质量x(千克)的函数解析式;
(2)求去年卖出20千克西瓜时的销售额.
19.(10分)如图8,已知直线l1:y1=x+b经过点A(-5,0),交y轴于点B,直线l2:y2=-2x-4与直线l1相交于点C,交y轴于点D.
(1)求b的值;
(2)求△BCD的面积;
(3)当0≤y2<y1时,x的取值范围是__________.
图8
20.(13分)为宣传“青少年身心全面发展”的理念,某游泳馆面向全体学生推出优惠活动,活动套餐如下:
套餐一:先购买会员卡,再购买门票打五折;
套餐二:不购买会员卡,直接购买门票打七五折.
若在此优惠活动期间购买一张会员卡的费用为40元,游泳x次,选择套餐一所需费用为y1元,且y1=k1x+b(k1≠0);选择套餐二所需费用为y2元,且y2=k2x(k2≠0),其函数图象如图9所示,回答下列问题.
(1)求k1和b的值;
(2)一张门票的原价为__________元;
(3)小明计划在优惠活动期间来此游泳馆游泳,请你通过计算,根据他到游泳馆游泳的次数情况,帮他分析出选择哪种套餐更合算?
图9
21.(13分)项目式学习:根据以下素材,探索完成任务.
制定销售方案
素材1 某商场推出了A,B两款运动鞋.一双A款运动鞋的售价比一双B款运动鞋的售价贵20元,购买1双A款运动鞋和2双B款运动鞋共需560元.
素材2 商场销售A款运动鞋共获利1 800元,销售B款运动鞋共获利2 000元,其中一双A款运动鞋的利润是一双B款运动鞋的 倍,A款运动鞋比B款运动鞋少卖10双.
问题解决
任务1 确定运动鞋的售价 一双A款运动鞋和一双B款运动鞋的售价各是多少?
任务2 确定运动鞋的进价 一双A款运动鞋和一双B款运动鞋的进价各是多少?(一双鞋的利润=一双鞋的售价-一双鞋的进价=)
任务3 拟定最佳销售方案 某企业欲购买运动鞋500双,已知购买A款运动鞋的数量不超过B款运动鞋数量的三倍,则该商场销售部如何配置运动鞋的数量,可以使得该笔交易获利最大?最大利润为多少?
22.(15分)如图10,在平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的函数解析式.
(2)点E是x轴上一动点,过点E作直线l⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G.若线段GF的长为3,求点G的坐标.
(3)在y轴上是否存在一点H,使得以O,C,H为顶点的三角形是等腰三角形?若存在,求出点H的坐标;若不存在,请说明理由.
图10 备用图
第十九章 限时检测卷
1.C 2.B 3.B 4.B 5.C 6.A 7.A 8.C 9.A 10.B
11.2 12.y=x+3(答案不唯一) 13.x>-1 14.1
15.6 15
16.解:将点A(2,-4),B(-1,5)代入y=kx+b,
得解得
∴一次函数的解析式为y=-3x+2.
17.解:(1)将原点(0,0)代入y=(3-m)x+m-5,
得m-5=0.解得m=5.
(2)由题意,得
解得3<m<5.
18.解:(1)由表格可知,y与x之间成正比例函数关系.
∴设y关于x的函数解析式为y=kx.
将(1,2)代入y=kx,得k=2.
∴y关于x的函数解析式为y=2x.
(2)当x=20时,y=2×20=40.
答:去年卖出20千克西瓜时的销售额为40元.
19.解:(1)把A(-5,0)代入y1=x+b,得-5+b=0.
解得b=5.
(2)由(1),得直线l1的函数解析式为y1=x+5.
当x=0时,y1=5.∴B(0,5).
联立直线l1与直线l2的解析式,
得解得
∴点C的坐标为(-3,2).
对于y2=-2x-4,令x=0,则y2=-4.∴D(0,-4).
∵B(0,5),∴BD=9.
∴S△BCD=BD·|xC|=×9×3=.
(3)-3<x≤-2.
20.解:(1)由图象可知,y1=k1x+b的图象过点(10,200),(0,40).
将(10,200),(0,40)代入y1=k1x+b,
得解得
(2)32.
(3)根据题意,得k2=32×0.75=24.∴y2=24x.
由(1),得k1=16,b=40.∴y1=16x+40.
当y1<y2时,16x+40<24x.解得x>5.
当y1=y2时,16x+40=24x.解得x=5.
当y1>y2时,16x+40>24x.解得x<5.
∴当他到游泳馆游泳的次数少于5时,选择套餐二更合算;当他到游泳馆游泳的次数等于5时,选择两种套餐一样合算;当他到游泳馆游泳的次数多于5时,选择套餐一更合算.
21.解:任务1:设一双A款运动鞋的售价是x元,则一双B款运动鞋的售价是(x-20)元.
根据题意,得x+2(x-20)=560.解得x=200.
∴x-20=180.
答:一双A款运动鞋的售价是200元,一双B款运动鞋的售价是180元.
任务2:设销售一双B款运动鞋的利润是m元,则销售一双A款运动鞋的利润是 m元.
根据题意,得=-10.解得m=50.
经检验,m=50是原方程的解,且符合题意.
∴m=60.
200-60=140(元),180-50=130(元).
答:一双A款运动鞋的进价是140元,一双B款运动鞋的进价是130元.
任务3:设商场销售部配置A款运动鞋t双,该笔交易获利w元.
∵购买A款运动鞋的数量不超过B款运动鞋数量的三倍,
∴t≤3(500-t).解得t≤375.
根据题意,得w=60t+50(500-t)=10t+25 000.
∵10>0,∴w随t的增大而增大.
∴当t=375时,w取最大值,最大值为10×375+25 000=28 750,此时500-t=125.
∴该商场销售部配置A款运动鞋375双,B款运动鞋125双,可以使得该笔交易获利最大,最大利润为28 750元.
22.解:(1)∵点C(a,4)在直线y=2x上,∴2a=4.解得a=2.
∴C(2,4).
将A(6,0),C(2,4)代入y=kx+b,
得解得
∴直线AB的函数解析式为y=-x+6.
(2)设点E的坐标为(m,0),则F(m,2m),G(m,-m+6).
∵线段GF的长为3,∴|2m-(-m+6)|=3.
解得m=3或m=1.
当m=3时,-m+6=3;当m=1时,-m+6=5.
∴点G的坐标为(3,3)或(1,5).
(3)存在.
设点H的坐标为(0,t),则OH=|t|.
∵C(2,4),∴OC==2,
CH==.
要使得以O,C,H为顶点的三角形是等腰三角形,可分为以下三种情况:
①当OC=OH时,|t|=2.解得t=±2.
∴点H的坐标为(0,2)或(0,-2).
②当OC=CH时,如答图1,过点C作CM⊥y轴于点M,则OM=HM.
答图1
∵C(2,4),∴OM=4.∴OH=2OM=8.
∴点H的坐标为(0,8).
③当CH=OH时,=|t|.
解得t=.∴点H的坐标为 .
综上所述,点H的坐标为(0,2)或(0,-2)或(0,8)或.
时间:100分钟 分值:120分 得分:__________
一、选择题(本大题共10小题,每小题3分,共30分)
1.在利用太阳能热水器加热水的过程中,热水器里的水温随所晒时间的长短而变化,在这个问题中,自变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
2.函数y=的自变量x的取值范围是( )
A.x≥2 B.x≤2 C.x≥-2 D.x≤-2
3.一次函数y=-2x+6的图象与x轴的交点坐标是( )
A.(0,3) B.(3,0) C.(0,6) D.(6,0)
4.把直线y=-x-5向下平移3个单位长度得到直线l,则直线l对应的解析式是( )
A.y=-x-2 B.y=-x-8 C.y=3x-5 D.y=-3x-8
5.若函数y=(m-1)x|m|-5是关于x的一次函数,则m的值为( )
A.±1 B.1 C.-1 D.2
6.一次函数y=kx+b的图象如图1所示,则k,b的取值范围是( )
图1
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
7.已知点(-1,y1),(2,y2)在直线y=-x+b上,则y1,y2的大小关系是( )
A.y1>y2 B.y1
图2
A. B. C. D.
9.图3是一款上下细中间粗的茶杯,向该茶杯中匀速注水,下列图象能大致反映茶杯中水面的高度h与注水时间t的关系的是( )
10.如图4,在平面直角坐标系xOy中,点A1(1,1)在直线y=x上,过点A1作y轴的平行线,交直线y=-x于点B1,以线段A1B1为边在右侧作正方形A1B1C1D1,C1D1所在的直线交直线y=x于点A2,交直线y=-x于点B2,再以线段A2B2为边在右侧作正方形A2B2C2D2,……按照此规律依次类推,点A8的横坐标为( )
图4
A.38 B.37 C.37-1 D.38-1
二、填空题(本大题共5小题,每小题3分,共15分)
11.若点(3,a)在一次函数y=-x+3的图象上,则a的值为__________.
12.若一次函数的图象过点(2,5),且y随x的增大而增大,请写出一个满足上述条件的函数解析式:__________.
13.如图5,一次函数y=kx+b的图象经过点P(-1,3),则关于x的不等式kx+b<3的解集为__________.
图5
14.按照如图6所示的运算程序计算y的值,已知当输入x的值为-1时,输出y的值为3,则当输入x的值为3时,输出的y的值为__________.
图6
15.如图7①,在矩形ABCD中,BC=5,动点P从点B出发,沿折线BCDA匀速运动至点A停止.设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图7②所示,则DC=__________,y的最大值是__________.
图7
三、解答题(本大题共7小题,共75分)
16.(6分)已知一次函数y=kx+b的图象经过点A(2,-4)和点B(-1,5),求一次函数的解析式.
17.(8分)已知关于x的一次函数y=(3-m)x+m-5.
(1)若该一次函数的图象过原点,求实数m的值;
(2)当该一次函数的图象经过第二、三、四象限时,求实数m的取值范围.
18.(10分)下表给出了瓜农王大叔去年西瓜的销售额y(元)随卖出西瓜的质量x(千克)变化的几组数据:
质量x(千克) 1 2 3 4 5 6
销售额y(元) 2 4 6 8 10 12
(1)求去年西瓜的销售额y(元)关于卖出西瓜的质量x(千克)的函数解析式;
(2)求去年卖出20千克西瓜时的销售额.
19.(10分)如图8,已知直线l1:y1=x+b经过点A(-5,0),交y轴于点B,直线l2:y2=-2x-4与直线l1相交于点C,交y轴于点D.
(1)求b的值;
(2)求△BCD的面积;
(3)当0≤y2<y1时,x的取值范围是__________.
图8
20.(13分)为宣传“青少年身心全面发展”的理念,某游泳馆面向全体学生推出优惠活动,活动套餐如下:
套餐一:先购买会员卡,再购买门票打五折;
套餐二:不购买会员卡,直接购买门票打七五折.
若在此优惠活动期间购买一张会员卡的费用为40元,游泳x次,选择套餐一所需费用为y1元,且y1=k1x+b(k1≠0);选择套餐二所需费用为y2元,且y2=k2x(k2≠0),其函数图象如图9所示,回答下列问题.
(1)求k1和b的值;
(2)一张门票的原价为__________元;
(3)小明计划在优惠活动期间来此游泳馆游泳,请你通过计算,根据他到游泳馆游泳的次数情况,帮他分析出选择哪种套餐更合算?
图9
21.(13分)项目式学习:根据以下素材,探索完成任务.
制定销售方案
素材1 某商场推出了A,B两款运动鞋.一双A款运动鞋的售价比一双B款运动鞋的售价贵20元,购买1双A款运动鞋和2双B款运动鞋共需560元.
素材2 商场销售A款运动鞋共获利1 800元,销售B款运动鞋共获利2 000元,其中一双A款运动鞋的利润是一双B款运动鞋的 倍,A款运动鞋比B款运动鞋少卖10双.
问题解决
任务1 确定运动鞋的售价 一双A款运动鞋和一双B款运动鞋的售价各是多少?
任务2 确定运动鞋的进价 一双A款运动鞋和一双B款运动鞋的进价各是多少?(一双鞋的利润=一双鞋的售价-一双鞋的进价=)
任务3 拟定最佳销售方案 某企业欲购买运动鞋500双,已知购买A款运动鞋的数量不超过B款运动鞋数量的三倍,则该商场销售部如何配置运动鞋的数量,可以使得该笔交易获利最大?最大利润为多少?
22.(15分)如图10,在平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的函数解析式.
(2)点E是x轴上一动点,过点E作直线l⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G.若线段GF的长为3,求点G的坐标.
(3)在y轴上是否存在一点H,使得以O,C,H为顶点的三角形是等腰三角形?若存在,求出点H的坐标;若不存在,请说明理由.
图10 备用图
第十九章 限时检测卷
1.C 2.B 3.B 4.B 5.C 6.A 7.A 8.C 9.A 10.B
11.2 12.y=x+3(答案不唯一) 13.x>-1 14.1
15.6 15
16.解:将点A(2,-4),B(-1,5)代入y=kx+b,
得解得
∴一次函数的解析式为y=-3x+2.
17.解:(1)将原点(0,0)代入y=(3-m)x+m-5,
得m-5=0.解得m=5.
(2)由题意,得
解得3<m<5.
18.解:(1)由表格可知,y与x之间成正比例函数关系.
∴设y关于x的函数解析式为y=kx.
将(1,2)代入y=kx,得k=2.
∴y关于x的函数解析式为y=2x.
(2)当x=20时,y=2×20=40.
答:去年卖出20千克西瓜时的销售额为40元.
19.解:(1)把A(-5,0)代入y1=x+b,得-5+b=0.
解得b=5.
(2)由(1),得直线l1的函数解析式为y1=x+5.
当x=0时,y1=5.∴B(0,5).
联立直线l1与直线l2的解析式,
得解得
∴点C的坐标为(-3,2).
对于y2=-2x-4,令x=0,则y2=-4.∴D(0,-4).
∵B(0,5),∴BD=9.
∴S△BCD=BD·|xC|=×9×3=.
(3)-3<x≤-2.
20.解:(1)由图象可知,y1=k1x+b的图象过点(10,200),(0,40).
将(10,200),(0,40)代入y1=k1x+b,
得解得
(2)32.
(3)根据题意,得k2=32×0.75=24.∴y2=24x.
由(1),得k1=16,b=40.∴y1=16x+40.
当y1<y2时,16x+40<24x.解得x>5.
当y1=y2时,16x+40=24x.解得x=5.
当y1>y2时,16x+40>24x.解得x<5.
∴当他到游泳馆游泳的次数少于5时,选择套餐二更合算;当他到游泳馆游泳的次数等于5时,选择两种套餐一样合算;当他到游泳馆游泳的次数多于5时,选择套餐一更合算.
21.解:任务1:设一双A款运动鞋的售价是x元,则一双B款运动鞋的售价是(x-20)元.
根据题意,得x+2(x-20)=560.解得x=200.
∴x-20=180.
答:一双A款运动鞋的售价是200元,一双B款运动鞋的售价是180元.
任务2:设销售一双B款运动鞋的利润是m元,则销售一双A款运动鞋的利润是 m元.
根据题意,得=-10.解得m=50.
经检验,m=50是原方程的解,且符合题意.
∴m=60.
200-60=140(元),180-50=130(元).
答:一双A款运动鞋的进价是140元,一双B款运动鞋的进价是130元.
任务3:设商场销售部配置A款运动鞋t双,该笔交易获利w元.
∵购买A款运动鞋的数量不超过B款运动鞋数量的三倍,
∴t≤3(500-t).解得t≤375.
根据题意,得w=60t+50(500-t)=10t+25 000.
∵10>0,∴w随t的增大而增大.
∴当t=375时,w取最大值,最大值为10×375+25 000=28 750,此时500-t=125.
∴该商场销售部配置A款运动鞋375双,B款运动鞋125双,可以使得该笔交易获利最大,最大利润为28 750元.
22.解:(1)∵点C(a,4)在直线y=2x上,∴2a=4.解得a=2.
∴C(2,4).
将A(6,0),C(2,4)代入y=kx+b,
得解得
∴直线AB的函数解析式为y=-x+6.
(2)设点E的坐标为(m,0),则F(m,2m),G(m,-m+6).
∵线段GF的长为3,∴|2m-(-m+6)|=3.
解得m=3或m=1.
当m=3时,-m+6=3;当m=1时,-m+6=5.
∴点G的坐标为(3,3)或(1,5).
(3)存在.
设点H的坐标为(0,t),则OH=|t|.
∵C(2,4),∴OC==2,
CH==.
要使得以O,C,H为顶点的三角形是等腰三角形,可分为以下三种情况:
①当OC=OH时,|t|=2.解得t=±2.
∴点H的坐标为(0,2)或(0,-2).
②当OC=CH时,如答图1,过点C作CM⊥y轴于点M,则OM=HM.
答图1
∵C(2,4),∴OM=4.∴OH=2OM=8.
∴点H的坐标为(0,8).
③当CH=OH时,=|t|.
解得t=.∴点H的坐标为 .
综上所述,点H的坐标为(0,2)或(0,-2)或(0,8)或.
