第十七章勾股定理 限时检测卷 (含答案) 2024-2025学年数学人教版八年级下册
文档属性
| 名称 | 第十七章勾股定理 限时检测卷 (含答案) 2024-2025学年数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 189.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 16:22:59 | ||
图片预览


文档简介
第十七章勾股定理 限时检测卷
时间:100分钟 分值:120分 得分:__________
一、选择题(本大题共10小题,每小题3分,共30分)
1.若一个直角三角形的两条直角边的长分别是5和12,则斜边的长为( )
A.13 B. C.7或17 D.13或
2.在平面直角坐标系xOy中,点P(1,)到原点O的距离是( )
A. B.2 C.3 D.4
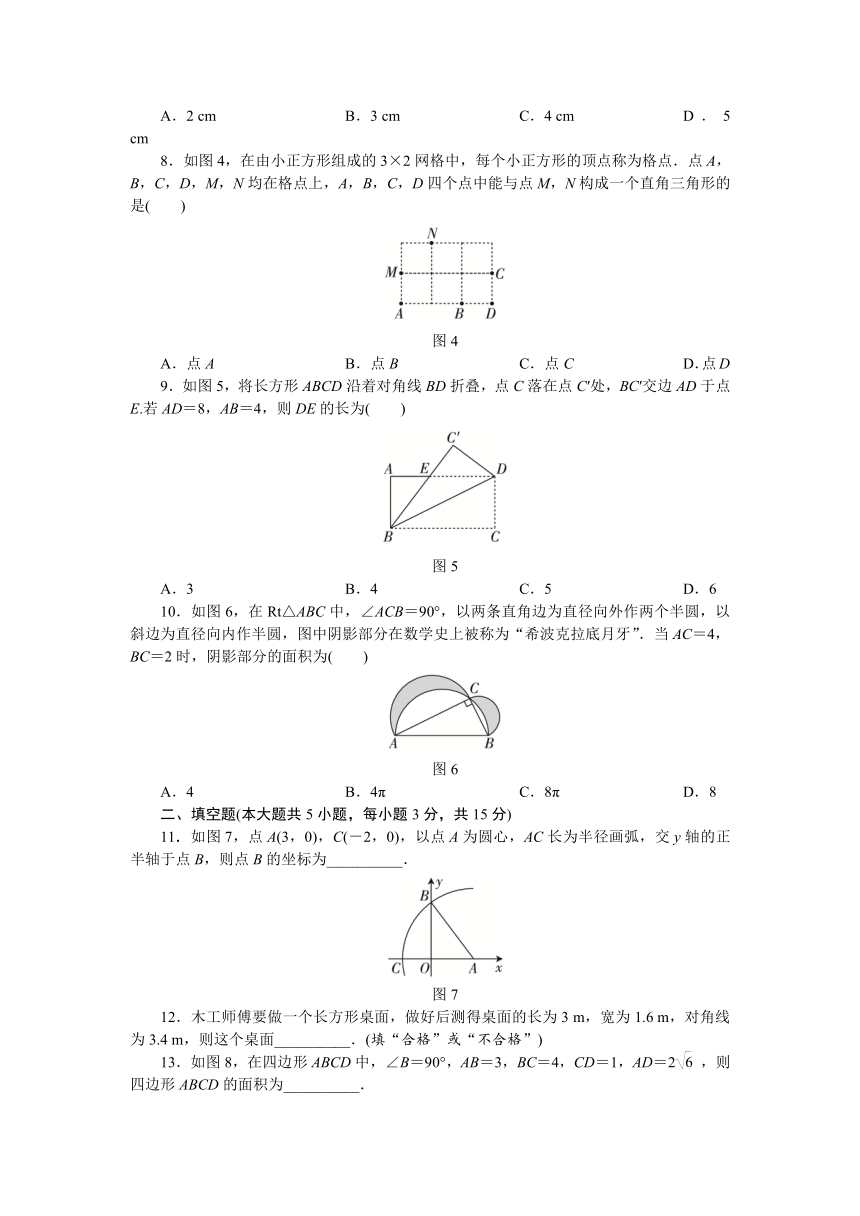
3.如图1,点O在数轴上表示的数为0,在数轴上取一点A,使OA=5,过点A作直线l⊥OA,在直线l上取点B,使AB=2,以点O为圆心,OB长为半径作弧,交数轴正半轴于点C,则点C表示的数是( )
图1
A. B. C.7 D.29
4.以下列各数为边长,能构造成直角三角形的是( )
A.0.1,0.2,0.3 B.,,2 C.6,7,8 D.9,40,41
5.如图2,某自动感应门的正上方A处装着一个感应器,离地面的高度AB为2.5 m.当一名学生站在C处时,感应门自动打开,此时这名学生到感应门的距离BC为1.2 m,头顶到感应器的距离AD为1.5 m,则这名学生的身高CD为( )
图2
A.0.9 m B.1.3 m C.1.5 m D.1.6 m
6.下列命题的逆命题是真命题的是( )
A.若a=b,则|a|=|b| B.全等三角形的周长相等
C.若a=0,则ab=0 D.有两边相等的三角形是等腰三角形
7.如图3,将长为8 cm的橡皮筋放置在水平面上,固定两端点A和B,然后把AB的中点C垂直向上拉升3 cm至点D,则橡皮筋被拉长了( )
图3
A.2 cm B.3 cm C.4 cm D.5 cm
8.如图4,在由小正方形组成的3×2网格中,每个小正方形的顶点称为格点.点A,B,C,D,M,N均在格点上,A,B,C,D四个点中能与点M,N构成一个直角三角形的是( )
图4
A.点A B.点B C.点C D.点D
9.如图5,将长方形ABCD沿着对角线BD折叠,点C落在点C′处,BC′交边AD于点E.若AD=8,AB=4,则DE的长为( )
图5
A.3 B.4 C.5 D.6
10.如图6,在Rt△ABC中,∠ACB=90°,以两条直角边为直径向外作两个半圆,以斜边为直径向内作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=4,BC=2时,阴影部分的面积为( )
图6
A.4 B.4π C.8π D.8
二、填空题(本大题共5小题,每小题3分,共15分)
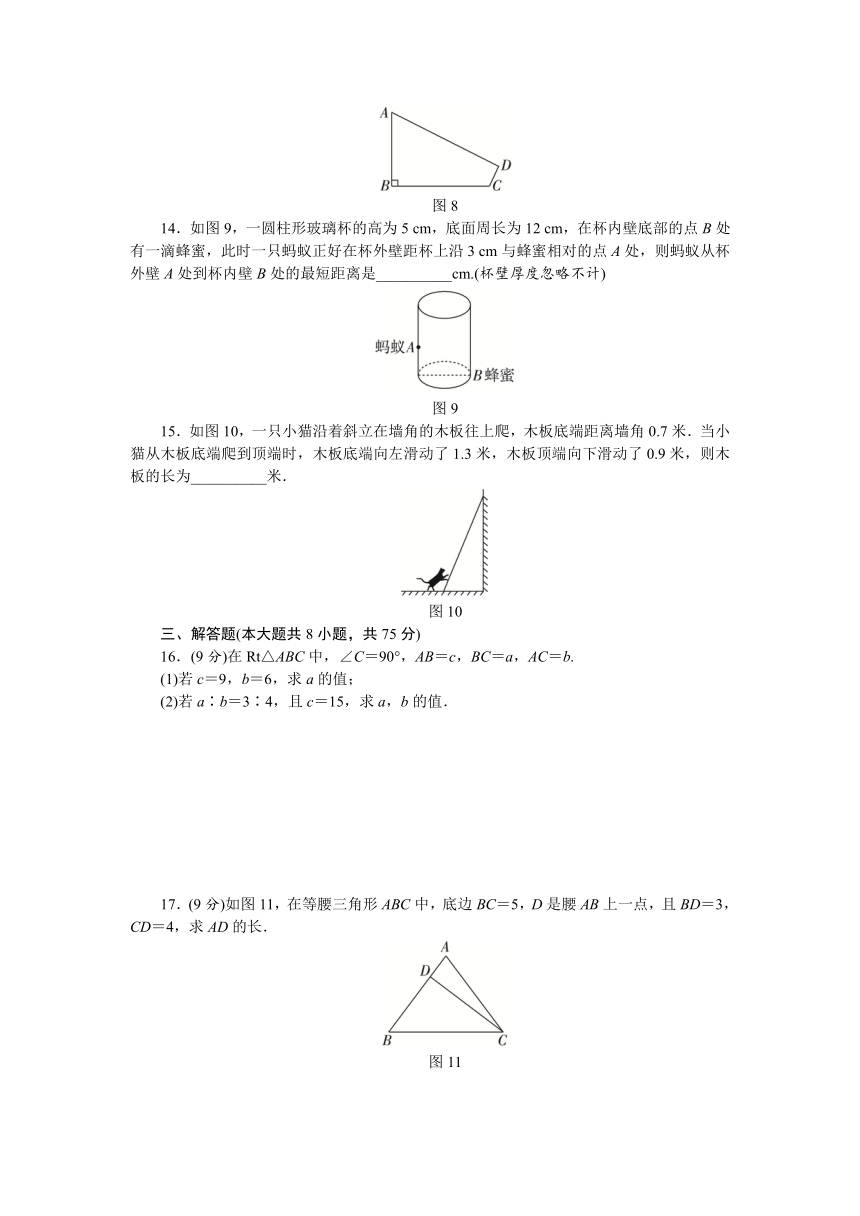
11.如图7,点A(3,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴的正半轴于点B,则点B的坐标为__________.
图7
12.木工师傅要做一个长方形桌面,做好后测得桌面的长为3 m,宽为1.6 m,对角线为3.4 m,则这个桌面__________.(填“合格”或“不合格”)
13.如图8,在四边形ABCD中,∠B=90°,AB=3,BC=4,CD=1,AD=2,则四边形ABCD的面积为__________.
图8
14.如图9,一圆柱形玻璃杯的高为5 cm,底面周长为12 cm,在杯内壁底部的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁距杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从杯外壁A处到杯内壁B处的最短距离是__________cm.(杯壁厚度忽略不计)
图9
15.如图10,一只小猫沿着斜立在墙角的木板往上爬,木板底端距离墙角0.7米.当小猫从木板底端爬到顶端时,木板底端向左滑动了1.3米,木板顶端向下滑动了0.9米,则木板的长为__________米.
图10
三、解答题(本大题共8小题,共75分)
16.(9分)在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)若c=9,b=6,求a的值;
(2)若a∶b=3∶4,且c=15,求a,b的值.
17.(9分)如图11,在等腰三角形ABC中,底边BC=5,D是腰AB上一点,且BD=3,CD=4,求AD的长.
图11
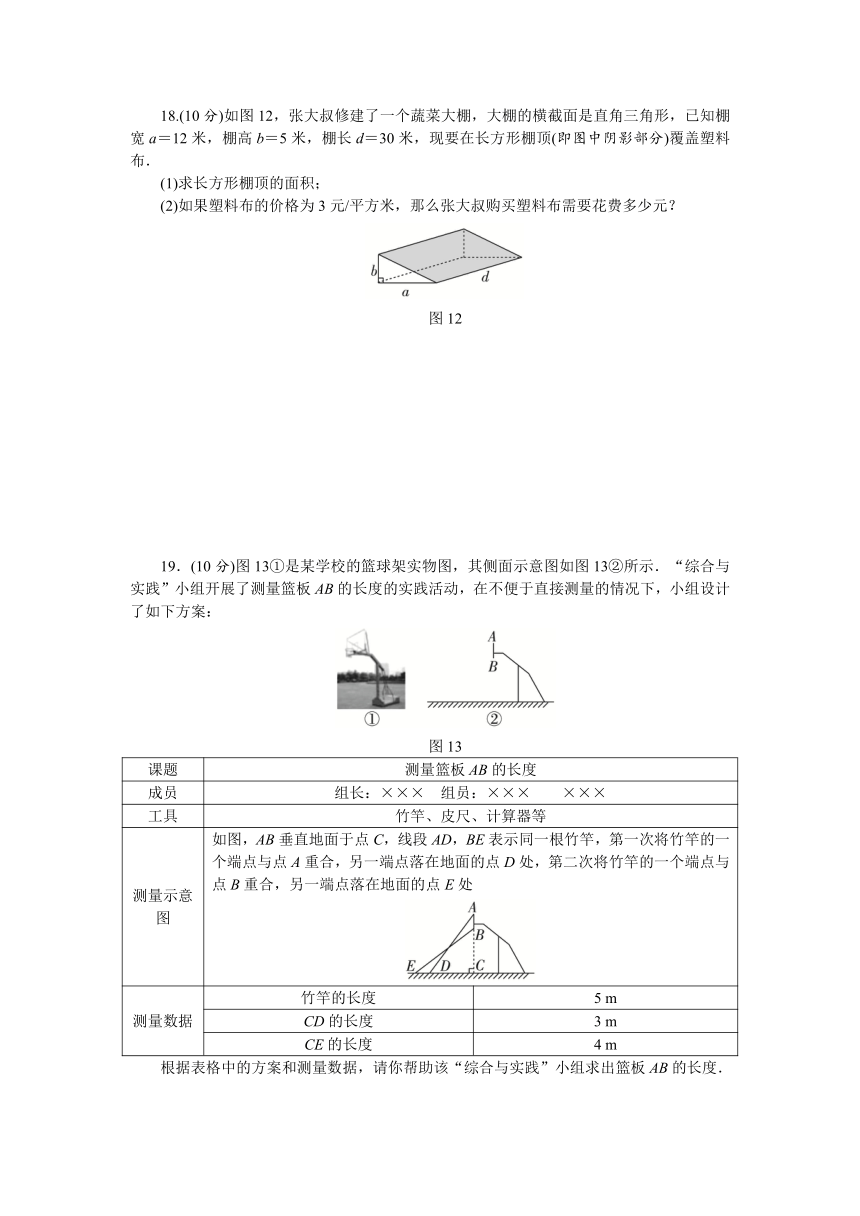
18.(10分)如图12,张大叔修建了一个蔬菜大棚,大棚的横截面是直角三角形,已知棚宽a=12米,棚高b=5米,棚长d=30米,现要在长方形棚顶(即图中阴影部分)覆盖塑料布.
(1)求长方形棚顶的面积;
(2)如果塑料布的价格为3元/平方米,那么张大叔购买塑料布需要花费多少元?
图12
19.(10分)图13①是某学校的篮球架实物图,其侧面示意图如图13②所示.“综合与实践”小组开展了测量篮板AB的长度的实践活动,在不便于直接测量的情况下,小组设计了如下方案:
图13
课题 测量篮板AB的长度
成员 组长:××× 组员:××× ×××
工具 竹竿、皮尺、计算器等
测量示意图 如图,AB垂直地面于点C,线段AD,BE表示同一根竹竿,第一次将竹竿的一个端点与点A重合,另一端点落在地面的点D处,第二次将竹竿的一个端点与点B重合,另一端点落在地面的点E处
测量数据 竹竿的长度 5 m
CD的长度 3 m
CE的长度 4 m
根据表格中的方案和测量数据,请你帮助该“综合与实践”小组求出篮板AB的长度.
20.(12分)如图14,在△ABC中,D是边BC的中点,DE⊥BC交AB于点E,且BE2-AE2=AC2.
(1)求证:∠A=90°;
(2)若AC=6,BD=5,求AE的长.
图14
21.(12分)清代数学家罗士琳痴迷研究勾股定理,提出推算勾股数的“罗士琳法则”,其中有一个法则是“如果k是大于2的偶数,那么k,k的一半的平方减1,k的一半的平方加1是一组勾股数”.
(1)当k=14时,写出这一组勾股数:__________.
(2)证明“罗士琳法则”的正确性.
22.(13分)如图15,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q分别是△ABC边AB,BC上的两个动点,点P从点A出发,沿AB方向运动,且速度为1 cm/s,同时点Q从点B出发,沿BC方向运动,且速度为2 cm/s.设运动的时间为t s.
(1)连接PQ,当t=2时,求PQ的长;
(2)若点Q从点B出发,沿折线BCA运动,速度不变,则当t为何值时,点Q在边CA上,且△BCQ是等腰三角形?
图15
第十七章 限时检测卷
1.A 2.B 3.B 4.D 5.D 6.D 7.A 8.D 9.C 10.A
11.(0,4) 12.合格 13.6+ 14.10 15.2.5
16.解:(1)在Rt△ABC中,∠C=90°,
∴a===3.
(2)设a=3x,则b=4x.
由勾股定理,得a2+b2=c2,即(3x)2+(4x)2=152.
解得x=3(负值已舍).
∴a=9,b=12.
17.解:设AB=AC=a,则AD=a-3.
∵BC=5,CD=4,BD=3,∴BD2+CD2=BC2.
∴∠BDC=90°.∴∠ADC=90°.
在Rt△ADC中,由勾股定理,得AD2+CD2=AC2.
∴(a-3)2+42=a2.解得a=.
∴AD=a-3=-3=.
18.解:(1)根据题意,由勾股定理,得棚顶的斜宽为==13(米).
13×30=390(平方米).
答:长方形棚顶的面积为390平方米.
(2)390×3=1 170(元).
答:张大叔购买塑料布需要花费1 170元.
19.解:在Rt△ADC中,由勾股定理,得AC===4(m).
在Rt△BEC中,由勾股定理,得BC===3(m).
∴AB=AC-BC=4-3=1(m).
答:学校篮板AB的长度为1 m.
20.(1)证明:如答图1,连接CE.
答图1
∵D是边BC的中点,DE⊥BC,
∴DE垂直平分BC.
∴CE=BE.
∵BE2-AE2=AC2,
∴CE2-AE2=AC2,
即AC2+AE2=CE2.
∴∠A=90°.
(2)解:∵D是边BC的中点,BD=5,∴BC=2BD=10.
∵∠A=90°,AC=6,
∴AB===8.
∴CE=BE=AB-AE=8-AE.
在Rt△AEC中,由勾股定理,得AC2+AE2=CE2,
即62+AE2=(8-AE)2.
解得AE=.∴AE的长为 .
21.(1)解:14 48 50.
(2)证明:k2+=k2+=k2+k4-k2+1=k4+k2+1.
==k4+k2+1.
∴k2+=.
当k是大于2的偶数时,-1,+1是正整数.
∴如果k是大于2的偶数,那么k,k的一半的平方减1,k的一半的平方加1是一组勾股数.
22.解:(1)当t=2时,BQ=2×2=4(cm),AP=1×2=2(cm).
∴BP=AB-AP=8-2=6(cm).
在Rt△BPQ中,∠B=90°,由勾股定理,
得PQ===2(cm).
(2)分以下三种情况:
①如答图2,当CQ=BQ,即∠C=∠CBQ时,∵∠ABC=90°,
答图2
∴∠CBQ+∠ABQ=90°,∠A+∠C=90°.
∴∠A=∠ABQ.∴AQ=BQ.
∴CQ=AQ.
∵∠ABC=90°,AB=8 cm,BC=6 cm,
∴AC===10(cm).
∴CQ=AQ=AC=5 cm.∴BC+CQ=11 cm.
∴t=11÷2=5.5.
②如答图3,当CQ=BC时,BC+CQ=2BC=12 cm.
答图3
∴t=12÷2=6.
③如答图4,当BC=BQ时,过点B作BE⊥AC于点E.
答图4
∵S△ABC=AB·BC=AC·BE,
∴BE===4.8(cm).
∴CE===3.6(cm).
∵BC=BQ,BE⊥AC,∴CQ=2CE=7.2 cm.
∴BC+CQ=13.2 cm.∴t=13.2÷2=6.6.
综上所述,当t的值为5.5或6或6.6时,点Q在边CA上,且△BCQ是等腰三角形.
时间:100分钟 分值:120分 得分:__________
一、选择题(本大题共10小题,每小题3分,共30分)
1.若一个直角三角形的两条直角边的长分别是5和12,则斜边的长为( )
A.13 B. C.7或17 D.13或
2.在平面直角坐标系xOy中,点P(1,)到原点O的距离是( )
A. B.2 C.3 D.4
3.如图1,点O在数轴上表示的数为0,在数轴上取一点A,使OA=5,过点A作直线l⊥OA,在直线l上取点B,使AB=2,以点O为圆心,OB长为半径作弧,交数轴正半轴于点C,则点C表示的数是( )
图1
A. B. C.7 D.29
4.以下列各数为边长,能构造成直角三角形的是( )
A.0.1,0.2,0.3 B.,,2 C.6,7,8 D.9,40,41
5.如图2,某自动感应门的正上方A处装着一个感应器,离地面的高度AB为2.5 m.当一名学生站在C处时,感应门自动打开,此时这名学生到感应门的距离BC为1.2 m,头顶到感应器的距离AD为1.5 m,则这名学生的身高CD为( )
图2
A.0.9 m B.1.3 m C.1.5 m D.1.6 m
6.下列命题的逆命题是真命题的是( )
A.若a=b,则|a|=|b| B.全等三角形的周长相等
C.若a=0,则ab=0 D.有两边相等的三角形是等腰三角形
7.如图3,将长为8 cm的橡皮筋放置在水平面上,固定两端点A和B,然后把AB的中点C垂直向上拉升3 cm至点D,则橡皮筋被拉长了( )
图3
A.2 cm B.3 cm C.4 cm D.5 cm
8.如图4,在由小正方形组成的3×2网格中,每个小正方形的顶点称为格点.点A,B,C,D,M,N均在格点上,A,B,C,D四个点中能与点M,N构成一个直角三角形的是( )
图4
A.点A B.点B C.点C D.点D
9.如图5,将长方形ABCD沿着对角线BD折叠,点C落在点C′处,BC′交边AD于点E.若AD=8,AB=4,则DE的长为( )
图5
A.3 B.4 C.5 D.6
10.如图6,在Rt△ABC中,∠ACB=90°,以两条直角边为直径向外作两个半圆,以斜边为直径向内作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=4,BC=2时,阴影部分的面积为( )
图6
A.4 B.4π C.8π D.8
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图7,点A(3,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴的正半轴于点B,则点B的坐标为__________.
图7
12.木工师傅要做一个长方形桌面,做好后测得桌面的长为3 m,宽为1.6 m,对角线为3.4 m,则这个桌面__________.(填“合格”或“不合格”)
13.如图8,在四边形ABCD中,∠B=90°,AB=3,BC=4,CD=1,AD=2,则四边形ABCD的面积为__________.
图8
14.如图9,一圆柱形玻璃杯的高为5 cm,底面周长为12 cm,在杯内壁底部的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁距杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从杯外壁A处到杯内壁B处的最短距离是__________cm.(杯壁厚度忽略不计)
图9
15.如图10,一只小猫沿着斜立在墙角的木板往上爬,木板底端距离墙角0.7米.当小猫从木板底端爬到顶端时,木板底端向左滑动了1.3米,木板顶端向下滑动了0.9米,则木板的长为__________米.
图10
三、解答题(本大题共8小题,共75分)
16.(9分)在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)若c=9,b=6,求a的值;
(2)若a∶b=3∶4,且c=15,求a,b的值.
17.(9分)如图11,在等腰三角形ABC中,底边BC=5,D是腰AB上一点,且BD=3,CD=4,求AD的长.
图11
18.(10分)如图12,张大叔修建了一个蔬菜大棚,大棚的横截面是直角三角形,已知棚宽a=12米,棚高b=5米,棚长d=30米,现要在长方形棚顶(即图中阴影部分)覆盖塑料布.
(1)求长方形棚顶的面积;
(2)如果塑料布的价格为3元/平方米,那么张大叔购买塑料布需要花费多少元?
图12
19.(10分)图13①是某学校的篮球架实物图,其侧面示意图如图13②所示.“综合与实践”小组开展了测量篮板AB的长度的实践活动,在不便于直接测量的情况下,小组设计了如下方案:
图13
课题 测量篮板AB的长度
成员 组长:××× 组员:××× ×××
工具 竹竿、皮尺、计算器等
测量示意图 如图,AB垂直地面于点C,线段AD,BE表示同一根竹竿,第一次将竹竿的一个端点与点A重合,另一端点落在地面的点D处,第二次将竹竿的一个端点与点B重合,另一端点落在地面的点E处
测量数据 竹竿的长度 5 m
CD的长度 3 m
CE的长度 4 m
根据表格中的方案和测量数据,请你帮助该“综合与实践”小组求出篮板AB的长度.
20.(12分)如图14,在△ABC中,D是边BC的中点,DE⊥BC交AB于点E,且BE2-AE2=AC2.
(1)求证:∠A=90°;
(2)若AC=6,BD=5,求AE的长.
图14
21.(12分)清代数学家罗士琳痴迷研究勾股定理,提出推算勾股数的“罗士琳法则”,其中有一个法则是“如果k是大于2的偶数,那么k,k的一半的平方减1,k的一半的平方加1是一组勾股数”.
(1)当k=14时,写出这一组勾股数:__________.
(2)证明“罗士琳法则”的正确性.
22.(13分)如图15,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q分别是△ABC边AB,BC上的两个动点,点P从点A出发,沿AB方向运动,且速度为1 cm/s,同时点Q从点B出发,沿BC方向运动,且速度为2 cm/s.设运动的时间为t s.
(1)连接PQ,当t=2时,求PQ的长;
(2)若点Q从点B出发,沿折线BCA运动,速度不变,则当t为何值时,点Q在边CA上,且△BCQ是等腰三角形?
图15
第十七章 限时检测卷
1.A 2.B 3.B 4.D 5.D 6.D 7.A 8.D 9.C 10.A
11.(0,4) 12.合格 13.6+ 14.10 15.2.5
16.解:(1)在Rt△ABC中,∠C=90°,
∴a===3.
(2)设a=3x,则b=4x.
由勾股定理,得a2+b2=c2,即(3x)2+(4x)2=152.
解得x=3(负值已舍).
∴a=9,b=12.
17.解:设AB=AC=a,则AD=a-3.
∵BC=5,CD=4,BD=3,∴BD2+CD2=BC2.
∴∠BDC=90°.∴∠ADC=90°.
在Rt△ADC中,由勾股定理,得AD2+CD2=AC2.
∴(a-3)2+42=a2.解得a=.
∴AD=a-3=-3=.
18.解:(1)根据题意,由勾股定理,得棚顶的斜宽为==13(米).
13×30=390(平方米).
答:长方形棚顶的面积为390平方米.
(2)390×3=1 170(元).
答:张大叔购买塑料布需要花费1 170元.
19.解:在Rt△ADC中,由勾股定理,得AC===4(m).
在Rt△BEC中,由勾股定理,得BC===3(m).
∴AB=AC-BC=4-3=1(m).
答:学校篮板AB的长度为1 m.
20.(1)证明:如答图1,连接CE.
答图1
∵D是边BC的中点,DE⊥BC,
∴DE垂直平分BC.
∴CE=BE.
∵BE2-AE2=AC2,
∴CE2-AE2=AC2,
即AC2+AE2=CE2.
∴∠A=90°.
(2)解:∵D是边BC的中点,BD=5,∴BC=2BD=10.
∵∠A=90°,AC=6,
∴AB===8.
∴CE=BE=AB-AE=8-AE.
在Rt△AEC中,由勾股定理,得AC2+AE2=CE2,
即62+AE2=(8-AE)2.
解得AE=.∴AE的长为 .
21.(1)解:14 48 50.
(2)证明:k2+=k2+=k2+k4-k2+1=k4+k2+1.
==k4+k2+1.
∴k2+=.
当k是大于2的偶数时,-1,+1是正整数.
∴如果k是大于2的偶数,那么k,k的一半的平方减1,k的一半的平方加1是一组勾股数.
22.解:(1)当t=2时,BQ=2×2=4(cm),AP=1×2=2(cm).
∴BP=AB-AP=8-2=6(cm).
在Rt△BPQ中,∠B=90°,由勾股定理,
得PQ===2(cm).
(2)分以下三种情况:
①如答图2,当CQ=BQ,即∠C=∠CBQ时,∵∠ABC=90°,
答图2
∴∠CBQ+∠ABQ=90°,∠A+∠C=90°.
∴∠A=∠ABQ.∴AQ=BQ.
∴CQ=AQ.
∵∠ABC=90°,AB=8 cm,BC=6 cm,
∴AC===10(cm).
∴CQ=AQ=AC=5 cm.∴BC+CQ=11 cm.
∴t=11÷2=5.5.
②如答图3,当CQ=BC时,BC+CQ=2BC=12 cm.
答图3
∴t=12÷2=6.
③如答图4,当BC=BQ时,过点B作BE⊥AC于点E.
答图4
∵S△ABC=AB·BC=AC·BE,
∴BE===4.8(cm).
∴CE===3.6(cm).
∵BC=BQ,BE⊥AC,∴CQ=2CE=7.2 cm.
∴BC+CQ=13.2 cm.∴t=13.2÷2=6.6.
综上所述,当t的值为5.5或6或6.6时,点Q在边CA上,且△BCQ是等腰三角形.
