旋转和折叠重点考点单选题 归类练 2025年中考数学一轮复习备考
文档属性
| 名称 | 旋转和折叠重点考点单选题 归类练 2025年中考数学一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 16:53:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
旋转和折叠重点考点单选题 归类练
2025年中考数学一轮复习备考
一、单选题
1.如图,在矩形ABCD中,点E、F分别在边AB、BC上,且,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:
①;②≌;
③;④.
其中正确的结论是( ).
A.①②③④ B.①②③ C.②③④ D.①③④
2.如图,在矩形ABCD中,对角线AC,BD交于点O,,点E在边AD上,,点F在边BC上,将四边形CDEF沿EF所在的直线翻折,点D恰好落在点O处,点C落在点处.下列结论中,正确的有( )
①;②过点O作于点P,是等腰直角三角形;③AB的长为
A.3个 B.2个 C.0个 D.1个
3.如图,四边形是矩形纸片,.对折矩形纸片,使与重合,折痕为;展平后再过点B折叠矩形纸片,使点A落在上的点N,折痕与相交于点Q;再次展平,连接,,延长交于点G.有如下结论:①;②;③;④是等边三角形;⑤点P为线段上一动点,点H是的中点,则的最小值是.其中正确结论有( )
A.5个 B.4个 C.3个 D.2个
4.如图,在矩形中,点M在边上,先将矩形纸片沿所在的直线折叠,使点D落在点处,与交于点N.之后再将矩形纸片折叠,使恰好落在直线上,点A落在点处,点B落在点处,折痕为.若,,则的长为( )
A.6 B.8 C.10 D.12
5.如图,在矩形中,,分别是边,上的点,且,将矩形沿折叠,点恰好落在边上点处,再将沿折叠,点恰好落在上的点处.若,,则的长为( )
A. B. C. D.
6.如图,点E是矩形边上一点,连接,将沿翻折,点落在点处,的角平分线与的延长线交于点,若,,当点从点运动到点时,则点运动的路径长是( )
A. B. C. D.
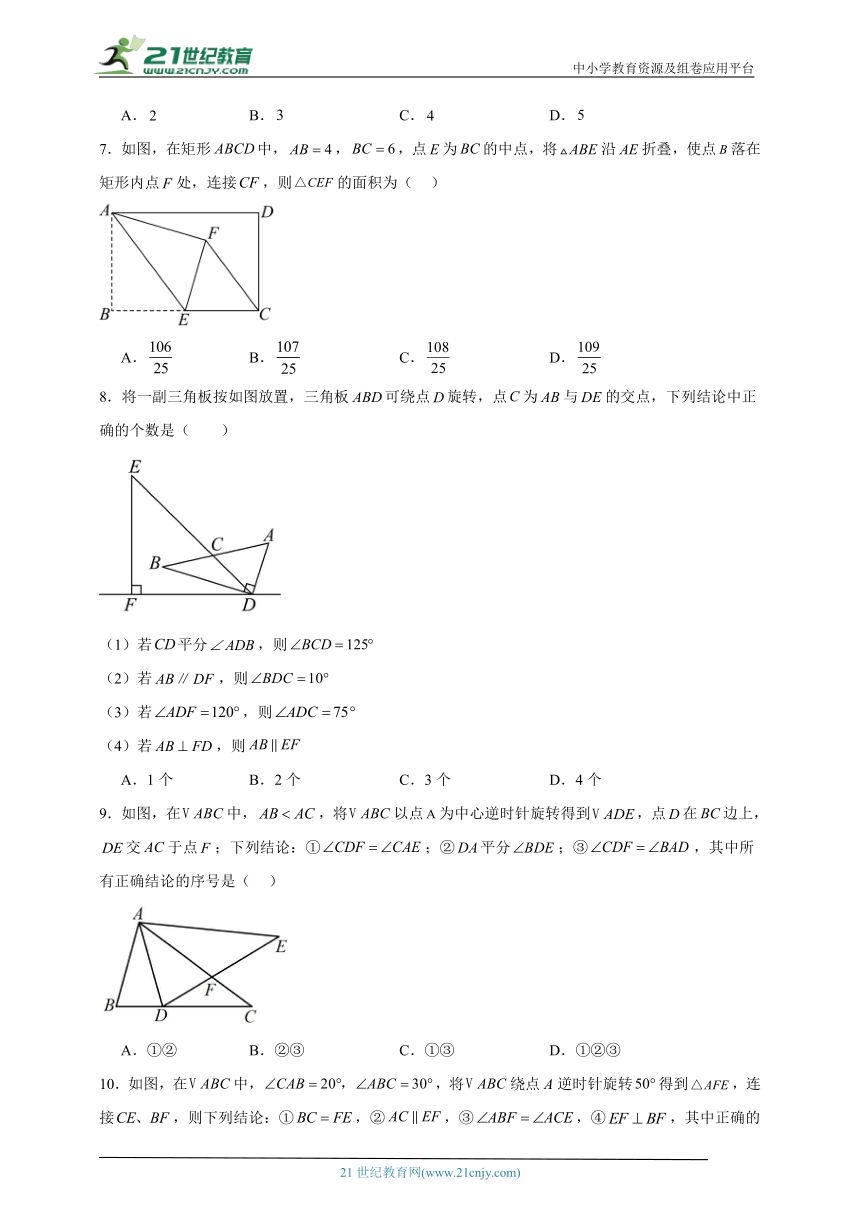
7.如图,在矩形中,,,点为的中点,将沿折叠,使点落在矩形内点处,连接,则的面积为( )
A. B. C. D.
8.将一副三角板按如图放置,三角板可绕点旋转,点为与的交点,下列结论中正确的个数是( )
(1)若平分,则
(2)若,则
(3)若,则
(4)若,则
A.1个 B.2个 C.3个 D.4个
9.如图,在中,,将以点为中心逆时针旋转得到,点在边上,交于点;下列结论:①;②平分;③,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
10.如图,在中,,将绕点A逆时针旋转得到,连接,则下列结论:①,②,③,④,其中正确的有( )
A.①②③ B.①③④ C.①②④ D.②③④
11.如图,绕直角顶点顺时针旋转,得到,连接,若,则( )
A. B. C. D.
12.如图,在中,,将绕点A顺时针旋转旋转后的对应点分别是和,连接,则的度数是( )
A. B. C. D.
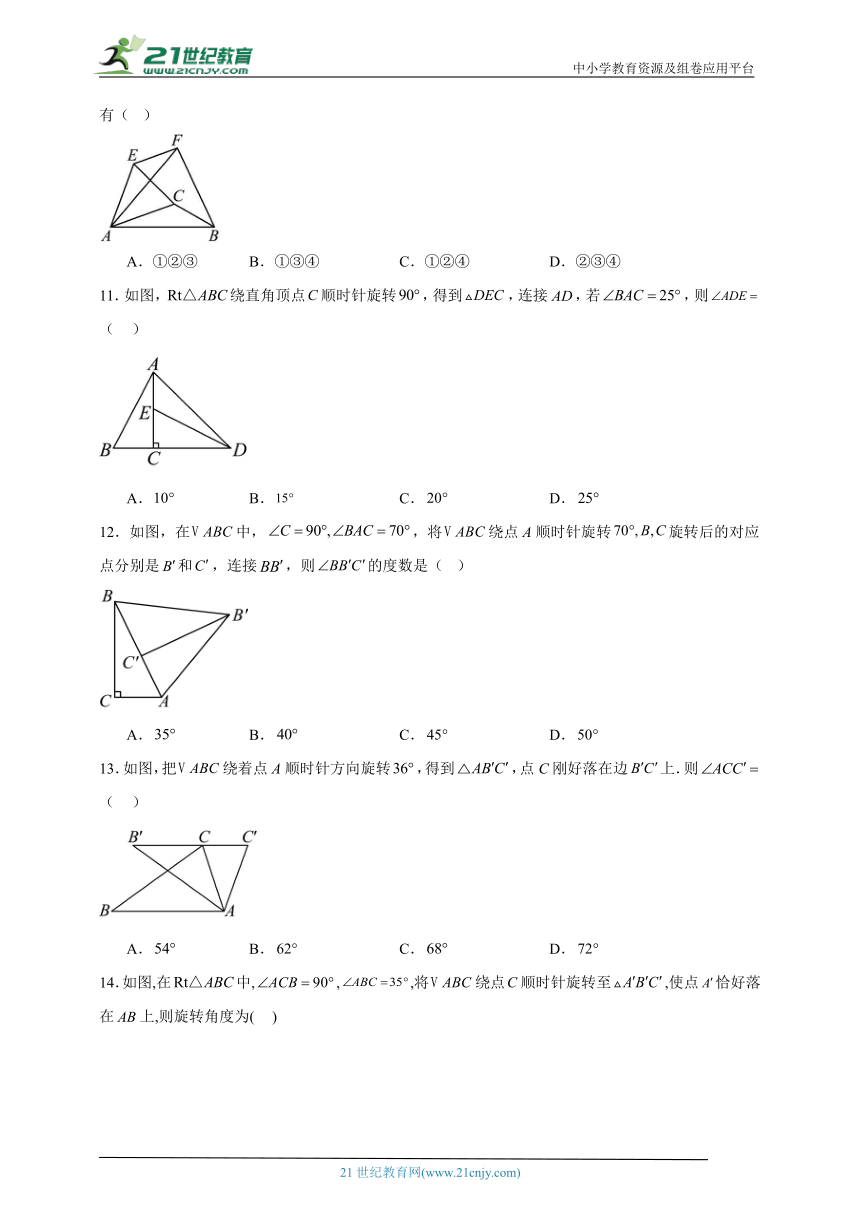
13.如图,把绕着点A顺时针方向旋转,得到,点C刚好落在边上.则( )
A. B. C. D.
14.如图,在中,,,将绕点顺时针旋转至,使点恰好落在上,则旋转角度为( )
A. B. C. D.
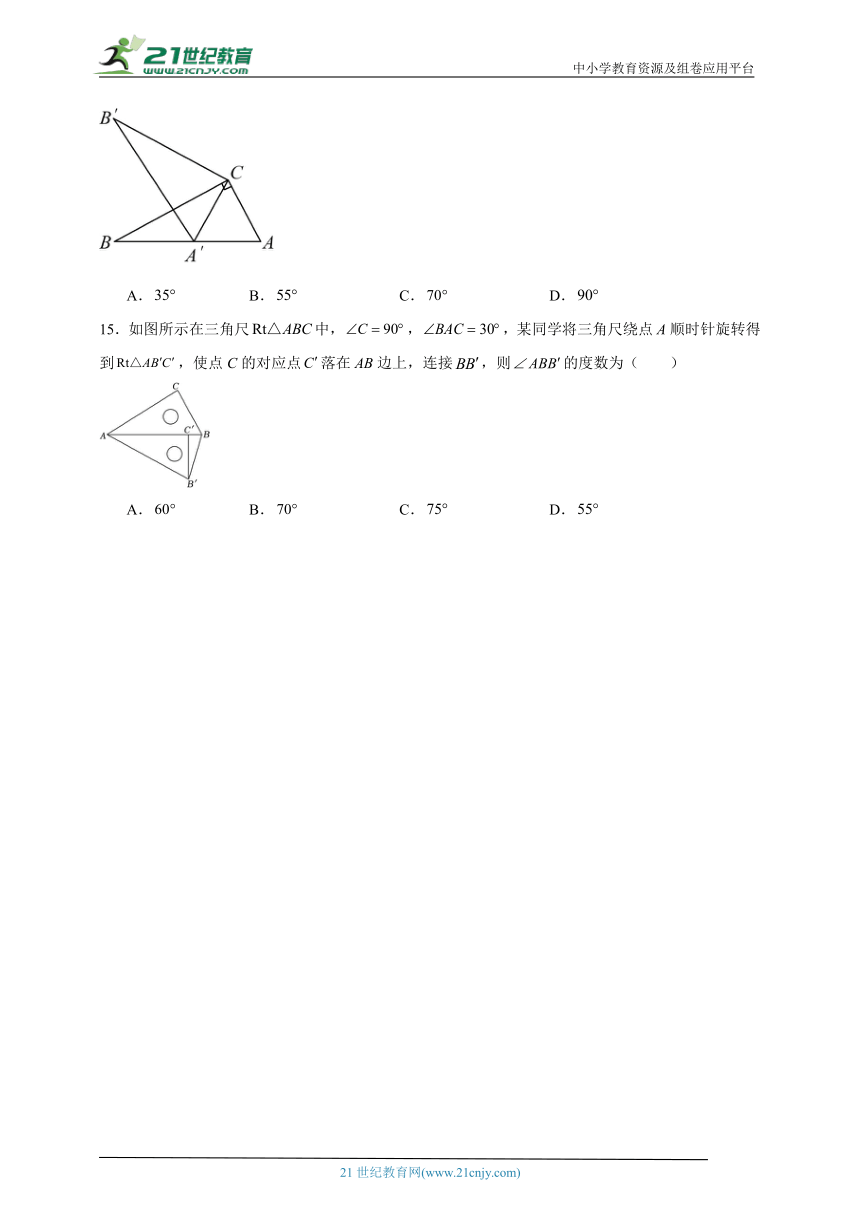
15.如图所示在三角尺中,,,某同学将三角尺绕点A顺时针旋转得到,使点C的对应点落在AB边上,连接,则的度数为( )
A. B. C. D.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B C D C C A D A
题号 11 12 13 14 15
答案 C A D C C
1.A
根据折叠的性质得出,,,的面积的面积,再逐个判断即可.
解:∵,
∴,,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴,即,
∵四边形ABCD是矩形,
∴,,
∴,
∴,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴,,
,
∴,
∴①正确;
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴,
∴.
在和中,
,
∴≌,
∴②正确;
∵,,
∴,,
∴,,
∴,
∴,
∴③正确;
∵,,,
∴,
∴的面积为,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴的面积为,
∴,
∴④正确;
2.D
根据矩形对角线相等且互相平分,可知是等腰三角形,再由,求出进而求出,根据翻折的性质及三角形外角可得,再根据,可判断是等腰直角三角形.根据是等腰直角三角形,且,求出的长,再进一步求出的长.
解:①四边形是矩形,
,,
,
,
,
四边形沿所在的直线翻折,点恰好落在点处,
,
,
是的外角,
,
①错误,不符合题意;
②过点作于点,如图所示:
,
,
由①得,,
,
是等腰直角三角形.故②正确,符合题意;
③在中,设,则由②得,
是等腰直角三角形,
即,解得,
,
过点作,如图所示:
,
,
,
,,
,
四边形是矩形,
,
,故③错误,不符合题意;
正确的结论只有②.即一个正确的结论,
故选:D.
3.B
①连接,首先根据垂直平分,可得;然后根据折叠的性质,可得,据此判断出为等边三角形,即可得出的度数;
②根据题意得到,利用直角三角形性质得到,利用勾股定理算出,即可判断;
③根据折叠的性质,得到,即可证明;
④根据,,推出,即可得到是等边三角形;
⑤连接,点是的中点, 点H是的中点,由折叠的性质可知,点与点关于对称,,即点与点重合时,的值最小, 即,据此求出的最小值即可.
解:连接,
对折矩形纸片,使与重合,折痕为,.
垂直平分,即点是的中点,
,
过点B折叠矩形纸片,使点A落在上的点N,折痕与相交于点Q,
,,,,
,
为等边三角形,
,
即结论①正确;
,,
,
,
,
解得,
即结论②不正确;
由折叠的性质可知,,
;
即结论③正确;
,,
,
,
为等边三角形,
即结论④正确;
连接,
点是的中点, 点H是的中点,
过点B折叠矩形纸片,使点A落在上的点N,折痕与相交于点Q,
即与关于对称,点与点关于对称,
,
点与点重合时,的值最小, 即,
,
,
的最小值是.
即结论⑤正确;
综上所述,正确的结论有个,
4.C
本题考查矩形与折叠,勾股定理,等腰三角形的判定和性质,根据平行线的性质和折叠的性质得出,根据等腰三角形的判定得出;根据折叠和平行线的性质得出,根据等腰三角形的判定得出,证明,设,在中,利用勾股定理求出的值,最后求出结果即可.
解:∵矩形纸片沿所在的直线折叠,
∴,,
∵四边形是矩形,
∴,
∴,
∴,
∴;
由四边形折叠得到四边形,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
即;
设,则:,
在中,由勾股定理,得:,
∴,
∵,
∴,
故选:C.
5.D
连接相交于于点,根据折叠的性质可得,进而得出四边形是平行四边形,设,则,,在中,利用勾股定理列出方程,求得,进而可得.
解:连接相交于于点,
将矩形沿折叠,点恰好落在边上点处,
,,,
,
又将沿折叠,点恰好落在上的点处,,
,,,,
,
,
,
,
,
又四边形是矩形,,
,
四边形是平行四边形,
,
设,则,,
,,
,
,,
在中,,
即,
化简方程解得,,
,
舍去,
,
.
6.C
本题考查了矩形的性质和翻折变换,全等三角形的判定和性质,勾股定理,过点作,交的延长线于点,延长交的延长线于点,则四边形为矩形,由折叠可得,得到,,进而可得,从而判断出点在上运动,又由全等三角形的性质可得,,设 ,则,,由勾股定理得,即得,解方程求出,得到的长度,即可求解,正确作出辅助线是解题的关键.
解:如图,过点作,交的延长线于点,延长交的延长线于点,则四边形为矩形,
∴,,,
由折叠得,,
∴,,
∴,
∵为的平分线,
∴,
在和中,
,
∴,
∴,
∴,
∵点在上,
∴点到的距离等于,即点在上运动,
∴点与点重合时,点与点重合,
当点与点重合时,如图,
∵,
∴,
∵,
∴,
∵ 四边形为矩形,
∴,
设,则,,
∵,
∴,
∴,
解得,
∴,
∴当点从点运动到点时,点运动的路径长为线段的长,等于,
故选:.
7.C
本题考查了矩形的性质,折叠的性质,勾股定理,等腰三角形的性质,三角形内角和定理,连接,与相交于点,由折叠的性质得,根据勾股定理求出,再根据三角形的面积公式求出,得到,再利用等腰三角形的性质和三角形内角和定理得出,根据勾股定理求出的长度,最后根据计算即可求解,正确作出辅助线是解题的关键.
解:连接,与相交于点,
由折叠可知,垂直平分,,
∴,,
∵,点为的中点,
∴,
∴,
又∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,,
∵,
∴,
∴,
即,
∴,
∴,
∵点为的中点,
∴,
故选:.
8.A
本题考查了旋转的性质,平行线的判定和性质,三角板中的角度计算,由旋转的性质和平行线的性质与判定依次判断可求解.
解:由三角板可知,,,,,
(1)当平分,则,
,故(1)错误;
(2)若,且在的上方,则,
,故(2)错误;
(3)若时,且在的下方时,则,故(3)错误;
(4)若,且,则,故(4)正确,
故选:A.
9.D
根据旋转的性质得到,推出即可判断②;利用三角形的外角性质即可判断①;再证明,即可判断③.
解:∵将以点A为旋转中心逆时针旋转得到,
∴,
∴,
∴,
∴平分,故②正确;
∵,,
∴,故①正确;
∵,
∴,
∴,故③正确;
10.A
由旋转的性质可知,,,,,,可判断①的正误;,,,可得,可判断②的正误;,可判断③的正误;由,可知不垂直,可判断④的正误.
解:由旋转的性质可知,,,,,,①正确,故符合要求;
∴,,,
∴,②正确,故符合要求;,③正确,故符合要求;
∵,
∴不垂直,④错误,故不符合要求;
综上所述,①②③正确,
故选:A.
11.C
解:∵绕其直角顶点C按顺时针方向旋转后得到,
∴,,
∴是等腰直角三角形,
∴,
∴.
故选C.
12.A
解∵旋转,
∴,,,
∴,,
∴,
故选:A.
13.D
此题主要考查了旋转的性质以及等腰三角形的性质等知识,根据题意得出是解题关键.
解:∵把绕着点A顺时针方向旋转,得到,
∴,,
∴.
故选:D.
14.C
本题考查旋转性质,三角形内角和定理,等腰三角形性质.根据题意可知,即,再代入已知条件即可求得本题答案.
解:∵,,
∴,
∵将绕点顺时针旋转至,即其中一个旋转角为,
∴,
∴是等腰三角形,
∴,
∴,
故选:C.
15.C
解:由旋转得:,,
,
故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
旋转和折叠重点考点单选题 归类练
2025年中考数学一轮复习备考
一、单选题
1.如图,在矩形ABCD中,点E、F分别在边AB、BC上,且,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:
①;②≌;
③;④.
其中正确的结论是( ).
A.①②③④ B.①②③ C.②③④ D.①③④
2.如图,在矩形ABCD中,对角线AC,BD交于点O,,点E在边AD上,,点F在边BC上,将四边形CDEF沿EF所在的直线翻折,点D恰好落在点O处,点C落在点处.下列结论中,正确的有( )
①;②过点O作于点P,是等腰直角三角形;③AB的长为
A.3个 B.2个 C.0个 D.1个
3.如图,四边形是矩形纸片,.对折矩形纸片,使与重合,折痕为;展平后再过点B折叠矩形纸片,使点A落在上的点N,折痕与相交于点Q;再次展平,连接,,延长交于点G.有如下结论:①;②;③;④是等边三角形;⑤点P为线段上一动点,点H是的中点,则的最小值是.其中正确结论有( )
A.5个 B.4个 C.3个 D.2个
4.如图,在矩形中,点M在边上,先将矩形纸片沿所在的直线折叠,使点D落在点处,与交于点N.之后再将矩形纸片折叠,使恰好落在直线上,点A落在点处,点B落在点处,折痕为.若,,则的长为( )
A.6 B.8 C.10 D.12
5.如图,在矩形中,,分别是边,上的点,且,将矩形沿折叠,点恰好落在边上点处,再将沿折叠,点恰好落在上的点处.若,,则的长为( )
A. B. C. D.
6.如图,点E是矩形边上一点,连接,将沿翻折,点落在点处,的角平分线与的延长线交于点,若,,当点从点运动到点时,则点运动的路径长是( )
A. B. C. D.
7.如图,在矩形中,,,点为的中点,将沿折叠,使点落在矩形内点处,连接,则的面积为( )
A. B. C. D.
8.将一副三角板按如图放置,三角板可绕点旋转,点为与的交点,下列结论中正确的个数是( )
(1)若平分,则
(2)若,则
(3)若,则
(4)若,则
A.1个 B.2个 C.3个 D.4个
9.如图,在中,,将以点为中心逆时针旋转得到,点在边上,交于点;下列结论:①;②平分;③,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
10.如图,在中,,将绕点A逆时针旋转得到,连接,则下列结论:①,②,③,④,其中正确的有( )
A.①②③ B.①③④ C.①②④ D.②③④
11.如图,绕直角顶点顺时针旋转,得到,连接,若,则( )
A. B. C. D.
12.如图,在中,,将绕点A顺时针旋转旋转后的对应点分别是和,连接,则的度数是( )
A. B. C. D.
13.如图,把绕着点A顺时针方向旋转,得到,点C刚好落在边上.则( )
A. B. C. D.
14.如图,在中,,,将绕点顺时针旋转至,使点恰好落在上,则旋转角度为( )
A. B. C. D.
15.如图所示在三角尺中,,,某同学将三角尺绕点A顺时针旋转得到,使点C的对应点落在AB边上,连接,则的度数为( )
A. B. C. D.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B C D C C A D A
题号 11 12 13 14 15
答案 C A D C C
1.A
根据折叠的性质得出,,,的面积的面积,再逐个判断即可.
解:∵,
∴,,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴,即,
∵四边形ABCD是矩形,
∴,,
∴,
∴,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴,,
,
∴,
∴①正确;
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴,
∴.
在和中,
,
∴≌,
∴②正确;
∵,,
∴,,
∴,,
∴,
∴,
∴③正确;
∵,,,
∴,
∴的面积为,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴的面积为,
∴,
∴④正确;
2.D
根据矩形对角线相等且互相平分,可知是等腰三角形,再由,求出进而求出,根据翻折的性质及三角形外角可得,再根据,可判断是等腰直角三角形.根据是等腰直角三角形,且,求出的长,再进一步求出的长.
解:①四边形是矩形,
,,
,
,
,
四边形沿所在的直线翻折,点恰好落在点处,
,
,
是的外角,
,
①错误,不符合题意;
②过点作于点,如图所示:
,
,
由①得,,
,
是等腰直角三角形.故②正确,符合题意;
③在中,设,则由②得,
是等腰直角三角形,
即,解得,
,
过点作,如图所示:
,
,
,
,,
,
四边形是矩形,
,
,故③错误,不符合题意;
正确的结论只有②.即一个正确的结论,
故选:D.
3.B
①连接,首先根据垂直平分,可得;然后根据折叠的性质,可得,据此判断出为等边三角形,即可得出的度数;
②根据题意得到,利用直角三角形性质得到,利用勾股定理算出,即可判断;
③根据折叠的性质,得到,即可证明;
④根据,,推出,即可得到是等边三角形;
⑤连接,点是的中点, 点H是的中点,由折叠的性质可知,点与点关于对称,,即点与点重合时,的值最小, 即,据此求出的最小值即可.
解:连接,
对折矩形纸片,使与重合,折痕为,.
垂直平分,即点是的中点,
,
过点B折叠矩形纸片,使点A落在上的点N,折痕与相交于点Q,
,,,,
,
为等边三角形,
,
即结论①正确;
,,
,
,
,
解得,
即结论②不正确;
由折叠的性质可知,,
;
即结论③正确;
,,
,
,
为等边三角形,
即结论④正确;
连接,
点是的中点, 点H是的中点,
过点B折叠矩形纸片,使点A落在上的点N,折痕与相交于点Q,
即与关于对称,点与点关于对称,
,
点与点重合时,的值最小, 即,
,
,
的最小值是.
即结论⑤正确;
综上所述,正确的结论有个,
4.C
本题考查矩形与折叠,勾股定理,等腰三角形的判定和性质,根据平行线的性质和折叠的性质得出,根据等腰三角形的判定得出;根据折叠和平行线的性质得出,根据等腰三角形的判定得出,证明,设,在中,利用勾股定理求出的值,最后求出结果即可.
解:∵矩形纸片沿所在的直线折叠,
∴,,
∵四边形是矩形,
∴,
∴,
∴,
∴;
由四边形折叠得到四边形,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
即;
设,则:,
在中,由勾股定理,得:,
∴,
∵,
∴,
故选:C.
5.D
连接相交于于点,根据折叠的性质可得,进而得出四边形是平行四边形,设,则,,在中,利用勾股定理列出方程,求得,进而可得.
解:连接相交于于点,
将矩形沿折叠,点恰好落在边上点处,
,,,
,
又将沿折叠,点恰好落在上的点处,,
,,,,
,
,
,
,
,
又四边形是矩形,,
,
四边形是平行四边形,
,
设,则,,
,,
,
,,
在中,,
即,
化简方程解得,,
,
舍去,
,
.
6.C
本题考查了矩形的性质和翻折变换,全等三角形的判定和性质,勾股定理,过点作,交的延长线于点,延长交的延长线于点,则四边形为矩形,由折叠可得,得到,,进而可得,从而判断出点在上运动,又由全等三角形的性质可得,,设 ,则,,由勾股定理得,即得,解方程求出,得到的长度,即可求解,正确作出辅助线是解题的关键.
解:如图,过点作,交的延长线于点,延长交的延长线于点,则四边形为矩形,
∴,,,
由折叠得,,
∴,,
∴,
∵为的平分线,
∴,
在和中,
,
∴,
∴,
∴,
∵点在上,
∴点到的距离等于,即点在上运动,
∴点与点重合时,点与点重合,
当点与点重合时,如图,
∵,
∴,
∵,
∴,
∵ 四边形为矩形,
∴,
设,则,,
∵,
∴,
∴,
解得,
∴,
∴当点从点运动到点时,点运动的路径长为线段的长,等于,
故选:.
7.C
本题考查了矩形的性质,折叠的性质,勾股定理,等腰三角形的性质,三角形内角和定理,连接,与相交于点,由折叠的性质得,根据勾股定理求出,再根据三角形的面积公式求出,得到,再利用等腰三角形的性质和三角形内角和定理得出,根据勾股定理求出的长度,最后根据计算即可求解,正确作出辅助线是解题的关键.
解:连接,与相交于点,
由折叠可知,垂直平分,,
∴,,
∵,点为的中点,
∴,
∴,
又∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,,
∵,
∴,
∴,
即,
∴,
∴,
∵点为的中点,
∴,
故选:.
8.A
本题考查了旋转的性质,平行线的判定和性质,三角板中的角度计算,由旋转的性质和平行线的性质与判定依次判断可求解.
解:由三角板可知,,,,,
(1)当平分,则,
,故(1)错误;
(2)若,且在的上方,则,
,故(2)错误;
(3)若时,且在的下方时,则,故(3)错误;
(4)若,且,则,故(4)正确,
故选:A.
9.D
根据旋转的性质得到,推出即可判断②;利用三角形的外角性质即可判断①;再证明,即可判断③.
解:∵将以点A为旋转中心逆时针旋转得到,
∴,
∴,
∴,
∴平分,故②正确;
∵,,
∴,故①正确;
∵,
∴,
∴,故③正确;
10.A
由旋转的性质可知,,,,,,可判断①的正误;,,,可得,可判断②的正误;,可判断③的正误;由,可知不垂直,可判断④的正误.
解:由旋转的性质可知,,,,,,①正确,故符合要求;
∴,,,
∴,②正确,故符合要求;,③正确,故符合要求;
∵,
∴不垂直,④错误,故不符合要求;
综上所述,①②③正确,
故选:A.
11.C
解:∵绕其直角顶点C按顺时针方向旋转后得到,
∴,,
∴是等腰直角三角形,
∴,
∴.
故选C.
12.A
解∵旋转,
∴,,,
∴,,
∴,
故选:A.
13.D
此题主要考查了旋转的性质以及等腰三角形的性质等知识,根据题意得出是解题关键.
解:∵把绕着点A顺时针方向旋转,得到,
∴,,
∴.
故选:D.
14.C
本题考查旋转性质,三角形内角和定理,等腰三角形性质.根据题意可知,即,再代入已知条件即可求得本题答案.
解:∵,,
∴,
∵将绕点顺时针旋转至,即其中一个旋转角为,
∴,
∴是等腰三角形,
∴,
∴,
故选:C.
15.C
解:由旋转得:,,
,
故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
