实际问题与二次函数热点考点 专题练 2025年中考数学一轮复习备考
文档属性
| 名称 | 实际问题与二次函数热点考点 专题练 2025年中考数学一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 16:53:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
实际问题与二次函数热点考点 专题练
2025年中考数学一轮复习备考
一、解答题
1.如图,斜坡上种有若干树木,底部有一喷水管,某时刻从B处喷出的水流恰好落在A处,水流呈抛物线状.建立恰当平面直角坐标系,得到点,点.已知喷水管及所有树木都与垂直,抛物线的解析式为
(1)求该抛物线解析式,并写出其顶点坐标.
(2)若抛物线恰好过小树的树顶N,点M在斜坡上,且点A到M,N两点距离相等,求M点坐标.
(3)若,为两棵等高小树(在左侧,小树粗细忽略不计,点M,D均在斜坡上且与点C不重合),抛物线恰好经过E,N两点.
①当时,求长;
②直接写出M横坐标m的取值范围.
2.如图,某条河流上桥的钢拱圈截面形状类似于抛物线,钢拱圈与桥面两接触点M,N之间的距离为20米,A,B两点为钢拱圈的钢丝固定点且距离桥面高度均为30米,C,D为桥面钢丝的固定点,C,D两点相距90米且,已知.
(1)以M为坐标原点,所在直线为x轴,垂直于的直线为y轴构建平面直角坐标系,求抛物线的函数表达式;
(2)现要在钢拱圈上挂一幅公益宣传海报,海报为正方形,海报顶边的两个顶点恰好在钢拱圈上的A,B两点,求海报底边与桥面的距离.
3.如图1所示,公园有一斜坡草坪可以看成射线OA,其倾斜角为,该斜坡上有一棵小树(垂直于水平面),树高,现给该草坪洒水,已知小树的底端点与喷水点的距,建立如图所示的平面直角坐标系,在喷水过程中,水运行的路线是抛物线水路到达的最大高度是米,且恰好经过小树的顶端点,最远处落在草坪的处.
(1)求:抛物线的关系式;
(2)如图2,现决定在山上种另一棵树(垂直于水平面),树的最高点不能超过喷水路线,为了加固树,沿斜坡垂直的方向加一根支架,求出的最大值.
4.如图,一高尔夫球从山坡下的点处打出一球,球向山坡上的球洞点处飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球达到最大高度时,球移动的水平距离为.已知山坡与水平方向的夹角为30°,、两点间的距离为.
(1)建立适当的直角坐标系,求这个球的飞行路线所在抛物线的函数表达式.
(2)这一杆能否把高尔夫球从点处直接打入点处球洞?
5.如图1是一个高脚杯的截面图,杯体呈抛物线形(杯体厚度不计),杯底,点O是的中点,,杯子的高度(即,之间的距离)为,所在直线为x轴,所在直线为y轴建立平面直角坐标系(1个单位长度表示).
(1)求杯体所在抛物线的解析式;
(2)将杯子向右平移,并倒满饮料,杯体与y轴交于点E(图2),过D点放一根吸管,吸管底部碰触到杯壁后不再移动,发现剩余饮料的液面低于点E,设吸管所在直线的解析式为,求k的取值范围;
(3)如图3,将放在水平桌面上的装有饮料的高脚杯绕点B顺时针旋转,液面恰好到达点D处(),请求出此时杯子内液体的最大深度.
6.某公园要在小广场上建造一个喷泉景观.在小广场中央处垂直于地面安装一个高为1.25米的花形柱子,安置于柱子顶端A处的喷水向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过的任一平面上抛物线路径如图1所示.为使水流形状较为美观,设计成水流在距的水平距离为1米时到达最大高度,此时离地面2.25米.
(1)以点为原点建立如图2所示的平面直角坐标系,水流到水平距离为米,水流喷出的高度为米,求出在第一象限内的抛物线解析式(不要求写出自变量的取值范围);
(2)张师傅正在喷泉景观内维修设备期间,喷水管意外喷水,但是身高1.76米的张师傅却没有被水淋到,此时他离花形柱子的距离为米,则的取值范围是______________;
(3)在平面内,把一个图形上的任意一点与另一个图形上任意一点之间的距离的最小值称为这两个图形的距离.为了美观,在离花形柱子4米处的地面处安装射灯,射灯射出的光线与地面成角,如图3所示,光线交汇点在花形柱子的正上方,其中光线所在的直线解析式为,求光线与抛物线水流之间的距离.
7.【项目式学习】
【项目主题】自动旋转式洒水喷头灌溉蔬菜
【项目背景】寻找生活中的数学,九(1)班分四个小组,开展数学项目式实践活动,获取所有数据共享,对蔬菜喷水管建立数学模型.菜地装有1个自动旋转式洒水喷头灌溉蔬菜,如图1所示,观察喷头可顺、逆时针往返喷洒.
【项目素材】
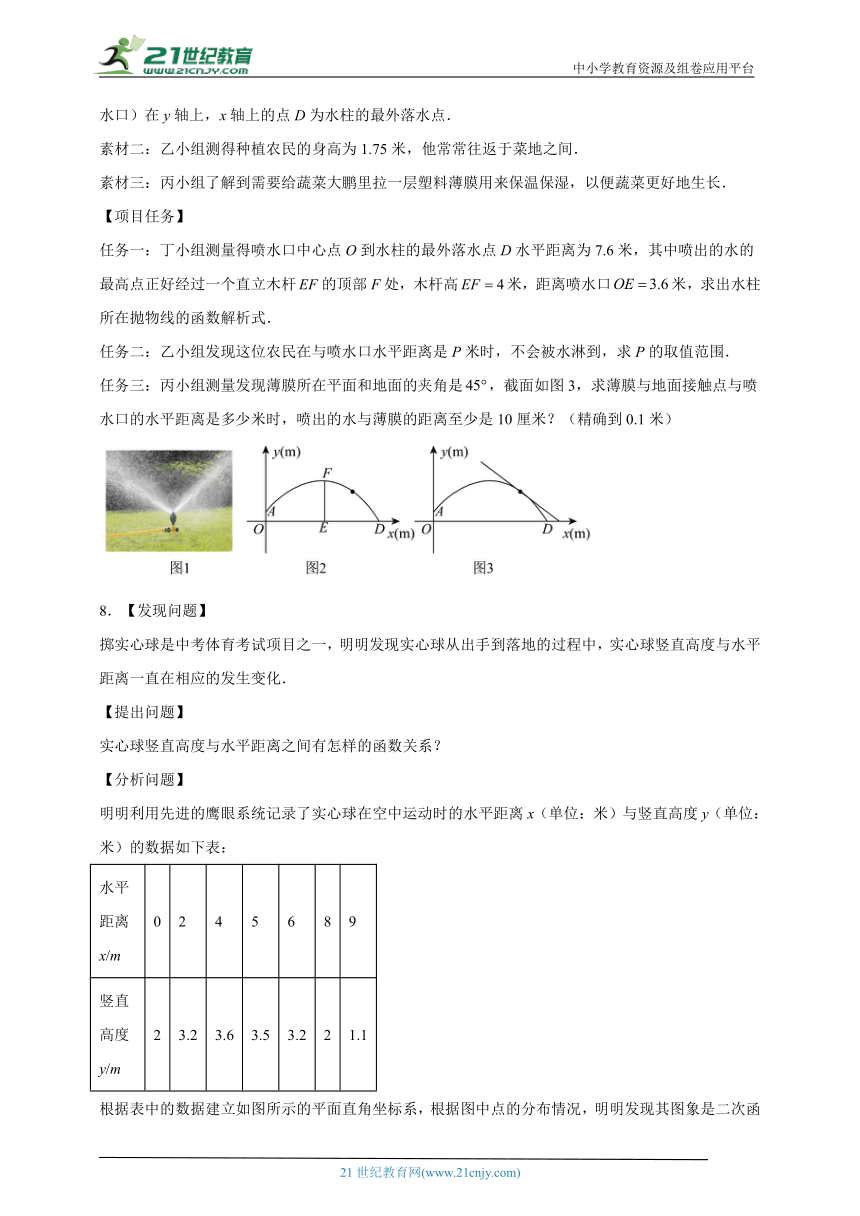
素材一:甲小组在图2中建立合适的直角坐标系,喷水口中心O有一喷水管,从A点向外喷水,喷出的水柱最外层的形状为抛物线,以水平方向为x轴,点O为原点建立平面直角坐标系,点A(喷水口)在y轴上,x轴上的点D为水柱的最外落水点.
素材二:乙小组测得种植农民的身高为1.75米,他常常往返于菜地之间.
素材三:丙小组了解到需要给蔬菜大鹏里拉一层塑料薄膜用来保温保湿,以便蔬菜更好地生长.
【项目任务】
任务一:丁小组测量得喷水口中心点O到水柱的最外落水点D水平距离为7.6米,其中喷出的水的最高点正好经过一个直立木杆的顶部F处,木杆高米,距离喷水口米,求出水柱所在抛物线的函数解析式.
任务二:乙小组发现这位农民在与喷水口水平距离是P米时,不会被水淋到,求P的取值范围.
任务三:丙小组测量发现薄膜所在平面和地面的夹角是,截面如图3,求薄膜与地面接触点与喷水口的水平距离是多少米时,喷出的水与薄膜的距离至少是10厘米?(精确到0.1米)
8.【发现问题】
掷实心球是中考体育考试项目之一,明明发现实心球从出手到落地的过程中,实心球竖直高度与水平距离一直在相应的发生变化.
【提出问题】
实心球竖直高度与水平距离之间有怎样的函数关系?
【分析问题】
明明利用先进的鹰眼系统记录了实心球在空中运动时的水平距离x(单位:米)与竖直高度y(单位:米)的数据如下表:
水平距离x/m 0 2 4 5 6 8 9
竖直高度y/m 2 3.2 3.6 3.5 3.2 2 1.1
根据表中的数据建立如图所示的平面直角坐标系,根据图中点的分布情况,明明发现其图象是二次函数的一部分.
【解决问题】
(1)在明明投掷过程中,出手时实心球的竖直高度是______米,实心球在空中的最大高度是______米;
(2)求满足条件的抛物线的解析式;
(3)根据中考体育考试评分标准(男生版),在投掷过程中,实心球从起点到落地点的水平距离大于或等于9.7米时,即可得满分10分,明明在此次考试中是否得到满分,请说明理由.
(4)若抛物线上有点,点,点C是第一象限内抛物线上的一个动点,使得,请求出C点坐标.
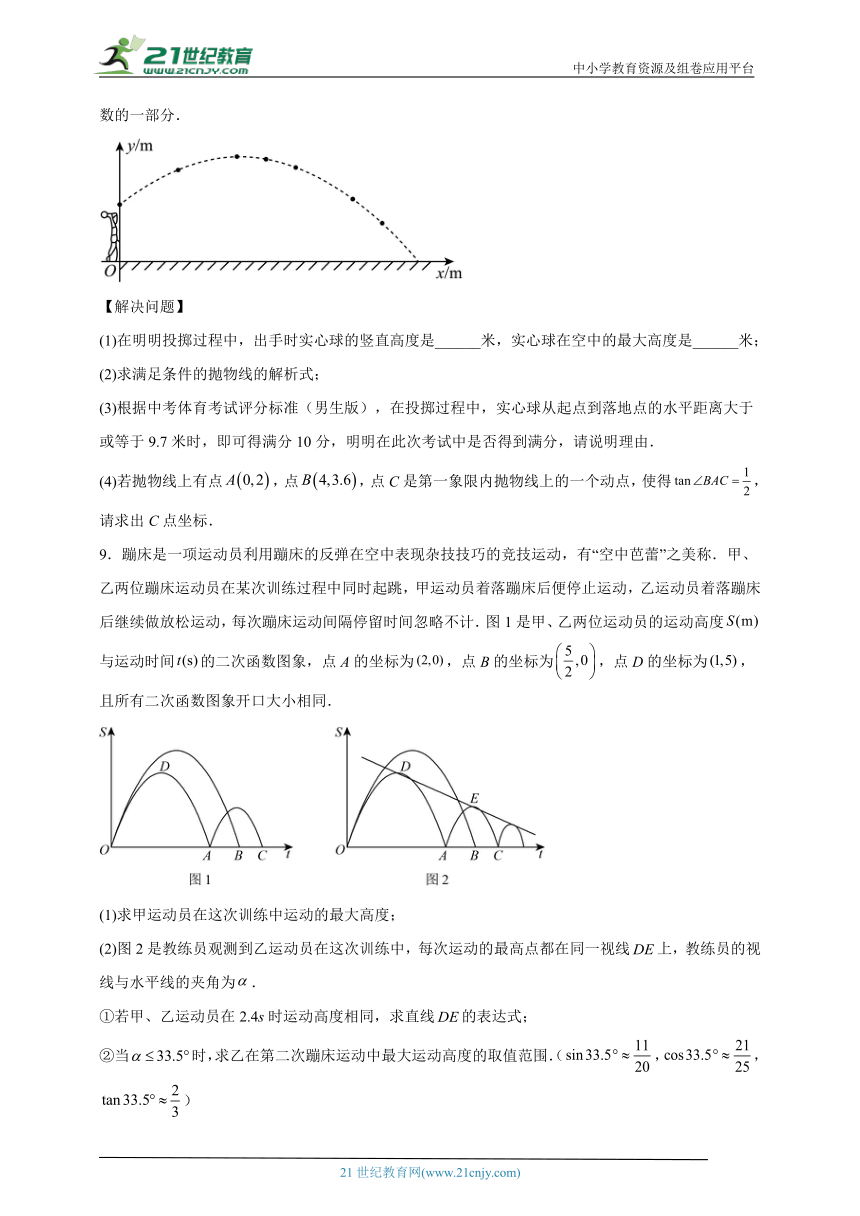
9.蹦床是一项运动员利用蹦床的反弹在空中表现杂技技巧的竞技运动,有“空中芭蕾”之美称.甲、乙两位蹦床运动员在某次训练过程中同时起跳,甲运动员着落蹦床后便停止运动,乙运动员着落蹦床后继续做放松运动,每次蹦床运动间隔停留时间忽略不计.图1是甲、乙两位运动员的运动高度与运动时间的二次函数图象,点A的坐标为,点B的坐标为,点D的坐标为,且所有二次函数图象开口大小相同.
(1)求甲运动员在这次训练中运动的最大高度;
(2)图2是教练员观测到乙运动员在这次训练中,每次运动的最高点都在同一视线上,教练员的视线与水平线的夹角为.
①若甲、乙运动员在2.4s时运动高度相同,求直线的表达式;
②当时,求乙在第二次蹦床运动中最大运动高度的取值范围.(,,)
10.如图1,我校“世界广场”内有一圆形喷泉水池,水池正中央有一凸起的圆柱,圆柱上底面刻有世界地图,俯看喷泉水池呈圆环形.水池内圆柱周围均匀安装有12个喷头(用、、…来表示),喷头口与水面持平,每个喷头喷出的水柱为形状相同的抛物线.每天清晨开放喷泉,给校园增添了许多活力.如图2,实测水池(外圆)的半径米,圆柱底面半径米;圆柱露出水面的高度米,每个喷头口到圆柱的距离均为2米,如米.以为坐标原点,所在直线为轴,所在直线为轴,建立平面直角坐标系.
(1)当由喷头喷出的水柱经过高度为2米且离点的水平距离为1米的位置时,水柱刚好落在圆柱的边缘点处,求此时抛物线的表达式.
(2)由与喷头相对的喷出的水柱形成的抛物线可以看成是问题(1)中的抛物线关于轴对称后向右平移8个单位得到,直接写出由喷出的水柱形成的抛物线的表达式________.
(3)为形成白川归海的场面,物业师傅调整每个喷头的出水压力和水量,使每一个喷泉水柱达到相同高度后能汇聚一点,测得此时由喷头喷出的水柱最高为米时与的水平距离为4米,直接写出汇聚点的坐标________.
(4)如图3,在(1)的条件下,为烘托气氛,物业师傅在对应喷头口的水池外的地面上均匀安装12个彩色射灯,射灯与喷头相对应(如:在喷头,所在直线上的点、处分别安装与喷头等距离的射灯).为呈现更好的光影效果,要求射灯所在直线与水平面成夹角,即,且水柱上的点到相应射灯所在直线的最小距离为5厘米(不计射灯高度,水柱上的点视为抛物线上的点),求与喷头对应的射灯离水池边缘的距离.
参考答案
1.(1),
(2)
(3)①;②
1)根据在抛物线上建立方程组求解并将解析式整理成的形式即可得解;
(2)先求出直线的解解式,进而设,根据题意得到点在中垂线上,进而由中垂线性质(若为中垂线,则且与交点为中点)解得,得到,根据点在抛物线上即可建立方程求解;
(3)①取,表示任意位置的小树高,令解得横坐标,即可求解;
②设,根据题意得到直线与抛物线在区间上有两交点,为靠左一点的横坐标,注意到,即可结合一元二次方程求根公式通过计算求解;
(1)解:点,点在抛物线上,
∴,
解得:,
∴抛物线方程为,
∴抛物线的顶点坐标为;
(2)解:∵点,点在轴上,
∴,
∵,,
∴设直线的解析式为,即,解得:,
故直线的解析式为,
∵点在直线上,
设,,
∵轴,
∴点在中垂线上,故,
解得:,
∴,
∵点在抛物线上,
∴,整理得:,
解得:(舍)或,此时,
∴.
(3)解:①令,
则表示小树高,
∵,即,
∴,整理得,
解得:,
∵在左侧,故,,
∴.
②设,则在上有两解,且为其中较小解,
即直线与抛物线在上有两交点,
当时,,
令,得或(舍去),
∴,
又,
对称轴为,
为直线与抛物线两交点中靠左一点的横坐标,故,
综上,;
2.(1);
(2)20米.
(1)解:如图,建立平面直角坐标系,过作于,
则,,,,
∴,
∴,,
∵,
∴米,
∴,
∴,
设抛物线的解析式为,则有:
,
解得,
∴抛物线的函数表达式为;
(2)当时,,
解得:,,
∴,
∵海报为正方形,海报顶边的两个顶点恰好在钢拱圈上的A,B两点,
∴海报底边与桥面的距离为.
3.(1)
(2)
(1)如图,延长交轴于点,则,
,
,,
,
,
,
∵水路到达的最大高度是米,且恰好经过小树的顶端点,则点为抛物线的顶点,
∴设抛物线解析式为
将代入得
解得:
∴抛物线解析式为
(2)由(1)知, 设直线的解析式为则 ,
解得:,
,
如图,设 ,则,
,
,
,
∵轴,
,
,
,
,
∴当 时,取得最大值 ,
答:的最大值为
4.(1)坐标系见解析,y= x2+x
(2)不能
(1)建立平面直角坐标系如图,
∵顶点B的坐标是(9,12),
∴设抛物线的解析式为y=a(x-9)2+12,
∵点O的坐标是(0,0)
∴把点O的坐标代入得:
0=a(0-9)2+12,
解得a= ,
∴抛物线的解析式为y= (x-9)2+12
即y= x2+x;
(2)在Rt△AOC中,
∵∠AOC=30°,OA=8,
∴AC=OA sin30°=8×=4,
OC=OA cos30°=8×=12.
∴点A的坐标为(12,4),
∵当x=12时,y=,
∴这一杆不能把高尔夫球从O点直接打入球洞A点.
5.(1)
(2)
(3)
(1)解:∵,杯子的高度(即,之间的距离)为.
∴,,
设抛物线的解析式为,
∴,
解得,
∴抛物线的解析式为.
(2)解:∵抛物线的解析式为,
∴平移后的解析式为.
∴抛物线的对称轴为直线,
当时,,
∴,
∴的对称点为,
∵点D平移前坐标为,
∴平移后,
设直线的解析式为,
∴,
解得;
∴;
设直线的解析式为,
∴,
解得;
∴,
根据题意,喝过一次饮料后,发现剩余饮料的液面低于点,
∴.
(3)解:根据题意,以的中点O为原点,所在直线为x轴,所在直线为y轴建立平面直角坐标系;,
设与轴的交点为M,直线与轴的交点为S,
∵,杯子的高度(即,之间的距离)为.
∴,,
∵水平桌面上的装有饮料的高脚杯绕点顺时针旋转,
∴,
∵,
∴,
∴,
∴,
∴.
∵抛物线的解析式为,
设点N是抛物线上的一点,且,;
过点N作轴,交于点G,
∵水平桌面上的装有饮料的高脚杯绕点顺时针旋转,
∴,
∵,
∴,
过点G作轴于点E,
∵轴,
∴,,
∴,
∴,
∴,
∴
,
∵,,
∴时,取得最大值,且最大值为,
过点N作于点H,
则,
故的最大值为,
故液体的最大深度为.
6.(1)
(2)
(3)
(1)解:由题意得,在第一象限内的抛物线顶点的坐标,故设抛物线解析式为,
将代入得,
解得,,
在第一象限内的抛物线解析式为;
(2)解:当时,,
解得:,,
的取值范围是;
故答案为:.
(3)解:∵直线的解析式为:,
∴把代入得:,
把代入得:,解得:,
∴,,
∴,,
设平行于直线且与抛物线只有一个交点的直线的解析式为,
联立,即,
整理得:,
令,
解得,
∴直线的解析式为,
如图,设直线与轴的交点为,
把代入得:,
解得:,
则,
∴,
∵,
∴直线到直线的距离为,
根据题意得:光线与抛物线水流之间的距离为光线与抛物线水流之间的最小垂直距离,即直线到直线的距离,
∴光线与抛物线水流之间的距离为.
7.任务一:
任务二:
任务三:薄膜与地面接触点与喷水口的水平距离为8.7米
解:任务一:根据题意得最高点,
设水柱所在抛物线的函数解析式为:.
由题意得:抛物线经过点D的坐标为.
∴,解得a,
∴水柱所在抛物线的函数解析式为:;
任务二:当时,.
解得:.
∴.
任务三:
薄膜所在平面可看成是一条直线.
∵薄膜所在平面和地面的夹角是,
∴薄膜所在平面的直线解析式为:.
当薄膜所在直线与水柱所在抛物线相切时,
,
∴.
∵只有一个交点,
∴,解得.
∴.
∴直线与x轴的交点为.
过点于点M,且,过点F作,交x轴于点.
∴.
由题意得:,
∴(米).
∴(米)
答:薄膜与地面接触点与喷水口的水平距离为8.7米.
8.(1)2,3.6
(2)
(3)明明在此次考试中能得到满分,见解析
(4)点C的坐标为
长线于点F,证明出,得到,设,表示出,,,,然后代入求出,然后求出,所在直线表达式为,然后和抛物线联立求解即可.
(1)解:由题意可知出手时实心球的竖直高度即为时y的值,
通过图表可得当时,,
得在明明投掷过程中,出手时实心球的竖直高度是2米,
由当时,;当时,,
可得对称轴为直线,
则当时,实心球在空中取得最大高度,
通过图表可得当时,,
得实心球在空中的最大高度是3.6米,
故答案为:2,3.6;
(2)解:设抛物线的解析式为,
由(1)得抛物线的顶点坐标为,
则,
得抛物线的解析式为,
把代入,
得,
解得,
∴抛物线的解析式为;
(3)解:明明在此次考试中能得到满分,理由如下:
把代入,
得,
解得或(不符合题意,舍去),
∵,
∴明明在此次考试中能得到满分.
(4)如图所示,
过点B作,过点E作轴交y轴于点D,过点B作交延长线于点F,
∵
∴
∵
∴
∵
∴
∴
∵
∴
∴
设
∵,点
∴,,,
∴
解得
∴
设,所在直线表达式为
∴
∴解得
∴,所在直线表达式为
∴联立和抛物线得,
整理得,
解得(舍去)或
∴将代入
∴点C的坐标为.
9.(1)米
(2)①;②大于或等于,小于
(1)解:乙运动员的第一次的运动高度与运动时间的二次函数图象经过点 ,点D ,点,设其解析式为:,
∴,解得:,即乙运动员的第一次的运动高度与运动时间的二次函数解析式为:,
因为所有二次函数图象开口大小相同.设,把点B 代入得:
,解得:
∴,即,故
甲运动员在这次训练中运动的最大高度是米,时间是秒.
(2)当秒时,,
即乙二次起跳中,当秒时,其高度,设乙二次起跳中的解析式为,将点A 和代入得:
,解得:,即,
∵,
∴点,
∴设直线DE解析式为,
得,解得:,
∴设直线解析式为,
②延长交x轴于,过点D作轴,
点D的坐标为,
∴,,
当时,,
∴,点K的坐标为,
∴直线,
设乙二次起跳中的解析式为,把点A 代入得:,
∴,
所以,
当时,,,
当时, ,
∴,
∴,整理得:,
∴(不合题意舍去),,
当,,
∵,
故,随增大而增大;
故乙在第二次蹦床运动中最大运动高度的取值范围大于或等于,小于.
10.(1)
(2)
(3)
(4)米
(1)解:设此时抛物线的表达式为,
根据题意,抛物线过点和点,
则,
解得:,
∴此时抛物线的表达式为;
(2)解:∵,
∴抛物线图象的对称轴为,
∵直线关于轴对称的直线为,,
抛物线关于轴对称的抛物线图象的对称轴为,
即抛物线关于轴对称的抛物线解析式为:,
再将抛物线:向右平移8个单位得到,
∴喷出的水柱形成的抛物线的表达式:;
(3)解:如图,
根据题意喷出的水柱形成的抛物线图象的对称轴为,与x轴的一个交点,
∴顶点坐标为,
∵,
∴与x轴的一个交点坐标为,
设喷出的水柱形成的抛物线表达式为:,
将点代入,得,
解得:,
∴喷出的水柱形成的抛物线表达式为:,
同理,喷出的水柱形成的抛物线的图象过点,
则喷出的水柱形成的抛物线的表达式为:,
令,
解得:,则,
∴汇聚点的坐标为;
(4)解:设直线的方程为,与直线平行的直线的方程为,
∴联立,得,
∴,
由题意知:直线与抛物线相切时,水柱上的点到相应射灯所在直线的距离最小,
故,即,
∴,
如图,设直线与抛物线切于点K,过点K作的平行线,过点作轴交于点F,
则,
又厘米,
∴在中,厘米,
∴直线可以看成是将直线向左平移个单位得到,
即直线,
令,则,
∴,
∵,
∴米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
实际问题与二次函数热点考点 专题练
2025年中考数学一轮复习备考
一、解答题
1.如图,斜坡上种有若干树木,底部有一喷水管,某时刻从B处喷出的水流恰好落在A处,水流呈抛物线状.建立恰当平面直角坐标系,得到点,点.已知喷水管及所有树木都与垂直,抛物线的解析式为
(1)求该抛物线解析式,并写出其顶点坐标.
(2)若抛物线恰好过小树的树顶N,点M在斜坡上,且点A到M,N两点距离相等,求M点坐标.
(3)若,为两棵等高小树(在左侧,小树粗细忽略不计,点M,D均在斜坡上且与点C不重合),抛物线恰好经过E,N两点.
①当时,求长;
②直接写出M横坐标m的取值范围.
2.如图,某条河流上桥的钢拱圈截面形状类似于抛物线,钢拱圈与桥面两接触点M,N之间的距离为20米,A,B两点为钢拱圈的钢丝固定点且距离桥面高度均为30米,C,D为桥面钢丝的固定点,C,D两点相距90米且,已知.
(1)以M为坐标原点,所在直线为x轴,垂直于的直线为y轴构建平面直角坐标系,求抛物线的函数表达式;
(2)现要在钢拱圈上挂一幅公益宣传海报,海报为正方形,海报顶边的两个顶点恰好在钢拱圈上的A,B两点,求海报底边与桥面的距离.
3.如图1所示,公园有一斜坡草坪可以看成射线OA,其倾斜角为,该斜坡上有一棵小树(垂直于水平面),树高,现给该草坪洒水,已知小树的底端点与喷水点的距,建立如图所示的平面直角坐标系,在喷水过程中,水运行的路线是抛物线水路到达的最大高度是米,且恰好经过小树的顶端点,最远处落在草坪的处.
(1)求:抛物线的关系式;
(2)如图2,现决定在山上种另一棵树(垂直于水平面),树的最高点不能超过喷水路线,为了加固树,沿斜坡垂直的方向加一根支架,求出的最大值.
4.如图,一高尔夫球从山坡下的点处打出一球,球向山坡上的球洞点处飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球达到最大高度时,球移动的水平距离为.已知山坡与水平方向的夹角为30°,、两点间的距离为.
(1)建立适当的直角坐标系,求这个球的飞行路线所在抛物线的函数表达式.
(2)这一杆能否把高尔夫球从点处直接打入点处球洞?
5.如图1是一个高脚杯的截面图,杯体呈抛物线形(杯体厚度不计),杯底,点O是的中点,,杯子的高度(即,之间的距离)为,所在直线为x轴,所在直线为y轴建立平面直角坐标系(1个单位长度表示).
(1)求杯体所在抛物线的解析式;
(2)将杯子向右平移,并倒满饮料,杯体与y轴交于点E(图2),过D点放一根吸管,吸管底部碰触到杯壁后不再移动,发现剩余饮料的液面低于点E,设吸管所在直线的解析式为,求k的取值范围;
(3)如图3,将放在水平桌面上的装有饮料的高脚杯绕点B顺时针旋转,液面恰好到达点D处(),请求出此时杯子内液体的最大深度.
6.某公园要在小广场上建造一个喷泉景观.在小广场中央处垂直于地面安装一个高为1.25米的花形柱子,安置于柱子顶端A处的喷水向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过的任一平面上抛物线路径如图1所示.为使水流形状较为美观,设计成水流在距的水平距离为1米时到达最大高度,此时离地面2.25米.
(1)以点为原点建立如图2所示的平面直角坐标系,水流到水平距离为米,水流喷出的高度为米,求出在第一象限内的抛物线解析式(不要求写出自变量的取值范围);
(2)张师傅正在喷泉景观内维修设备期间,喷水管意外喷水,但是身高1.76米的张师傅却没有被水淋到,此时他离花形柱子的距离为米,则的取值范围是______________;
(3)在平面内,把一个图形上的任意一点与另一个图形上任意一点之间的距离的最小值称为这两个图形的距离.为了美观,在离花形柱子4米处的地面处安装射灯,射灯射出的光线与地面成角,如图3所示,光线交汇点在花形柱子的正上方,其中光线所在的直线解析式为,求光线与抛物线水流之间的距离.
7.【项目式学习】
【项目主题】自动旋转式洒水喷头灌溉蔬菜
【项目背景】寻找生活中的数学,九(1)班分四个小组,开展数学项目式实践活动,获取所有数据共享,对蔬菜喷水管建立数学模型.菜地装有1个自动旋转式洒水喷头灌溉蔬菜,如图1所示,观察喷头可顺、逆时针往返喷洒.
【项目素材】
素材一:甲小组在图2中建立合适的直角坐标系,喷水口中心O有一喷水管,从A点向外喷水,喷出的水柱最外层的形状为抛物线,以水平方向为x轴,点O为原点建立平面直角坐标系,点A(喷水口)在y轴上,x轴上的点D为水柱的最外落水点.
素材二:乙小组测得种植农民的身高为1.75米,他常常往返于菜地之间.
素材三:丙小组了解到需要给蔬菜大鹏里拉一层塑料薄膜用来保温保湿,以便蔬菜更好地生长.
【项目任务】
任务一:丁小组测量得喷水口中心点O到水柱的最外落水点D水平距离为7.6米,其中喷出的水的最高点正好经过一个直立木杆的顶部F处,木杆高米,距离喷水口米,求出水柱所在抛物线的函数解析式.
任务二:乙小组发现这位农民在与喷水口水平距离是P米时,不会被水淋到,求P的取值范围.
任务三:丙小组测量发现薄膜所在平面和地面的夹角是,截面如图3,求薄膜与地面接触点与喷水口的水平距离是多少米时,喷出的水与薄膜的距离至少是10厘米?(精确到0.1米)
8.【发现问题】
掷实心球是中考体育考试项目之一,明明发现实心球从出手到落地的过程中,实心球竖直高度与水平距离一直在相应的发生变化.
【提出问题】
实心球竖直高度与水平距离之间有怎样的函数关系?
【分析问题】
明明利用先进的鹰眼系统记录了实心球在空中运动时的水平距离x(单位:米)与竖直高度y(单位:米)的数据如下表:
水平距离x/m 0 2 4 5 6 8 9
竖直高度y/m 2 3.2 3.6 3.5 3.2 2 1.1
根据表中的数据建立如图所示的平面直角坐标系,根据图中点的分布情况,明明发现其图象是二次函数的一部分.
【解决问题】
(1)在明明投掷过程中,出手时实心球的竖直高度是______米,实心球在空中的最大高度是______米;
(2)求满足条件的抛物线的解析式;
(3)根据中考体育考试评分标准(男生版),在投掷过程中,实心球从起点到落地点的水平距离大于或等于9.7米时,即可得满分10分,明明在此次考试中是否得到满分,请说明理由.
(4)若抛物线上有点,点,点C是第一象限内抛物线上的一个动点,使得,请求出C点坐标.
9.蹦床是一项运动员利用蹦床的反弹在空中表现杂技技巧的竞技运动,有“空中芭蕾”之美称.甲、乙两位蹦床运动员在某次训练过程中同时起跳,甲运动员着落蹦床后便停止运动,乙运动员着落蹦床后继续做放松运动,每次蹦床运动间隔停留时间忽略不计.图1是甲、乙两位运动员的运动高度与运动时间的二次函数图象,点A的坐标为,点B的坐标为,点D的坐标为,且所有二次函数图象开口大小相同.
(1)求甲运动员在这次训练中运动的最大高度;
(2)图2是教练员观测到乙运动员在这次训练中,每次运动的最高点都在同一视线上,教练员的视线与水平线的夹角为.
①若甲、乙运动员在2.4s时运动高度相同,求直线的表达式;
②当时,求乙在第二次蹦床运动中最大运动高度的取值范围.(,,)
10.如图1,我校“世界广场”内有一圆形喷泉水池,水池正中央有一凸起的圆柱,圆柱上底面刻有世界地图,俯看喷泉水池呈圆环形.水池内圆柱周围均匀安装有12个喷头(用、、…来表示),喷头口与水面持平,每个喷头喷出的水柱为形状相同的抛物线.每天清晨开放喷泉,给校园增添了许多活力.如图2,实测水池(外圆)的半径米,圆柱底面半径米;圆柱露出水面的高度米,每个喷头口到圆柱的距离均为2米,如米.以为坐标原点,所在直线为轴,所在直线为轴,建立平面直角坐标系.
(1)当由喷头喷出的水柱经过高度为2米且离点的水平距离为1米的位置时,水柱刚好落在圆柱的边缘点处,求此时抛物线的表达式.
(2)由与喷头相对的喷出的水柱形成的抛物线可以看成是问题(1)中的抛物线关于轴对称后向右平移8个单位得到,直接写出由喷出的水柱形成的抛物线的表达式________.
(3)为形成白川归海的场面,物业师傅调整每个喷头的出水压力和水量,使每一个喷泉水柱达到相同高度后能汇聚一点,测得此时由喷头喷出的水柱最高为米时与的水平距离为4米,直接写出汇聚点的坐标________.
(4)如图3,在(1)的条件下,为烘托气氛,物业师傅在对应喷头口的水池外的地面上均匀安装12个彩色射灯,射灯与喷头相对应(如:在喷头,所在直线上的点、处分别安装与喷头等距离的射灯).为呈现更好的光影效果,要求射灯所在直线与水平面成夹角,即,且水柱上的点到相应射灯所在直线的最小距离为5厘米(不计射灯高度,水柱上的点视为抛物线上的点),求与喷头对应的射灯离水池边缘的距离.
参考答案
1.(1),
(2)
(3)①;②
1)根据在抛物线上建立方程组求解并将解析式整理成的形式即可得解;
(2)先求出直线的解解式,进而设,根据题意得到点在中垂线上,进而由中垂线性质(若为中垂线,则且与交点为中点)解得,得到,根据点在抛物线上即可建立方程求解;
(3)①取,表示任意位置的小树高,令解得横坐标,即可求解;
②设,根据题意得到直线与抛物线在区间上有两交点,为靠左一点的横坐标,注意到,即可结合一元二次方程求根公式通过计算求解;
(1)解:点,点在抛物线上,
∴,
解得:,
∴抛物线方程为,
∴抛物线的顶点坐标为;
(2)解:∵点,点在轴上,
∴,
∵,,
∴设直线的解析式为,即,解得:,
故直线的解析式为,
∵点在直线上,
设,,
∵轴,
∴点在中垂线上,故,
解得:,
∴,
∵点在抛物线上,
∴,整理得:,
解得:(舍)或,此时,
∴.
(3)解:①令,
则表示小树高,
∵,即,
∴,整理得,
解得:,
∵在左侧,故,,
∴.
②设,则在上有两解,且为其中较小解,
即直线与抛物线在上有两交点,
当时,,
令,得或(舍去),
∴,
又,
对称轴为,
为直线与抛物线两交点中靠左一点的横坐标,故,
综上,;
2.(1);
(2)20米.
(1)解:如图,建立平面直角坐标系,过作于,
则,,,,
∴,
∴,,
∵,
∴米,
∴,
∴,
设抛物线的解析式为,则有:
,
解得,
∴抛物线的函数表达式为;
(2)当时,,
解得:,,
∴,
∵海报为正方形,海报顶边的两个顶点恰好在钢拱圈上的A,B两点,
∴海报底边与桥面的距离为.
3.(1)
(2)
(1)如图,延长交轴于点,则,
,
,,
,
,
,
∵水路到达的最大高度是米,且恰好经过小树的顶端点,则点为抛物线的顶点,
∴设抛物线解析式为
将代入得
解得:
∴抛物线解析式为
(2)由(1)知, 设直线的解析式为则 ,
解得:,
,
如图,设 ,则,
,
,
,
∵轴,
,
,
,
,
∴当 时,取得最大值 ,
答:的最大值为
4.(1)坐标系见解析,y= x2+x
(2)不能
(1)建立平面直角坐标系如图,
∵顶点B的坐标是(9,12),
∴设抛物线的解析式为y=a(x-9)2+12,
∵点O的坐标是(0,0)
∴把点O的坐标代入得:
0=a(0-9)2+12,
解得a= ,
∴抛物线的解析式为y= (x-9)2+12
即y= x2+x;
(2)在Rt△AOC中,
∵∠AOC=30°,OA=8,
∴AC=OA sin30°=8×=4,
OC=OA cos30°=8×=12.
∴点A的坐标为(12,4),
∵当x=12时,y=,
∴这一杆不能把高尔夫球从O点直接打入球洞A点.
5.(1)
(2)
(3)
(1)解:∵,杯子的高度(即,之间的距离)为.
∴,,
设抛物线的解析式为,
∴,
解得,
∴抛物线的解析式为.
(2)解:∵抛物线的解析式为,
∴平移后的解析式为.
∴抛物线的对称轴为直线,
当时,,
∴,
∴的对称点为,
∵点D平移前坐标为,
∴平移后,
设直线的解析式为,
∴,
解得;
∴;
设直线的解析式为,
∴,
解得;
∴,
根据题意,喝过一次饮料后,发现剩余饮料的液面低于点,
∴.
(3)解:根据题意,以的中点O为原点,所在直线为x轴,所在直线为y轴建立平面直角坐标系;,
设与轴的交点为M,直线与轴的交点为S,
∵,杯子的高度(即,之间的距离)为.
∴,,
∵水平桌面上的装有饮料的高脚杯绕点顺时针旋转,
∴,
∵,
∴,
∴,
∴,
∴.
∵抛物线的解析式为,
设点N是抛物线上的一点,且,;
过点N作轴,交于点G,
∵水平桌面上的装有饮料的高脚杯绕点顺时针旋转,
∴,
∵,
∴,
过点G作轴于点E,
∵轴,
∴,,
∴,
∴,
∴,
∴
,
∵,,
∴时,取得最大值,且最大值为,
过点N作于点H,
则,
故的最大值为,
故液体的最大深度为.
6.(1)
(2)
(3)
(1)解:由题意得,在第一象限内的抛物线顶点的坐标,故设抛物线解析式为,
将代入得,
解得,,
在第一象限内的抛物线解析式为;
(2)解:当时,,
解得:,,
的取值范围是;
故答案为:.
(3)解:∵直线的解析式为:,
∴把代入得:,
把代入得:,解得:,
∴,,
∴,,
设平行于直线且与抛物线只有一个交点的直线的解析式为,
联立,即,
整理得:,
令,
解得,
∴直线的解析式为,
如图,设直线与轴的交点为,
把代入得:,
解得:,
则,
∴,
∵,
∴直线到直线的距离为,
根据题意得:光线与抛物线水流之间的距离为光线与抛物线水流之间的最小垂直距离,即直线到直线的距离,
∴光线与抛物线水流之间的距离为.
7.任务一:
任务二:
任务三:薄膜与地面接触点与喷水口的水平距离为8.7米
解:任务一:根据题意得最高点,
设水柱所在抛物线的函数解析式为:.
由题意得:抛物线经过点D的坐标为.
∴,解得a,
∴水柱所在抛物线的函数解析式为:;
任务二:当时,.
解得:.
∴.
任务三:
薄膜所在平面可看成是一条直线.
∵薄膜所在平面和地面的夹角是,
∴薄膜所在平面的直线解析式为:.
当薄膜所在直线与水柱所在抛物线相切时,
,
∴.
∵只有一个交点,
∴,解得.
∴.
∴直线与x轴的交点为.
过点于点M,且,过点F作,交x轴于点.
∴.
由题意得:,
∴(米).
∴(米)
答:薄膜与地面接触点与喷水口的水平距离为8.7米.
8.(1)2,3.6
(2)
(3)明明在此次考试中能得到满分,见解析
(4)点C的坐标为
长线于点F,证明出,得到,设,表示出,,,,然后代入求出,然后求出,所在直线表达式为,然后和抛物线联立求解即可.
(1)解:由题意可知出手时实心球的竖直高度即为时y的值,
通过图表可得当时,,
得在明明投掷过程中,出手时实心球的竖直高度是2米,
由当时,;当时,,
可得对称轴为直线,
则当时,实心球在空中取得最大高度,
通过图表可得当时,,
得实心球在空中的最大高度是3.6米,
故答案为:2,3.6;
(2)解:设抛物线的解析式为,
由(1)得抛物线的顶点坐标为,
则,
得抛物线的解析式为,
把代入,
得,
解得,
∴抛物线的解析式为;
(3)解:明明在此次考试中能得到满分,理由如下:
把代入,
得,
解得或(不符合题意,舍去),
∵,
∴明明在此次考试中能得到满分.
(4)如图所示,
过点B作,过点E作轴交y轴于点D,过点B作交延长线于点F,
∵
∴
∵
∴
∵
∴
∴
∵
∴
∴
设
∵,点
∴,,,
∴
解得
∴
设,所在直线表达式为
∴
∴解得
∴,所在直线表达式为
∴联立和抛物线得,
整理得,
解得(舍去)或
∴将代入
∴点C的坐标为.
9.(1)米
(2)①;②大于或等于,小于
(1)解:乙运动员的第一次的运动高度与运动时间的二次函数图象经过点 ,点D ,点,设其解析式为:,
∴,解得:,即乙运动员的第一次的运动高度与运动时间的二次函数解析式为:,
因为所有二次函数图象开口大小相同.设,把点B 代入得:
,解得:
∴,即,故
甲运动员在这次训练中运动的最大高度是米,时间是秒.
(2)当秒时,,
即乙二次起跳中,当秒时,其高度,设乙二次起跳中的解析式为,将点A 和代入得:
,解得:,即,
∵,
∴点,
∴设直线DE解析式为,
得,解得:,
∴设直线解析式为,
②延长交x轴于,过点D作轴,
点D的坐标为,
∴,,
当时,,
∴,点K的坐标为,
∴直线,
设乙二次起跳中的解析式为,把点A 代入得:,
∴,
所以,
当时,,,
当时, ,
∴,
∴,整理得:,
∴(不合题意舍去),,
当,,
∵,
故,随增大而增大;
故乙在第二次蹦床运动中最大运动高度的取值范围大于或等于,小于.
10.(1)
(2)
(3)
(4)米
(1)解:设此时抛物线的表达式为,
根据题意,抛物线过点和点,
则,
解得:,
∴此时抛物线的表达式为;
(2)解:∵,
∴抛物线图象的对称轴为,
∵直线关于轴对称的直线为,,
抛物线关于轴对称的抛物线图象的对称轴为,
即抛物线关于轴对称的抛物线解析式为:,
再将抛物线:向右平移8个单位得到,
∴喷出的水柱形成的抛物线的表达式:;
(3)解:如图,
根据题意喷出的水柱形成的抛物线图象的对称轴为,与x轴的一个交点,
∴顶点坐标为,
∵,
∴与x轴的一个交点坐标为,
设喷出的水柱形成的抛物线表达式为:,
将点代入,得,
解得:,
∴喷出的水柱形成的抛物线表达式为:,
同理,喷出的水柱形成的抛物线的图象过点,
则喷出的水柱形成的抛物线的表达式为:,
令,
解得:,则,
∴汇聚点的坐标为;
(4)解:设直线的方程为,与直线平行的直线的方程为,
∴联立,得,
∴,
由题意知:直线与抛物线相切时,水柱上的点到相应射灯所在直线的距离最小,
故,即,
∴,
如图,设直线与抛物线切于点K,过点K作的平行线,过点作轴交于点F,
则,
又厘米,
∴在中,厘米,
∴直线可以看成是将直线向左平移个单位得到,
即直线,
令,则,
∴,
∵,
∴米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
