山东省德州市夏津县万隆中学2016届九年级(下)月考数学试卷(4月份)(解析版)
文档属性
| 名称 | 山东省德州市夏津县万隆中学2016届九年级(下)月考数学试卷(4月份)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 188.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-11 15:58:32 | ||
图片预览

文档简介
2015-2016学年山东省德州市夏津县万隆中学九年级(下)月考数学试卷(4月份)
一.选择题(每题3分)
1.下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
2.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
3.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.csinA=a B.bcosB=c C.atanA=b D.ctanB=b
4.如图,在矩形ABCD中,点E在AB边 ( http: / / www.21cnjy.com )上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A. B. C. D.
5.抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
6.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
7.点M(2,﹣1)向上平移2个单位长度得到的点的坐标是( )
A.(2,0) B.(2,1) C.(2,2) D.(2,﹣3)
8.若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°
9.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
10.已知:如图,在Rt△ABC中,∠AC ( http: / / www.21cnjy.com )B=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
A.30° B.40° C.50° D.60°
二.填空题(每题4分)
11.如图,菱形ABCD中,对角线AC=6 ( http: / / www.21cnjy.com ),BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .
12.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= .
13.如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 .
14.如图,抛物线y=x2 ( http: / / www.21cnjy.com )在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….
则顶点M2014的坐标为( , ).
三.解答题(共6小题,76分)
15.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cosA=.
求(1)DE、CD的长;(2)tan∠DBC的值.
16.如图,直角梯形纸片ABCD中,A ( http: / / www.21cnjy.com )D∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.
17.如图,二次函数y=ax2+bx+c的图象过A、B、C三点.
(1)求出抛物线解析式和顶点坐标;
(2)当﹣2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
18.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
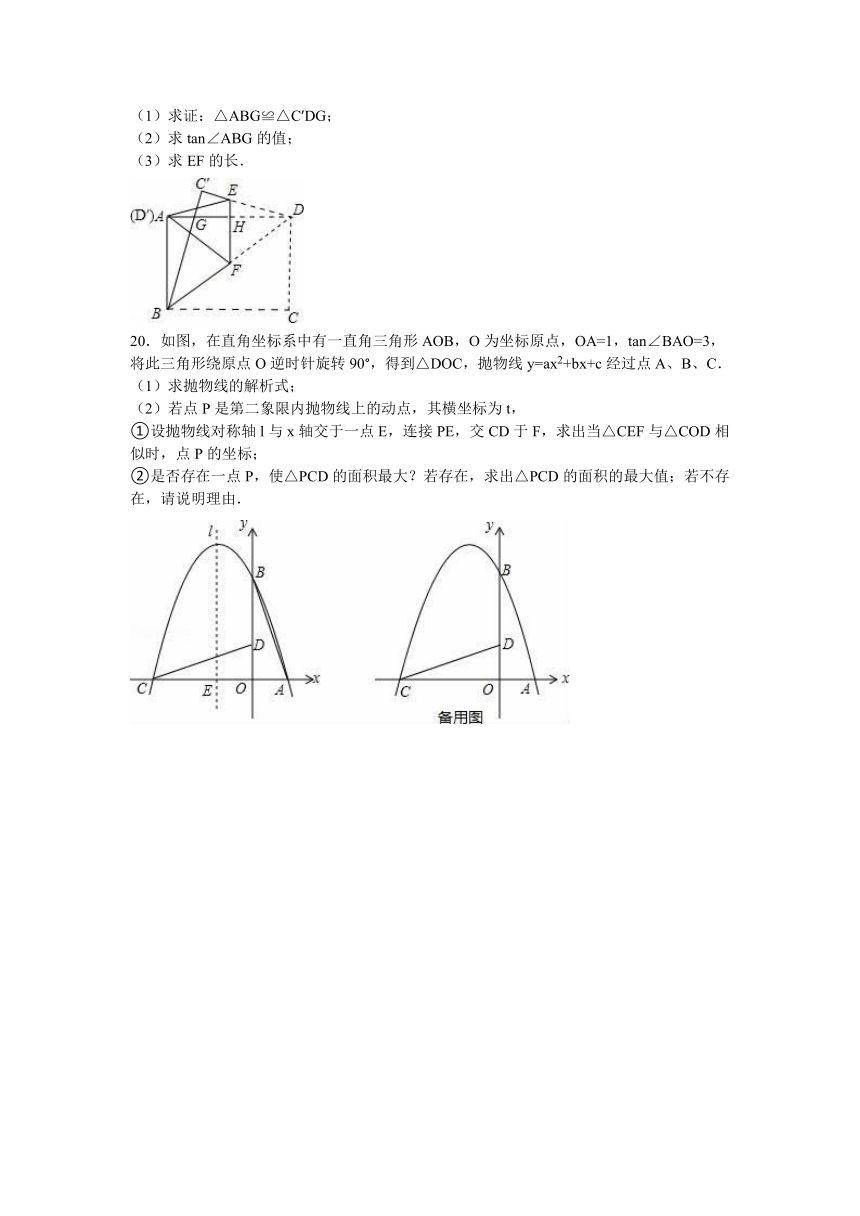
19.如图,在矩形纸片ABCD中, ( http: / / www.21cnjy.com )AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
20.如图,在直角坐标系中有一直角 ( http: / / www.21cnjy.com )三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
2015-2016学年山东省德州市夏津县万隆中学九年级(下)月考数学试卷(4月份)
参考答案与试题解析
一.选择题(每题3分)
1.下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
【考点】轴对称图形.
【分析】根据轴对称图形及对称轴的定义求解.
【解答】解:第一个是轴对称图形,有2条对称轴;
第二个是轴对称图形,有2条对称轴;
第三个是轴对称图形,有2条对称轴;
第四个是轴对称图形,有3条对称轴;
∴对称轴的条数为2的图形的个数是3;
故选:C.
2.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
【考点】二次函数的最值.
【分析】根据对称轴的位置,分三种情况讨论求解即可.
【解答】解:二次函数的对称轴为直线x=m,
①m<﹣2时,x=﹣2时二次函数有最大值,
此时﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,与m<﹣2矛盾,故m值不存在;
②当﹣2≤m≤1时,x=m时,二次函数有最大值,
此时,m2+1=4,
解得m=﹣,m=(舍去);
③当m>1时,x=1时二次函数有最大值,
此时,﹣(1﹣m)2+m2+1=4,
解得m=2,
综上所述,m的值为2或﹣.
故选:C.
3.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.csinA=a B.bcosB=c C.atanA=b D.ctanB=b
【考点】勾股定理的逆定理;锐角三角函数的定义.
【分析】由于a2+b2=c2,根据勾股定理的逆定理得到△ABC是直角三角形,且∠C=90°,再根据锐角三角函数的定义即可得到正确选项.
【解答】解:∵a2+b2=c2,
∴△ABC是直角三角形,且∠C=90°.
A、sinA=,则csinA=a.故本选项正确;
B、cosB=,则cosBc=a.故本选项错误;
C、tanA=,则=b.故本选项错误;
D、tanB=,则atanB=b.故本选项错误.
故选A.
4.如图,在矩形ABCD中,点E在AB边上, ( http: / / www.21cnjy.com )沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A. B. C. D.
【考点】翻折变换(折叠问题);矩形的性质;锐角三角函数的定义.
【分析】由四边形ABCD是 ( http: / / www.21cnjy.com )矩形,可得:∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,由折叠的性质可得:∠EFC=∠B=90°,CF=BC=5,由同角的余角相等,即可得∠DCF=∠AFE,然后在Rt△DCF中,即可求得答案.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,
由题意得:∠EFC=∠B=90°,CF=BC=5,
∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,
∴∠DCF=∠AFE,
∵在Rt△DCF中,CF=5,CD=4,
∴DF=3,
∴tan∠AFE=tan∠DCF==.
故选C.
5.抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
【考点】二次函数图象与几何变换.
【分析】根据“左加右减,上加下减”的原则进行解答即可.
【解答】解:抛物线y=x2向左平移2个单位可得到抛物线y=(x+2)2,
抛物线y=(x+2)2,再向下平移3个单位即可得到抛物线y=(x+2)2﹣3.
故平移过程为:先向左平移2个单位,再向下平移3个单位.
故选:B.
6.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【考点】二次函数图象与系数的关系.
【分析】由函数y=x2+ ( http: / / www.21cnjy.com )bx+c与x轴无交点,可得b2﹣4c<0;当x=1时,y=1+b+c=1;当x=3时,y=9+3b+c=3;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
【解答】解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4ac<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故④正确.
故选B
7.点M(2,﹣1)向上平移2个单位长度得到的点的坐标是( )
A.(2,0) B.(2,1) C.(2,2) D.(2,﹣3)
【考点】坐标与图形变化-平移.
【分析】根据向上平移,横坐标不变,纵坐标相加进行解答.
【解答】解:∵点M(2,﹣1)向上平移2个单位长度,
∴﹣1+2=1,
∴平移后的点坐标是(2,1).
故选:B.
8.若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°
【考点】角的计算.
【分析】先画出图形,利用角的和差关系计算.
【解答】解:∵∠AOB=60°,∠BOD=15°,
∴∠AOD=∠AOB﹣∠BOD=60°﹣15°=45°,
故选:C.
9.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
【考点】平移的性质.
【分析】根据平移的基本性质,得出四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC即可得出答案.
【解答】解:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC;
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
故选:C.
10.已知:如图,在Rt△ABC中,∠ ( http: / / www.21cnjy.com )ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
A.30° B.40° C.50° D.60°
【考点】翻折变换(折叠问题).
【分析】根据折叠的性质可知,折叠前后的两个三角形全等,则∠D=∠A,∠MCD=∠MCA,从而求得答案.
【解答】解:∵在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,
∴AM=MC=BM,
∴∠A=∠MCA,
∵将△ACM沿直线CM折叠,点A落在点D处,
∴CM平分∠ACD,∠A=∠D,
∴∠ACM=∠MCD,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∵∠A+∠B=90°,
∴∠A=∠BCD,
∴∠BCD=∠DCM=∠MCA=30°
∴∠A=30°.
故选:A.
二.填空题(每题4分)
11.如图,菱形ABCD中,对角线AC ( http: / / www.21cnjy.com )=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 5 .
【考点】轴对称-最短路线问题;勾股定理的应用;平行四边形的判定与性质;菱形的性质.
【分析】作M关于BD的对称点Q,连 ( http: / / www.21cnjy.com )接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【解答】解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:5.
12.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= 55° .
【考点】旋转的性质.
【分析】根据题意得出∠ACA′=35°,则∠A′=90°﹣35°=55°,即可得出∠A的度数.
【解答】解:∵把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D,∠A′DC=90°,
∴∠ACA′=35°,则∠A′=90°﹣35°=55°,
则∠A=∠A′=55°.
故答案为:55°.
13.如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 2 .
【考点】旋转的性质;等边三角形的性质.
【分析】由在等边三角形ABC中,AB=6 ( http: / / www.21cnjy.com ),D是BC上一点,且BC=3BD,根据等边三角形的性质,即可求得BD的长,然后由旋转的性质,即可求得CE的长度.
【解答】解:∵在等边三角形ABC中,AB=6,
∴BC=AB=6,
∵BC=3BD,
∴BD=BC=2,
∵△ABD绕点A旋转后得到△ACE,
∴△ABD≌△ACE,
∴CE=BD=2.
故答案为:2.
14.如图,抛物线y=x2在第一象限 ( http: / / www.21cnjy.com )内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….
则顶点M2014的坐标为( 4027 , 4027 ).
【考点】二次函数图象与几何变换.
【分析】根据抛物线y=x2与抛物线yn=(x﹣an)2+an相交于An,可发现规律,根据规律,可得答案.
【解答】解:M1(a1,a1)是抛物线y1=(x﹣a1)2+a1的顶点,
抛物线y=x2与抛物线y1=(x﹣a1)2+a1相交于A1,
得x2=(x﹣a1)2+a1,
即2a1x=a12+a1,
x=(a1+1).
∵x为整数点
∴a1=1,
M1(1,1);
M2(a2,a2)是抛物线y2=(x﹣a2)2+a2=x2﹣2a2x+a22+a2顶点,
抛物线y=x2与y2相交于A2,
x2=x2﹣2a2x+a22+a2,
∴2a2x=a22+a2,
x=(a2+1).
∵x为整数点,
∴a2=3,
M2(3,3),
M3(a3,a3)是抛物线y2=(x﹣a3)2+a3=x2﹣2a3x+a32+a3顶点,
抛物线y=x2与y3相交于A3,
x2=x2﹣2a3x+a32+a3,
∴2a3x=a32+a3,
x=(a3+1).
∵x为整数点
∴a3=5,
M3(5,5),
∴点M2014,两坐标为:2014×2﹣1=4027,
∴M2014,
故答案为:
三.解答题(共6小题,76分)
15.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cosA=.
求(1)DE、CD的长;(2)tan∠DBC的值.
【考点】解直角三角形;角平分线的性质;勾股定理;相似三角形的判定与性质.
【分析】(1)由DE⊥AB,AE=6,cosA=,可求出AD的长,根据勾股定理可求出DE的长,由角平分线的性质可得DC=DE=8;
(2)由AD=10,DC=8,得AC= ( http: / / www.21cnjy.com )AD+DC=18.由∠A=∠A,∠AED=∠ACB,可知△ADE∽△ABC,由相似三角形边长的比可求出BC的长,根据三角函数的定义可求出tan∠DBC=.
【解答】解:(1)在Rt△ADE中,由AE=6,cosA==,得:AD=10,
由勾股定理得DE===8
∵BD平分∠ABC,DE⊥AB,∠C=90°,角平分线性质得:DC=DE=8.
(2)方法一:由(1)AD=10,DC=8,得:AC=AD+DC=18.
在△ADE与△ABC,∠A=∠A,∠AED=∠ACB,
∴△ADE∽△ABC得: =,即=,BC=24,
得:tan∠DBC===
方法二:由(1)得AC=18,又cosA==,得AB=30,
由勾股定理得BC=24得:tan∠DBC=.
16.如图,直角梯形纸片ABC ( http: / / www.21cnjy.com )D中,AD∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.
【考点】直角梯形;翻折变换(折叠问题);解直角三角形.
【分析】(1)利用等边对等角可以得到∠FBC=∠C=30°,再利用折叠的性质可以得到∠EBF=∠CBF=30°,从而可以求得所求角的度数.
(2)利用上题得到的结论可以求得线段BD,然后在直角三角形ABD中求得AB即可.
【解答】解:(1)∵BF=CF=8,
∴∠FBC=∠C=30°,
∵折叠纸片使BC经过点D,点C落在点E处,BF是折痕,
∴∠EBF=∠CBF=30°,
∴∠EBC=60°,
∴∠BDF=90°;
(2)∵∠EBC=60°
∴∠ADB=60°,
∵BF=CF=8.
∴BD=BF sin60°=4
∴在Rt△BAD中,
AB=BD×sin60°=6.
17.如图,二次函数y=ax2+bx+c的图象过A、B、C三点.
(1)求出抛物线解析式和顶点坐标;
(2)当﹣2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
【考点】二次函数图象上点的坐标特征;二次函数的性质.
【分析】(1)根据图象得A(﹣1,0) ( http: / / www.21cnjy.com ),B(0,﹣3),C(4,5),代入y=ax2+bx+c中,解方程组可求a、b、c的值,从而确定顶点坐标;
(2)根据对称轴(顶点)的位置,开口方向,确定当﹣2<x<2时,y的最大值和最小值;
(3)已知抛物线与x轴交于A(﹣1,0),对称轴为x=1,可求抛物线与x轴的另一交点坐标,结合开口方向判断当y>0时,x的取值范围.
【解答】解:(1)将A(﹣1,0),B(0,﹣3),C(4,5)代入y=ax2+bx+c中,得
,解得
∴抛物线解析式为:y=x2﹣2x﹣3,即y=(x﹣1)2﹣4,顶点坐标为(1,﹣4);
(2)∵对称轴x=1,开口向上,
∴当﹣2<x<2时,y有最小值为﹣4,
x=﹣2时,对应点离对称轴较远,函数有最大值为5,
∴﹣4≤y<5;
(3)∵抛物线经过A(﹣1,0),对称轴为x=1,
∴抛物线与x轴的另一交点为(3,0),
又抛物线开口向上,
∴当x>3或x<﹣1时,y>0.
18.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
【考点】二次函数的应用.
【分析】(1)根据单价乘以数量,可得利润,可得答案;
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;
(3)根据二次函数值大于或等于4800,一次函数值大于或等于48000,可得不等式,根据解不等式组,可得答案.
【解答】解:(1)当1≤x<50时,y=(x+40﹣30)=﹣2x2+180x+2000,
当50≤x≤90时,
y=(90﹣30)=﹣120x+12000,
综上所述:y=;
(2)当1≤x<50时,
y=﹣2x2+180x+2000,
y=﹣2(x﹣45)2+6050.
∴a=﹣2<0,
∴二次函数开口下,二次函数对称轴为x=45,
当x=45时,y最大=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)①当1≤x<50时,y=﹣2x2+180x+2000≥4800,
解得:20≤x<70,
因此利润不低于4800元的天数是20≤x<50,共30天;
②当50≤x≤90时,y=﹣120x+12000≥4800,
解得:x≤60,
因此利润不低于4800元的天数是50≤x≤60,共11天,
所以该商品在整个销售过程中,共41天每天销售利润不低于4800元.
19.如图,在矩形纸片ABCD中,AB=6 ( http: / / www.21cnjy.com ),BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;矩形的性质;解直角三角形.
【分析】(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;
(2)由(1)可知GD=GB ( http: / / www.21cnjy.com ),故AG+GB=AD,设AG=x,则GB=8﹣x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知 ( http: / / www.21cnjy.com )EF垂直平分AD,故HD=AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
【解答】(1)证明:∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵,
∴△ABG≌△C′DG(AAS);
(2)解:
∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,
设AG=x,则GB=8﹣x,
在Rt△ABG中,
∵AB2+AG2=BG2,
即62+x2=(8﹣x)2,
解得x=,
∴tan∠ABG===;
(3)解:
∵△AEF是△DEF翻折而成,
∴EF垂直平分AD,
∴HD=AD=4,
∴tan∠ABG=tan∠ADE=,
∴EH=HD×=4×=,
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF=AB=×6=3,
∴EF=EH+HF=+3=.
20.如图,在直角坐标系中有一直角三角 ( http: / / www.21cnjy.com )形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)先求出A、B、C的坐标,再运用待定系数法就可以直接求出二次函数的解析式;
(2)①由(1)的解析式可以求出抛物线的 ( http: / / www.21cnjy.com )对称轴,分类讨论当∠CEF=90°时,当∠CFE=90°时,根据相似三角形的性质就可以求出P点的坐标;
②先运用待定系数法求出直线CD的解析式,设P ( http: / / www.21cnjy.com )M与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN就可以表示出三角形PCD的面积,运用顶点式就可以求出结论.
【解答】解:(1)在Rt△AOB中,OA=1,tan∠BAO==3,
∴OB=3OA=3.
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB,
∴OC=OB=3,OD=OA=1,
∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).
代入解析式为
,
解得:.
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)①∵抛物线的解析式为y=﹣x2﹣2x+3,
∴对称轴l=﹣=﹣1,
∴E点的坐标为(﹣1,0).
如图,当∠CEF=90°时,△CEF∽△COD.此时点P在对称轴上,即点P为抛物线的顶点,P(﹣1,4);
当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.
∴,
∴MP=3EM.
∵P的横坐标为t,
∴P(t,﹣t2﹣2t+3).
∵P在第二象限,
∴PM=﹣t2﹣2t+3,EM=﹣1﹣t,
∴﹣t2﹣2t+3=﹣(t﹣1)(t+3),
解得:t1=﹣2,t2=﹣3(因为P与C重合,所以舍去),
∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.
∴P(﹣2,3).
∴当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3);
②设直线CD的解析式为y=kx+b,由题意,得
,
解得:,
∴直线CD的解析式为:y=x+1.
设PM与CD的交点为N,则点N的坐标为(t, t+1),
∴NM=t+1.
∴PN=PM﹣NM=﹣t2﹣2t+3﹣(t+1)=﹣t2﹣+2.
∵S△PCD=S△PCN+S△PDN,
∴S△PCD=PN CM+PN OM
=PN(CM+OM)
=PN OC
=×3(﹣t2﹣+2)
=﹣(t+)2+,
∴当t=﹣时,S△PCD的最大值为.
2016年5月11日
一.选择题(每题3分)
1.下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
2.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
3.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.csinA=a B.bcosB=c C.atanA=b D.ctanB=b
4.如图,在矩形ABCD中,点E在AB边 ( http: / / www.21cnjy.com )上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A. B. C. D.
5.抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
6.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
7.点M(2,﹣1)向上平移2个单位长度得到的点的坐标是( )
A.(2,0) B.(2,1) C.(2,2) D.(2,﹣3)
8.若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°
9.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
10.已知:如图,在Rt△ABC中,∠AC ( http: / / www.21cnjy.com )B=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
A.30° B.40° C.50° D.60°
二.填空题(每题4分)
11.如图,菱形ABCD中,对角线AC=6 ( http: / / www.21cnjy.com ),BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .
12.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= .
13.如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 .
14.如图,抛物线y=x2 ( http: / / www.21cnjy.com )在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….
则顶点M2014的坐标为( , ).
三.解答题(共6小题,76分)
15.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cosA=.
求(1)DE、CD的长;(2)tan∠DBC的值.
16.如图,直角梯形纸片ABCD中,A ( http: / / www.21cnjy.com )D∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.
17.如图,二次函数y=ax2+bx+c的图象过A、B、C三点.
(1)求出抛物线解析式和顶点坐标;
(2)当﹣2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
18.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
19.如图,在矩形纸片ABCD中, ( http: / / www.21cnjy.com )AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
20.如图,在直角坐标系中有一直角 ( http: / / www.21cnjy.com )三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
2015-2016学年山东省德州市夏津县万隆中学九年级(下)月考数学试卷(4月份)
参考答案与试题解析
一.选择题(每题3分)
1.下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
【考点】轴对称图形.
【分析】根据轴对称图形及对称轴的定义求解.
【解答】解:第一个是轴对称图形,有2条对称轴;
第二个是轴对称图形,有2条对称轴;
第三个是轴对称图形,有2条对称轴;
第四个是轴对称图形,有3条对称轴;
∴对称轴的条数为2的图形的个数是3;
故选:C.
2.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
【考点】二次函数的最值.
【分析】根据对称轴的位置,分三种情况讨论求解即可.
【解答】解:二次函数的对称轴为直线x=m,
①m<﹣2时,x=﹣2时二次函数有最大值,
此时﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,与m<﹣2矛盾,故m值不存在;
②当﹣2≤m≤1时,x=m时,二次函数有最大值,
此时,m2+1=4,
解得m=﹣,m=(舍去);
③当m>1时,x=1时二次函数有最大值,
此时,﹣(1﹣m)2+m2+1=4,
解得m=2,
综上所述,m的值为2或﹣.
故选:C.
3.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.csinA=a B.bcosB=c C.atanA=b D.ctanB=b
【考点】勾股定理的逆定理;锐角三角函数的定义.
【分析】由于a2+b2=c2,根据勾股定理的逆定理得到△ABC是直角三角形,且∠C=90°,再根据锐角三角函数的定义即可得到正确选项.
【解答】解:∵a2+b2=c2,
∴△ABC是直角三角形,且∠C=90°.
A、sinA=,则csinA=a.故本选项正确;
B、cosB=,则cosBc=a.故本选项错误;
C、tanA=,则=b.故本选项错误;
D、tanB=,则atanB=b.故本选项错误.
故选A.
4.如图,在矩形ABCD中,点E在AB边上, ( http: / / www.21cnjy.com )沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A. B. C. D.
【考点】翻折变换(折叠问题);矩形的性质;锐角三角函数的定义.
【分析】由四边形ABCD是 ( http: / / www.21cnjy.com )矩形,可得:∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,由折叠的性质可得:∠EFC=∠B=90°,CF=BC=5,由同角的余角相等,即可得∠DCF=∠AFE,然后在Rt△DCF中,即可求得答案.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,
由题意得:∠EFC=∠B=90°,CF=BC=5,
∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,
∴∠DCF=∠AFE,
∵在Rt△DCF中,CF=5,CD=4,
∴DF=3,
∴tan∠AFE=tan∠DCF==.
故选C.
5.抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
【考点】二次函数图象与几何变换.
【分析】根据“左加右减,上加下减”的原则进行解答即可.
【解答】解:抛物线y=x2向左平移2个单位可得到抛物线y=(x+2)2,
抛物线y=(x+2)2,再向下平移3个单位即可得到抛物线y=(x+2)2﹣3.
故平移过程为:先向左平移2个单位,再向下平移3个单位.
故选:B.
6.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【考点】二次函数图象与系数的关系.
【分析】由函数y=x2+ ( http: / / www.21cnjy.com )bx+c与x轴无交点,可得b2﹣4c<0;当x=1时,y=1+b+c=1;当x=3时,y=9+3b+c=3;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
【解答】解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4ac<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故④正确.
故选B
7.点M(2,﹣1)向上平移2个单位长度得到的点的坐标是( )
A.(2,0) B.(2,1) C.(2,2) D.(2,﹣3)
【考点】坐标与图形变化-平移.
【分析】根据向上平移,横坐标不变,纵坐标相加进行解答.
【解答】解:∵点M(2,﹣1)向上平移2个单位长度,
∴﹣1+2=1,
∴平移后的点坐标是(2,1).
故选:B.
8.若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°
【考点】角的计算.
【分析】先画出图形,利用角的和差关系计算.
【解答】解:∵∠AOB=60°,∠BOD=15°,
∴∠AOD=∠AOB﹣∠BOD=60°﹣15°=45°,
故选:C.
9.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
【考点】平移的性质.
【分析】根据平移的基本性质,得出四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC即可得出答案.
【解答】解:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC;
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
故选:C.
10.已知:如图,在Rt△ABC中,∠ ( http: / / www.21cnjy.com )ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
A.30° B.40° C.50° D.60°
【考点】翻折变换(折叠问题).
【分析】根据折叠的性质可知,折叠前后的两个三角形全等,则∠D=∠A,∠MCD=∠MCA,从而求得答案.
【解答】解:∵在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,
∴AM=MC=BM,
∴∠A=∠MCA,
∵将△ACM沿直线CM折叠,点A落在点D处,
∴CM平分∠ACD,∠A=∠D,
∴∠ACM=∠MCD,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∵∠A+∠B=90°,
∴∠A=∠BCD,
∴∠BCD=∠DCM=∠MCA=30°
∴∠A=30°.
故选:A.
二.填空题(每题4分)
11.如图,菱形ABCD中,对角线AC ( http: / / www.21cnjy.com )=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 5 .
【考点】轴对称-最短路线问题;勾股定理的应用;平行四边形的判定与性质;菱形的性质.
【分析】作M关于BD的对称点Q,连 ( http: / / www.21cnjy.com )接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【解答】解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:5.
12.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= 55° .
【考点】旋转的性质.
【分析】根据题意得出∠ACA′=35°,则∠A′=90°﹣35°=55°,即可得出∠A的度数.
【解答】解:∵把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D,∠A′DC=90°,
∴∠ACA′=35°,则∠A′=90°﹣35°=55°,
则∠A=∠A′=55°.
故答案为:55°.
13.如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 2 .
【考点】旋转的性质;等边三角形的性质.
【分析】由在等边三角形ABC中,AB=6 ( http: / / www.21cnjy.com ),D是BC上一点,且BC=3BD,根据等边三角形的性质,即可求得BD的长,然后由旋转的性质,即可求得CE的长度.
【解答】解:∵在等边三角形ABC中,AB=6,
∴BC=AB=6,
∵BC=3BD,
∴BD=BC=2,
∵△ABD绕点A旋转后得到△ACE,
∴△ABD≌△ACE,
∴CE=BD=2.
故答案为:2.
14.如图,抛物线y=x2在第一象限 ( http: / / www.21cnjy.com )内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….
则顶点M2014的坐标为( 4027 , 4027 ).
【考点】二次函数图象与几何变换.
【分析】根据抛物线y=x2与抛物线yn=(x﹣an)2+an相交于An,可发现规律,根据规律,可得答案.
【解答】解:M1(a1,a1)是抛物线y1=(x﹣a1)2+a1的顶点,
抛物线y=x2与抛物线y1=(x﹣a1)2+a1相交于A1,
得x2=(x﹣a1)2+a1,
即2a1x=a12+a1,
x=(a1+1).
∵x为整数点
∴a1=1,
M1(1,1);
M2(a2,a2)是抛物线y2=(x﹣a2)2+a2=x2﹣2a2x+a22+a2顶点,
抛物线y=x2与y2相交于A2,
x2=x2﹣2a2x+a22+a2,
∴2a2x=a22+a2,
x=(a2+1).
∵x为整数点,
∴a2=3,
M2(3,3),
M3(a3,a3)是抛物线y2=(x﹣a3)2+a3=x2﹣2a3x+a32+a3顶点,
抛物线y=x2与y3相交于A3,
x2=x2﹣2a3x+a32+a3,
∴2a3x=a32+a3,
x=(a3+1).
∵x为整数点
∴a3=5,
M3(5,5),
∴点M2014,两坐标为:2014×2﹣1=4027,
∴M2014,
故答案为:
三.解答题(共6小题,76分)
15.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cosA=.
求(1)DE、CD的长;(2)tan∠DBC的值.
【考点】解直角三角形;角平分线的性质;勾股定理;相似三角形的判定与性质.
【分析】(1)由DE⊥AB,AE=6,cosA=,可求出AD的长,根据勾股定理可求出DE的长,由角平分线的性质可得DC=DE=8;
(2)由AD=10,DC=8,得AC= ( http: / / www.21cnjy.com )AD+DC=18.由∠A=∠A,∠AED=∠ACB,可知△ADE∽△ABC,由相似三角形边长的比可求出BC的长,根据三角函数的定义可求出tan∠DBC=.
【解答】解:(1)在Rt△ADE中,由AE=6,cosA==,得:AD=10,
由勾股定理得DE===8
∵BD平分∠ABC,DE⊥AB,∠C=90°,角平分线性质得:DC=DE=8.
(2)方法一:由(1)AD=10,DC=8,得:AC=AD+DC=18.
在△ADE与△ABC,∠A=∠A,∠AED=∠ACB,
∴△ADE∽△ABC得: =,即=,BC=24,
得:tan∠DBC===
方法二:由(1)得AC=18,又cosA==,得AB=30,
由勾股定理得BC=24得:tan∠DBC=.
16.如图,直角梯形纸片ABC ( http: / / www.21cnjy.com )D中,AD∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.
【考点】直角梯形;翻折变换(折叠问题);解直角三角形.
【分析】(1)利用等边对等角可以得到∠FBC=∠C=30°,再利用折叠的性质可以得到∠EBF=∠CBF=30°,从而可以求得所求角的度数.
(2)利用上题得到的结论可以求得线段BD,然后在直角三角形ABD中求得AB即可.
【解答】解:(1)∵BF=CF=8,
∴∠FBC=∠C=30°,
∵折叠纸片使BC经过点D,点C落在点E处,BF是折痕,
∴∠EBF=∠CBF=30°,
∴∠EBC=60°,
∴∠BDF=90°;
(2)∵∠EBC=60°
∴∠ADB=60°,
∵BF=CF=8.
∴BD=BF sin60°=4
∴在Rt△BAD中,
AB=BD×sin60°=6.
17.如图,二次函数y=ax2+bx+c的图象过A、B、C三点.
(1)求出抛物线解析式和顶点坐标;
(2)当﹣2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
【考点】二次函数图象上点的坐标特征;二次函数的性质.
【分析】(1)根据图象得A(﹣1,0) ( http: / / www.21cnjy.com ),B(0,﹣3),C(4,5),代入y=ax2+bx+c中,解方程组可求a、b、c的值,从而确定顶点坐标;
(2)根据对称轴(顶点)的位置,开口方向,确定当﹣2<x<2时,y的最大值和最小值;
(3)已知抛物线与x轴交于A(﹣1,0),对称轴为x=1,可求抛物线与x轴的另一交点坐标,结合开口方向判断当y>0时,x的取值范围.
【解答】解:(1)将A(﹣1,0),B(0,﹣3),C(4,5)代入y=ax2+bx+c中,得
,解得
∴抛物线解析式为:y=x2﹣2x﹣3,即y=(x﹣1)2﹣4,顶点坐标为(1,﹣4);
(2)∵对称轴x=1,开口向上,
∴当﹣2<x<2时,y有最小值为﹣4,
x=﹣2时,对应点离对称轴较远,函数有最大值为5,
∴﹣4≤y<5;
(3)∵抛物线经过A(﹣1,0),对称轴为x=1,
∴抛物线与x轴的另一交点为(3,0),
又抛物线开口向上,
∴当x>3或x<﹣1时,y>0.
18.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
【考点】二次函数的应用.
【分析】(1)根据单价乘以数量,可得利润,可得答案;
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;
(3)根据二次函数值大于或等于4800,一次函数值大于或等于48000,可得不等式,根据解不等式组,可得答案.
【解答】解:(1)当1≤x<50时,y=(x+40﹣30)=﹣2x2+180x+2000,
当50≤x≤90时,
y=(90﹣30)=﹣120x+12000,
综上所述:y=;
(2)当1≤x<50时,
y=﹣2x2+180x+2000,
y=﹣2(x﹣45)2+6050.
∴a=﹣2<0,
∴二次函数开口下,二次函数对称轴为x=45,
当x=45时,y最大=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)①当1≤x<50时,y=﹣2x2+180x+2000≥4800,
解得:20≤x<70,
因此利润不低于4800元的天数是20≤x<50,共30天;
②当50≤x≤90时,y=﹣120x+12000≥4800,
解得:x≤60,
因此利润不低于4800元的天数是50≤x≤60,共11天,
所以该商品在整个销售过程中,共41天每天销售利润不低于4800元.
19.如图,在矩形纸片ABCD中,AB=6 ( http: / / www.21cnjy.com ),BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;矩形的性质;解直角三角形.
【分析】(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;
(2)由(1)可知GD=GB ( http: / / www.21cnjy.com ),故AG+GB=AD,设AG=x,则GB=8﹣x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知 ( http: / / www.21cnjy.com )EF垂直平分AD,故HD=AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
【解答】(1)证明:∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵,
∴△ABG≌△C′DG(AAS);
(2)解:
∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,
设AG=x,则GB=8﹣x,
在Rt△ABG中,
∵AB2+AG2=BG2,
即62+x2=(8﹣x)2,
解得x=,
∴tan∠ABG===;
(3)解:
∵△AEF是△DEF翻折而成,
∴EF垂直平分AD,
∴HD=AD=4,
∴tan∠ABG=tan∠ADE=,
∴EH=HD×=4×=,
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF=AB=×6=3,
∴EF=EH+HF=+3=.
20.如图,在直角坐标系中有一直角三角 ( http: / / www.21cnjy.com )形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)先求出A、B、C的坐标,再运用待定系数法就可以直接求出二次函数的解析式;
(2)①由(1)的解析式可以求出抛物线的 ( http: / / www.21cnjy.com )对称轴,分类讨论当∠CEF=90°时,当∠CFE=90°时,根据相似三角形的性质就可以求出P点的坐标;
②先运用待定系数法求出直线CD的解析式,设P ( http: / / www.21cnjy.com )M与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN就可以表示出三角形PCD的面积,运用顶点式就可以求出结论.
【解答】解:(1)在Rt△AOB中,OA=1,tan∠BAO==3,
∴OB=3OA=3.
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB,
∴OC=OB=3,OD=OA=1,
∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).
代入解析式为
,
解得:.
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)①∵抛物线的解析式为y=﹣x2﹣2x+3,
∴对称轴l=﹣=﹣1,
∴E点的坐标为(﹣1,0).
如图,当∠CEF=90°时,△CEF∽△COD.此时点P在对称轴上,即点P为抛物线的顶点,P(﹣1,4);
当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.
∴,
∴MP=3EM.
∵P的横坐标为t,
∴P(t,﹣t2﹣2t+3).
∵P在第二象限,
∴PM=﹣t2﹣2t+3,EM=﹣1﹣t,
∴﹣t2﹣2t+3=﹣(t﹣1)(t+3),
解得:t1=﹣2,t2=﹣3(因为P与C重合,所以舍去),
∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.
∴P(﹣2,3).
∴当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3);
②设直线CD的解析式为y=kx+b,由题意,得
,
解得:,
∴直线CD的解析式为:y=x+1.
设PM与CD的交点为N,则点N的坐标为(t, t+1),
∴NM=t+1.
∴PN=PM﹣NM=﹣t2﹣2t+3﹣(t+1)=﹣t2﹣+2.
∵S△PCD=S△PCN+S△PDN,
∴S△PCD=PN CM+PN OM
=PN(CM+OM)
=PN OC
=×3(﹣t2﹣+2)
=﹣(t+)2+,
∴当t=﹣时,S△PCD的最大值为.
2016年5月11日
同课章节目录
