7. 4圆锥的侧面展开图 同步练习 (无答案)2024-2025学年九年级下册青岛版数学
文档属性
| 名称 | 7. 4圆锥的侧面展开图 同步练习 (无答案)2024-2025学年九年级下册青岛版数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 69.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览

文档简介
7. 4圆锥的侧面展开图
(1)一个圆锥形零件的母线长为 a,底面半径为 r,求这个圆锥形零件的侧面积和表面积.
(2)已知一个圆锥的侧面展开图是圆心角为 36°的扇形 ,扇形面积为 10 cm2 ,求这个圆锥的表面积.
(3)已知在 △ABC中 , ∠C= 90°,AC= 20 cm ,BC= 15 cm , 以直线 AB为轴把这个直角三角形旋转一周 ,
1
求所得旋转体的表面积.
(1)若圆锥的侧面展开图是一个半径为 3 cm 的半圆 ,则该圆锥的底面半径是( ) .
A.1. 5 cm B.2 cm C.2. 5 cm D.3 cm
(2)如图 7-4-11所示 ,在 △ABC中 , ∠C= 90°,AC>BC. 若以 AC为底面圆半径 、BC
为高的圆锥 的 侧 面 积 为 S1 , 以 BC 为 底 面 圆 半 径 、AC 为 高的 圆 锥 的 侧 面 积 为 S2 , 则( ) .
A.S1 =S2 B.S1 >S2
C.S1基础训练
(1)用半径为 6 cm 的半圆围成一个圆锥的侧面 ,则该圆锥的底面半径等于( ) .
A.3 cm B. cm C.2 cm D. cm
图 7-4-11
(2)用如图 7-4-12所示的扇形纸片制作一个圆锥的侧面 ,要求圆锥的高为 4 cm ,底面周长为 6π cm ,则 该扇形的半径为( ) .
A.3 cm B.5 cm C.6 cm D.8 cm
图 7-4-12 图 7-4-13
(3)如图 7-4-13所示 ,在 ☉O中 ,半径 OA= 4, ∠AOB= 120°,用阴影部分的扇形围成一个锥圆锥 ,该圆 锥底面圆的半径是( ) .
A.1 B. D.2
(4)如图 7-4-14所示 ,小红想用扇形薄纸板制作一个底面半径为 9 cm、高为 12 cm 的圆锥形生 日 帽 ,则 该扇形薄纸板的圆心角为( ) .
A.150° B.180° C.216° D.270°
图 7-4-14 图 7-4-15
(5)如图 7-4-15所示 , 已知在 Rt△ABC中 , ∠ACB= 90°,AC= 4,BC= 3, 以 AB边所在的直线为轴 ,将 △ABC旋转一周 ,则得到的几何体的表面积是( ) .
B.24π C. D.12π
拓展提高
(1)已知一个圆锥的母线长为 5 cm ,侧面展开图如图 7-4-16所示 ,且 ∠AOA1 = 120°. 一只蚂蚁欲从圆 锥底面上的点 A出发 ,沿圆锥侧面爬行一周再回到点 A,则蚂蚁爬行的最短路程长为( ) .
A.8 cm B.5 3 cm C.10cm D.5πcm
图 7-4-16 图 7-4-17
(2)如图 7-4-17所示 ,如果从半径为 5 cm 的圆形纸片上剪去圆周的一个扇形 ,将留下的扇形围成 一
个圆锥(接缝处不重叠) ,那么这个圆锥的高是 cm.
(3)如图 7-4-18所示 ,一个高为 8 cm 的圆锥形零件 ,底面圆的直径为 12 cm ,则该圆锥的侧面积是
.
图 7-4-18 图 7-4-19
(4)一个圆锥形零件的母线长为 4,底面半径为 1,则这个圆锥形零件的表面积是 .
(5)小华为参加毕业晚会演出 ,准备制作一顶圆锥形纸帽 ,如图 7-4-19所示. 纸帽的底面半径为 9 cm,母线长 为 30 cm,制作这个纸帽需要纸板的面积至少为 cm2. (结果保留 π)
(6)如图 7-4-20所示 ,一个圆锥的母线长为 3,底面半径为 1,A是底面圆周上一点 ,从点A 出发绕侧面 一周 ,再回到点 A的最短路线长为 .
图 7-4-20
发散思维
(1)如图 7-4-21所示 ,一个圆锥的底面半径为 10 cm,高为 10 15 cm.
图 7-4-21
①求这个圆锥的表面积 ;
②若一只蚂蚁从底面上一点 A出发 ,绕圆锥一周回到 SA上一点 M 处 ,且 SM= 3AM,求这只蚂蚁所走 的最短距离 .
(2)图 7-4-22a是一把打开的雨伞 ,可近似地看成一个圆锥(见图 7-4-22b) . 伞骨(面料下方能够把面料 撑起来的支架)末端各点所在圆的直径 AC长为 15 dm ,伞骨 AB长为9 dm ,现有一块半径为9 dm的圆形面 料 ,经裁剪可用作伞布 .
①求应裁剪多少平方分米的面料 (精确到 0. 1 dm2 )
②求应剪去扇形纸片的圆心角 .
a b
图 7-4-22
3
(1)一个圆锥形零件的母线长为 a,底面半径为 r,求这个圆锥形零件的侧面积和表面积.
(2)已知一个圆锥的侧面展开图是圆心角为 36°的扇形 ,扇形面积为 10 cm2 ,求这个圆锥的表面积.
(3)已知在 △ABC中 , ∠C= 90°,AC= 20 cm ,BC= 15 cm , 以直线 AB为轴把这个直角三角形旋转一周 ,
1
求所得旋转体的表面积.
(1)若圆锥的侧面展开图是一个半径为 3 cm 的半圆 ,则该圆锥的底面半径是( ) .
A.1. 5 cm B.2 cm C.2. 5 cm D.3 cm
(2)如图 7-4-11所示 ,在 △ABC中 , ∠C= 90°,AC>BC. 若以 AC为底面圆半径 、BC
为高的圆锥 的 侧 面 积 为 S1 , 以 BC 为 底 面 圆 半 径 、AC 为 高的 圆 锥 的 侧 面 积 为 S2 , 则( ) .
A.S1 =S2 B.S1 >S2
C.S1
(1)用半径为 6 cm 的半圆围成一个圆锥的侧面 ,则该圆锥的底面半径等于( ) .
A.3 cm B. cm C.2 cm D. cm
图 7-4-11
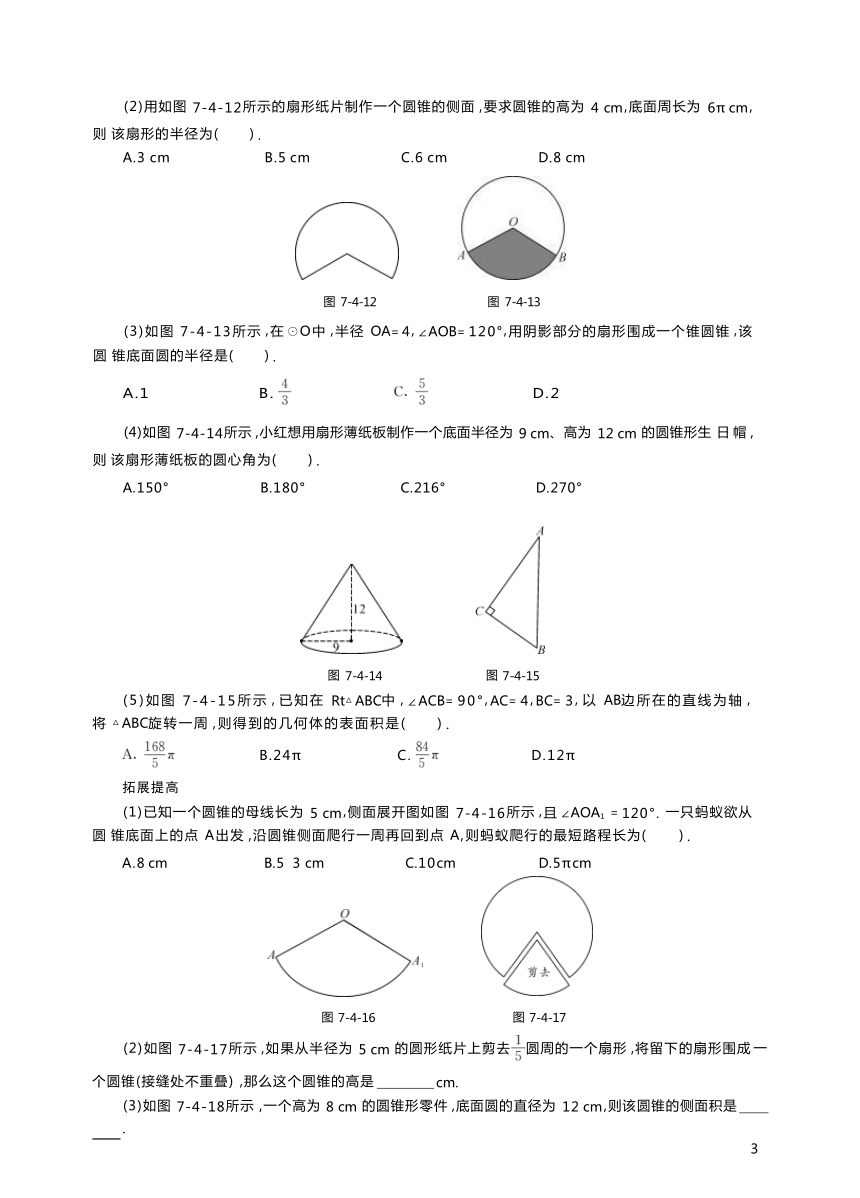
(2)用如图 7-4-12所示的扇形纸片制作一个圆锥的侧面 ,要求圆锥的高为 4 cm ,底面周长为 6π cm ,则 该扇形的半径为( ) .
A.3 cm B.5 cm C.6 cm D.8 cm
图 7-4-12 图 7-4-13
(3)如图 7-4-13所示 ,在 ☉O中 ,半径 OA= 4, ∠AOB= 120°,用阴影部分的扇形围成一个锥圆锥 ,该圆 锥底面圆的半径是( ) .
A.1 B. D.2
(4)如图 7-4-14所示 ,小红想用扇形薄纸板制作一个底面半径为 9 cm、高为 12 cm 的圆锥形生 日 帽 ,则 该扇形薄纸板的圆心角为( ) .
A.150° B.180° C.216° D.270°
图 7-4-14 图 7-4-15
(5)如图 7-4-15所示 , 已知在 Rt△ABC中 , ∠ACB= 90°,AC= 4,BC= 3, 以 AB边所在的直线为轴 ,将 △ABC旋转一周 ,则得到的几何体的表面积是( ) .
B.24π C. D.12π
拓展提高
(1)已知一个圆锥的母线长为 5 cm ,侧面展开图如图 7-4-16所示 ,且 ∠AOA1 = 120°. 一只蚂蚁欲从圆 锥底面上的点 A出发 ,沿圆锥侧面爬行一周再回到点 A,则蚂蚁爬行的最短路程长为( ) .
A.8 cm B.5 3 cm C.10cm D.5πcm
图 7-4-16 图 7-4-17
(2)如图 7-4-17所示 ,如果从半径为 5 cm 的圆形纸片上剪去圆周的一个扇形 ,将留下的扇形围成 一
个圆锥(接缝处不重叠) ,那么这个圆锥的高是 cm.
(3)如图 7-4-18所示 ,一个高为 8 cm 的圆锥形零件 ,底面圆的直径为 12 cm ,则该圆锥的侧面积是
.
图 7-4-18 图 7-4-19
(4)一个圆锥形零件的母线长为 4,底面半径为 1,则这个圆锥形零件的表面积是 .
(5)小华为参加毕业晚会演出 ,准备制作一顶圆锥形纸帽 ,如图 7-4-19所示. 纸帽的底面半径为 9 cm,母线长 为 30 cm,制作这个纸帽需要纸板的面积至少为 cm2. (结果保留 π)
(6)如图 7-4-20所示 ,一个圆锥的母线长为 3,底面半径为 1,A是底面圆周上一点 ,从点A 出发绕侧面 一周 ,再回到点 A的最短路线长为 .
图 7-4-20
发散思维
(1)如图 7-4-21所示 ,一个圆锥的底面半径为 10 cm,高为 10 15 cm.
图 7-4-21
①求这个圆锥的表面积 ;
②若一只蚂蚁从底面上一点 A出发 ,绕圆锥一周回到 SA上一点 M 处 ,且 SM= 3AM,求这只蚂蚁所走 的最短距离 .
(2)图 7-4-22a是一把打开的雨伞 ,可近似地看成一个圆锥(见图 7-4-22b) . 伞骨(面料下方能够把面料 撑起来的支架)末端各点所在圆的直径 AC长为 15 dm ,伞骨 AB长为9 dm ,现有一块半径为9 dm的圆形面 料 ,经裁剪可用作伞布 .
①求应裁剪多少平方分米的面料 (精确到 0. 1 dm2 )
②求应剪去扇形纸片的圆心角 .
a b
图 7-4-22
3
