17.1勾股定理 培优练习(含答案) 人教版2024—2025学年八年级下册
文档属性
| 名称 | 17.1勾股定理 培优练习(含答案) 人教版2024—2025学年八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 288.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 20:24:49 | ||
图片预览



文档简介
17.1勾股定理培优练习人教版2024—2025学年八年级下册
一、知识点梳理:
1、勾股定理:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方。
(1)在直角三角形中,若已知任意两边,就可以运用勾股定理求出第三边.无直角时,可作垂线构造直角三角形.
变式:
(2)勾股定理的作用:(1)计算;(2)证明带有平方的问题;(3)实际应用.
(3)利用勾股定理可以画出长度是无理数的线段,也就可以在数轴上画出表示无理数的点.
考点一、勾股数
例1、下列各组数中,是勾股数的一组是( )
A.0.3,0.4,0.5 B.
C.4,5,6 D.6,8,10
变式1、下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
变式2、如图所示,正方形的边长为1,则数轴上的点P表示的实数为 .
考点二、勾股定理中的面积问题
例2、如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形ABC中,AC=17,BC=15,则阴影部分的面积是 .
变式1、如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=16.则S3=( )
A.20 B.12
C.2 D.2
变式2、如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
考点三、勾股定理中的赵爽弦图
例3、中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.下图是3世纪我国汉代的数学家赵爽在注解《周髀算经》时给出的图案,人们称它为“赵爽弦图”.此图中四个全等的直角三角形可以围成一个大正方形,中空的部分是一个小正方形.如果大正方形的面积是25,小正方形的面积是1,则(a+b)2的值是 .
变式1、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果大正方形的边长是5,小正方形的边长是2,直角三角形的两直角边长分别是a,b(b>a),则(a+b)2的值为( )
A.16 B.23 C.35.5 D.46
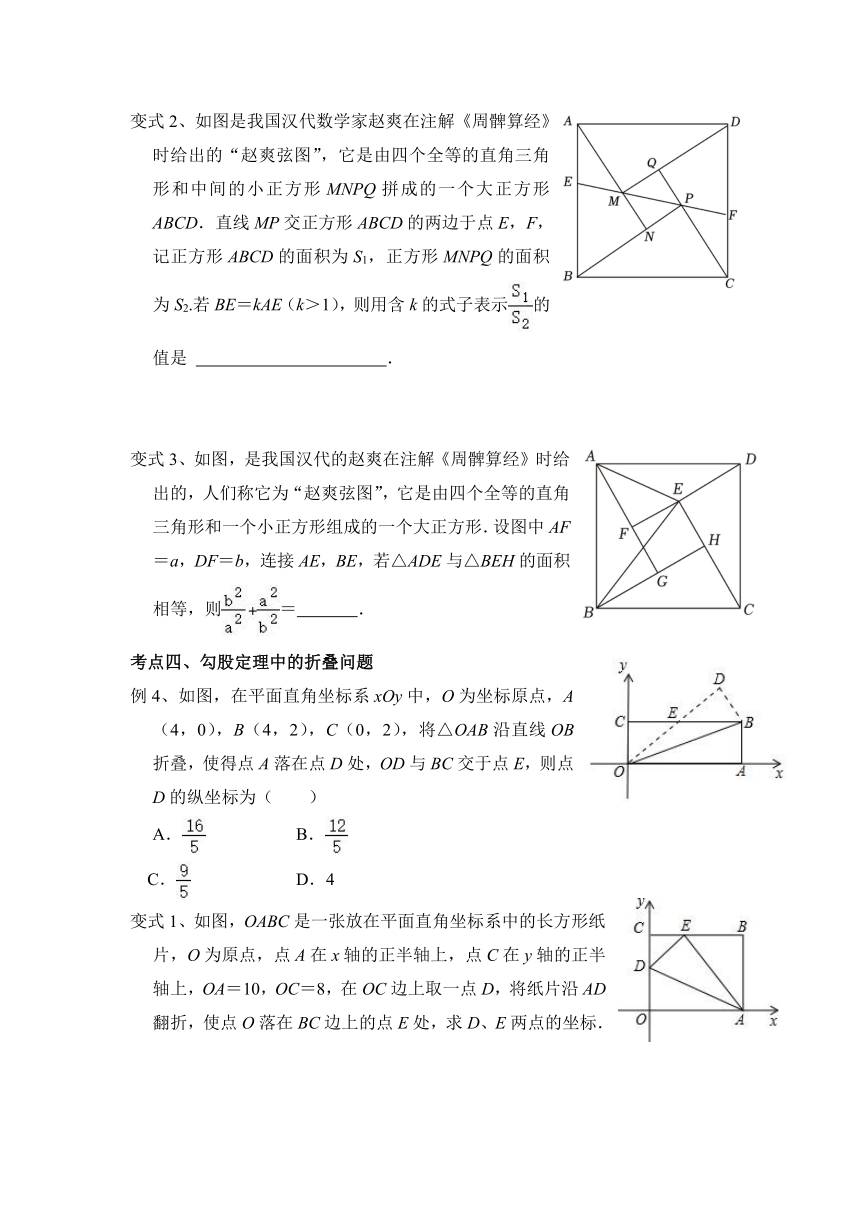
变式2、如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ拼成的一个大正方形ABCD.直线MP交正方形ABCD的两边于点E,F,记正方形ABCD的面积为S1,正方形MNPQ的面积为S2.若BE=kAE(k>1),则用含k的式子表示的值是 .
变式3、如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b,连接AE,BE,若△ADE与△BEH的面积相等,则= .
考点四、勾股定理中的折叠问题
例4、如图,在平面直角坐标系xOy中,O为坐标原点,A(4,0),B(4,2),C(0,2),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则点D的纵坐标为( )
B.
C. D.4
变式1、如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
变式2、如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,CD′交AB于点F,求重叠部分△AFC的面积.
变式3、如图所示,在 ABC中,AB=20,AC=12,BC=16,把 ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.
变式4、如图,将边长为8 cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在点F处,折痕为MN,求线段CN的长.
变式5、有一边长为2的正方形纸片ABCD,先将正方形ABCD对折,设折痕为EF;再沿过点D的折痕将角A翻折,使得点A落在EF的H上,折痕交AE于点G,求EG的长。
变式6、如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合,若长方形的长BC为8,宽AB为4,求:
(1)DE的长;
(2)求阴影部分△GED的面积.
考点五、勾股定理中在生活中的应用
例5、如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
变式1、拖拉机行驶过程中会对周围产生较大的噪声影响.如图.有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,拖拉机周围130m以内为受噪声影响区域.
(1)求∠ACB度数;
(2)学校C会受噪声影响吗?为什么?
(3)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
变式2、如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.
变式3、我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?
考点六、勾股定理中的最短路径问题
例6、如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
变式1、如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A.13cm B.2cm C.cm D.2cm
变式2、如图,一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为( )
a B.(1+)a
C.3a D.a
变式3、如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.5 B.25
C.10+5 D.35
考点七、勾股定理中的综合应用
例7、如图,在Rt△ABC中,已知∠A=90°,D是斜边BC的中点,DE⊥BC交AB于点E,连接CE.
(1)求证:BE2﹣AE2=AC2;
(2)若AC=6,BD=5,求△ACE的周长.
变式1、一直角三角形的两边长分别为3和4,则第三边长为( )
A.5 B.5或
C. D.以上都不对
变式2、如图,在Rt△ABC中,∠A=90°,D是斜边BC的中点,DE⊥DF,
求证:EF2=BE2+CF2
变式3、如图,已知△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5,求△DEF的面积。
一、知识点梳理:
1、勾股定理:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方。
(1)在直角三角形中,若已知任意两边,就可以运用勾股定理求出第三边.无直角时,可作垂线构造直角三角形.
变式:
(2)勾股定理的作用:(1)计算;(2)证明带有平方的问题;(3)实际应用.
(3)利用勾股定理可以画出长度是无理数的线段,也就可以在数轴上画出表示无理数的点.
考点一、勾股数
例1、下列各组数中,是勾股数的一组是( )
A.0.3,0.4,0.5 B.
C.4,5,6 D.6,8,10
变式1、下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
变式2、如图所示,正方形的边长为1,则数轴上的点P表示的实数为 .
考点二、勾股定理中的面积问题
例2、如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形ABC中,AC=17,BC=15,则阴影部分的面积是 .
变式1、如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=16.则S3=( )
A.20 B.12
C.2 D.2
变式2、如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
考点三、勾股定理中的赵爽弦图
例3、中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.下图是3世纪我国汉代的数学家赵爽在注解《周髀算经》时给出的图案,人们称它为“赵爽弦图”.此图中四个全等的直角三角形可以围成一个大正方形,中空的部分是一个小正方形.如果大正方形的面积是25,小正方形的面积是1,则(a+b)2的值是 .
变式1、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果大正方形的边长是5,小正方形的边长是2,直角三角形的两直角边长分别是a,b(b>a),则(a+b)2的值为( )
A.16 B.23 C.35.5 D.46
变式2、如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ拼成的一个大正方形ABCD.直线MP交正方形ABCD的两边于点E,F,记正方形ABCD的面积为S1,正方形MNPQ的面积为S2.若BE=kAE(k>1),则用含k的式子表示的值是 .
变式3、如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b,连接AE,BE,若△ADE与△BEH的面积相等,则= .
考点四、勾股定理中的折叠问题
例4、如图,在平面直角坐标系xOy中,O为坐标原点,A(4,0),B(4,2),C(0,2),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则点D的纵坐标为( )
B.
C. D.4
变式1、如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
变式2、如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,CD′交AB于点F,求重叠部分△AFC的面积.
变式3、如图所示,在 ABC中,AB=20,AC=12,BC=16,把 ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.
变式4、如图,将边长为8 cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在点F处,折痕为MN,求线段CN的长.
变式5、有一边长为2的正方形纸片ABCD,先将正方形ABCD对折,设折痕为EF;再沿过点D的折痕将角A翻折,使得点A落在EF的H上,折痕交AE于点G,求EG的长。
变式6、如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合,若长方形的长BC为8,宽AB为4,求:
(1)DE的长;
(2)求阴影部分△GED的面积.
考点五、勾股定理中在生活中的应用
例5、如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
变式1、拖拉机行驶过程中会对周围产生较大的噪声影响.如图.有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,拖拉机周围130m以内为受噪声影响区域.
(1)求∠ACB度数;
(2)学校C会受噪声影响吗?为什么?
(3)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
变式2、如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.
变式3、我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?
考点六、勾股定理中的最短路径问题
例6、如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
变式1、如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A.13cm B.2cm C.cm D.2cm
变式2、如图,一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为( )
a B.(1+)a
C.3a D.a
变式3、如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.5 B.25
C.10+5 D.35
考点七、勾股定理中的综合应用
例7、如图,在Rt△ABC中,已知∠A=90°,D是斜边BC的中点,DE⊥BC交AB于点E,连接CE.
(1)求证:BE2﹣AE2=AC2;
(2)若AC=6,BD=5,求△ACE的周长.
变式1、一直角三角形的两边长分别为3和4,则第三边长为( )
A.5 B.5或
C. D.以上都不对
变式2、如图,在Rt△ABC中,∠A=90°,D是斜边BC的中点,DE⊥DF,
求证:EF2=BE2+CF2
变式3、如图,已知△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5,求△DEF的面积。
