直线和圆的位置关系

课件24张PPT。直线与圆的位置关系【学习目标】1、掌握直线与圆的位置关系，能用数量来判断直线与圆的位置关系.
2、在学习中领会类比和分类等数学思想.观察直线和圆的位置关系观察直线和圆的位置关系探究目的：探究直线和圆有几种位置关系
活动方式：
1.动手操作：作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,仔细观察，直线和圆的交点个数如何变化？
2.动脑思考：
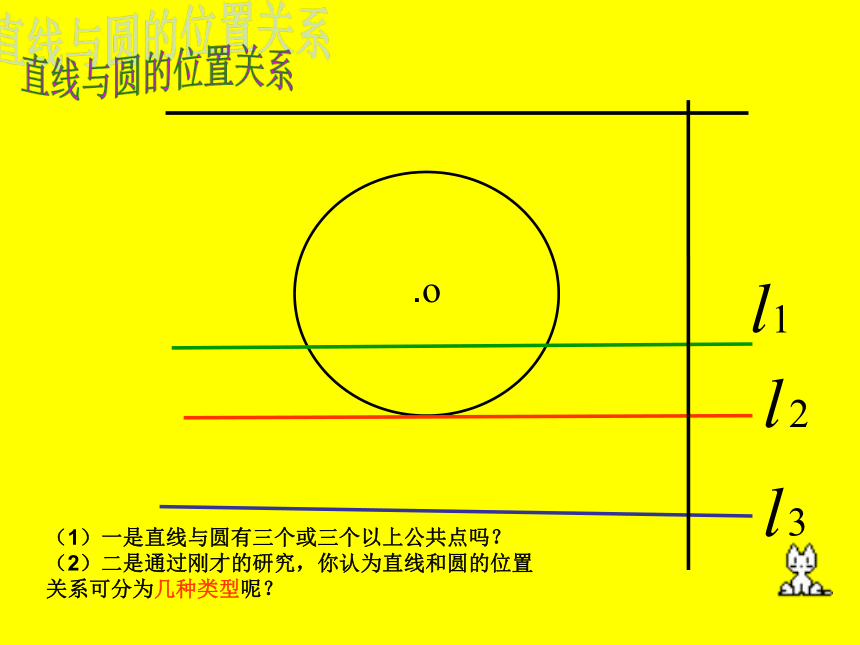
（1）一是直线与圆有三个或三个以上公共点吗？
（2）二是通过刚才的研究，你认为直线和圆的位置关系可分为几种类型呢？我们一起来探究直线与圆的位置关系.o（1）一是直线与圆有三个或三个以上公共点吗？
（2）二是通过刚才的研究，你认为直线和圆的位置关系可分为几种类型呢？
.O特点：.O叫做直线和圆相离.直线和圆没有公共点，特点：直线和圆有唯一的公共点，叫做直线和圆相切.这时的直线叫切线，
唯一的公共点叫切点..O特点：直线和圆有两个公共点，叫直线和圆相交，这时的直线叫做圆的割线.1、直线与圆的位置关系(图形特征----用公共点的个数来区分）.A.A.B切点我们一起来归纳
我们可以根据直线与圆的公共点的个数 来判断直线与圆的位置关系.
小小体会用数学的眼光看生活用数学的眼光看生活用数学的眼光看生活１、直线与圆最多有两个公共点 . （　） √×3 、若A是⊙O上一点， 则直线AB与⊙O相切 .( ).A.O２、若直线与圆相交，则直线上的点都在圆内.( ) 4 、若C为⊙O外的一点，则过点C的直线CD与
⊙O 相交或相离. （ ）××.C我们一起来判断1、看图判断直线l与 ⊙O的位置关系（1）（2）（3）（4）（5）相离相切相交相交？lllll·O·O·O·O·O我们一起来观察（5）？l 如果公共点的个数不好判断，该怎么办？·O “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析？·
A·
B如图.O为直线L外一点,OT⊥L,且OT=d.请以
O为圆心,分别以 为半径画圆.
所画的圆与直线l有什么位置关系?
-----做一做我们一起来探究（2）dr相离Adr相切H1、直线与圆相离 d>r2、直线与圆相切 d=r3 、直线与圆相交 dC.OB直线与圆的位置关系的判定与性质.
E. FO0d>r1d=r切点切线2d为7cm，则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.零相离一个小结:利用圆心到直线的距离与半径的大小关
系来判定直线与圆的位置关系(1)、已知⊙O的半径是5.5cm ，点O到直线a的距离
是5.5cm，则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.(3)、直线m上一点A到圆心O的距离等于⊙O的半径，
则直线m与⊙O的位置关系是 .相切 或相交我们一起来练习 在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆
与AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm (3)r=3cm.BCAD4532.4cm我们一起来提高即圆心C到AB的距离d=2.4cm。（1）当r=2cm时， ∵d＞r，
∴⊙C与AB相离.（2）当r=2.4cm时，∵d=r，
∴⊙C与AB相切.（3）当r=3cm时， ∵d＜r，
∴⊙C与AB相交.解：过C作CD⊥AB，垂足为D.在Rt△ABC中，AB= ==5（cm）根据三角形面积公式有CD·AB=AC·BC∴CD= =2222=2.4（cm）.例: Rt△ABC,∠C=90°AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm
(3)r=3cm.在Rt△ABC中，∠C=90°，
AC=3cm，BC=4cm，
以C为圆心，r为半径作圆。想一想? 当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm数学日记
课题 日期
今天的课堂中，探索了___________________,
学会了________________________________,
这节课堂上我最满意的是__________________,
我仍困惑的是____________________________.成长=
经验+反思。 我们一起来反思
拓展作业：在Rt△ABC 中，∠C=Rt∠，AC=8cm，BC=6cm，若要以C为圆心，R为半径画圆，请根据下列条件，求半径R的值或取值范围
1、AB与圆相离?? 2、AB与圆相交?? 3、AB与圆相切快乐探究到课下