5.2第 3 课时反比例函数(3)(同步练习)(无答案)2024-2025学年九年级下册青岛版数学
文档属性
| 名称 | 5.2第 3 课时反比例函数(3)(同步练习)(无答案)2024-2025学年九年级下册青岛版数学 |  | |
| 格式 | docx | ||
| 文件大小 | 83.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 09:24:19 | ||
图片预览

文档简介
第 3 课时反比例函数(3)
(1)若函数 的图像经过(3, -4) ,则 k= . 此图像位于第 象限 . 在每个象限内 ,y
随 x 的减小而 .
(2)在 △ABC的三个顶点 A(2, -3) ,B( -4, -5) ,C( -3,2)中 ,可能在反比例函数 的图像
上的点是 .
1
(1)两个反比例函数和 在第一象限内的图像如图 5-2-29所示 ,点 P 在的图像上 ,PC⊥x轴于点C,交y= 的图像于点 A,PD⊥y轴于点 D,交 y= 的图像于点B. 当点P在 y= 的图像上运动时 ,有如下结论:①△ODB与 △OCA
的面积相等 ;②四边形 PAOB的面积不会发生变化 ;③PA与 PB 始终相等 ;④当点 A
是 PC的中点时 ,点 B一定是 PD的中点. 其中一定正确的是 . (填序号)
(2)如图 5-2-30所示 ,在直角坐标系中 ,点 O为坐标系原点 ,矩形 OABC的边
OA,OC分别在 x 轴和 y 轴上 ,其中 OA= 6,OC= 3. 已知反比例函数
的图像经过 BC边上的中点 D ,交 AB于点 E.
①k的值为 ;
②猜想 △OCD的面积与 △OBE的面积之间的关系 ,请说明理由 .
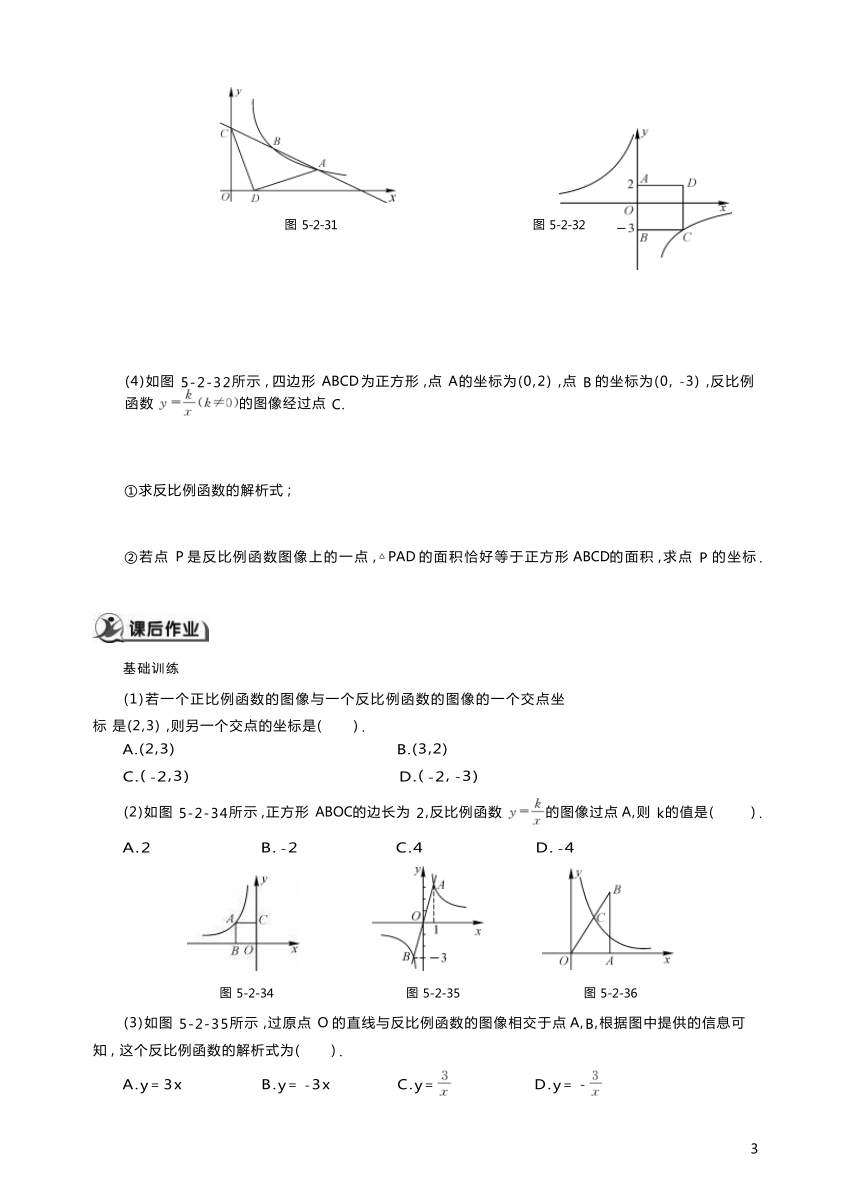
(3)如图 5-2-31所示 , 已知反比例函数 与一次函数y=kx+b的图像相
交于A(4,1) ,B(a,2)两点 ,一次函数的图像与 y轴的交点为 C.
①求反比例函数和一次函数的解析式 ;
②若点 D 的坐标为(1,0) ,求 △ACD的面积.
图 5-2-29
图 5-2-30
图 5-2-31 图 5-2-32
(4)如图 5-2-32所示 , 四边形 ABCD 为正方形 ,点 A的坐标为(0,2) ,点 B 的坐标为(0, -3) ,反比例函数 的图像经过点 C.
①求反比例函数的解析式 ;
②若点 P 是反比例函数图像上的一点 ,△PAD 的面积恰好等于正方形 ABCD的面积 ,求点 P 的坐标 .
基础训练
(1)若一个正比例函数的图像与一个反比例函数的图像的一个交点坐标 是(2,3) ,则另一个交点的坐标是( ) .
A.(2,3) B.(3,2)
C.( -2,3) D.( -2, -3)
(2)如图 5-2-34所示 ,正方形 ABOC的边长为 2,反比例函数 的图像过点 A,则 k的值是( ) .
A.2 B. -2 C.4 D. -4
图 5-2-34 图 5-2-35 图 5-2-36
(3)如图 5-2-35所示 ,过原点 O 的直线与反比例函数的图像相交于点 A,B,根据图中提供的信息可知 , 这个反比例函数的解析式为( ) .
A.y= 3x B.y= -3x C.y= D.y= -
(4)两位同学在描述同一反比例函数的图像时 , 甲同学说:“从这个反比例函数图像上任意一点向 x轴、y轴 作垂线 ,与两坐标轴所围成的矩形面积为 2014”.乙同学说:“这个反比例函数图像与直线 y= -x有两个交点. ” 你认为这两位同学所描述的反比例函数的解析式是 .
(5)如果反比例函数 的图像经过点(2,1)与( -1,n) ,那么 n 的值为 .
(6)如图 5-2-36所示 ,在直角坐标系中 ,点 A 在 x 轴上 ,OA= 3,AB= 4,OA⊥AB.
①△OAB的面积为 .
②若点C在线段 OB上 ,OC= 2BC,双曲线 过点 C,则 k= .
拓展提高
(1)如图 5-2-37所示 , 已知正方形 OABC的面积是 9,点 O 为坐标原点 ,点 B 是反比例函数
0,x>0)的图像上的点 .
①求点 B 的坐标与 k 的值 ;
②若点 P 也是函数图像上的一点 ,过点 P 作 x 轴的垂线 ,垂足为 E,连接 PA. 当 △PEA的面积等于 3 时 ,求点 P 的坐标 .
图 5-2-37
(2)如右图所示 ,在直角坐标系中 ,边长为 2 的正方形ABCD 关于 y 轴
对称 ,边 AD 在 x 轴上 ,点 B在第四象限 ,直线 BD 与反比例函数的图像交
于点 B,E.
①求反比例函数及直线 BD 的解析式 ;
②求点 E 的坐标 .
发散思维
3
(1)已知反比例函数 和一次函数 y=x-6.
①若一次函数与反比例函数的图像交于点 P(2,m) ,求 m 和k的值.
②当 k满足什么条件时 ,两函数的图像没有交点
(2)如图 5-2-39所示 ,A,B两点在函数的图像上 .
①求 k的值及直线 AB的解析式 ;
②如果一个点的横 、纵坐标均为整数 ,那么我们称这个点是格点 . 请直接写出图 中直线 AB与双曲线所围部分(不包括边界)含有格点的个数 .
图 5-2-39
(1)若函数 的图像经过(3, -4) ,则 k= . 此图像位于第 象限 . 在每个象限内 ,y
随 x 的减小而 .
(2)在 △ABC的三个顶点 A(2, -3) ,B( -4, -5) ,C( -3,2)中 ,可能在反比例函数 的图像
上的点是 .
1
(1)两个反比例函数和 在第一象限内的图像如图 5-2-29所示 ,点 P 在的图像上 ,PC⊥x轴于点C,交y= 的图像于点 A,PD⊥y轴于点 D,交 y= 的图像于点B. 当点P在 y= 的图像上运动时 ,有如下结论:①△ODB与 △OCA
的面积相等 ;②四边形 PAOB的面积不会发生变化 ;③PA与 PB 始终相等 ;④当点 A
是 PC的中点时 ,点 B一定是 PD的中点. 其中一定正确的是 . (填序号)
(2)如图 5-2-30所示 ,在直角坐标系中 ,点 O为坐标系原点 ,矩形 OABC的边
OA,OC分别在 x 轴和 y 轴上 ,其中 OA= 6,OC= 3. 已知反比例函数
的图像经过 BC边上的中点 D ,交 AB于点 E.
①k的值为 ;
②猜想 △OCD的面积与 △OBE的面积之间的关系 ,请说明理由 .
(3)如图 5-2-31所示 , 已知反比例函数 与一次函数y=kx+b的图像相
交于A(4,1) ,B(a,2)两点 ,一次函数的图像与 y轴的交点为 C.
①求反比例函数和一次函数的解析式 ;
②若点 D 的坐标为(1,0) ,求 △ACD的面积.
图 5-2-29
图 5-2-30
图 5-2-31 图 5-2-32
(4)如图 5-2-32所示 , 四边形 ABCD 为正方形 ,点 A的坐标为(0,2) ,点 B 的坐标为(0, -3) ,反比例函数 的图像经过点 C.
①求反比例函数的解析式 ;
②若点 P 是反比例函数图像上的一点 ,△PAD 的面积恰好等于正方形 ABCD的面积 ,求点 P 的坐标 .
基础训练
(1)若一个正比例函数的图像与一个反比例函数的图像的一个交点坐标 是(2,3) ,则另一个交点的坐标是( ) .
A.(2,3) B.(3,2)
C.( -2,3) D.( -2, -3)
(2)如图 5-2-34所示 ,正方形 ABOC的边长为 2,反比例函数 的图像过点 A,则 k的值是( ) .
A.2 B. -2 C.4 D. -4
图 5-2-34 图 5-2-35 图 5-2-36
(3)如图 5-2-35所示 ,过原点 O 的直线与反比例函数的图像相交于点 A,B,根据图中提供的信息可知 , 这个反比例函数的解析式为( ) .
A.y= 3x B.y= -3x C.y= D.y= -
(4)两位同学在描述同一反比例函数的图像时 , 甲同学说:“从这个反比例函数图像上任意一点向 x轴、y轴 作垂线 ,与两坐标轴所围成的矩形面积为 2014”.乙同学说:“这个反比例函数图像与直线 y= -x有两个交点. ” 你认为这两位同学所描述的反比例函数的解析式是 .
(5)如果反比例函数 的图像经过点(2,1)与( -1,n) ,那么 n 的值为 .
(6)如图 5-2-36所示 ,在直角坐标系中 ,点 A 在 x 轴上 ,OA= 3,AB= 4,OA⊥AB.
①△OAB的面积为 .
②若点C在线段 OB上 ,OC= 2BC,双曲线 过点 C,则 k= .
拓展提高
(1)如图 5-2-37所示 , 已知正方形 OABC的面积是 9,点 O 为坐标原点 ,点 B 是反比例函数
0,x>0)的图像上的点 .
①求点 B 的坐标与 k 的值 ;
②若点 P 也是函数图像上的一点 ,过点 P 作 x 轴的垂线 ,垂足为 E,连接 PA. 当 △PEA的面积等于 3 时 ,求点 P 的坐标 .
图 5-2-37
(2)如右图所示 ,在直角坐标系中 ,边长为 2 的正方形ABCD 关于 y 轴
对称 ,边 AD 在 x 轴上 ,点 B在第四象限 ,直线 BD 与反比例函数的图像交
于点 B,E.
①求反比例函数及直线 BD 的解析式 ;
②求点 E 的坐标 .
发散思维
3
(1)已知反比例函数 和一次函数 y=x-6.
①若一次函数与反比例函数的图像交于点 P(2,m) ,求 m 和k的值.
②当 k满足什么条件时 ,两函数的图像没有交点
(2)如图 5-2-39所示 ,A,B两点在函数的图像上 .
①求 k的值及直线 AB的解析式 ;
②如果一个点的横 、纵坐标均为整数 ,那么我们称这个点是格点 . 请直接写出图 中直线 AB与双曲线所围部分(不包括边界)含有格点的个数 .
图 5-2-39
