2024-2025学年浙教版七年级数学下册期中真题专项复习02单项选择(含答案)(浙江专用)
文档属性
| 名称 | 2024-2025学年浙教版七年级数学下册期中真题专项复习02单项选择(含答案)(浙江专用) |  | |
| 格式 | docx | ||
| 文件大小 | 346.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 21:31:41 | ||
图片预览



文档简介
2024-2025学年七年级数学下册期中真题专项复习02单项选择
1.(2024七下·杭州期中)如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
2.(2024七下·浦江期中)若分式的值为零, 则x 的值为( )
A.x = 2 B.x = -2
C.x = 2或x= -2 D.x = 3
3.(2024七下·浦江期中)某种生物细胞的直径是0.000000012cm,用科学记数法表示,正确的是 ( )
A.12 ×10-7 cm B.1.2 ×10-7 cm
C.12 ×10-8 cm D.1.2 ×10-8 cm
4.(2024七下·温州期中) 石墨烯理论厚度是,数据用科学记数法表示为( )
A. B. C. D.
5.(2024七下·开化期中)下列是二元一次方程的是( )
A. B. C. D.
6.(2024·七下婺城期中)下列方程是二元一次方程的是( )
A. B. C. D.
7.(2024·七下婺城期中) 设a,b是实数,定义一种新运算:.下面有四个推断:
①,②,③,④.
其中推断正确的是( )
A.①②③④ B.①③④ C.①② D.①③
8.(2024七下·浦江期中)下列多项式不能用平方差公式因式分解的是( )
A.-m2+4 B.-x2-y2
C.x2y2-1 D.(m-a)2-(m+a)2
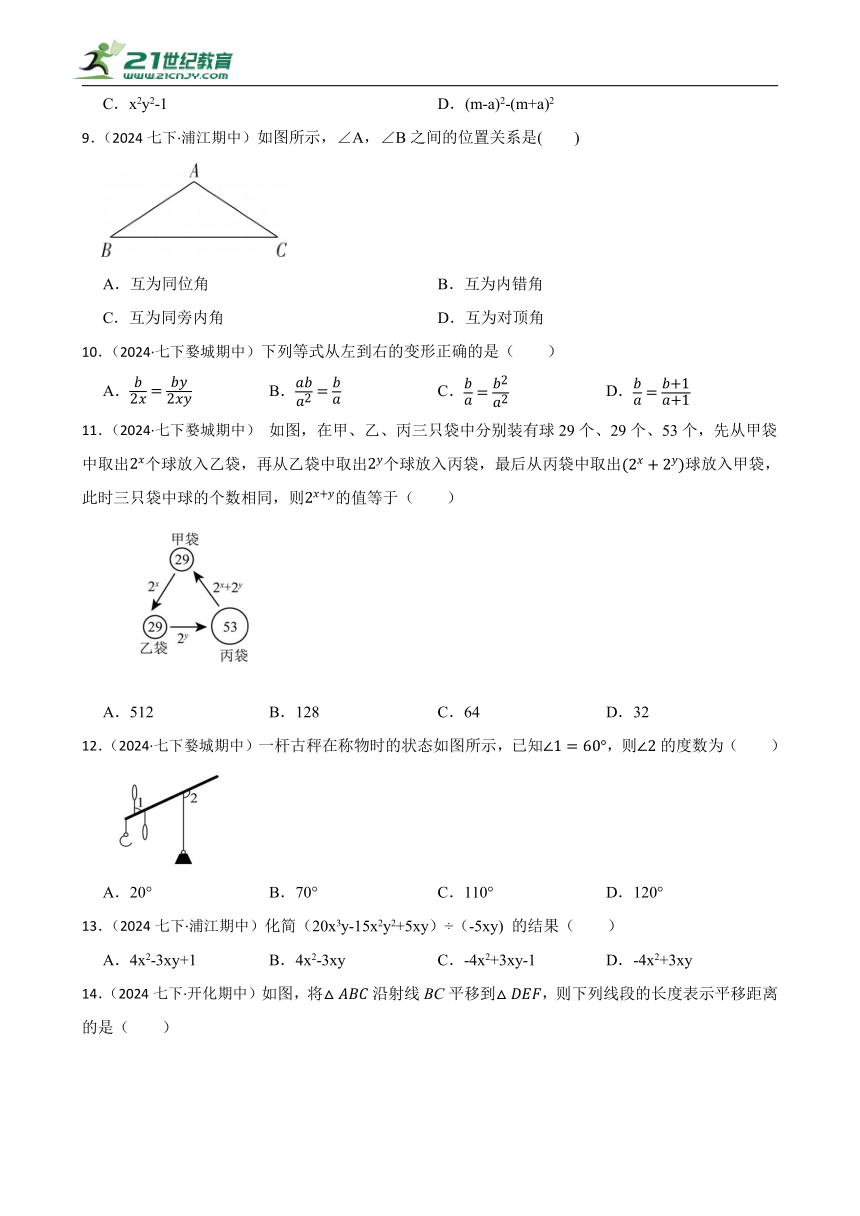
9.(2024七下·浦江期中)如图所示,∠A,∠B之间的位置关系是( )
A.互为同位角 B.互为内错角
C.互为同旁内角 D.互为对顶角
10.(2024·七下婺城期中)下列等式从左到右的变形正确的是( )
A. B. C. D.
11.(2024·七下婺城期中) 如图,在甲、乙、丙三只袋中分别装有球29个、29个、53个,先从甲袋中取出个球放入乙袋,再从乙袋中取出个球放入丙袋,最后从丙袋中取出球放入甲袋,此时三只袋中球的个数相同,则的值等于( )
A.512 B.128 C.64 D.32
12.(2024·七下婺城期中)一杆古秤在称物时的状态如图所示,已知,则的度数为( )
A.20° B.70° C.110° D.120°
13.(2024七下·浦江期中)化简(20x3y-15x2y2+5xy)÷(-5xy) 的结果( )
A.4x2-3xy+1 B.4x2-3xy C.-4x2+3xy-1 D.-4x2+3xy
14.(2024七下·开化期中)如图,将沿射线BC平移到,则下列线段的长度表示平移距离的是( )
A.BC B.BF C.BE D.CE
15.(2024七下·浦江期中)下列计算正确的是 ( )
A. B. C. D.
16.(2024七下·开化期中)如图,在所标识的角中,内错角是( )
A.和 B.和 C.和 D.和
17.(2024七下·杭州期中)下列运算正确的是( )
A. B. C. D.
18.(2024七下·浦江期中)数学兴趣小组同学利用几何图形画出螳螂的简笔画如图所示,已知∠BAC=128°,且∠CDE=70°,则∠ACD=( )
A.18° B.58° C.48° D.38 °
19.(2024·七下婺城期中)小时候我们用肥皂水吹泡泡,泡沫的厚度约为0.000326毫米,将数据0.000326用科学记数法表示为( )
A. B.
C. D.
20.(2024·七下婺城期中)下列计算正确的是( )
A. B. C. D.
21.(2024七下·邵阳期末)已知m,n是整数,且mn-2n+3m-9=0,则mn的值有( )个
A.1个 B.2个 C.3个 D.4个
22.(2024七下·开化期中)可以表示为( )
A. B. C. D.
23.(2024七下·温州期中) 已知二元一次方程组,则的值是( )
A.9 B.3 C. D.
24.(2024七下·西湖期中) 如果,那么的值分别是( )
A. B.
C. D.
25.(2024七下·杭州期中) 我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B.
C. D.
26.(2024七下·温州期中) 如图,将正方形与正方形叠在一起,且这两个正方形的边长之差为,两个正方形相交于点M、N,连结,,若阴影部分的面积是9,,,则正方形的边长为( )
A. B.4 C.4.2 D.4.5
27.(2024七下·杭州期中)下列图形中,∠1与∠2是内错角的是( )
A. B.
C. D.
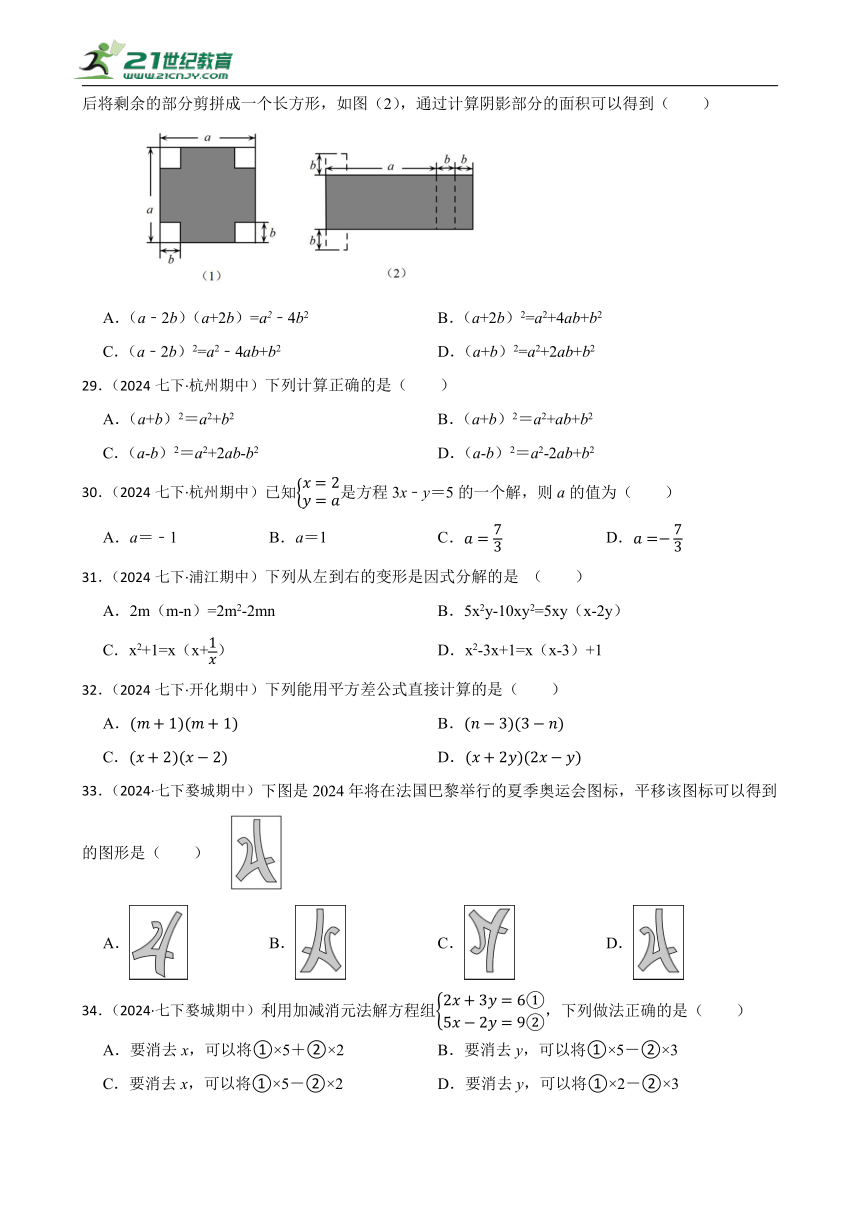
28.(2024·七下婺城期中)如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( )
A.(a﹣2b)(a+2b)=a2﹣4b2 B.(a+2b)2=a2+4ab+b2
C.(a﹣2b)2=a2﹣4ab+b2 D.(a+b)2=a2+2ab+b2
29.(2024七下·杭州期中)下列计算正确的是( )
A.(a+b)2=a2+b2 B.(a+b)2=a2+ab+b2
C.(a-b)2=a2+2ab-b2 D.(a-b)2=a2-2ab+b2
30.(2024七下·杭州期中)已知是方程3x﹣y=5的一个解,则a的值为( )
A.a=﹣1 B.a=1 C. D.
31.(2024七下·浦江期中)下列从左到右的变形是因式分解的是 ( )
A.2m(m-n)=2m2-2mn B.5x2y-10xy2=5xy(x-2y)
C.x2+1=x(x+) D.x2-3x+1=x(x-3)+1
32.(2024七下·开化期中)下列能用平方差公式直接计算的是( )
A. B.
C. D.
33.(2024·七下婺城期中)下图是2024年将在法国巴黎举行的夏季奥运会图标,平移该图标可以得到的图形是( )
A. B. C. D.
34.(2024·七下婺城期中)利用加减消元法解方程组,下列做法正确的是( )
A.要消去x,可以将①×5+②×2 B.要消去y,可以将①×5-②×3
C.要消去x,可以将①×5-②×2 D.要消去y,可以将①×2-②×3
35.(2024七下·温州期中) 如图,一块直尺与一个直角三角形如图放置,若,则的度数为( )
A. B. C. D.
36.(2024七下·温州期中) 一个正方形的边长增加,面积相应增加,则这个正方形的边长为( )
A.8 B.5 C.6 D.7
37.(2024七下·杭州期中)下列各式中,能用平方差公式计算的是( )
A.(3x+5y)(5y﹣3x) B.(m﹣n)(n﹣m)
C.(p+q)(﹣p﹣q) D.(2a+3b)(3a﹣2b)
38.(2024七下·开化期中)如图,将一块三角板中含有60°角的顶点放在直尺的一边上,若,那么的度数为( )
A.80° B.70° C.40° D.30°
39.(2024七下·永寿期中)的运算结果为( )
A. B. C. D.
40.(2024七下·杭州期中)若方程组的解也是方程3x+ky=10的解,则k的值是( )
A. B. C. D.
41.(2024七下·浦江期中)代数式4x2+3mx+9能写成一个整式的完全平方的形式,则 m= ( )
A.12 B.±12 C.4 D.±4
42.(2024七下·杭州期中)已知a,b是常数,若化简(x+a)(2x2+bx3)的结果不含x的二次项,则36a﹣18b﹣1的值为( )
A.﹣1 B.0 C.17 D.35
43.(2024七下·开化期中)下列说法错误的是( )
A.经过直线外一点,有且只有一条直线与已知直线平行.
B.在同一平面内,垂直于同一条直线的两条直线互相平行.
C.两条直线被第三条直线所截,截得的同位角相等.
D.在同一个平面内,不相交的两条直线是平行线.
44.(2024七下·温州期中) 下列图形中,与是同位角的是( )
A. B.
C. D.
45.(2024七下·开化期中)《九章算术》中记载了一道有趣的数学问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱,问人数、物价各多少?”设人数为x人,物价为y钱,根据题意,可列方程组( )
A. B.
C. D.
46.(2024七下·杭州期中)设“●、▲、■”分别表示三种不同的物体.如图所示,前两架天平保持平衡,如果要使第三架天平也保持平衡,那么“?”处应放“■”的个数为( )
A.5 B.4 C.3 D.2
47.(2024七下·开化期中)若代数式,则的值是( )
A. B.0 C.1 D.2
48.(2024七下·杭州期中)如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
49.(2024七下·温州期中) 下列各式是二元一次方程的是( )
A. B.
C. D.
50.(2024七下·开化期中)图1是一种长为a宽为b的长方形,将这样四个形状和大小完全相同的长方形摆放在一个长为5宽为4的大长方形中,如图2所示,则图2中阴影部分面积是( )
A.8 B.12 C.15 D.16
答案解析部分
1.C
解:由平移的性质可知:AD=BE=CF=1,
∵EC=2,
∴BF=BE+CE+CF=1+2+1=4,
故答案为:C.
根据平移的性质可知:AD=BE=CF=1,将代入求解即可。
2.B
解:∵ 分式的值为零,
∴x-2≠0,且x2-4=0,
解得:x=﹣2.
故答案为:B.
当分式满足,A=0且B≠0.
3.D
解:0.000000012=1.2×10-8.
故答案为:D.
大于0小于1的数用科学记数法表示为a×10-n,其中1≤a<10,n为原数字从左往右数第一个不为0的数字前面的0的个数.
4.A
解:,
故答案为:A.
用科学记数法表示绝对值小于1的数,用科学记数法表示为,其中,的值为第一个不为0的数的前面0的个数,即可解答.
5.D
解:A、该式子不是一个等式,则本项不符合题意,
B、该式子中含有两个未知数,但未知数x的最高次数为2,则本项不符合题意,
C、该式子中含有两个未知数,但未知数y高次数为-1,则本项不符合题意,
D、该方程为二元一次方程,则本项符合题意,
故答案为:D.
根据二元一次方程的定义:如果一个方程含有两个未知数,并且所含未知数的项都为1次方,那么这个整式方程就叫做二元一次方程,据此逐项分析即可.
6.C
解:A x+2y 不是二元一次方程,故A项不符合题意;
B x+y-z=1含有三个未知数,不是二元一次方程,故B项不符合题意;
C 2x+y-1=0是二元一次方程,故C项符合题意;
D 不是二元一次方程,故D项不符合题意.
故答案为:C.
根据二元一次方程的定义:含有两个未知数的整式方程,即可求得.
7.D
解:① a*b=(a-b)2=(b-a)2=b*a,故①符合题意;
②(a*b)2=(a2-2ab+b2)2≠(a2-b2)2,故②不符合题意;
③a*(b-c)=(a-b+c)2,(b-c)*a=(b-c-a)2=(a-b+c)2,故③符合题意;
④a*(b+c)=(a-b-c)2=(a-b)2-2(a-b)c+c2=a2+b2+c2-2ab-2ac-2bc,
a*b+a*c=(a-b)2+(a-c)2=2a2+b2+c2-2ab-2ac,
故④不符合题意.
故答案为:D.
根据新运算计算,根据完全平方差公式计算各式,即可求得.
8.B
解:B中﹣x2和﹣y2的系数相同,故不能用平方差公式进行因式分解.
ACD中两项的符号相反,都是平方的形式,故可以用平方差公式进行因式分解.
故答案为:B.
平方差公式:
9.C
解:根据图形可得,∠A和∠B互为同旁内角.
故答案为:C.
根据同旁内角的定义判断即可,位于两条平行线的内侧,位于截线的同旁的角即为同旁内角.
10.B
A、 ,其中y≠0,不符合题意;
B、 ,其中左边隐含a≠0,符合题意;
C、 ,不符合题意.
D、根据分式基本性质知道 ,不符合题意;
故答案为:B.
根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项,且扩大(缩小)的倍数不能为0,并且分式的值不变,由此即可判定选择项.
11.B
解:(29+29+53)÷3=37,即最后三只袋中球的个数相同,
∴ 甲袋:29-2x+2x+2y=37,
丙袋:53+2y-2x-2y=37,
∴ 2y=8,2x=16,
∴ 2x+y=2x·2y=8×16=128.
故答案为:B.
先计算出最后袋中球的个数,再据此得到2y=8,2x=16,最后计算2x+y的值即可.
12.D
解:
∵ AB∥CD,
∴ ∠1=∠BCD=60°,
∴ ∠2=180°-∠BCD=120°.
故答案为:D.
根据平行线的性质可得∠1=∠BCD,根据邻补角的性质即可求得.
13.C
解:(20x3y-15x2y2+5xy)÷(-5xy)
=20x3y÷(-5xy) -15x2y2÷(-5xy) +5xy÷(-5xy)
= -4x2+3xy-1
故答案为:C.
根据多项式除单项式的法则进行运算即可.
14.C
解:由图可知:将沿射线BC平移到,对应点连线的长即为平移距离,BE满足条件
故答案为:C.
根据平移的性质即可求解.
15.B
解:A、,故选项A错误,不符合题意;
B、,故选项B正确,符合题意;
C、,故选项C错误,不符合题意;
D、,故选项D错误,不符合题意.
故答案为:B.
根据合并同类项法则,同底数幂的乘法和除法法则,幂的乘方法则,分别进行计算并判断即可.
16.B
解:A、∠1和∠2为对顶角,则本项不符合题意,
B、∠2和∠3为内错角,则本项符合题意,
C、∠1和∠3为同位角,则本项不符合题意,
D、∠2和∠4为同位角,则本项不符合题意,
故答案为:B.
根据内错角的定义:两条直线被第三条直线所截,如果两个角都在两条直线的内侧,并且在第三条直线的两侧,那么这样的一对角叫作内错角,据此逐项分析即可.
17.D
解:A、,此项错误
B、中的和指数不同,不能合并,此项错误
C、,此项错误
D、,正确
故答案为:D.
利用同底数幂相乘,底数不变,指数相加,可对A作出判断;只有同类项才能合并,可对B作出判断;利用积的乘方法则,可对C、D作出判断.
18.A
解:过点C作GF//DE于点C,如图:
∵DE//AB,
∴FG//AB//DE.
∴∠GCA=∠BAC=128°,∠CDE+∠GCD=180°,
∴∠GCD=180°-∠CDE=180°-70°=110°,
∴∠ACD=∠GCA-∠GCD=18°.
故答案为:A.
过点C作GF//DE于点C,由平行公理及推论可得FG//AB//DE.根据平行线的性质可求得∠GCA和∠GCD的度数,相减即可得到∠ACD的度数.
19.A
解:0.000326=3.26×10-4.
故答案为:A.
将大于0小于1的数表示为a×10-n,其中1≤a<10.
20.B
解:A、(a3)2=a6;
B、a6÷a3=a3;
C、a5与a3不是同类项,不能合并;
D、a2·a3=a5.
故选:B.
A、根据幂的乘方法则可得原式=a6;
B、根据同底数幂的除法法则可得原式=a3;
C、a5与a3不是同类项,不能合并;
D、根据同底数幂的乘法法则可得原式=a5.
21.D
解:∵ mn-2n+3m-9=0,
∴mn-2n+3m-6-3=0,
∴(m-2)(n+3)=3,
①m-2=1时,n+3=3,∴m=3,n=0,
∴mn=0;
②m-2=-1时,n+3=-3,∴m=1,n=-6,
∴mn=-6;
③m-2=3时,n+3=1,∴m=5,n=-2,
∴mn=-10;
④m-2=-3时,n+3=-1,∴m=-1,n=-4,
∴mn=4;
综上:mn=0或-6或-10或4,所以共有4个值.
故答案为:D
由mn-2n+ 3m-9=0可得: mn-2n+ 3m-6-3=0,即(m-2)(n+3)=3, 再分别讨论m-2=+1, ±3四种情况即可.
22.D
解:A、不是同类项,不能进行合并计算,则本项不符合题意,
B、不是同类项,不能进行合并计算,则本项不符合题意,
C、则本项不符合题意,
D、则本项符合题意,
故答案为:D.
根据合并同类项法则,幂的乘方和同底数幂的乘法计算法则计算即可求解.
23.B
解:,
②-①得,m+n=3,
故答案为:B.
利用等式性质,计算②-①即可求出答案.
24.B
解:∵,
∴,
∴,.
故答案为:B.
根据多项式乘多项式运算法则:用一个多项式的每一项乘以另一个多项式的每一项,计算后对比即可解答.
25.A
26.B
解:设正方形的边长为,
∵这两个正方形的边长之差为,
∴正方形的边长为,
∴
∵四边形、是正方形
∴
∴
∴四边形是矩形
∴
∴,
∴
即
解得:,
故答案为:B.
先设正方形的边长为,再表示正方形的边长为,根据面积关系列出关于x的方程,即可解答.
27.D
解:A、此图中的∠1与∠2不是内错角,故A不符合题意;
B、此图中的∠1与∠2不是内错角,故B不符合题意;
C、此图中的∠1与∠2不是内错角,故C不符合题意;
D、此图中的∠1与∠2是内错角,故D符合题意;
故答案为:D.
两条直线被第三条直线所截时,夹在两条直线的内部,且在截线两侧的两个角互为内错角,内错角是两条直线被第三条直线所截,可排除A、B、C,对照定义,可得答案.
28.A
解:由图(1)可得,阴影部分的面积为a2-4b2,
由图(2)可得,阴影部分的面积为(a+2b)(a-2b),
由题意可得两图中的阴影面积相同,即(a+2b)(a-2b)=a2-4b2.
故答案为:A.
根据两个阴影部分的面积即可求得平方差公式.
29.D
解:A、(a+b)2=a2+2ab+b2,故A不符合题意;
B、(a+b)2=a2+2ab+b2,故B不符合题意;
C、(a-b)2=a2-2ab+b2,故C不符合题意;
D、(a-b)2=a2-2ab+b2,故D符合题意;
故答案为:D.
利用和的完全平方公式:(a+b)2=a2+2ab+b2,可对A、B作出判断;再利用差的完全平方公式:(a-b)2=a2-2ab+b2,可对C、D作出判断.
30.B
解:∵是方程3x﹣y=5的一个解,
∴6-a=5,
解之:a=1.
故答案为:B.
将已知方程的解代入方程,可得到关于a的方程,解方程求出a的值.
31.B
解:A、该等式是整式的乘法,故选项A错误,不符合题意;
B、选项B为因式分解,该选项符合题意;
C、为分式,故选项C错误,不符合题意;
D、等号右边不是整式积的形式,故不是因式分析,故选项D错误,不符合题意.
故答案为:B.
把一个多项式分解成几个整式的积的形式即可因式分解,据此判断即可.
32.C
解:A、原式=不能运用平方差公式计算,则不符合题意,
B、原式=,不能运用平方差公式计算,则不符合题意,
C、原式=,能运用平方差公式计算,则符合题意,
D、原式=不能运用平方差公式计算,则不符合题意,
故答案为:C.
判断所给的式子能否写成两数之和乘以相同两数之差的形式即可求解.
33.D
解:平移前后图形的形状和大小不变,故ABC不符合题意,D项符合题意.
故答案为:D.
根据图形的平移的前后变化即可求得.
34.C
解:要消去x,可以将①×5-②×2可得19y=12,故A项不符合题意,C项符合题意;
要消去y,可以将①×2+②×3可得19x=39,故B,D项不符合题意.
故答案为:C.
根据二元一次方程组的加减消元法,即可求得.
35.B
解:如图,
直尺的两边互相平行,
,
,
故答案为:.
根据平行线的性质、邻补角的定义、及直角三角形的性质即可解答.
36.C
37.A
解:A、(3x+5y)(5y﹣3x) ,能用平方差公式计算,故A符合题意;
B、(m﹣n)(n﹣m) =-(m-n)2,不能用平方差公式,故B不符合题意;
C、(p+q)(﹣p﹣q) =-(p+q)2,不能用平方差公式,故C不符合题意;
D、 (2a+3b)(3a﹣2b),不能用平方差公式,故D不符合题意;
故答案为:A.
利用平方差公式(a+b)(a-b)=a2-b2,是两数的和乘以这两个数的差等于这两个数的平方差,可对A作出判断;将B、C进行转化,它们能用完全平方公式,可对B、C作出判断;而D选项中相同字母的数字不符合平方差公式,据此可得答案.
38.A
解:如图,
∵
∴
∵
∴
∵
∴
故答案为:A.
根据平行线的性质得到:进而得到最后根据平角的定义和角的运算得到进而即可求解.
39.B
解:
故答案为:B.
根据同底数幂乘法法则:同底数幂相乘,底数不变,指数相加,即可解答.
40.B
解:
①×2得
6x+10y=12③,
由②-③得
5y=4,
解之:,
把代入①得
解之:
∴方程组的解为
∵ 方程组的解也是方程3x+ky=10的解,
∴
解之:k=10.
故答案为:B.
利用加减消元法求出方程组的解,再将方程组的解代入方程3x+ky=10,可得到关于k的方程,解方程求出k的值.
41.D
解: 4x2+3mx+9 =(2x±3)2= 4x2±2·2x·3+9
故3m=±2·2·3=±12,
故m=±4
故答案为:D.
(a+b)2=a2+2ab+b2,(a+b)2=a2+2ab+b2.题干中m的正负未知,两种情况都要考虑.
42.A
解: (x+a)(2x2+bx3) =-2x3+(2a+b)x2+(3-ab)x-3a,
∵ 化简(x+a)(2x2+bx3)的结果不含x的二次项,
∴2a+b=0,
解之:b=-2a,
∴ 36a﹣18b﹣1=36a-36a-1=-1.
故答案为:A.
利用多项式乘以多项式的法则,将代数式先去括号,再合并同类项,根据化简(x+a)(2x2+bx3)的结果不含x的二次项,可得到b=-2a,将其代入代数式进行计算,可求出结果.
43.D
解:A、经过直线外一点,有且只有一条直线与已知直线平行,则本项不符合题意,
B、在同一平面内,垂直于同一条直线的两条直线互相平行,则本项不符合题意,
C、两条直线被第三条直线所截,截得的同位角不一定相等,则本项符合题意,
D、在同一个平面内,不相交的两条直线是平行线,则本项不符合题意,
故答案为:C.
根据平行线的性质逐项分析即可求解.
44.D
解:A、B、C中的与不是同位角,D中的与是同位角;
故答案为:D.
根据同位角的定义解答.
45.B
解:设人数为x人,物价为y钱,
∴,
故答案为:B.
设人数为x人,物价为y钱,根据"每人出8钱,会多出3钱",据此得到方程根据"每人出7钱,又差4钱",据此得到方程:联立两个方程即可得到方程组.
46.A
解:设“●、▲、■”的重量分别为x,y,z,根据题意得
解之:
∴x+y=2z+3z=5z.
故答案为:A.
设“●、▲、■”的重量分别为x,y,z,根据前两个图形可得到关于x,y,z的方程,解方程可表示出x,y,再求出x+y的值即可.
47.D
解:原式=
=
∵,
∴原式值为
故答案为:D.
利用完全平方公式和平方差公式计算得到原式为进而把 代入计算即可求解.
48.D
∵∠1=∠2,∠5=∠1(对顶角相等),∴∠2=∠5,∴a∥b(同位角相等,得两直线平行);∴∠3=∠6=55°(两直线平行,内错角相等),故∠4=180°-55°=125°(邻补角互补).
故选D.
解答此题的关键是注意平行线的性质和判定定理的综合运用。
49.C
解:A.只含一个未知数,是一元一次方程,不是二元一次方程,故不符合题意;
B.的分母含未知数,是分式方程,不是二元一次方程,故不符合题意;
C.是二元一次方程,符合题意;
D.整理得,最高次项的次数是2,是二元二次方程,不是二元一次方程,故不符合题意.
故答案为:C.
方程的两边都是整式,含有两个未知数,并且含未知数的项的次数都是1次的方程叫做二元一次方程.根据二元一次方程的定义一 一判断即可.
50.B
解:由图可知:
∴
∵
∴
∴阴影部分面积是:
故答案为:B.
用含a和b的式子表示长方形的长和宽,进而求出a和b的值;最后用大长方形的面积减去4个小长方形的面积,进而即可求解.
1.(2024七下·杭州期中)如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
2.(2024七下·浦江期中)若分式的值为零, 则x 的值为( )
A.x = 2 B.x = -2
C.x = 2或x= -2 D.x = 3
3.(2024七下·浦江期中)某种生物细胞的直径是0.000000012cm,用科学记数法表示,正确的是 ( )
A.12 ×10-7 cm B.1.2 ×10-7 cm
C.12 ×10-8 cm D.1.2 ×10-8 cm
4.(2024七下·温州期中) 石墨烯理论厚度是,数据用科学记数法表示为( )
A. B. C. D.
5.(2024七下·开化期中)下列是二元一次方程的是( )
A. B. C. D.
6.(2024·七下婺城期中)下列方程是二元一次方程的是( )
A. B. C. D.
7.(2024·七下婺城期中) 设a,b是实数,定义一种新运算:.下面有四个推断:
①,②,③,④.
其中推断正确的是( )
A.①②③④ B.①③④ C.①② D.①③
8.(2024七下·浦江期中)下列多项式不能用平方差公式因式分解的是( )
A.-m2+4 B.-x2-y2
C.x2y2-1 D.(m-a)2-(m+a)2
9.(2024七下·浦江期中)如图所示,∠A,∠B之间的位置关系是( )
A.互为同位角 B.互为内错角
C.互为同旁内角 D.互为对顶角
10.(2024·七下婺城期中)下列等式从左到右的变形正确的是( )
A. B. C. D.
11.(2024·七下婺城期中) 如图,在甲、乙、丙三只袋中分别装有球29个、29个、53个,先从甲袋中取出个球放入乙袋,再从乙袋中取出个球放入丙袋,最后从丙袋中取出球放入甲袋,此时三只袋中球的个数相同,则的值等于( )
A.512 B.128 C.64 D.32
12.(2024·七下婺城期中)一杆古秤在称物时的状态如图所示,已知,则的度数为( )
A.20° B.70° C.110° D.120°
13.(2024七下·浦江期中)化简(20x3y-15x2y2+5xy)÷(-5xy) 的结果( )
A.4x2-3xy+1 B.4x2-3xy C.-4x2+3xy-1 D.-4x2+3xy
14.(2024七下·开化期中)如图,将沿射线BC平移到,则下列线段的长度表示平移距离的是( )
A.BC B.BF C.BE D.CE
15.(2024七下·浦江期中)下列计算正确的是 ( )
A. B. C. D.
16.(2024七下·开化期中)如图,在所标识的角中,内错角是( )
A.和 B.和 C.和 D.和
17.(2024七下·杭州期中)下列运算正确的是( )
A. B. C. D.
18.(2024七下·浦江期中)数学兴趣小组同学利用几何图形画出螳螂的简笔画如图所示,已知∠BAC=128°,且∠CDE=70°,则∠ACD=( )
A.18° B.58° C.48° D.38 °
19.(2024·七下婺城期中)小时候我们用肥皂水吹泡泡,泡沫的厚度约为0.000326毫米,将数据0.000326用科学记数法表示为( )
A. B.
C. D.
20.(2024·七下婺城期中)下列计算正确的是( )
A. B. C. D.
21.(2024七下·邵阳期末)已知m,n是整数,且mn-2n+3m-9=0,则mn的值有( )个
A.1个 B.2个 C.3个 D.4个
22.(2024七下·开化期中)可以表示为( )
A. B. C. D.
23.(2024七下·温州期中) 已知二元一次方程组,则的值是( )
A.9 B.3 C. D.
24.(2024七下·西湖期中) 如果,那么的值分别是( )
A. B.
C. D.
25.(2024七下·杭州期中) 我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B.
C. D.
26.(2024七下·温州期中) 如图,将正方形与正方形叠在一起,且这两个正方形的边长之差为,两个正方形相交于点M、N,连结,,若阴影部分的面积是9,,,则正方形的边长为( )
A. B.4 C.4.2 D.4.5
27.(2024七下·杭州期中)下列图形中,∠1与∠2是内错角的是( )
A. B.
C. D.
28.(2024·七下婺城期中)如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( )
A.(a﹣2b)(a+2b)=a2﹣4b2 B.(a+2b)2=a2+4ab+b2
C.(a﹣2b)2=a2﹣4ab+b2 D.(a+b)2=a2+2ab+b2
29.(2024七下·杭州期中)下列计算正确的是( )
A.(a+b)2=a2+b2 B.(a+b)2=a2+ab+b2
C.(a-b)2=a2+2ab-b2 D.(a-b)2=a2-2ab+b2
30.(2024七下·杭州期中)已知是方程3x﹣y=5的一个解,则a的值为( )
A.a=﹣1 B.a=1 C. D.
31.(2024七下·浦江期中)下列从左到右的变形是因式分解的是 ( )
A.2m(m-n)=2m2-2mn B.5x2y-10xy2=5xy(x-2y)
C.x2+1=x(x+) D.x2-3x+1=x(x-3)+1
32.(2024七下·开化期中)下列能用平方差公式直接计算的是( )
A. B.
C. D.
33.(2024·七下婺城期中)下图是2024年将在法国巴黎举行的夏季奥运会图标,平移该图标可以得到的图形是( )
A. B. C. D.
34.(2024·七下婺城期中)利用加减消元法解方程组,下列做法正确的是( )
A.要消去x,可以将①×5+②×2 B.要消去y,可以将①×5-②×3
C.要消去x,可以将①×5-②×2 D.要消去y,可以将①×2-②×3
35.(2024七下·温州期中) 如图,一块直尺与一个直角三角形如图放置,若,则的度数为( )
A. B. C. D.
36.(2024七下·温州期中) 一个正方形的边长增加,面积相应增加,则这个正方形的边长为( )
A.8 B.5 C.6 D.7
37.(2024七下·杭州期中)下列各式中,能用平方差公式计算的是( )
A.(3x+5y)(5y﹣3x) B.(m﹣n)(n﹣m)
C.(p+q)(﹣p﹣q) D.(2a+3b)(3a﹣2b)
38.(2024七下·开化期中)如图,将一块三角板中含有60°角的顶点放在直尺的一边上,若,那么的度数为( )
A.80° B.70° C.40° D.30°
39.(2024七下·永寿期中)的运算结果为( )
A. B. C. D.
40.(2024七下·杭州期中)若方程组的解也是方程3x+ky=10的解,则k的值是( )
A. B. C. D.
41.(2024七下·浦江期中)代数式4x2+3mx+9能写成一个整式的完全平方的形式,则 m= ( )
A.12 B.±12 C.4 D.±4
42.(2024七下·杭州期中)已知a,b是常数,若化简(x+a)(2x2+bx3)的结果不含x的二次项,则36a﹣18b﹣1的值为( )
A.﹣1 B.0 C.17 D.35
43.(2024七下·开化期中)下列说法错误的是( )
A.经过直线外一点,有且只有一条直线与已知直线平行.
B.在同一平面内,垂直于同一条直线的两条直线互相平行.
C.两条直线被第三条直线所截,截得的同位角相等.
D.在同一个平面内,不相交的两条直线是平行线.
44.(2024七下·温州期中) 下列图形中,与是同位角的是( )
A. B.
C. D.
45.(2024七下·开化期中)《九章算术》中记载了一道有趣的数学问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱,问人数、物价各多少?”设人数为x人,物价为y钱,根据题意,可列方程组( )
A. B.
C. D.
46.(2024七下·杭州期中)设“●、▲、■”分别表示三种不同的物体.如图所示,前两架天平保持平衡,如果要使第三架天平也保持平衡,那么“?”处应放“■”的个数为( )
A.5 B.4 C.3 D.2
47.(2024七下·开化期中)若代数式,则的值是( )
A. B.0 C.1 D.2
48.(2024七下·杭州期中)如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
49.(2024七下·温州期中) 下列各式是二元一次方程的是( )
A. B.
C. D.
50.(2024七下·开化期中)图1是一种长为a宽为b的长方形,将这样四个形状和大小完全相同的长方形摆放在一个长为5宽为4的大长方形中,如图2所示,则图2中阴影部分面积是( )
A.8 B.12 C.15 D.16
答案解析部分
1.C
解:由平移的性质可知:AD=BE=CF=1,
∵EC=2,
∴BF=BE+CE+CF=1+2+1=4,
故答案为:C.
根据平移的性质可知:AD=BE=CF=1,将代入求解即可。
2.B
解:∵ 分式的值为零,
∴x-2≠0,且x2-4=0,
解得:x=﹣2.
故答案为:B.
当分式满足,A=0且B≠0.
3.D
解:0.000000012=1.2×10-8.
故答案为:D.
大于0小于1的数用科学记数法表示为a×10-n,其中1≤a<10,n为原数字从左往右数第一个不为0的数字前面的0的个数.
4.A
解:,
故答案为:A.
用科学记数法表示绝对值小于1的数,用科学记数法表示为,其中,的值为第一个不为0的数的前面0的个数,即可解答.
5.D
解:A、该式子不是一个等式,则本项不符合题意,
B、该式子中含有两个未知数,但未知数x的最高次数为2,则本项不符合题意,
C、该式子中含有两个未知数,但未知数y高次数为-1,则本项不符合题意,
D、该方程为二元一次方程,则本项符合题意,
故答案为:D.
根据二元一次方程的定义:如果一个方程含有两个未知数,并且所含未知数的项都为1次方,那么这个整式方程就叫做二元一次方程,据此逐项分析即可.
6.C
解:A x+2y 不是二元一次方程,故A项不符合题意;
B x+y-z=1含有三个未知数,不是二元一次方程,故B项不符合题意;
C 2x+y-1=0是二元一次方程,故C项符合题意;
D 不是二元一次方程,故D项不符合题意.
故答案为:C.
根据二元一次方程的定义:含有两个未知数的整式方程,即可求得.
7.D
解:① a*b=(a-b)2=(b-a)2=b*a,故①符合题意;
②(a*b)2=(a2-2ab+b2)2≠(a2-b2)2,故②不符合题意;
③a*(b-c)=(a-b+c)2,(b-c)*a=(b-c-a)2=(a-b+c)2,故③符合题意;
④a*(b+c)=(a-b-c)2=(a-b)2-2(a-b)c+c2=a2+b2+c2-2ab-2ac-2bc,
a*b+a*c=(a-b)2+(a-c)2=2a2+b2+c2-2ab-2ac,
故④不符合题意.
故答案为:D.
根据新运算计算,根据完全平方差公式计算各式,即可求得.
8.B
解:B中﹣x2和﹣y2的系数相同,故不能用平方差公式进行因式分解.
ACD中两项的符号相反,都是平方的形式,故可以用平方差公式进行因式分解.
故答案为:B.
平方差公式:
9.C
解:根据图形可得,∠A和∠B互为同旁内角.
故答案为:C.
根据同旁内角的定义判断即可,位于两条平行线的内侧,位于截线的同旁的角即为同旁内角.
10.B
A、 ,其中y≠0,不符合题意;
B、 ,其中左边隐含a≠0,符合题意;
C、 ,不符合题意.
D、根据分式基本性质知道 ,不符合题意;
故答案为:B.
根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项,且扩大(缩小)的倍数不能为0,并且分式的值不变,由此即可判定选择项.
11.B
解:(29+29+53)÷3=37,即最后三只袋中球的个数相同,
∴ 甲袋:29-2x+2x+2y=37,
丙袋:53+2y-2x-2y=37,
∴ 2y=8,2x=16,
∴ 2x+y=2x·2y=8×16=128.
故答案为:B.
先计算出最后袋中球的个数,再据此得到2y=8,2x=16,最后计算2x+y的值即可.
12.D
解:
∵ AB∥CD,
∴ ∠1=∠BCD=60°,
∴ ∠2=180°-∠BCD=120°.
故答案为:D.
根据平行线的性质可得∠1=∠BCD,根据邻补角的性质即可求得.
13.C
解:(20x3y-15x2y2+5xy)÷(-5xy)
=20x3y÷(-5xy) -15x2y2÷(-5xy) +5xy÷(-5xy)
= -4x2+3xy-1
故答案为:C.
根据多项式除单项式的法则进行运算即可.
14.C
解:由图可知:将沿射线BC平移到,对应点连线的长即为平移距离,BE满足条件
故答案为:C.
根据平移的性质即可求解.
15.B
解:A、,故选项A错误,不符合题意;
B、,故选项B正确,符合题意;
C、,故选项C错误,不符合题意;
D、,故选项D错误,不符合题意.
故答案为:B.
根据合并同类项法则,同底数幂的乘法和除法法则,幂的乘方法则,分别进行计算并判断即可.
16.B
解:A、∠1和∠2为对顶角,则本项不符合题意,
B、∠2和∠3为内错角,则本项符合题意,
C、∠1和∠3为同位角,则本项不符合题意,
D、∠2和∠4为同位角,则本项不符合题意,
故答案为:B.
根据内错角的定义:两条直线被第三条直线所截,如果两个角都在两条直线的内侧,并且在第三条直线的两侧,那么这样的一对角叫作内错角,据此逐项分析即可.
17.D
解:A、,此项错误
B、中的和指数不同,不能合并,此项错误
C、,此项错误
D、,正确
故答案为:D.
利用同底数幂相乘,底数不变,指数相加,可对A作出判断;只有同类项才能合并,可对B作出判断;利用积的乘方法则,可对C、D作出判断.
18.A
解:过点C作GF//DE于点C,如图:
∵DE//AB,
∴FG//AB//DE.
∴∠GCA=∠BAC=128°,∠CDE+∠GCD=180°,
∴∠GCD=180°-∠CDE=180°-70°=110°,
∴∠ACD=∠GCA-∠GCD=18°.
故答案为:A.
过点C作GF//DE于点C,由平行公理及推论可得FG//AB//DE.根据平行线的性质可求得∠GCA和∠GCD的度数,相减即可得到∠ACD的度数.
19.A
解:0.000326=3.26×10-4.
故答案为:A.
将大于0小于1的数表示为a×10-n,其中1≤a<10.
20.B
解:A、(a3)2=a6;
B、a6÷a3=a3;
C、a5与a3不是同类项,不能合并;
D、a2·a3=a5.
故选:B.
A、根据幂的乘方法则可得原式=a6;
B、根据同底数幂的除法法则可得原式=a3;
C、a5与a3不是同类项,不能合并;
D、根据同底数幂的乘法法则可得原式=a5.
21.D
解:∵ mn-2n+3m-9=0,
∴mn-2n+3m-6-3=0,
∴(m-2)(n+3)=3,
①m-2=1时,n+3=3,∴m=3,n=0,
∴mn=0;
②m-2=-1时,n+3=-3,∴m=1,n=-6,
∴mn=-6;
③m-2=3时,n+3=1,∴m=5,n=-2,
∴mn=-10;
④m-2=-3时,n+3=-1,∴m=-1,n=-4,
∴mn=4;
综上:mn=0或-6或-10或4,所以共有4个值.
故答案为:D
由mn-2n+ 3m-9=0可得: mn-2n+ 3m-6-3=0,即(m-2)(n+3)=3, 再分别讨论m-2=+1, ±3四种情况即可.
22.D
解:A、不是同类项,不能进行合并计算,则本项不符合题意,
B、不是同类项,不能进行合并计算,则本项不符合题意,
C、则本项不符合题意,
D、则本项符合题意,
故答案为:D.
根据合并同类项法则,幂的乘方和同底数幂的乘法计算法则计算即可求解.
23.B
解:,
②-①得,m+n=3,
故答案为:B.
利用等式性质,计算②-①即可求出答案.
24.B
解:∵,
∴,
∴,.
故答案为:B.
根据多项式乘多项式运算法则:用一个多项式的每一项乘以另一个多项式的每一项,计算后对比即可解答.
25.A
26.B
解:设正方形的边长为,
∵这两个正方形的边长之差为,
∴正方形的边长为,
∴
∵四边形、是正方形
∴
∴
∴四边形是矩形
∴
∴,
∴
即
解得:,
故答案为:B.
先设正方形的边长为,再表示正方形的边长为,根据面积关系列出关于x的方程,即可解答.
27.D
解:A、此图中的∠1与∠2不是内错角,故A不符合题意;
B、此图中的∠1与∠2不是内错角,故B不符合题意;
C、此图中的∠1与∠2不是内错角,故C不符合题意;
D、此图中的∠1与∠2是内错角,故D符合题意;
故答案为:D.
两条直线被第三条直线所截时,夹在两条直线的内部,且在截线两侧的两个角互为内错角,内错角是两条直线被第三条直线所截,可排除A、B、C,对照定义,可得答案.
28.A
解:由图(1)可得,阴影部分的面积为a2-4b2,
由图(2)可得,阴影部分的面积为(a+2b)(a-2b),
由题意可得两图中的阴影面积相同,即(a+2b)(a-2b)=a2-4b2.
故答案为:A.
根据两个阴影部分的面积即可求得平方差公式.
29.D
解:A、(a+b)2=a2+2ab+b2,故A不符合题意;
B、(a+b)2=a2+2ab+b2,故B不符合题意;
C、(a-b)2=a2-2ab+b2,故C不符合题意;
D、(a-b)2=a2-2ab+b2,故D符合题意;
故答案为:D.
利用和的完全平方公式:(a+b)2=a2+2ab+b2,可对A、B作出判断;再利用差的完全平方公式:(a-b)2=a2-2ab+b2,可对C、D作出判断.
30.B
解:∵是方程3x﹣y=5的一个解,
∴6-a=5,
解之:a=1.
故答案为:B.
将已知方程的解代入方程,可得到关于a的方程,解方程求出a的值.
31.B
解:A、该等式是整式的乘法,故选项A错误,不符合题意;
B、选项B为因式分解,该选项符合题意;
C、为分式,故选项C错误,不符合题意;
D、等号右边不是整式积的形式,故不是因式分析,故选项D错误,不符合题意.
故答案为:B.
把一个多项式分解成几个整式的积的形式即可因式分解,据此判断即可.
32.C
解:A、原式=不能运用平方差公式计算,则不符合题意,
B、原式=,不能运用平方差公式计算,则不符合题意,
C、原式=,能运用平方差公式计算,则符合题意,
D、原式=不能运用平方差公式计算,则不符合题意,
故答案为:C.
判断所给的式子能否写成两数之和乘以相同两数之差的形式即可求解.
33.D
解:平移前后图形的形状和大小不变,故ABC不符合题意,D项符合题意.
故答案为:D.
根据图形的平移的前后变化即可求得.
34.C
解:要消去x,可以将①×5-②×2可得19y=12,故A项不符合题意,C项符合题意;
要消去y,可以将①×2+②×3可得19x=39,故B,D项不符合题意.
故答案为:C.
根据二元一次方程组的加减消元法,即可求得.
35.B
解:如图,
直尺的两边互相平行,
,
,
故答案为:.
根据平行线的性质、邻补角的定义、及直角三角形的性质即可解答.
36.C
37.A
解:A、(3x+5y)(5y﹣3x) ,能用平方差公式计算,故A符合题意;
B、(m﹣n)(n﹣m) =-(m-n)2,不能用平方差公式,故B不符合题意;
C、(p+q)(﹣p﹣q) =-(p+q)2,不能用平方差公式,故C不符合题意;
D、 (2a+3b)(3a﹣2b),不能用平方差公式,故D不符合题意;
故答案为:A.
利用平方差公式(a+b)(a-b)=a2-b2,是两数的和乘以这两个数的差等于这两个数的平方差,可对A作出判断;将B、C进行转化,它们能用完全平方公式,可对B、C作出判断;而D选项中相同字母的数字不符合平方差公式,据此可得答案.
38.A
解:如图,
∵
∴
∵
∴
∵
∴
故答案为:A.
根据平行线的性质得到:进而得到最后根据平角的定义和角的运算得到进而即可求解.
39.B
解:
故答案为:B.
根据同底数幂乘法法则:同底数幂相乘,底数不变,指数相加,即可解答.
40.B
解:
①×2得
6x+10y=12③,
由②-③得
5y=4,
解之:,
把代入①得
解之:
∴方程组的解为
∵ 方程组的解也是方程3x+ky=10的解,
∴
解之:k=10.
故答案为:B.
利用加减消元法求出方程组的解,再将方程组的解代入方程3x+ky=10,可得到关于k的方程,解方程求出k的值.
41.D
解: 4x2+3mx+9 =(2x±3)2= 4x2±2·2x·3+9
故3m=±2·2·3=±12,
故m=±4
故答案为:D.
(a+b)2=a2+2ab+b2,(a+b)2=a2+2ab+b2.题干中m的正负未知,两种情况都要考虑.
42.A
解: (x+a)(2x2+bx3) =-2x3+(2a+b)x2+(3-ab)x-3a,
∵ 化简(x+a)(2x2+bx3)的结果不含x的二次项,
∴2a+b=0,
解之:b=-2a,
∴ 36a﹣18b﹣1=36a-36a-1=-1.
故答案为:A.
利用多项式乘以多项式的法则,将代数式先去括号,再合并同类项,根据化简(x+a)(2x2+bx3)的结果不含x的二次项,可得到b=-2a,将其代入代数式进行计算,可求出结果.
43.D
解:A、经过直线外一点,有且只有一条直线与已知直线平行,则本项不符合题意,
B、在同一平面内,垂直于同一条直线的两条直线互相平行,则本项不符合题意,
C、两条直线被第三条直线所截,截得的同位角不一定相等,则本项符合题意,
D、在同一个平面内,不相交的两条直线是平行线,则本项不符合题意,
故答案为:C.
根据平行线的性质逐项分析即可求解.
44.D
解:A、B、C中的与不是同位角,D中的与是同位角;
故答案为:D.
根据同位角的定义解答.
45.B
解:设人数为x人,物价为y钱,
∴,
故答案为:B.
设人数为x人,物价为y钱,根据"每人出8钱,会多出3钱",据此得到方程根据"每人出7钱,又差4钱",据此得到方程:联立两个方程即可得到方程组.
46.A
解:设“●、▲、■”的重量分别为x,y,z,根据题意得
解之:
∴x+y=2z+3z=5z.
故答案为:A.
设“●、▲、■”的重量分别为x,y,z,根据前两个图形可得到关于x,y,z的方程,解方程可表示出x,y,再求出x+y的值即可.
47.D
解:原式=
=
∵,
∴原式值为
故答案为:D.
利用完全平方公式和平方差公式计算得到原式为进而把 代入计算即可求解.
48.D
∵∠1=∠2,∠5=∠1(对顶角相等),∴∠2=∠5,∴a∥b(同位角相等,得两直线平行);∴∠3=∠6=55°(两直线平行,内错角相等),故∠4=180°-55°=125°(邻补角互补).
故选D.
解答此题的关键是注意平行线的性质和判定定理的综合运用。
49.C
解:A.只含一个未知数,是一元一次方程,不是二元一次方程,故不符合题意;
B.的分母含未知数,是分式方程,不是二元一次方程,故不符合题意;
C.是二元一次方程,符合题意;
D.整理得,最高次项的次数是2,是二元二次方程,不是二元一次方程,故不符合题意.
故答案为:C.
方程的两边都是整式,含有两个未知数,并且含未知数的项的次数都是1次的方程叫做二元一次方程.根据二元一次方程的定义一 一判断即可.
50.B
解:由图可知:
∴
∵
∴
∴阴影部分面积是:
故答案为:B.
用含a和b的式子表示长方形的长和宽,进而求出a和b的值;最后用大长方形的面积减去4个小长方形的面积,进而即可求解.
同课章节目录
