2024-2025学年浙教版七年级数学下册期中真题专项复习06填空题(含答案)(浙江专用)
文档属性
| 名称 | 2024-2025学年浙教版七年级数学下册期中真题专项复习06填空题(含答案)(浙江专用) |

|
|
| 格式 | docx | ||
| 文件大小 | 304.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览




文档简介
2024-2025学年七年级数学下册期中真题专项复习01填空题
1.(2024七下·杭州期中)计算:
2.(2024七下·临平期中)已知,用含的代数式表示,则 .
3.(2024七下·城厢期中)如图,将向右平移5个单位长度得到,且点B,E,C,F在同一条直线上,若,则的长度是 .
4.(2024七下·瑞安期中)端午节快到了,商店准备推出粽子礼盒,若3个粽子装一盒则装完还多2个礼盒,若2个粽子装一盒还多6个粽子.设有个礼盒,个粽子,所满足的关系式为( )
A. B.
C. D.
5.(2024七下·瑞安期中) 如图,与为同旁内角的是( )
A. B. C. D.
6.(2024·宿迁模拟)下列计算正确的是( )
A. B. C. D.
7.(2024七下·瑞安期中)碳纳米管,又名巴基管,是一种具有特殊结构的一维量子材料,其直径一般为厘米,其中用科学记数法表示为( )
A. B. C. D.
8.(2024七下·瑞安期中)下列计算正确的是( )
A. B.
C. D.
9.(2024七下·临平期中)若 ,则 .
10.(2024七下·临平期中)已知是二元一次方程的一组解,则 .
11.(2024七下·瑞安期中)已知,,则的值为( )
A.8 B.20 C.4 D.16
12.(2024七下·杭州期中)已知关于,的二元一次方程组的解为,则关于,的二元一次方程组的解为 .
13.(2024七下·瑞安期中)下列不属于平移现象的是( )
A.升降电梯上下移动 B.传送带上物品传输
C.拉抽屉 D.电风扇扇叶转动
14.(2024七下·杭州期中)已知方程,用含的代数式表示,则
15.(2024七下·成都期中)已知:m+2n﹣2=0,则3m 9n的值为 .
16.(2024七下·瑞安期中) 已知 是方程的一个解,则m的值为( )
A. B. C. D.
17.(2024七下·瑞安期中) 下列多项式相乘,可以用平方差公式计算的是( )
A. B.
C. D.
18.(2024七下·杭州期中)如图,两条平行直线,被直线所截,点位于两平行线之间,且在直线右侧,点是上一点,位于点右侧.小明进行了如下操作:连结,,在平分线上取一点,过点作,交直线于点.记,,,则 (用含,的代数式表示).
19.(2024七下·余杭期中)如图1,将一条两边互相平行的长方形纸带沿折叠,设度.
图1 图2
(1)若,则 度.
(2)将图1纸带继续沿折叠成图2,则 度.(用含的代数式表示)
20.(2024七下·瑞安期中) 将一副三角板按如图的方式摆放,已知,则的度数为( )
A. B. C. D.
21.(2024七下·瑞安期中) 已知方程组,则= .
22.(2024七下·新昌期中)芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000209kg,将0.00000209用科学记数法表示为( )
A. B.
C. D.
23.(2024七下·瑞安期中)如图,在长方形ABCD中,有正方形FGBE,正方形DMNH和正方形HKEC.S1,S2分别表示正方形FGBE,正方形DMNH的面积,若AB-BC=1,S1+S2=8,则阴影部分的面积是 .
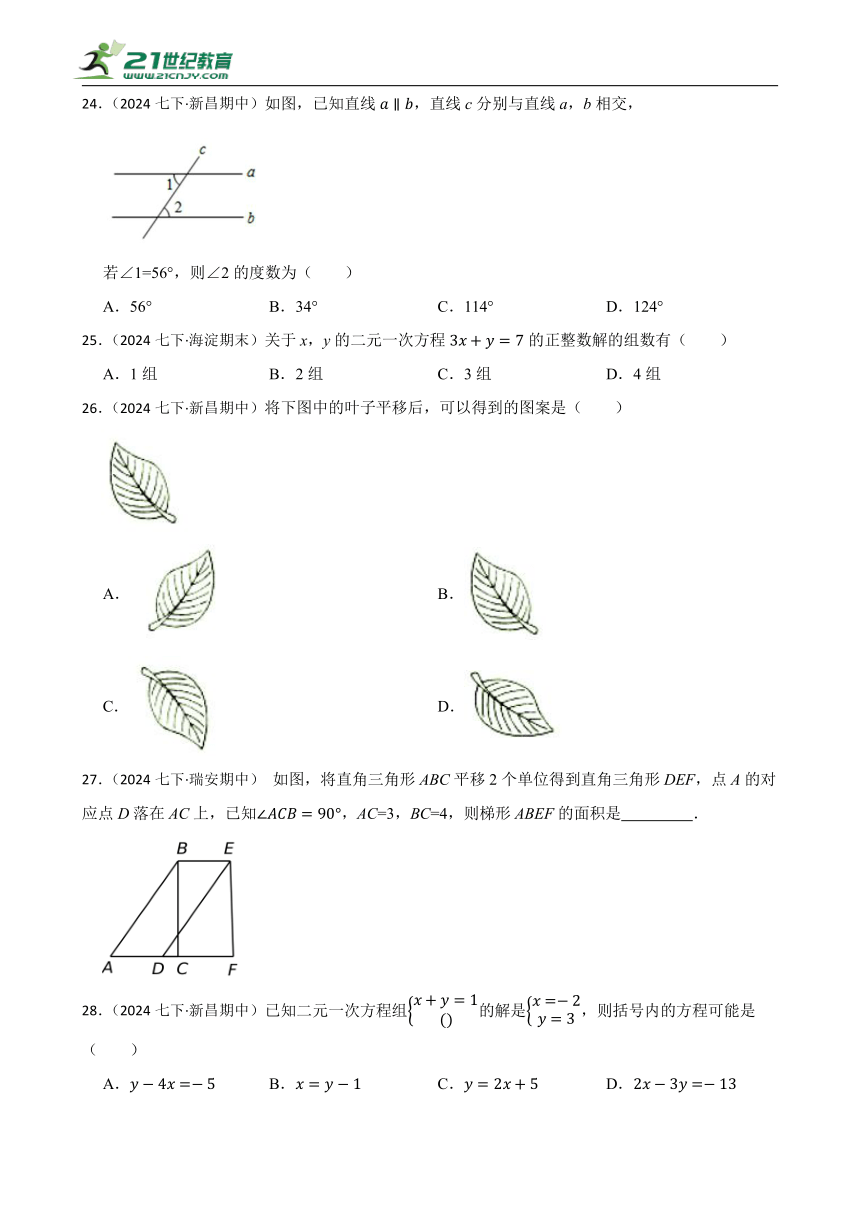
24.(2024七下·新昌期中)如图,已知直线,直线c分别与直线a,b相交,
若∠1=56°,则∠2的度数为( )
A.56° B.34° C.114° D.124°
25.(2024七下·海淀期末)关于x,y的二元一次方程的正整数解的组数有( )
A.1组 B.2组 C.3组 D.4组
26.(2024七下·新昌期中)将下图中的叶子平移后,可以得到的图案是( )
A. B.
C. D.
27.(2024七下·瑞安期中) 如图,将直角三角形ABC平移2个单位得到直角三角形DEF,点A的对应点D落在AC上,已知,AC=3,BC=4,则梯形ABEF的面积是 .
28.(2024七下·新昌期中)已知二元一次方程组的解是,则括号内的方程可能是( )
A. B. C. D.
29.(2024七下·新昌期中)如图,下面四个条件中不能得到AB∥CD的是( )
A.∠B=∠1 B.∠A=∠2
C.∠B=∠BCD D.∠B+∠BCD=180°
30.(2024七下·新昌期中)已知 , ,则 的值为( )
A.1 B.2 C.4 D.
31.(2024七下·瑞安期中)如图,AB∥CD,∠1=50°,则∠2= °.
32.(2024七下·新昌期中)有两个正方形 ,将 并列放置后构造新的图形,分别得到长方形图甲与正方形图乙. 若图甲、图乙中阴影的面积分别为 14 与 36 ,则正方形 的面积为( )
A.3 B.4 C.5 D.6
33.(2024七下·开化期中)如图,在所标识的角中,内错角是( )
A.和 B.和 C.和 D.和
34.(2024七下·蒸湘期末)我国古代数学著作九章算术记载了一道“牛马问题”:“今有二马、一牛价过一万,如半马之价.一马、二牛价不满一万,如半牛之价.问牛、马价各几何.”其大意为:现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱,求一匹马、一头牛各多少钱?设一匹马价钱为元,一头牛价钱为元,则符合题意的方程组是( )
A.
B.
C.
D.
35.(2024七下·杭州期中)如图,将一条长方形纸片沿AB折叠,已知∠DAB=70°,则∠CBF= .
36.(2024七下·杭州期中)如图,将三角形平移得到三角形,若图中阴影部分面积与所有空白部分面积之比为,则阴影部分面积与三角形面积的比值为 .
37.(2024七下·瑞安期中) 计算:= .
38.(2024七下·瑞安期中)如图,把长方形纸条沿EF,GH折叠(点E,H在AD 边上,点F,G在BC边上),A点的对称点为点,D点的对称点为点,若线段落在边E上,∠EH=32°,则∠BFE等于( )
A.58° B.61° C.62° D.64°
39.(2024七下·瑞安期中) 已知方程,用关于的代数式表示,则= .
答案解析部分
1.6a3b
解:2a2b 3a=6a3b.
故答案为:6a3b.
根据单项式与单项式相乘,把他们的系数,相同字母的幂分别相乘,对于只在某一个单项式含有的字母则连同指数作为积的一个因式,计算即可.
2.5b+2
解:由等式的性质得a=2+5b
故答案为:5b+2.
直接由等式的性质进行移项便可得结果.
3.8
4.A
解:根据条件“ 若3个粽子装一盒则装完还多2个礼盒 ”,即用(x-2)个礼盒,每个礼盒装3个粽子刚好装完y个粽子,于是有3(x-2)=y;根据条件“ 若2个粽子装一盒还多6个粽子 ”,即用x个礼盒,每个礼盒装2个粽子下,还剩6个粽子,于是有2x+6=y.
因此,得到二元一次方程组.
故答案为:A.
要抓住等量关系的重点,即不论哪种包装方式,粽子的数量保持不变.
5.D
解:根据图片,∠5的同旁内角为∠4.
故答案为:D.
同旁内角的定义: 两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角.
6.D
解:对A,正确结果应为m5; 对于B,正确结果应为9m2; 对于C,正确结果应为m4;D正确;
故答案为:D.
根据同底数幂的乘法、除法、乘方的规则进行一 一判断即可.
7.B
解:当小数点向右移动到4后时,共移动7位,故为4.0x10-7.
故答案为:B.
科学记数法表示大于0小于1的数:ax10n,其中1≤a<10,且n为负整数,为小数点向右移动到第1个非零数后面时,小数点移动的位数.
8.C
解:A、,A错误;
B、a3+a4无法合并同类项,B错误;
C、计算无误,C正确;
D、,D错误.
故答案为:C.
根据同底数幂的乘除法、合并同类项法则、积的乘方法则等逐一检验各选项即可.
9.-2
解:∵(x+3)(x 5)= x2 5x+3x 15=x2 2x 15,
∴m= 2.
故答案为: 2.
根据多项式与多项式的乘法法则将左式展开并合并同类项,然后根据多项式的性质可得m的值.
10.2023
解:将x=1,y=-1代入方程可得2a-b=-1,于是2a-b+2024=-1+2024=2023
故答案为:2023.
将解代入方程再进行整体代换可得结果.
11.C
解:∵,,
∴
∴.
故答案为:C.
解题关键是结合完全平方公式先计算出的值.
12.
解:由,得:
,
设,
由得:,
方程组的解是,
是方程组的解,
,
解得:,
故答案为:.
由于关于,的二元一次方程组可以变形为,若把看作,把看作,则方程组变成,则此时方程组的解为,即.
13.D
解:A、B、C均属于平移现象,不符合题意;而D属于旋转现象,符合题意.
故答案为:D.
风扇叶绕转轴旋转,是旋转现象.
14.5-2x
解:解:2x+y=5,
移项,得y=5-2x;
故答案为:5-2x.
根据用含x的代数式表示y,就要把方程中含有y的项移到方程的左边,其它的项移到方程的另一边求解即可.
15.9
解:∵m+2n﹣2=0,
∴m+2n=2,
∴3m 9n=3m (32)n=3m+2n=32=9,
故答案为:9.
将已知方程转化为m+2n=2;利用幂的乘方逆运算和同底数幂相乘的法则,将代数式转化为3m 9n=3m+2n,然后整体代入求值.
16.A
解:将x=1、y=1代入原方程得3-2m=1,解得m=1.
故答案为:A.
将解代入原方程即可解出.
17.C
解:平方差公式的形式为(a+b)(a-b)=a2-b2,观察四个选项,只有C符合题意,因为(2a-b)(2a+b)=4a2-b2.
故答案为:C.
根据平方差公式的形式判断各选项即可.
18.或或
19.;
20.C
解:根据题意易知∠FCD=45°,∠ABE=30°. 设AB与CF交点为H.
∵AB∥CD,
∴∠FHB=∠FCD=45°.
∴∠CGB=180°-∠FHB-∠ABE=180°-45°-30°=105°.
故答案为:C.
解题关键是通过平行知道∠FHB的度数.
21.2
解:,
①+②得3x+3y=6,即x+y=2.
故答案为:2.
通过观察方程组可知,上式加下式后将系数化为1即可.
22.C
解:数据比1小,故 0.00000209=2.09×10-6,
故答案为:C.
将较小的数化为一个数乘以10的负指数幂,这个数大于等1,小于10.
23.
解:设正方向DMNH的边长为a,正方形FGBE的边长为b,正方形HKEC的边长为c.
∵AB-BC=1,而AB=a+c,BC=b+c,
∴(a+c)-(b+c)=1,即a-b=1.
∵ S1+S2=8,
∴a2+b2=8.
∴(a-b)2+2ab=8,代入a-b=1得.
∴阴影部分面积.
故答案为:.
先设未知量a、b、c,阴影部分面积为ab,而根据条件,可先后推算出a-b、以及a2+b2的值,那么结合完全平方公式的变形,就能求出ab值.
24.A
解:由a||b知∠1=∠2,∠1=56°,故∠2=56°.
故答案为:A.
直接由两直线平行内错角相等求得结果.
25.B
解:穷举当x=1时,y=4;当x=2,y=1;而当x=3时,y=-2(不符合题意),只有2组结果.
故答案为:B.
直接对x、y进行穷举即可得到结果.
26.B
解:对于A,左右对称得到;对于B为平移得到;而C通过旋转得到;D则上下对称得到;
故答案为:B..
观察图形并想象前后是否能通过平移完全重合,能重合的即可平移得到。
27.14
解:根据题意,易知BE=2=AD,DF=AC=3,BE//AF.
∵∠ACB=90°,
∴BC⊥AF.
∴.
故答案为:14.
根据梯形面积的计算公式,已知高BC,则需要知道BE与AF的长,而这两条线段可以通过平移的性质计算出.
28.D
解:将方程组的解依次代入方程,对于A,3-4×(-2)=11,故不符合题意;对于B,-2≠3-1明显错误,不符合题意;对于C,3≠-2×2+5,不符合题意;对于D,-2×2-3×3=-13,符合题意.
故答案为:D .
依次将方程组的解代入选项中的方程中直接验证,即可得结果.
29.C
30.A
解:∵ , ,
∴ ,
即 ,
化简可得, .
故答案为:A.
由完全平方公式可得(a+b)2-(a-b)2=4ab,据此计算.
31.50
解:∵AB//CD
∴∠1=∠3
∵∠2=∠3
∴∠2=∠1=50°.
故答案为50.
如图,先由平行线的性质可得∠1=∠3,然后再根据对顶角相等可得∠2=∠3,即∠2=∠1=50°.
32.B
解:设正方形A的边长为a,正方形B的边长为b,
根据题意得,a(a+b) a2 b2=14,(a+b)2 a2 b2=36,
即ab b2=14,ab=18,
∴b2=18 14=4,
即正方形B的面积为4,
故答案为:B.
设正方形A的边长为a,正方形B的边长为b,用代数式表示图1、图2中阴影部分的面积,整体代入即可得出b2,即可得正方形B的面积.
33.B
解:A、∠1和∠2为对顶角,则本项不符合题意,
B、∠2和∠3为内错角,则本项符合题意,
C、∠1和∠3为同位角,则本项不符合题意,
D、∠2和∠4为同位角,则本项不符合题意,
故答案为:B.
根据内错角的定义:两条直线被第三条直线所截,如果两个角都在两条直线的内侧,并且在第三条直线的两侧,那么这样的一对角叫作内错角,据此逐项分析即可.
34.B
解:设一匹马价钱为x元,一头牛价钱为y元.
根据现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱可得:2x+y-10000=
一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱可得:10000-(x+2y)=
综上可得方程组:
故答案为:B.
首先认真读题,弄清题意,其次,根据题中所设的未知数x和y找出等量关系,然后根据现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱,列出方程组即可.
35.40°
解:如图,
∵AD||BC,
∴∠1=∠DAB=70°,
由折叠的性质知∠2=∠1=70°,
∴故∠CBF=180°-∠1-∠2=180°-70°-70°=40°,
故答案为:40°.
由二直线平行,内错角相等,可得∠1的度数,由折叠的性质可得∠1=∠2,进而根据平角定义即可求得∠CBF的度数.
36.
37.-1
解:.
故答案为:-1.
逆用积的乘方法则运算即可.
38.B
解:设B'F与EH的交点为K. 根据长方形的性质以及折叠,易知
A'E∥B'F,AD∥BC,∠ED'H=90°,∠BFE=∠EFB'.
∵∠EHD'=32°,
∴在Rt△D'EH中,∠D'EH=90°-32°=58°.
∵A'E∥B'F,AD∥BC,
∴∠D'EH=∠B'KH=∠B'FG=58°.
∴∠BFE=(180°-∠B'FG)÷2=(180°-58°)÷2=61°.
故答案为:B.
解题的关键是根据长方形的性质以及折叠的性质得A'E∥B'F,AD∥BC,∠ED'H=90°,∠BFE=∠EFB'.由直角三角形的性质求得∠D'EH,由平行线的性质得∠B'FG的度数,再由折叠和平角定义即可计算出∠B'FG.
39.
解:根据条件,即视x为已知量,y为未知量,则y=5-3x.
故答案为:5-3x.
把x看做已知数求出y即可.
1.(2024七下·杭州期中)计算:
2.(2024七下·临平期中)已知,用含的代数式表示,则 .
3.(2024七下·城厢期中)如图,将向右平移5个单位长度得到,且点B,E,C,F在同一条直线上,若,则的长度是 .
4.(2024七下·瑞安期中)端午节快到了,商店准备推出粽子礼盒,若3个粽子装一盒则装完还多2个礼盒,若2个粽子装一盒还多6个粽子.设有个礼盒,个粽子,所满足的关系式为( )
A. B.
C. D.
5.(2024七下·瑞安期中) 如图,与为同旁内角的是( )
A. B. C. D.
6.(2024·宿迁模拟)下列计算正确的是( )
A. B. C. D.
7.(2024七下·瑞安期中)碳纳米管,又名巴基管,是一种具有特殊结构的一维量子材料,其直径一般为厘米,其中用科学记数法表示为( )
A. B. C. D.
8.(2024七下·瑞安期中)下列计算正确的是( )
A. B.
C. D.
9.(2024七下·临平期中)若 ,则 .
10.(2024七下·临平期中)已知是二元一次方程的一组解,则 .
11.(2024七下·瑞安期中)已知,,则的值为( )
A.8 B.20 C.4 D.16
12.(2024七下·杭州期中)已知关于,的二元一次方程组的解为,则关于,的二元一次方程组的解为 .
13.(2024七下·瑞安期中)下列不属于平移现象的是( )
A.升降电梯上下移动 B.传送带上物品传输
C.拉抽屉 D.电风扇扇叶转动
14.(2024七下·杭州期中)已知方程,用含的代数式表示,则
15.(2024七下·成都期中)已知:m+2n﹣2=0,则3m 9n的值为 .
16.(2024七下·瑞安期中) 已知 是方程的一个解,则m的值为( )
A. B. C. D.
17.(2024七下·瑞安期中) 下列多项式相乘,可以用平方差公式计算的是( )
A. B.
C. D.
18.(2024七下·杭州期中)如图,两条平行直线,被直线所截,点位于两平行线之间,且在直线右侧,点是上一点,位于点右侧.小明进行了如下操作:连结,,在平分线上取一点,过点作,交直线于点.记,,,则 (用含,的代数式表示).
19.(2024七下·余杭期中)如图1,将一条两边互相平行的长方形纸带沿折叠,设度.
图1 图2
(1)若,则 度.
(2)将图1纸带继续沿折叠成图2,则 度.(用含的代数式表示)
20.(2024七下·瑞安期中) 将一副三角板按如图的方式摆放,已知,则的度数为( )
A. B. C. D.
21.(2024七下·瑞安期中) 已知方程组,则= .
22.(2024七下·新昌期中)芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000209kg,将0.00000209用科学记数法表示为( )
A. B.
C. D.
23.(2024七下·瑞安期中)如图,在长方形ABCD中,有正方形FGBE,正方形DMNH和正方形HKEC.S1,S2分别表示正方形FGBE,正方形DMNH的面积,若AB-BC=1,S1+S2=8,则阴影部分的面积是 .
24.(2024七下·新昌期中)如图,已知直线,直线c分别与直线a,b相交,
若∠1=56°,则∠2的度数为( )
A.56° B.34° C.114° D.124°
25.(2024七下·海淀期末)关于x,y的二元一次方程的正整数解的组数有( )
A.1组 B.2组 C.3组 D.4组
26.(2024七下·新昌期中)将下图中的叶子平移后,可以得到的图案是( )
A. B.
C. D.
27.(2024七下·瑞安期中) 如图,将直角三角形ABC平移2个单位得到直角三角形DEF,点A的对应点D落在AC上,已知,AC=3,BC=4,则梯形ABEF的面积是 .
28.(2024七下·新昌期中)已知二元一次方程组的解是,则括号内的方程可能是( )
A. B. C. D.
29.(2024七下·新昌期中)如图,下面四个条件中不能得到AB∥CD的是( )
A.∠B=∠1 B.∠A=∠2
C.∠B=∠BCD D.∠B+∠BCD=180°
30.(2024七下·新昌期中)已知 , ,则 的值为( )
A.1 B.2 C.4 D.
31.(2024七下·瑞安期中)如图,AB∥CD,∠1=50°,则∠2= °.
32.(2024七下·新昌期中)有两个正方形 ,将 并列放置后构造新的图形,分别得到长方形图甲与正方形图乙. 若图甲、图乙中阴影的面积分别为 14 与 36 ,则正方形 的面积为( )
A.3 B.4 C.5 D.6
33.(2024七下·开化期中)如图,在所标识的角中,内错角是( )
A.和 B.和 C.和 D.和
34.(2024七下·蒸湘期末)我国古代数学著作九章算术记载了一道“牛马问题”:“今有二马、一牛价过一万,如半马之价.一马、二牛价不满一万,如半牛之价.问牛、马价各几何.”其大意为:现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱,求一匹马、一头牛各多少钱?设一匹马价钱为元,一头牛价钱为元,则符合题意的方程组是( )
A.
B.
C.
D.
35.(2024七下·杭州期中)如图,将一条长方形纸片沿AB折叠,已知∠DAB=70°,则∠CBF= .
36.(2024七下·杭州期中)如图,将三角形平移得到三角形,若图中阴影部分面积与所有空白部分面积之比为,则阴影部分面积与三角形面积的比值为 .
37.(2024七下·瑞安期中) 计算:= .
38.(2024七下·瑞安期中)如图,把长方形纸条沿EF,GH折叠(点E,H在AD 边上,点F,G在BC边上),A点的对称点为点,D点的对称点为点,若线段落在边E上,∠EH=32°,则∠BFE等于( )
A.58° B.61° C.62° D.64°
39.(2024七下·瑞安期中) 已知方程,用关于的代数式表示,则= .
答案解析部分
1.6a3b
解:2a2b 3a=6a3b.
故答案为:6a3b.
根据单项式与单项式相乘,把他们的系数,相同字母的幂分别相乘,对于只在某一个单项式含有的字母则连同指数作为积的一个因式,计算即可.
2.5b+2
解:由等式的性质得a=2+5b
故答案为:5b+2.
直接由等式的性质进行移项便可得结果.
3.8
4.A
解:根据条件“ 若3个粽子装一盒则装完还多2个礼盒 ”,即用(x-2)个礼盒,每个礼盒装3个粽子刚好装完y个粽子,于是有3(x-2)=y;根据条件“ 若2个粽子装一盒还多6个粽子 ”,即用x个礼盒,每个礼盒装2个粽子下,还剩6个粽子,于是有2x+6=y.
因此,得到二元一次方程组.
故答案为:A.
要抓住等量关系的重点,即不论哪种包装方式,粽子的数量保持不变.
5.D
解:根据图片,∠5的同旁内角为∠4.
故答案为:D.
同旁内角的定义: 两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角.
6.D
解:对A,正确结果应为m5; 对于B,正确结果应为9m2; 对于C,正确结果应为m4;D正确;
故答案为:D.
根据同底数幂的乘法、除法、乘方的规则进行一 一判断即可.
7.B
解:当小数点向右移动到4后时,共移动7位,故为4.0x10-7.
故答案为:B.
科学记数法表示大于0小于1的数:ax10n,其中1≤a<10,且n为负整数,为小数点向右移动到第1个非零数后面时,小数点移动的位数.
8.C
解:A、,A错误;
B、a3+a4无法合并同类项,B错误;
C、计算无误,C正确;
D、,D错误.
故答案为:C.
根据同底数幂的乘除法、合并同类项法则、积的乘方法则等逐一检验各选项即可.
9.-2
解:∵(x+3)(x 5)= x2 5x+3x 15=x2 2x 15,
∴m= 2.
故答案为: 2.
根据多项式与多项式的乘法法则将左式展开并合并同类项,然后根据多项式的性质可得m的值.
10.2023
解:将x=1,y=-1代入方程可得2a-b=-1,于是2a-b+2024=-1+2024=2023
故答案为:2023.
将解代入方程再进行整体代换可得结果.
11.C
解:∵,,
∴
∴.
故答案为:C.
解题关键是结合完全平方公式先计算出的值.
12.
解:由,得:
,
设,
由得:,
方程组的解是,
是方程组的解,
,
解得:,
故答案为:.
由于关于,的二元一次方程组可以变形为,若把看作,把看作,则方程组变成,则此时方程组的解为,即.
13.D
解:A、B、C均属于平移现象,不符合题意;而D属于旋转现象,符合题意.
故答案为:D.
风扇叶绕转轴旋转,是旋转现象.
14.5-2x
解:解:2x+y=5,
移项,得y=5-2x;
故答案为:5-2x.
根据用含x的代数式表示y,就要把方程中含有y的项移到方程的左边,其它的项移到方程的另一边求解即可.
15.9
解:∵m+2n﹣2=0,
∴m+2n=2,
∴3m 9n=3m (32)n=3m+2n=32=9,
故答案为:9.
将已知方程转化为m+2n=2;利用幂的乘方逆运算和同底数幂相乘的法则,将代数式转化为3m 9n=3m+2n,然后整体代入求值.
16.A
解:将x=1、y=1代入原方程得3-2m=1,解得m=1.
故答案为:A.
将解代入原方程即可解出.
17.C
解:平方差公式的形式为(a+b)(a-b)=a2-b2,观察四个选项,只有C符合题意,因为(2a-b)(2a+b)=4a2-b2.
故答案为:C.
根据平方差公式的形式判断各选项即可.
18.或或
19.;
20.C
解:根据题意易知∠FCD=45°,∠ABE=30°. 设AB与CF交点为H.
∵AB∥CD,
∴∠FHB=∠FCD=45°.
∴∠CGB=180°-∠FHB-∠ABE=180°-45°-30°=105°.
故答案为:C.
解题关键是通过平行知道∠FHB的度数.
21.2
解:,
①+②得3x+3y=6,即x+y=2.
故答案为:2.
通过观察方程组可知,上式加下式后将系数化为1即可.
22.C
解:数据比1小,故 0.00000209=2.09×10-6,
故答案为:C.
将较小的数化为一个数乘以10的负指数幂,这个数大于等1,小于10.
23.
解:设正方向DMNH的边长为a,正方形FGBE的边长为b,正方形HKEC的边长为c.
∵AB-BC=1,而AB=a+c,BC=b+c,
∴(a+c)-(b+c)=1,即a-b=1.
∵ S1+S2=8,
∴a2+b2=8.
∴(a-b)2+2ab=8,代入a-b=1得.
∴阴影部分面积.
故答案为:.
先设未知量a、b、c,阴影部分面积为ab,而根据条件,可先后推算出a-b、以及a2+b2的值,那么结合完全平方公式的变形,就能求出ab值.
24.A
解:由a||b知∠1=∠2,∠1=56°,故∠2=56°.
故答案为:A.
直接由两直线平行内错角相等求得结果.
25.B
解:穷举当x=1时,y=4;当x=2,y=1;而当x=3时,y=-2(不符合题意),只有2组结果.
故答案为:B.
直接对x、y进行穷举即可得到结果.
26.B
解:对于A,左右对称得到;对于B为平移得到;而C通过旋转得到;D则上下对称得到;
故答案为:B..
观察图形并想象前后是否能通过平移完全重合,能重合的即可平移得到。
27.14
解:根据题意,易知BE=2=AD,DF=AC=3,BE//AF.
∵∠ACB=90°,
∴BC⊥AF.
∴.
故答案为:14.
根据梯形面积的计算公式,已知高BC,则需要知道BE与AF的长,而这两条线段可以通过平移的性质计算出.
28.D
解:将方程组的解依次代入方程,对于A,3-4×(-2)=11,故不符合题意;对于B,-2≠3-1明显错误,不符合题意;对于C,3≠-2×2+5,不符合题意;对于D,-2×2-3×3=-13,符合题意.
故答案为:D .
依次将方程组的解代入选项中的方程中直接验证,即可得结果.
29.C
30.A
解:∵ , ,
∴ ,
即 ,
化简可得, .
故答案为:A.
由完全平方公式可得(a+b)2-(a-b)2=4ab,据此计算.
31.50
解:∵AB//CD
∴∠1=∠3
∵∠2=∠3
∴∠2=∠1=50°.
故答案为50.
如图,先由平行线的性质可得∠1=∠3,然后再根据对顶角相等可得∠2=∠3,即∠2=∠1=50°.
32.B
解:设正方形A的边长为a,正方形B的边长为b,
根据题意得,a(a+b) a2 b2=14,(a+b)2 a2 b2=36,
即ab b2=14,ab=18,
∴b2=18 14=4,
即正方形B的面积为4,
故答案为:B.
设正方形A的边长为a,正方形B的边长为b,用代数式表示图1、图2中阴影部分的面积,整体代入即可得出b2,即可得正方形B的面积.
33.B
解:A、∠1和∠2为对顶角,则本项不符合题意,
B、∠2和∠3为内错角,则本项符合题意,
C、∠1和∠3为同位角,则本项不符合题意,
D、∠2和∠4为同位角,则本项不符合题意,
故答案为:B.
根据内错角的定义:两条直线被第三条直线所截,如果两个角都在两条直线的内侧,并且在第三条直线的两侧,那么这样的一对角叫作内错角,据此逐项分析即可.
34.B
解:设一匹马价钱为x元,一头牛价钱为y元.
根据现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱可得:2x+y-10000=
一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱可得:10000-(x+2y)=
综上可得方程组:
故答案为:B.
首先认真读题,弄清题意,其次,根据题中所设的未知数x和y找出等量关系,然后根据现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱,列出方程组即可.
35.40°
解:如图,
∵AD||BC,
∴∠1=∠DAB=70°,
由折叠的性质知∠2=∠1=70°,
∴故∠CBF=180°-∠1-∠2=180°-70°-70°=40°,
故答案为:40°.
由二直线平行,内错角相等,可得∠1的度数,由折叠的性质可得∠1=∠2,进而根据平角定义即可求得∠CBF的度数.
36.
37.-1
解:.
故答案为:-1.
逆用积的乘方法则运算即可.
38.B
解:设B'F与EH的交点为K. 根据长方形的性质以及折叠,易知
A'E∥B'F,AD∥BC,∠ED'H=90°,∠BFE=∠EFB'.
∵∠EHD'=32°,
∴在Rt△D'EH中,∠D'EH=90°-32°=58°.
∵A'E∥B'F,AD∥BC,
∴∠D'EH=∠B'KH=∠B'FG=58°.
∴∠BFE=(180°-∠B'FG)÷2=(180°-58°)÷2=61°.
故答案为:B.
解题的关键是根据长方形的性质以及折叠的性质得A'E∥B'F,AD∥BC,∠ED'H=90°,∠BFE=∠EFB'.由直角三角形的性质求得∠D'EH,由平行线的性质得∠B'FG的度数,再由折叠和平角定义即可计算出∠B'FG.
39.
解:根据条件,即视x为已知量,y为未知量,则y=5-3x.
故答案为:5-3x.
把x看做已知数求出y即可.
同课章节目录
