2024-2025学年浙教版七年级数学下册期中真题专项复习07填空题(含答案)(浙江专用)
文档属性
| 名称 | 2024-2025学年浙教版七年级数学下册期中真题专项复习07填空题(含答案)(浙江专用) |  | |
| 格式 | docx | ||
| 文件大小 | 509.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 21:36:19 | ||
图片预览



文档简介
2024-2025学年七年级数学下册期中真题专项复习07填空题
1.(2024七下·浦江期中)若是方程 2x-y=2的一个解,则6a-3b+1 =
2.(2024七下·海曙期中)计算: .
3.(2024·七下婺城期中)已知是方程的一个解,则m的值为 .
4.(2024七下·杭州期中)已知,则的值为 .
5.(2024·七下婺城期中)若实数m、n满足,则= .
6.(2024七下·金东期中) 如图,已知长方形纸片,点在边上,点在边上,分别沿折叠,使点B和点C都落在点P处,若,则的度数为 .
7.(2024七下·海曙期中)关于,的方程组与有相同的解,则 .
8.(2024七下·浦江期中)如图所示,请你添加一个条件(图中不得添加另外标记) ,使得AB ∥ DE
9.(2024七下·海曙期中)计算: .
10.(2024七下·金东期中) 图1是一款落地的平板支撑架,,是可转动的支撑杆。调整支撑杆使得其侧面示意图如图2所示,此时平板,,,则 °;现将支撑杆调整至图3所示位置,调整过程中,大小不变,,再顺时针调整平板至,使得,则 °.
11.(2024七下·温州期中) 将方程写成用含x的代数式表示y的形式 .
12.(2024七下·滨江期中)已知方程2x+y=7,用关于x的代数式表示y得:y= .
13.(2024七下·海曙期中)已知 ,则 .
14.(2024七下·浦江期中)已知2x+3y-3=0,则4x·8y=
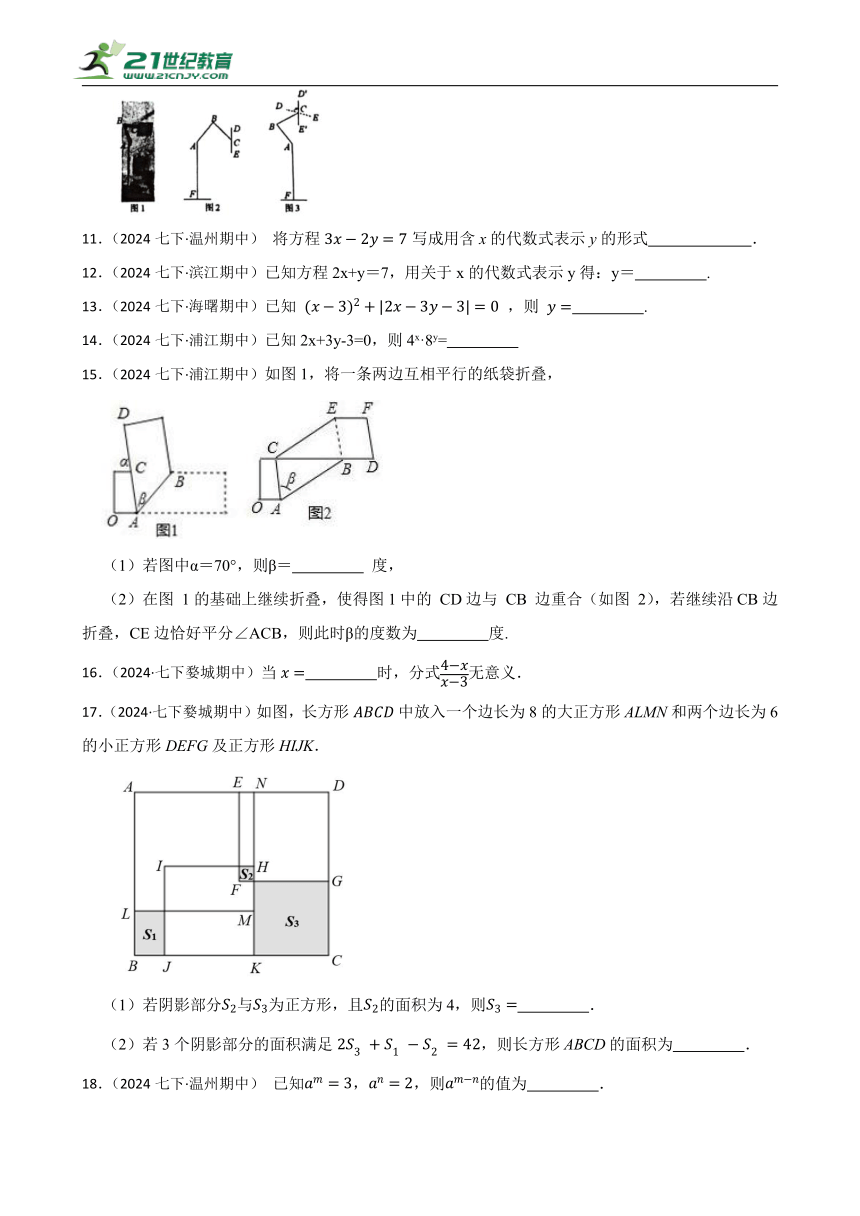
15.(2024七下·浦江期中)如图1,将一条两边互相平行的纸袋折叠,
(1)若图中α=70°,则β= 度,
(2)在图 1的基础上继续折叠,使得图1中的 CD边与 CB 边重合(如图 2),若继续沿CB边折叠,CE边恰好平分∠ACB,则此时β的度数为 度.
16.(2024·七下婺城期中)当 时,分式无意义.
17.(2024·七下婺城期中)如图,长方形中放入一个边长为8的大正方形ALMN和两个边长为6的小正方形DEFG及正方形HIJK.
(1)若阴影部分与为正方形,且的面积为4,则 .
(2)若3个阴影部分的面积满足,则长方形ABCD的面积为 .
18.(2024七下·温州期中) 已知,,则的值为 .
19.(2024七下·滨江期中)如图,已知,∠1=100°,则∠2= 度.
20.(2024七下·温州期中) 图1是光伏发电场景,其示意图如图2,为吸热塔,在地平线上的点C,D处各安装定日镜(介绍见图3).绕各中心点(A,B)旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点O处.A、B处于同一水平高度,已知反射光线与水平线的夹角是,镜面与立杆的夹角,则太阳光线与水平面夹角 ;若反射光线与水平线的夹角是时,则 .
21.(2024七下·金东期中) 已知正方形的面积为9x2+30xy+25y2(x>0,y>0),利用因式分解,可以求出正方形的边长为 .
22.(2024七下·温州期中)若关于x、y的二元一次方程组的解为,则方程组的解为 .
23.(2024七下·杭州期中)计算 .
24.(2024七下·浦江期中)若x-2y=0,则分式 的值
25.(2024七下·海曙期中)已知方程,用含的代数式表示,则 .
26.(2024七下·海曙期中)如图,直线分别与直线,相交于点,,平分∠BEF,交直线于点,若∠MFD=∠BEF=64°,作射线于点,则∠PGF的度数为 度。
27.(2024七下·遂宁期中)若关于x、y的二元一次方程组的解是,则关于a、b的二元一次方程组 的解是 .
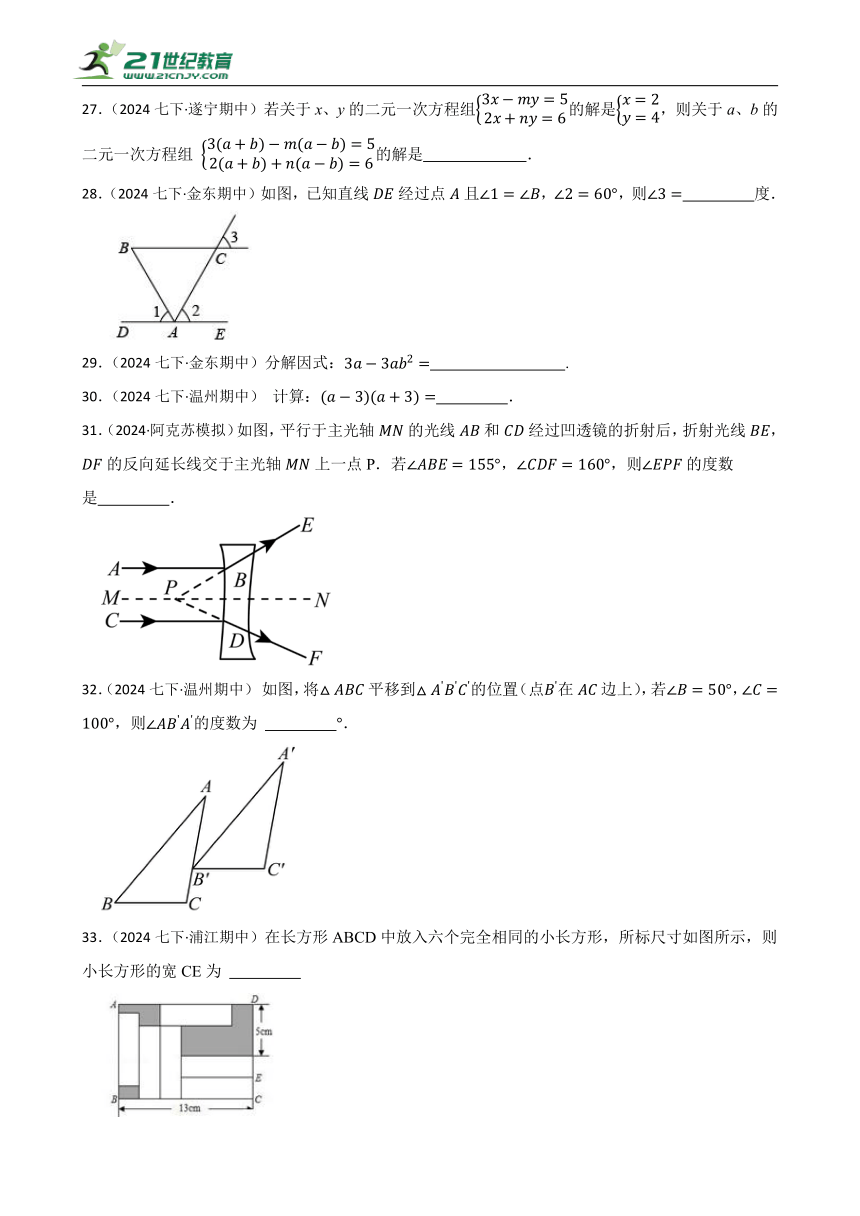
28.(2024七下·金东期中)如图,已知直线经过点且,,则 度.
29.(2024七下·金东期中)分解因式: .
30.(2024七下·温州期中) 计算: .
31.(2024·阿克苏模拟)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点P.若,,则的度数是 .
32.(2024七下·温州期中) 如图,将平移到的位置(点在边上),若,,则的度数为 .
33.(2024七下·浦江期中)在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为
34.(2024七下·泗阳期末)分解因式: = .
35.(2024七下·杭州期中)如图所示,把一块三角尺的直角顶点放在直尺的一边上,如果,则 .
36.(2024七下·海曙期中)如果展开后的结果中不含的一次项,那么 .
37.(2024七下·滨江期中)如图,点A,B在数轴上所对应的数分别为﹣3和,且点A,B到原点的距离相等,则a的值为 .
38.(2024七下·滨江期中)甲、乙两个大小不一样的正方形按如图所示的两种方式放置AB=a,CD=b,记图①中的阴影部分面积为.图②中的阴影部分面积为,甲正方形的面积为.
(1)若,则的值是 ;
(2)若,则的值是 .
39.(2024七下·海曙期中)如图,在中,,AC=5,将沿向右平移得到,若平移距离为2.5,则四边形的面积等于 .
40.(2024七下·杭州期中)如图,直线,点A在直线与之间,点B在直线上,连接,的平分线交于点C,连结,过点A作交于点D,作交于点F,平分交于点E.若,,则的度数为 .
41.(2024七下·滨江期中)因式分解: .
42.(2024九下·武威模拟)已知m+n=mn,则(m-1)(n-1)= .
43.(2024七下·杭州期中)已知,,则 .
44.(2024七下·金东期中)
(1)如果,则 .
(2) .
45.(2024七下·温州期中) 若是关于x,y的二元一次方程的一个解,则k的值为 .
46.(2024七下·滨江期中)如图,在△ABC中,∠ABC=90°,∠CAB=35°,D是线段AB上的一个动点,连结CD,将△CDB沿着CD翻折,得到△CDE,当△CDE的三边与△ABC的三边至少有一组边平行时,∠CDB的度数是 .
答案解析部分
1.7
解:∵是方程 2x-y=2的一个解,
∴2a-b=2,
∴ 6a-3b+1 = 3(2a-b)+1=3×2+1=7.
故答案为:7.
先代入解得到关于a和b的等式,再代入求值即可.
2.8
解:原式=1-1+8=8.
故答案为:8.
利用零指数幂、乘方及负整数指数幂先计算,再计算加减即可.
3.2
解:将 代入方程2x+3y=1,可得2m-3=1,
∴ m=2.
故答案为:2.
将二元一次方程的解代入方程,即可求得.
4.2025
解:(a-1)(b-1)=ab-a-b+1,
∵ ab=a+b+2024,
∴ ab-a-b=2024,
∴ 原式=2024+1=2025.
故答案为:2025.
根据整式的乘法变形后,再将ab-a-b=2024代入,即可求得.
5.
解:
∴ m=-3,n=2,
∴ nm=2-3=.
故答案为: .
根据多项式乘多项式的法则计算后,各项的系数相同,求得m和n的值,再计算nm即可.
6.
解:四边形是长方形,
,
由折叠的性质得:,
,
,
,
,
,
,
,
故答案为:.
先根据矩形的性质可得,再根据折叠的性质可得,,然后根据邻补角的定义可得,最后根据三角形的内角和定理可得,由此即可得出答案.
7.-2
解:联立方程组得:,解得,
把代入4ax+5by=-28,ax-by=8中
得:,解得,
∴a-b==-2.
故答案为:-2.
联立不含a、b的方程为方程组并解之,求出xy的值,再建立关于a、b的方程组,解之即得a、b的值,再代入计算即可.
8.∠ABD=∠BDE(或∠ABE=∠DEC或∠ABE+∠BED=180°)
9.4x2 -6
解:原式=4x3÷x-6x÷x=4x2 -6.
故答案为:4x2 -6.
利用多项式除以单项式法则进行计算即可.
10.43;75
解:如图,过点B作,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴;
如图,延长,交于点H,
由上述可知,,
∵,,
∴,
∵,
∴,
∴,
∴.
故答案为:43,75.
在图2中,过点B作,易得,由平行线的性质:两直线平行,同旁内角互补可得,进而可得,以此求得,由平行线的性质即可得到;在图3中,延长,交于点H,由上述可求出,由三角形外角性质可得,再利用平行线的性质得到,则.
11.
12.﹣2x+7
解:方程2x+y=7,
解得:y=﹣2x+7.
故答案为:-2x+7.
将不含y的项移至右边即可.
13.1
解:根据题意得, ,
由 得, ,
把 代入 得, ,
解得 .
故答案为:1.
根据偶次幂及绝对值的非负性,由两个非负数的和为0,则每一个数都等于0,可得,解之即可.
14.8
解:∵ 2x+3y-3=0,
∴2x+3y=3
∴ 4x·8y=22x·23y=22x+3y=23=8.
故答案为:8.
根据等式得2x+3y=3,再利用积的乘方和幂的乘方的逆运算进行计算即可
15.(1)55
(2)45
解: (1)根据上下边互相平行可知,∠a=∠OAD,
∵a=70°,
∴∠OAD=70°.
又∵∠OAD+ 2β=180°,
∴β= 55°.
故答案为:55.
( 2 )根据折叠的性质可知,折叠两次后形成的三个角都相等,
根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为1 80°,故每个角为45°,
∴∠ACB=90°,即a=90°,
由(1)中可得,β=.
故答案为:45.
( 1 )根据两直线平行,同位角相等,可知∠OAD=α=70°,再利用折叠的性质可知∠OAD+ 2β=180°,如此即可求出β的值;
( 2 )根据折叠的性质可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,从而可知∠ACB=90°,再由(1)的思路可得β的值.
16.3
解:根据题意得,分母x-3为0时,分式无意义,
∴ x=3时,分式 无意义.
故答案为:3.
根据分式无意义的条件,即可求得.
17.(1)16
(2)130
解:(1)∵ S2=4,S2为正方形,
∴ S2的边长为2,
∵ FG=6,
∴ S3的边长为4,
∴ S3的面积为16;
(2)设长方形的长AD=a,宽AB=b,
则S3的面积为(a-8)(a-6),S1面积为2(b-8),S2的面积为(12-b)(14-a),
即2(a-8)(a-6)+2(b-8)-(12-b)(14-a)=42,
化简可得,ab=130.
故答案为:(1)16;(2)130.
(1)根据正方形的面积公式可得S2的边长,根据S3的边长求得其面积;
(2)设长方形的长AD=a,宽AB=b,分别用a和b表示出三个阴影面积,代入关系式计算即可求得ab的值,即为所求.
18.
解:
故答案为:.
根据同底数幂的除法法则计算即可.
19.80
解:如图所示,
∵ a∥b
∴∠1=∠3=100°
∵ ∠2+∠3=180°
∴ ∠2=80°
故答案为:80.
本题考查平行线的性质及邻补角,熟悉平行线的性质是解题关键。由 a∥b得∠1=∠3=100°
根据 ∠2+∠3=180°得 ∠2=80°.
20.65;53
解:如图:分别作出两个定日镜的法线:
∵反射光线与水平线的夹角是,镜面与立杆的夹角
∴
∵
∴
∴
∵光线是平行的
∴
∵反射光线与水平线的夹角是时
∴
∵
∴
则
∵
∴
故答案为:65,53
根据题意的新定义内容,作出法线,依据垂直的定义,结合已知角,得出,再利用角的运算,得出,结合光线是平行的,得出,结合已知角以及角的和差关系列式代入数值,进行计算,即可作答.
21.3x+5y
解:9x2+30xy+25y2=(3x+5y)2,
所以该正方形的边长为(3x+5y).
故答案为:(3x+5y).
将已知正方形的面积利用完全平方公式分解因式后,即可得出正方形的边长.
22.
解:∵
∴
∵关于x、y的二元一次方程组的解为
∴
解得
故答案为:
先整理得,结合换元思想即可得出,即可求解.
23.
解:
设,
原式=a(b+)-b(a-)=ab+-ab+=,
∵ a+b=1,
∴ 原式=.
故答案为:.
设,将原式化简后,再计算a+b,即可求得.
24.
解:∵ x-2y=0,
∴x=2y
∴
故答案为:.
由x-2y=0得x=2y,再代入分式求解即可.
25.5-3x
解:,
移项得:y=5-3x.
把含x项移到方程右边即可.
26.58或122
解:∵ ∠MFD=∠BEF=64°,
∴CD∥AB,
∴∠FGE=∠GEB,
∵平分∠BEF,
∴∠FEG=∠GEB=∠BEF=32°,
∴∠FGE=∠FEG=32°,
当GP在EG的上方时, 且,
∴∠PGF=∠PGE-∠FGE=90°-32°=58°,
当GP在EG的下方时, 且,
∠PGF=∠PGE+∠FGE=90°+32°=122°,
综上可知: ∠PGF的度数为58或122度.
故答案为:58或122.
先推出CD∥AB,利用平行线的性质及角平分线的定义可得∠FGE=∠FEG=32°,由,可分两种情况:当GP在EG的上方时和GP在EG的下方时,利用角的和差关系分别求解即可.
27.
解:∵的解是,
∴ 的解是
∴ .
故答案为: .
根据二元一次方程组 与 同解可得再解二元一次方程组即可求得.
28.60
解:,
,
,
故答案为:60.
根据平行线的判定及性质,即可解答.
29.
解:;
故答案为:.
观察此多项式的特点:含有公因式3a,因此先提取公因式,再利用公式法分解因式.
30.
解:
故答案为:
根据平方差公式计算即可.
31.
∵,
∴,.
∵,
∴,
同理,,
∴.
故答案为:.
先根据平角的定义分别求出,再根据平行线的性质求出,同理可得,而∠EPF=∠BPN+∠DPN,即可求得.
32.30
解:∵,,
∴,
∵平移得到,
∴,
∴,
故答案为:.
由三角形内角和定理可得,由平移可得,再根据平行线的性质即可求解.
33.2
解:设小长方形的宽为xcm,长为ycm,根据题意得:
解得:,
则小长方形的宽为2cm.
故答案为:2.
根据题意,设小长方形的宽为xcm,长为ycm,根据图形中的数量关系列出方程,求出方程的解,即可得出答案.
34.x(x﹣1)
=x(x﹣1).
故答案为:x(x﹣1).
观察此多项式的特点:含有公因式x,由此利用提公因式法分解因式。
35.62°或62度
解:如图,
∵ 直尺的上下边平行,
∴ ∠2=∠3,
∵ ∠ABC=90°,
∴ ∠1+∠3=90°,
∴ ∠1+∠2=90°,
∵ ∠1=28°,
∴ ∠2=62°.
故答案为:62°或62度.
根据平行线的性质可得∠2=∠3,再利用∠1与∠3互余,即可求得.
36.14
解:=2x2+(m-14)x-7m,
∵ 原式展开后的结果中不含的一次项,
∴m-14=0,
解得m=14.
故答案为:14.
利用多项式乘多项式将原式展开,由原式展开后的结果中不含的一次项, 可得m-14=0,解之即可.
37.3
解:由数轴可知,点A表示的数为-3,则点B表示的数为,且>0
∵ 点A,B到原点的距离相等,
∴=
∴ a=3a-6
解得:a=3
故答案为:3.
本题考查绝对值,熟练掌握绝对值的知识是解题关键。由数轴可知,点A表示的数为-3,则点B表示的数为,根据点A,B到原点的距离相等可得=,求解可得a.
38.(1)0
(2)4
解:(1)由图形摆放可知,正方形甲的边长为a, =a2,正方形乙的边长为a-b, 图①中的阴影部分面积为 =2a(a-b), 图②中的阴影部分面积为 =a2-(a-b)2,
∵
∴ 2a(a-b)+a2-(a-b)2=a2
整理得:a2-2b2=0
∴
故答案为:0.
(2)∵
∴ 2a(a-b)=a2-(a-b)2,
整理得:2a2+b2=4ab
∴
本题考查整式的应用及分式的化简,应用整体代入的思想求值是解题关键。根据图形,列出 =a2, =2a(a-b), =a2-(a-b)2,(1)根据,化简得a2-2b2=0,得;(2)由得2a2+b2=4ab,则.
39.12.5
解:由平移知:AD=BE=2.5,AD∥BE,
∴四边形ABED是平行四边形,
∴ 四边形的面积为BE·AC=2.5×5=12.5.
故答案为:12.5.
利用平移的性质可推出四边形ABED是平行四边形,BE=2.5,根据平行四边形的面积公式进行计算即可.
40.54°
解:
∵AE平分∠DAF,
∴设∠EAF=∠DAE=x,
又∵AD⊥PQ,,,
∴∠AFD=90°-∠DAF=90°-2x,∠ACB=,∠ACD=90°-∠CAE-∠DAE=45°-x,
∴∠BCQ=∠ACB+∠ACD=+(45°-x)=,
又∵AB∥PQ,
∴∠MBC=∠BCQ=,
又∵BC平分∠ABM,
∴∠ABM=2∠MBC=3x+90°,
∴∠ABN=180°-∠ABM=90°-3x,
如图,过点A作AG∥MN,
∵MN∥PQ,
∴AG∥PQ,
∴∠BAG=∠ABN=90°-3x,∠FAG=∠AFD=90°-2x,
又∵AB⊥AF,
∴∠BAF=∠ABN+∠AFD=(90°-3x)+(90°-2x)=90°,解得x=18°,
∴∠AFD=90°-2x=90°-36°=54°,
故填:54°.
由已知条件的角度关系,根据角度较小且含多个角度直接关联,可直接设∠EAF=∠DAE=x,利用已知条件信息及平行线的性质逐一表示各个角度,为求出目标角的度数,在表示的基础上进一步利用“猪蹄模型”得出等量关系解之即可.
41.m(m+1)(m﹣1)
解:原式=m(m2﹣12)
=m(m+1)(m﹣1).
故答案为:m(m+1)(m﹣1).
利用提公因式法与公式法计算即可。
42.1
根据乘法公式多项式乘以多项式,用第一个多项式的每一项乘以第二个多项式的每一项,可求 (m-1)(n-1) = mn-m-n+1=mn-(m+n)+1,直接代入m+n=mn可求得 (m-1)(n-1) = 1.
利用多项式乘以多项式的法则可算出答案。
43.30
解:∵,,
∴;
故答案为:30.
直接用同底数幂相乘计算即可.
44.(1)5
(2)
45.2
解:把代入
得:
解得:.
故答案为:2
将方程的解代入方程即可求出参数k的值.
46.45°
解:如图,点D在线段AB上时,DE∥BC
∴ ∠EDC=∠BCD
由折叠知:∠EDC=∠CDB,∠ECD=∠BCD
∴ ∠EDC=∠BCD=∠CDB=∠ECD
∵ ∠ABC=90°
∴ ∠CDB=∠EDC=∠BCD=∠ECD=45°,此时EC∥BD
∴ ∠CDB=45°
故答案为:45°.
本题考查折叠的性质,平行线的性质,掌握折叠的性质和平行线的性质是解题关键。由DE∥BC得∠EDC=∠BCD,根据折叠得∠EDC=∠CDB,∠ECD=∠BCD,可得 ∠CDB=45°.
1.(2024七下·浦江期中)若是方程 2x-y=2的一个解,则6a-3b+1 =
2.(2024七下·海曙期中)计算: .
3.(2024·七下婺城期中)已知是方程的一个解,则m的值为 .
4.(2024七下·杭州期中)已知,则的值为 .
5.(2024·七下婺城期中)若实数m、n满足,则= .
6.(2024七下·金东期中) 如图,已知长方形纸片,点在边上,点在边上,分别沿折叠,使点B和点C都落在点P处,若,则的度数为 .
7.(2024七下·海曙期中)关于,的方程组与有相同的解,则 .
8.(2024七下·浦江期中)如图所示,请你添加一个条件(图中不得添加另外标记) ,使得AB ∥ DE
9.(2024七下·海曙期中)计算: .
10.(2024七下·金东期中) 图1是一款落地的平板支撑架,,是可转动的支撑杆。调整支撑杆使得其侧面示意图如图2所示,此时平板,,,则 °;现将支撑杆调整至图3所示位置,调整过程中,大小不变,,再顺时针调整平板至,使得,则 °.
11.(2024七下·温州期中) 将方程写成用含x的代数式表示y的形式 .
12.(2024七下·滨江期中)已知方程2x+y=7,用关于x的代数式表示y得:y= .
13.(2024七下·海曙期中)已知 ,则 .
14.(2024七下·浦江期中)已知2x+3y-3=0,则4x·8y=
15.(2024七下·浦江期中)如图1,将一条两边互相平行的纸袋折叠,
(1)若图中α=70°,则β= 度,
(2)在图 1的基础上继续折叠,使得图1中的 CD边与 CB 边重合(如图 2),若继续沿CB边折叠,CE边恰好平分∠ACB,则此时β的度数为 度.
16.(2024·七下婺城期中)当 时,分式无意义.
17.(2024·七下婺城期中)如图,长方形中放入一个边长为8的大正方形ALMN和两个边长为6的小正方形DEFG及正方形HIJK.
(1)若阴影部分与为正方形,且的面积为4,则 .
(2)若3个阴影部分的面积满足,则长方形ABCD的面积为 .
18.(2024七下·温州期中) 已知,,则的值为 .
19.(2024七下·滨江期中)如图,已知,∠1=100°,则∠2= 度.
20.(2024七下·温州期中) 图1是光伏发电场景,其示意图如图2,为吸热塔,在地平线上的点C,D处各安装定日镜(介绍见图3).绕各中心点(A,B)旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点O处.A、B处于同一水平高度,已知反射光线与水平线的夹角是,镜面与立杆的夹角,则太阳光线与水平面夹角 ;若反射光线与水平线的夹角是时,则 .
21.(2024七下·金东期中) 已知正方形的面积为9x2+30xy+25y2(x>0,y>0),利用因式分解,可以求出正方形的边长为 .
22.(2024七下·温州期中)若关于x、y的二元一次方程组的解为,则方程组的解为 .
23.(2024七下·杭州期中)计算 .
24.(2024七下·浦江期中)若x-2y=0,则分式 的值
25.(2024七下·海曙期中)已知方程,用含的代数式表示,则 .
26.(2024七下·海曙期中)如图,直线分别与直线,相交于点,,平分∠BEF,交直线于点,若∠MFD=∠BEF=64°,作射线于点,则∠PGF的度数为 度。
27.(2024七下·遂宁期中)若关于x、y的二元一次方程组的解是,则关于a、b的二元一次方程组 的解是 .
28.(2024七下·金东期中)如图,已知直线经过点且,,则 度.
29.(2024七下·金东期中)分解因式: .
30.(2024七下·温州期中) 计算: .
31.(2024·阿克苏模拟)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点P.若,,则的度数是 .
32.(2024七下·温州期中) 如图,将平移到的位置(点在边上),若,,则的度数为 .
33.(2024七下·浦江期中)在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为
34.(2024七下·泗阳期末)分解因式: = .
35.(2024七下·杭州期中)如图所示,把一块三角尺的直角顶点放在直尺的一边上,如果,则 .
36.(2024七下·海曙期中)如果展开后的结果中不含的一次项,那么 .
37.(2024七下·滨江期中)如图,点A,B在数轴上所对应的数分别为﹣3和,且点A,B到原点的距离相等,则a的值为 .
38.(2024七下·滨江期中)甲、乙两个大小不一样的正方形按如图所示的两种方式放置AB=a,CD=b,记图①中的阴影部分面积为.图②中的阴影部分面积为,甲正方形的面积为.
(1)若,则的值是 ;
(2)若,则的值是 .
39.(2024七下·海曙期中)如图,在中,,AC=5,将沿向右平移得到,若平移距离为2.5,则四边形的面积等于 .
40.(2024七下·杭州期中)如图,直线,点A在直线与之间,点B在直线上,连接,的平分线交于点C,连结,过点A作交于点D,作交于点F,平分交于点E.若,,则的度数为 .
41.(2024七下·滨江期中)因式分解: .
42.(2024九下·武威模拟)已知m+n=mn,则(m-1)(n-1)= .
43.(2024七下·杭州期中)已知,,则 .
44.(2024七下·金东期中)
(1)如果,则 .
(2) .
45.(2024七下·温州期中) 若是关于x,y的二元一次方程的一个解,则k的值为 .
46.(2024七下·滨江期中)如图,在△ABC中,∠ABC=90°,∠CAB=35°,D是线段AB上的一个动点,连结CD,将△CDB沿着CD翻折,得到△CDE,当△CDE的三边与△ABC的三边至少有一组边平行时,∠CDB的度数是 .
答案解析部分
1.7
解:∵是方程 2x-y=2的一个解,
∴2a-b=2,
∴ 6a-3b+1 = 3(2a-b)+1=3×2+1=7.
故答案为:7.
先代入解得到关于a和b的等式,再代入求值即可.
2.8
解:原式=1-1+8=8.
故答案为:8.
利用零指数幂、乘方及负整数指数幂先计算,再计算加减即可.
3.2
解:将 代入方程2x+3y=1,可得2m-3=1,
∴ m=2.
故答案为:2.
将二元一次方程的解代入方程,即可求得.
4.2025
解:(a-1)(b-1)=ab-a-b+1,
∵ ab=a+b+2024,
∴ ab-a-b=2024,
∴ 原式=2024+1=2025.
故答案为:2025.
根据整式的乘法变形后,再将ab-a-b=2024代入,即可求得.
5.
解:
∴ m=-3,n=2,
∴ nm=2-3=.
故答案为: .
根据多项式乘多项式的法则计算后,各项的系数相同,求得m和n的值,再计算nm即可.
6.
解:四边形是长方形,
,
由折叠的性质得:,
,
,
,
,
,
,
,
故答案为:.
先根据矩形的性质可得,再根据折叠的性质可得,,然后根据邻补角的定义可得,最后根据三角形的内角和定理可得,由此即可得出答案.
7.-2
解:联立方程组得:,解得,
把代入4ax+5by=-28,ax-by=8中
得:,解得,
∴a-b==-2.
故答案为:-2.
联立不含a、b的方程为方程组并解之,求出xy的值,再建立关于a、b的方程组,解之即得a、b的值,再代入计算即可.
8.∠ABD=∠BDE(或∠ABE=∠DEC或∠ABE+∠BED=180°)
9.4x2 -6
解:原式=4x3÷x-6x÷x=4x2 -6.
故答案为:4x2 -6.
利用多项式除以单项式法则进行计算即可.
10.43;75
解:如图,过点B作,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴;
如图,延长,交于点H,
由上述可知,,
∵,,
∴,
∵,
∴,
∴,
∴.
故答案为:43,75.
在图2中,过点B作,易得,由平行线的性质:两直线平行,同旁内角互补可得,进而可得,以此求得,由平行线的性质即可得到;在图3中,延长,交于点H,由上述可求出,由三角形外角性质可得,再利用平行线的性质得到,则.
11.
12.﹣2x+7
解:方程2x+y=7,
解得:y=﹣2x+7.
故答案为:-2x+7.
将不含y的项移至右边即可.
13.1
解:根据题意得, ,
由 得, ,
把 代入 得, ,
解得 .
故答案为:1.
根据偶次幂及绝对值的非负性,由两个非负数的和为0,则每一个数都等于0,可得,解之即可.
14.8
解:∵ 2x+3y-3=0,
∴2x+3y=3
∴ 4x·8y=22x·23y=22x+3y=23=8.
故答案为:8.
根据等式得2x+3y=3,再利用积的乘方和幂的乘方的逆运算进行计算即可
15.(1)55
(2)45
解: (1)根据上下边互相平行可知,∠a=∠OAD,
∵a=70°,
∴∠OAD=70°.
又∵∠OAD+ 2β=180°,
∴β= 55°.
故答案为:55.
( 2 )根据折叠的性质可知,折叠两次后形成的三个角都相等,
根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为1 80°,故每个角为45°,
∴∠ACB=90°,即a=90°,
由(1)中可得,β=.
故答案为:45.
( 1 )根据两直线平行,同位角相等,可知∠OAD=α=70°,再利用折叠的性质可知∠OAD+ 2β=180°,如此即可求出β的值;
( 2 )根据折叠的性质可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,从而可知∠ACB=90°,再由(1)的思路可得β的值.
16.3
解:根据题意得,分母x-3为0时,分式无意义,
∴ x=3时,分式 无意义.
故答案为:3.
根据分式无意义的条件,即可求得.
17.(1)16
(2)130
解:(1)∵ S2=4,S2为正方形,
∴ S2的边长为2,
∵ FG=6,
∴ S3的边长为4,
∴ S3的面积为16;
(2)设长方形的长AD=a,宽AB=b,
则S3的面积为(a-8)(a-6),S1面积为2(b-8),S2的面积为(12-b)(14-a),
即2(a-8)(a-6)+2(b-8)-(12-b)(14-a)=42,
化简可得,ab=130.
故答案为:(1)16;(2)130.
(1)根据正方形的面积公式可得S2的边长,根据S3的边长求得其面积;
(2)设长方形的长AD=a,宽AB=b,分别用a和b表示出三个阴影面积,代入关系式计算即可求得ab的值,即为所求.
18.
解:
故答案为:.
根据同底数幂的除法法则计算即可.
19.80
解:如图所示,
∵ a∥b
∴∠1=∠3=100°
∵ ∠2+∠3=180°
∴ ∠2=80°
故答案为:80.
本题考查平行线的性质及邻补角,熟悉平行线的性质是解题关键。由 a∥b得∠1=∠3=100°
根据 ∠2+∠3=180°得 ∠2=80°.
20.65;53
解:如图:分别作出两个定日镜的法线:
∵反射光线与水平线的夹角是,镜面与立杆的夹角
∴
∵
∴
∴
∵光线是平行的
∴
∵反射光线与水平线的夹角是时
∴
∵
∴
则
∵
∴
故答案为:65,53
根据题意的新定义内容,作出法线,依据垂直的定义,结合已知角,得出,再利用角的运算,得出,结合光线是平行的,得出,结合已知角以及角的和差关系列式代入数值,进行计算,即可作答.
21.3x+5y
解:9x2+30xy+25y2=(3x+5y)2,
所以该正方形的边长为(3x+5y).
故答案为:(3x+5y).
将已知正方形的面积利用完全平方公式分解因式后,即可得出正方形的边长.
22.
解:∵
∴
∵关于x、y的二元一次方程组的解为
∴
解得
故答案为:
先整理得,结合换元思想即可得出,即可求解.
23.
解:
设,
原式=a(b+)-b(a-)=ab+-ab+=,
∵ a+b=1,
∴ 原式=.
故答案为:.
设,将原式化简后,再计算a+b,即可求得.
24.
解:∵ x-2y=0,
∴x=2y
∴
故答案为:.
由x-2y=0得x=2y,再代入分式求解即可.
25.5-3x
解:,
移项得:y=5-3x.
把含x项移到方程右边即可.
26.58或122
解:∵ ∠MFD=∠BEF=64°,
∴CD∥AB,
∴∠FGE=∠GEB,
∵平分∠BEF,
∴∠FEG=∠GEB=∠BEF=32°,
∴∠FGE=∠FEG=32°,
当GP在EG的上方时, 且,
∴∠PGF=∠PGE-∠FGE=90°-32°=58°,
当GP在EG的下方时, 且,
∠PGF=∠PGE+∠FGE=90°+32°=122°,
综上可知: ∠PGF的度数为58或122度.
故答案为:58或122.
先推出CD∥AB,利用平行线的性质及角平分线的定义可得∠FGE=∠FEG=32°,由,可分两种情况:当GP在EG的上方时和GP在EG的下方时,利用角的和差关系分别求解即可.
27.
解:∵的解是,
∴ 的解是
∴ .
故答案为: .
根据二元一次方程组 与 同解可得再解二元一次方程组即可求得.
28.60
解:,
,
,
故答案为:60.
根据平行线的判定及性质,即可解答.
29.
解:;
故答案为:.
观察此多项式的特点:含有公因式3a,因此先提取公因式,再利用公式法分解因式.
30.
解:
故答案为:
根据平方差公式计算即可.
31.
∵,
∴,.
∵,
∴,
同理,,
∴.
故答案为:.
先根据平角的定义分别求出,再根据平行线的性质求出,同理可得,而∠EPF=∠BPN+∠DPN,即可求得.
32.30
解:∵,,
∴,
∵平移得到,
∴,
∴,
故答案为:.
由三角形内角和定理可得,由平移可得,再根据平行线的性质即可求解.
33.2
解:设小长方形的宽为xcm,长为ycm,根据题意得:
解得:,
则小长方形的宽为2cm.
故答案为:2.
根据题意,设小长方形的宽为xcm,长为ycm,根据图形中的数量关系列出方程,求出方程的解,即可得出答案.
34.x(x﹣1)
=x(x﹣1).
故答案为:x(x﹣1).
观察此多项式的特点:含有公因式x,由此利用提公因式法分解因式。
35.62°或62度
解:如图,
∵ 直尺的上下边平行,
∴ ∠2=∠3,
∵ ∠ABC=90°,
∴ ∠1+∠3=90°,
∴ ∠1+∠2=90°,
∵ ∠1=28°,
∴ ∠2=62°.
故答案为:62°或62度.
根据平行线的性质可得∠2=∠3,再利用∠1与∠3互余,即可求得.
36.14
解:=2x2+(m-14)x-7m,
∵ 原式展开后的结果中不含的一次项,
∴m-14=0,
解得m=14.
故答案为:14.
利用多项式乘多项式将原式展开,由原式展开后的结果中不含的一次项, 可得m-14=0,解之即可.
37.3
解:由数轴可知,点A表示的数为-3,则点B表示的数为,且>0
∵ 点A,B到原点的距离相等,
∴=
∴ a=3a-6
解得:a=3
故答案为:3.
本题考查绝对值,熟练掌握绝对值的知识是解题关键。由数轴可知,点A表示的数为-3,则点B表示的数为,根据点A,B到原点的距离相等可得=,求解可得a.
38.(1)0
(2)4
解:(1)由图形摆放可知,正方形甲的边长为a, =a2,正方形乙的边长为a-b, 图①中的阴影部分面积为 =2a(a-b), 图②中的阴影部分面积为 =a2-(a-b)2,
∵
∴ 2a(a-b)+a2-(a-b)2=a2
整理得:a2-2b2=0
∴
故答案为:0.
(2)∵
∴ 2a(a-b)=a2-(a-b)2,
整理得:2a2+b2=4ab
∴
本题考查整式的应用及分式的化简,应用整体代入的思想求值是解题关键。根据图形,列出 =a2, =2a(a-b), =a2-(a-b)2,(1)根据,化简得a2-2b2=0,得;(2)由得2a2+b2=4ab,则.
39.12.5
解:由平移知:AD=BE=2.5,AD∥BE,
∴四边形ABED是平行四边形,
∴ 四边形的面积为BE·AC=2.5×5=12.5.
故答案为:12.5.
利用平移的性质可推出四边形ABED是平行四边形,BE=2.5,根据平行四边形的面积公式进行计算即可.
40.54°
解:
∵AE平分∠DAF,
∴设∠EAF=∠DAE=x,
又∵AD⊥PQ,,,
∴∠AFD=90°-∠DAF=90°-2x,∠ACB=,∠ACD=90°-∠CAE-∠DAE=45°-x,
∴∠BCQ=∠ACB+∠ACD=+(45°-x)=,
又∵AB∥PQ,
∴∠MBC=∠BCQ=,
又∵BC平分∠ABM,
∴∠ABM=2∠MBC=3x+90°,
∴∠ABN=180°-∠ABM=90°-3x,
如图,过点A作AG∥MN,
∵MN∥PQ,
∴AG∥PQ,
∴∠BAG=∠ABN=90°-3x,∠FAG=∠AFD=90°-2x,
又∵AB⊥AF,
∴∠BAF=∠ABN+∠AFD=(90°-3x)+(90°-2x)=90°,解得x=18°,
∴∠AFD=90°-2x=90°-36°=54°,
故填:54°.
由已知条件的角度关系,根据角度较小且含多个角度直接关联,可直接设∠EAF=∠DAE=x,利用已知条件信息及平行线的性质逐一表示各个角度,为求出目标角的度数,在表示的基础上进一步利用“猪蹄模型”得出等量关系解之即可.
41.m(m+1)(m﹣1)
解:原式=m(m2﹣12)
=m(m+1)(m﹣1).
故答案为:m(m+1)(m﹣1).
利用提公因式法与公式法计算即可。
42.1
根据乘法公式多项式乘以多项式,用第一个多项式的每一项乘以第二个多项式的每一项,可求 (m-1)(n-1) = mn-m-n+1=mn-(m+n)+1,直接代入m+n=mn可求得 (m-1)(n-1) = 1.
利用多项式乘以多项式的法则可算出答案。
43.30
解:∵,,
∴;
故答案为:30.
直接用同底数幂相乘计算即可.
44.(1)5
(2)
45.2
解:把代入
得:
解得:.
故答案为:2
将方程的解代入方程即可求出参数k的值.
46.45°
解:如图,点D在线段AB上时,DE∥BC
∴ ∠EDC=∠BCD
由折叠知:∠EDC=∠CDB,∠ECD=∠BCD
∴ ∠EDC=∠BCD=∠CDB=∠ECD
∵ ∠ABC=90°
∴ ∠CDB=∠EDC=∠BCD=∠ECD=45°,此时EC∥BD
∴ ∠CDB=45°
故答案为:45°.
本题考查折叠的性质,平行线的性质,掌握折叠的性质和平行线的性质是解题关键。由DE∥BC得∠EDC=∠BCD,根据折叠得∠EDC=∠CDB,∠ECD=∠BCD,可得 ∠CDB=45°.
同课章节目录
