2024-2025学年浙教版七年级数学下册期中真题专项复习09填空题(含答案)(浙江专用)
文档属性
| 名称 | 2024-2025学年浙教版七年级数学下册期中真题专项复习09填空题(含答案)(浙江专用) |  | |
| 格式 | docx | ||
| 文件大小 | 428.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 21:40:20 | ||
图片预览


文档简介
2024-2025学年七年级数学下册期中真题专项复习09填空题
1.(2024七下·奉化期中)新冠病毒的直径大约是0.000014厘米长,0.000014用科学记数法表示为 .
2.(2024七下·温州期中)如图,将长为 ,宽为 的长方形 先向右平移 ,再向下平移 ,得到长方形 ,则阴影部分的面积为 .
3.(2024七下·吴兴期中) 如图,,平分,,则 度.
4.(2024七下·宁海期中)已知4x﹣2y=3,用含x的代数式表示y,则y= .
5.(2024七下·温州期中) 如图,点E、H分别在直线AB、CD上,若,且在平行线内部有两点F、G,满足,,,则 °.
6.(2024九上·崆峒期中)因式分解 = .
7.(2024七下·温州期中) 大长方形中按如图所示的方式摆放五个完全相同的小长方形,若一个小长方形的面积为,阴影部分的面积为20,则大长方形的周长为 .
8.(2024七下·吴兴期中)已知方程,用含x的代数式表示y,那么y= .
9.(2024七下·香坊期末)已知二元一次方程,用关于的代数式表示,则 .
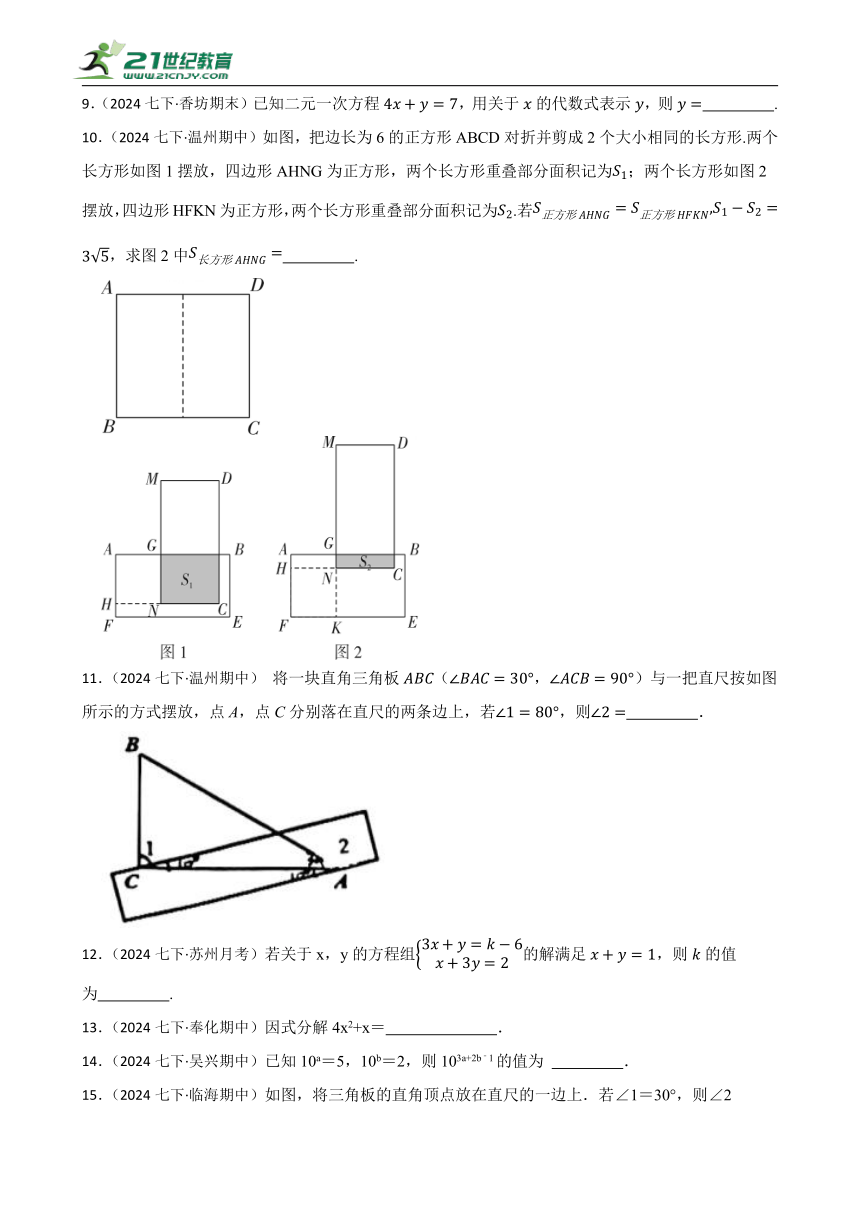
10.(2024七下·温州期中)如图,把边长为6的正方形ABCD对折并剪成2个大小相同的长方形.两个长方形如图1摆放,四边形AHNG为正方形,两个长方形重叠部分面积记为;两个长方形如图2摆放,四边形HFKN为正方形,两个长方形重叠部分面积记为.若,求图2中 .
11.(2024七下·温州期中) 将一块直角三角板(,)与一把直尺按如图所示的方式摆放,点A,点C分别落在直尺的两条边上,若,则 .
12.(2024七下·苏州月考)若关于x,y的方程组的解满足,则的值为 .
13.(2024七下·奉化期中)因式分解4x2+x= .
14.(2024七下·吴兴期中)已知10a=5,10b=2,则103a+2b﹣1的值为 .
15.(2024七下·临海期中)如图,将三角板的直角顶点放在直尺的一边上.若∠1=30°,则∠2= °.
16.(2024七下·奉化期中)如图,将一条两边沿互相平行的纸带折叠,若∠1=44°,则∠α= .
17.(2024七下·温州期中) 计算: .
18.(2024七下·奉化期中)已知,,则 .
19.(2024七下·温州期中)若,则 .
20.(2024七下·温州期中) 如图,要使,只需添加一个条件,这个条件是 .
21.(2024七下·温州期中) 已知,用含x的代数式表示y,则 .
22.(2024七下·温州期中) 若关于x,y的二元一次方程组的解是,则关于a,b的二元一次方程组的解是 .
23.(2024七下·义乌期中)已知关于x,y的二元一次方程组 的解为 ,则关于m,n的二元一次方程组 的解为 .
24.(2024七下·宁海期中)已知a,b是常数,若化简(﹣x+a)(2x2+bx﹣3)的结果不含x的二次项,则2b﹣4a= .
25.(2024七下·宁海期中)若2x+y﹣3=0,则52x 5y= .
26.(2024七下·临海期中)已知二元一次方程组则x-y的值为 .
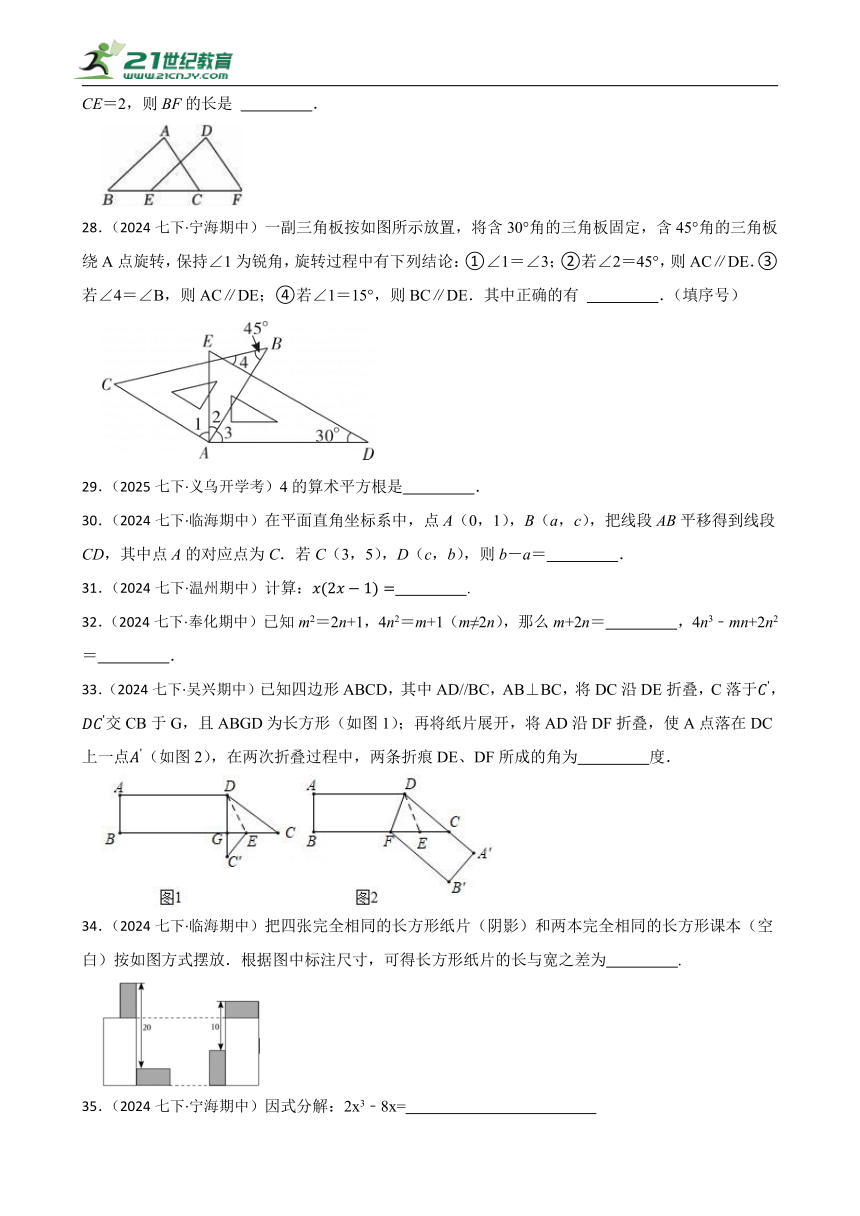
27.(2024七下·宁海期中)如图,若△DEF是由△ABC经过平移后得到,已知A,D之间的距离为1,CE=2,则BF的长是 .
28.(2024七下·宁海期中)一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 .(填序号)
29.(2025七下·义乌开学考)4的算术平方根是 .
30.(2024七下·临海期中)在平面直角坐标系中,点A(0,1),B(a,c),把线段AB平移得到线段CD,其中点A的对应点为C.若C(3,5),D(c,b),则b-a= .
31.(2024七下·温州期中)计算: .
32.(2024七下·奉化期中)已知m2=2n+1,4n2=m+1(m≠2n),那么m+2n= ,4n3﹣mn+2n2= .
33.(2024七下·吴兴期中)已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于,交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为 度.
34.(2024七下·临海期中)把四张完全相同的长方形纸片(阴影)和两本完全相同的长方形课本(空白)按如图方式摆放.根据图中标注尺寸,可得长方形纸片的长与宽之差为 .
35.(2024七下·宁海期中)因式分解:2x3﹣8x=
36.(2024七下·温州期中)已知,则的值为 .
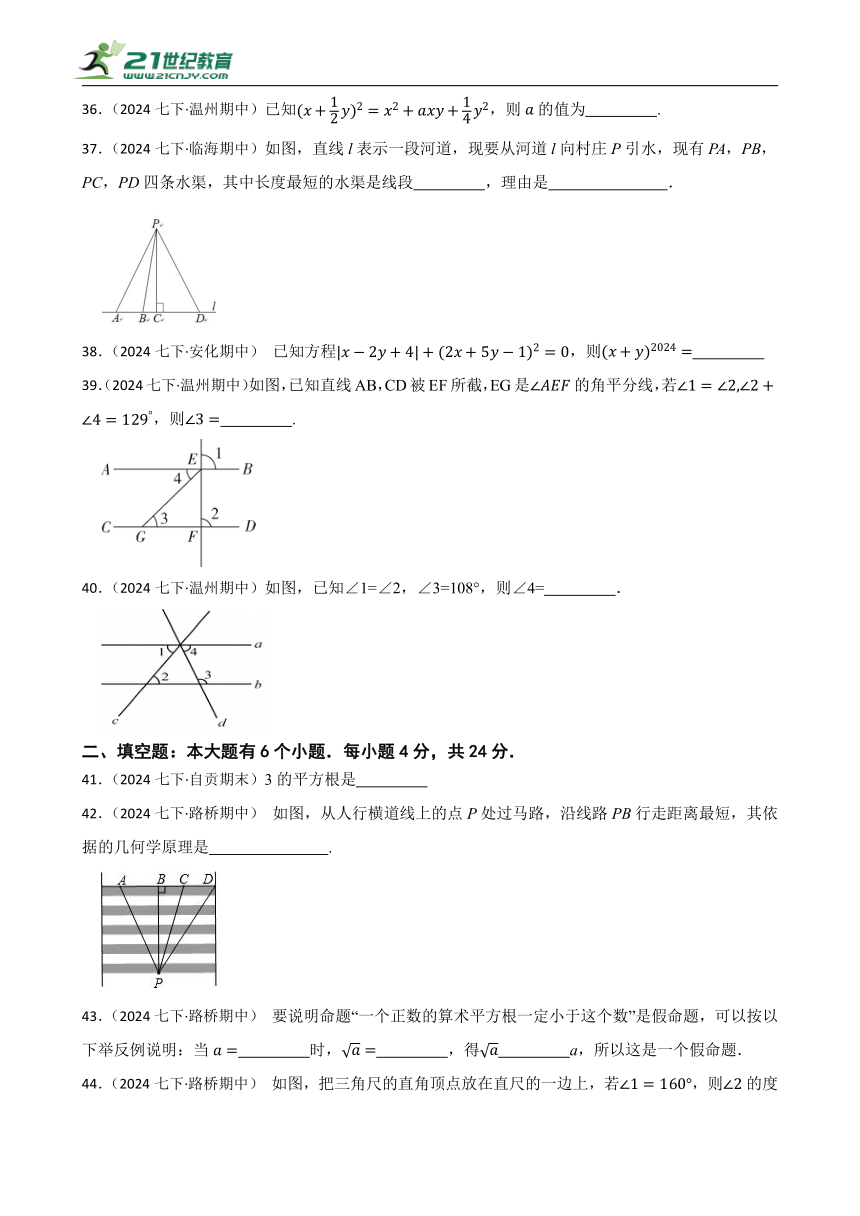
37.(2024七下·临海期中)如图,直线l表示一段河道,现要从河道l向村庄P引水,现有PA,PB,PC,PD四条水渠,其中长度最短的水渠是线段 ,理由是 .
38.(2024七下·安化期中) 已知方程,则
39.(2024七下·温州期中)如图,已知直线AB,CD被EF所截,EG是的角平分线,若,则 .
40.(2024七下·温州期中)如图,已知∠1=∠2,∠3=108°,则∠4= .
二、填空题:本大题有6个小题.每小题4分,共24分.
41.(2024七下·自贡期末)3的平方根是
42.(2024七下·路桥期中) 如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是 .
43.(2024七下·路桥期中) 要说明命题“一个正数的算术平方根一定小于这个数”是假命题,可以按以下举反例说明:当 时, ,得 a,所以这是一个假命题.
44.(2024七下·路桥期中) 如图,把三角尺的直角顶点放在直尺的一边上,若,则的度数为 .
45.(2024七下·路桥期中) 我国民间流传着许多趣味算题,它们多以顺口溜的形式表达,其中《孙子算经》中记我了这样一个数学问题:一群老人去赶集,半路买了一堆梨,一人一个多一梨,一人两个少二梨,请问君子知道否,几个老人几个梨?若设有x个老人,y个梨,则可列出的方程组为 .
46.(2024七下·路桥期中) 在平面直角坐标系中,线段CD是由线段AB平移所得,已知,则下列4个结论中,正确的有 .(填序号)
①;②;③四边形ABCD的面积为10;④点D坐标为.
答案解析部分
1.1.4×10﹣5
解: 0.000014 =1.4×10-5.
故答案为:1.4×10-5.
用科学记数法表示绝对值非常小的数,一般表示成a×10-n的形式,其中1≤∣a∣<10,n等原数左边第一个非0数字前面所有0的个数,包括小数点前面的那个0,根据方法即可得出答案.
2.18
解:根据平移的性质得出中间小长方形的长为3cm,宽为2cm,
∴ 阴影部分的面积=2×5×3-2×3×2=18cm2.
根据平移的性质得出中间小长方形的长和宽,再利用阴影部分的面积=两个大长方形的面积和-两个小长方形的面积,代入数值进行计算,即可得出答案.
3.70
解:∵,
∴,,
∵平分,
∴,
故答案为:.
根据平行线的性质可得,,再由角平分线的定义求出∠DCE即可.
4.
解:移项得,,
把y的系数化为1得,,
故答案为:.
移项后把y的系数化为1即可.
5.70
解:延长HG交AB于点P,如图所示:
∵∠AEF=120°,
∴∠BEF=60°.
∵∠FGH=80°,
∴∠FGP=100°.
又∵EF⊥FG,
∴∠EFG=90°.
∴∠EPH=360°-∠BEF-∠EFG-∠FGP=110°.
∵,
∴ 180°-∠EPH=70°.
故答案为:70.
延长HG交AB于点P,利用多边形内角和公式求出∠EPH的度数,再利用平行线的性质定理即可求解.
6.
解:原式 ,
故答案为: .
观察此多项式的特点:两项都含有公因式a,由此利用提取公因式法分解因式.
7.6
解:设小长方形的宽为,长为,如图,
∴大的长方形的长为,宽为,
∵阴影部分的面积为20,
∴,
∴,
即
∴,
∴,
∵,
∴,
∵,
∴,而,
∴,
∴,
∴,
∴大长方形的周长为;
故答案为:
设小长方形的宽为,长为,可表示出小长方形的面积,大长方形的长与宽,以及阴影部分的面积,从而可得关于x和y的方程,即,,整理得和,根据x>y>0,可开方得到x+y与x-y的值,从而可求得y值,代入即可得到大长方形的周长.
8.
9.y=7-4x
解:,
移项得:y=7-4x.
故答案为:y=7-4x.
直接将4x移到方程的右边即可.
10.1
解:由折叠知:CN=GK=3,
∵,
∴图1中GN=图2中NK,
设正方形边长为x
∵S1=GN·CN=3x,S2=CN(GK-KN)=3(3-x),
∴S1-S2=3x-3(3-x)=,
∴x=,
∴图2中GN=3-=,HN=x=,
∴ 图2中·=1.
故答案为:1.
由,可设两正方形边长为x,可得S1=GN·CN=3x,S2=CN(GK-KN)=3(3-x),由S1-S2=可求x知,从而求出图2中GN、HN的长,再根据长方形面积计算方法进行计算即可.
11.
解:由题意得:, ,
∵∠1=80°,
∴∠α=10°,
∴∠2=180°-∠α-∠BAC=180°-10°-30°=140°.
故答案为:140°.
利用角的和差运算求得∠α的值,再根据平行线的性质和平角的定义即求得∠2的度数.
12.8
解:,
①+②得4x+4y=k-4,
∴x+y=,
∵,
∴=1,解得k=8.
故答案为:8.
将方程组中两方程相加,可得x+y=,即得=1,解之即可.
13.x(4x+1)
解:4x2+x=x(4x+1).
故答案为:x(4x+1).
直接提取公因式x即可.
14.50
解:∵10a=5,10b=2,
∴103a+2b-1=103a×102b÷10=(10a)3×(10b)2÷10=53×22÷10=50.
故答案为:50.
“同底数幂乘法、同底数幂除法、幂的乘方”三种幂运算法则的逆运用,将103a+2b-1整理成(10a)3×(10b)2÷10,最后代入数值进行计算即可求解.
15.60
解: 如图:
∵∠EFG=90°,∠1=30°,
∴∠3=∠EFG-∠1=60°,
∵AB∥CD,
∴∠2=∠3=60°,
故答案为:60.
先求出∠3=60°,根据两直线平行,同位角相等可得∠2=∠3=60°.
16.68°
解:∵纸片两边平行,
∴∠2=∠1=44°,
由折叠的性质得:2∠α+∠2=180°,
∴∠α=68°.
故答案为:68°.
由平行线的性质可得∠2=∠1=44°,利用折叠的性质得2∠α+∠2=180°,据此计算即可.
17.
解:.
故答案为:
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式.
18.200
∵,,
∴,
故答案为:200.
将,代入计算即可.
19.12
解: ∵,
∴=6×2=12.
故答案为:12.
利用同底数幂的乘法法则的逆用将待求式子化为,再代入计算即可.
20.(答案不唯一)
解:当,
可得,
故答案为:(答案不唯一)
根据平行线的判定定理判断即可.
21.
解:,
故答案为:
移项后等式两边同×(-1),即可得到y关于x的代数式.
22.
解:∵关于x,y的二元一次方程组的解是,令a+b=x,2a-b=y
∴ 则关于a,b的二元一次方程组可变形成,
故解为,即
①+②得:3a=6,解得a=2,
代入①得:2+b=1,解得:b=-1.
故方程组的解为:
故答案为:.
观察发现两个方程为同解方程,故可根据第一个方程的解得到第二个方程的解,再求解即可.
23.
解:由题意可得,
解得,
∴关于m、n的二元一次方程组的解为.
由题意可得,求出m、n的值,据此可得方程组的解.
24.0
解:
,
∵结果不含x的二次项,
∴,
∴.
故答案为:0.
先根据多项式乘以多项式的运算法则展开,再根据结果不含x的二次项可得x的二次项系数为0,然后对所求式子变形,整体代入计算即可.
25.125
解:∵,
∴,
∴.
故答案为:125.
先求出,再根据同底数幂的乘法的法则进行计算即可.
26.1
解:,
由①得③,
把③代入②得:,
解得:,
,
∴
故答案为:1.
利用代入消元法,解二元一次方程组,进而得出的值.
27.4
解:∵是由沿向右移动得到的,
∴,
∴.
故答案为:4.
根据平移的性质可得到,然后计算即可.
28.①③④
解:设AB与DE的交点为F
∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,故①正确;
∵∠2=45°,∠E=60°,
∴∠EFB=∠E+∠2=105°,
∴∠EFB≠∠CAB,
∴AC与DE不平行,故②错误;
∵∠4=∠B=45°,∠C=45°,
∴∠4=∠C,
∴AC∥DE,故③正确;
当∠1=15°时, ∠2=90°-15°=75°,
∴∠EFB=∠E+∠2=60°+75°=135°.
∵∠B=45°,
∴∠B+∠EFB=180°,
∴BC∥DE,故④正确.
综上可得:①③④正确.
故答案为:①③④.
设AB与DE的交点为F,根据同角的余角相等可判断①;由外角的性质可得∠EFB=∠E+∠2=105°,根据平行线的判定定理可判断②;根据∠4=∠B=45°,∠C=45°可得∠4=∠C,根据平行线的判定定理可判断③;由余角的性质可得 ∠2=90°-∠1=75°,根据外角的性质可得∠EFB=∠E+∠2=60°+75°=135°,则∠B+∠EFB=180°,据此判断④.
29.2
解:∵22=4,
∴4的算术平方根是2.
故答案为:2.
依据算术平方根的定义求解即可.
30.7
解:∵把线段AB平移得到线段CD,其中点A的对应点为C,且点A(0,1),C(3,5)
∴0+3=3,1+4=5,
∴把线段AB向上平移4个单位,向右平移3个单位得到线段CD,
∵点B与点D是对应点,且 B(a、c),D(c,d),
∴a+3=c,c+4=b,
∴a=c-3,b=c+4,
∴b-a=c+4-(c-3)=4+3=7.
故答案为:7.
根据横坐标,右移加,左移减;纵坐标,上移加,下移减先求出平移的方向和单位,即可求解.
31.
解:2x2-x.
故答案为:2x2-x.
利用单项式乘多项式法则“单项式乘以多项式,就是用单项式去乘以多项式的每一项,再把所得的积相加”将原式展开即可.
32.-1;0
解:∵m2=2n+1①,4n2=m+1②(m≠2n) ,
①-②得:m2-4n2=2n-m,
∴(m+2n)(m-2n)=2n-m,
∵m≠2n,
∴2n-m≠0,
∴m+2n=-1.
∵ 4n2=m+1 ,
∴ 4n3=mn+n ,2n2=(m+1),
∴ 4n3﹣mn+2n2=mn+n -mn+(m+1)=n+m+=(m+2n) +=×(-1)+=0
故答案为:-1,0.
(1)将两等式相减可得m2-4n2=2n-m,再利用平方差公式变形,从而求解;
(2) 由4n2=m+1 可求4n3=mn+n ,2n2=(m+1),然后代入待求式子整理化简,再整体代入计算即可.
33.45
解:如图,过点D作DG⊥BC于点G,
设∠CDE=α,∠FDG=β,
∴根据折叠性质得∠GDE=∠CDE=α,∠ADF=∠FDC,
∴∠FDC=∠ADF=∠FDG+∠GDE+∠CDE=β+α+α=β+2α,
∵四边形ABGD是矩形,
∴∠ADG=90°,
∴∠AGD=∠ADF+∠FDG=β+2α+β=90°,
∴β+α=45°,
∴折痕DE、DF所成的角为∠FDE=β+α=45°.
故答案为:45.
过点D作DG⊥BC于点G,设∠CDE=α,∠FDG=β,根据折叠的性质得∠GDE=∠CDE=α,∠ADF=∠FDC,从而求出∠ADF=β+2α,再根据矩形的性质求出β+α=45°后即可得到答案.
34.5
解:设小长方形的长为x,宽为y,
根据题意得:20+y-x=10+x-y,
即2x-2y=20-10,
整理得:,
小长方形的长与宽的差是5,
故答案为:5.
设小长方形的长为x,宽为y,根据两种不同的摆放方式分别表示出长方形课本的长,进而根据长方形课本的长不变列出方程,求出x-y的值即可.
35. 2x(x+2)(x﹣2)
解:2x3﹣8x=2x(x2﹣4)=2x(x+2)(x﹣2).
故答案为:2x(x+2)(x﹣2).
先提公因式2x,分解成2x(x2﹣4),而x2﹣4可利用平方差公式分解.
36.1
解: ∵,
∴xy=axy,
∴a=1.
故答案为:1.
利用完全平方公式将等式左边展开,利用等式对应项系数相等即可求解.
37.PC;垂线段最短
解:如图,直线l表示一段河道,现要从河道l向村庄P引水,现有PA,PB,PC,PD四条水渠,其中长度最短的水渠是线段PC,理由是垂线段最短.
故答案为:PC,垂线段最短.
根据从直线外一点,到直线上任意一点所引的线段中,垂直线段最短进行求解即可.
38.1
解:∵
∴
解得:,
∴,
故答案为:.
根据绝对值和偶次方的非负性得出关于x,y的二元一次方程组,解方程组求出x,y,然后计算即可.
39.43°
解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠4,∠AEF=∠2,
∵ EG是的角平分线,
∴∠2=∠AEF=2∠4,
∵∠2+∠4=129°,
∴3∠4=129°,
∴∠4=43°,
∴∠3=43°.
故答案为:43°.
由同位角相等,两直线平行,可得AB∥CD,利用两直线平行,内错角相等可得∠3=∠4,∠AEF=∠2,再由角平分线的定义可得∠2=∠AEF=2∠4,结合∠2+∠4=129°可求出∠4的度数,继而得解.
40.72°
解:∵ ∠1=∠2 ,
∴a∥b(内错角相等,两直线平行),
∴∠3+∠4=180°(二直线平行,同旁内角互补),
∵∠3=108°,
∴∠4=180°-108°=72°.
故答案为:72°.
由内错角相等,两直线平行得a∥b,由二直线平行,同旁内角互补得∠3+∠4=180°,再代入∠3的度数即可求出∠4的度数.
41.
解:∵( )2=3,
∴3的平方根是为 .
故答案为:± .
直接根据平方根的概念即可求解.
42.垂线段最短
解:∵PB⊥AD,垂足点为B,
∴沿线路PB行走距离最短,其依据的几何学原理是垂线段最短.
故答案为:垂线段最短.
根据垂线段最短的性质,即可得到答案.
43.;;
解:当时,,
∵,
∴,
∴这是一个假命题.
故答案为:、、.
举例说明一个命题是假命题的反例,需要满足命题的题设,不满足命题的结论,据此解答即可.
44.
解:如图,
∵∠1=160°,∠C=90°,
∴∠3=∠1-∠C=70°,
∴∠2=∠3=70°.
故答案为:70°.
根据三角形的外角性质得到∠3=∠1-∠C=70°,再根据对顶角相等得到∠2=∠3,即可得到答案.
45.
解:设有x个老人,y个梨,
根据题意可列方程:.
故答案为:.
设有x个老人,y个梨,根据“ 一人一个多一梨”可列方程x+1=y,根据“ 一人两个少二梨 ”可列方程2x-2=y,联立两方程,即可得到答案.
46.①②③
解:①∵ 线段CD是由线段AB平移所得,
∴AD//BC,故①正确;
②∵AD//BC,AB//CD,
∴∠ADC+∠DAB=180°,∠DAB+∠ABC=180°,
∴∠ADC=∠ABC,故②正确;
③∵,
∴,
∴,故③正确;
④ 根据题意可知,线段CD是由线段AB向右平移2个单位,再向上平移2个单位得到,
∵A(-3,0),
∴D(-1,2),故④错误;
综上所述,①②③正确.
故答案为:①②③.
根据平移的性质可得AD//BC,AB//CD,据此可判断①;再根据二直线平行,同旁内角互补可得∠ADC+∠DAB=180°,∠DAB+∠ABC=180°,由同角的补角相等得∠ADC=∠ABC,据此可判断②;根据点的坐标与图形的性质、三角形面积公式及平移的性质可对③进行判断;根据点的坐标平移规律“横坐标左移减右移加,纵坐标上移加下移减”可对④进行判断.
1.(2024七下·奉化期中)新冠病毒的直径大约是0.000014厘米长,0.000014用科学记数法表示为 .
2.(2024七下·温州期中)如图,将长为 ,宽为 的长方形 先向右平移 ,再向下平移 ,得到长方形 ,则阴影部分的面积为 .
3.(2024七下·吴兴期中) 如图,,平分,,则 度.
4.(2024七下·宁海期中)已知4x﹣2y=3,用含x的代数式表示y,则y= .
5.(2024七下·温州期中) 如图,点E、H分别在直线AB、CD上,若,且在平行线内部有两点F、G,满足,,,则 °.
6.(2024九上·崆峒期中)因式分解 = .
7.(2024七下·温州期中) 大长方形中按如图所示的方式摆放五个完全相同的小长方形,若一个小长方形的面积为,阴影部分的面积为20,则大长方形的周长为 .
8.(2024七下·吴兴期中)已知方程,用含x的代数式表示y,那么y= .
9.(2024七下·香坊期末)已知二元一次方程,用关于的代数式表示,则 .
10.(2024七下·温州期中)如图,把边长为6的正方形ABCD对折并剪成2个大小相同的长方形.两个长方形如图1摆放,四边形AHNG为正方形,两个长方形重叠部分面积记为;两个长方形如图2摆放,四边形HFKN为正方形,两个长方形重叠部分面积记为.若,求图2中 .
11.(2024七下·温州期中) 将一块直角三角板(,)与一把直尺按如图所示的方式摆放,点A,点C分别落在直尺的两条边上,若,则 .
12.(2024七下·苏州月考)若关于x,y的方程组的解满足,则的值为 .
13.(2024七下·奉化期中)因式分解4x2+x= .
14.(2024七下·吴兴期中)已知10a=5,10b=2,则103a+2b﹣1的值为 .
15.(2024七下·临海期中)如图,将三角板的直角顶点放在直尺的一边上.若∠1=30°,则∠2= °.
16.(2024七下·奉化期中)如图,将一条两边沿互相平行的纸带折叠,若∠1=44°,则∠α= .
17.(2024七下·温州期中) 计算: .
18.(2024七下·奉化期中)已知,,则 .
19.(2024七下·温州期中)若,则 .
20.(2024七下·温州期中) 如图,要使,只需添加一个条件,这个条件是 .
21.(2024七下·温州期中) 已知,用含x的代数式表示y,则 .
22.(2024七下·温州期中) 若关于x,y的二元一次方程组的解是,则关于a,b的二元一次方程组的解是 .
23.(2024七下·义乌期中)已知关于x,y的二元一次方程组 的解为 ,则关于m,n的二元一次方程组 的解为 .
24.(2024七下·宁海期中)已知a,b是常数,若化简(﹣x+a)(2x2+bx﹣3)的结果不含x的二次项,则2b﹣4a= .
25.(2024七下·宁海期中)若2x+y﹣3=0,则52x 5y= .
26.(2024七下·临海期中)已知二元一次方程组则x-y的值为 .
27.(2024七下·宁海期中)如图,若△DEF是由△ABC经过平移后得到,已知A,D之间的距离为1,CE=2,则BF的长是 .
28.(2024七下·宁海期中)一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 .(填序号)
29.(2025七下·义乌开学考)4的算术平方根是 .
30.(2024七下·临海期中)在平面直角坐标系中,点A(0,1),B(a,c),把线段AB平移得到线段CD,其中点A的对应点为C.若C(3,5),D(c,b),则b-a= .
31.(2024七下·温州期中)计算: .
32.(2024七下·奉化期中)已知m2=2n+1,4n2=m+1(m≠2n),那么m+2n= ,4n3﹣mn+2n2= .
33.(2024七下·吴兴期中)已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于,交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为 度.
34.(2024七下·临海期中)把四张完全相同的长方形纸片(阴影)和两本完全相同的长方形课本(空白)按如图方式摆放.根据图中标注尺寸,可得长方形纸片的长与宽之差为 .
35.(2024七下·宁海期中)因式分解:2x3﹣8x=
36.(2024七下·温州期中)已知,则的值为 .
37.(2024七下·临海期中)如图,直线l表示一段河道,现要从河道l向村庄P引水,现有PA,PB,PC,PD四条水渠,其中长度最短的水渠是线段 ,理由是 .
38.(2024七下·安化期中) 已知方程,则
39.(2024七下·温州期中)如图,已知直线AB,CD被EF所截,EG是的角平分线,若,则 .
40.(2024七下·温州期中)如图,已知∠1=∠2,∠3=108°,则∠4= .
二、填空题:本大题有6个小题.每小题4分,共24分.
41.(2024七下·自贡期末)3的平方根是
42.(2024七下·路桥期中) 如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的几何学原理是 .
43.(2024七下·路桥期中) 要说明命题“一个正数的算术平方根一定小于这个数”是假命题,可以按以下举反例说明:当 时, ,得 a,所以这是一个假命题.
44.(2024七下·路桥期中) 如图,把三角尺的直角顶点放在直尺的一边上,若,则的度数为 .
45.(2024七下·路桥期中) 我国民间流传着许多趣味算题,它们多以顺口溜的形式表达,其中《孙子算经》中记我了这样一个数学问题:一群老人去赶集,半路买了一堆梨,一人一个多一梨,一人两个少二梨,请问君子知道否,几个老人几个梨?若设有x个老人,y个梨,则可列出的方程组为 .
46.(2024七下·路桥期中) 在平面直角坐标系中,线段CD是由线段AB平移所得,已知,则下列4个结论中,正确的有 .(填序号)
①;②;③四边形ABCD的面积为10;④点D坐标为.
答案解析部分
1.1.4×10﹣5
解: 0.000014 =1.4×10-5.
故答案为:1.4×10-5.
用科学记数法表示绝对值非常小的数,一般表示成a×10-n的形式,其中1≤∣a∣<10,n等原数左边第一个非0数字前面所有0的个数,包括小数点前面的那个0,根据方法即可得出答案.
2.18
解:根据平移的性质得出中间小长方形的长为3cm,宽为2cm,
∴ 阴影部分的面积=2×5×3-2×3×2=18cm2.
根据平移的性质得出中间小长方形的长和宽,再利用阴影部分的面积=两个大长方形的面积和-两个小长方形的面积,代入数值进行计算,即可得出答案.
3.70
解:∵,
∴,,
∵平分,
∴,
故答案为:.
根据平行线的性质可得,,再由角平分线的定义求出∠DCE即可.
4.
解:移项得,,
把y的系数化为1得,,
故答案为:.
移项后把y的系数化为1即可.
5.70
解:延长HG交AB于点P,如图所示:
∵∠AEF=120°,
∴∠BEF=60°.
∵∠FGH=80°,
∴∠FGP=100°.
又∵EF⊥FG,
∴∠EFG=90°.
∴∠EPH=360°-∠BEF-∠EFG-∠FGP=110°.
∵,
∴ 180°-∠EPH=70°.
故答案为:70.
延长HG交AB于点P,利用多边形内角和公式求出∠EPH的度数,再利用平行线的性质定理即可求解.
6.
解:原式 ,
故答案为: .
观察此多项式的特点:两项都含有公因式a,由此利用提取公因式法分解因式.
7.6
解:设小长方形的宽为,长为,如图,
∴大的长方形的长为,宽为,
∵阴影部分的面积为20,
∴,
∴,
即
∴,
∴,
∵,
∴,
∵,
∴,而,
∴,
∴,
∴,
∴大长方形的周长为;
故答案为:
设小长方形的宽为,长为,可表示出小长方形的面积,大长方形的长与宽,以及阴影部分的面积,从而可得关于x和y的方程,即,,整理得和,根据x>y>0,可开方得到x+y与x-y的值,从而可求得y值,代入即可得到大长方形的周长.
8.
9.y=7-4x
解:,
移项得:y=7-4x.
故答案为:y=7-4x.
直接将4x移到方程的右边即可.
10.1
解:由折叠知:CN=GK=3,
∵,
∴图1中GN=图2中NK,
设正方形边长为x
∵S1=GN·CN=3x,S2=CN(GK-KN)=3(3-x),
∴S1-S2=3x-3(3-x)=,
∴x=,
∴图2中GN=3-=,HN=x=,
∴ 图2中·=1.
故答案为:1.
由,可设两正方形边长为x,可得S1=GN·CN=3x,S2=CN(GK-KN)=3(3-x),由S1-S2=可求x知,从而求出图2中GN、HN的长,再根据长方形面积计算方法进行计算即可.
11.
解:由题意得:, ,
∵∠1=80°,
∴∠α=10°,
∴∠2=180°-∠α-∠BAC=180°-10°-30°=140°.
故答案为:140°.
利用角的和差运算求得∠α的值,再根据平行线的性质和平角的定义即求得∠2的度数.
12.8
解:,
①+②得4x+4y=k-4,
∴x+y=,
∵,
∴=1,解得k=8.
故答案为:8.
将方程组中两方程相加,可得x+y=,即得=1,解之即可.
13.x(4x+1)
解:4x2+x=x(4x+1).
故答案为:x(4x+1).
直接提取公因式x即可.
14.50
解:∵10a=5,10b=2,
∴103a+2b-1=103a×102b÷10=(10a)3×(10b)2÷10=53×22÷10=50.
故答案为:50.
“同底数幂乘法、同底数幂除法、幂的乘方”三种幂运算法则的逆运用,将103a+2b-1整理成(10a)3×(10b)2÷10,最后代入数值进行计算即可求解.
15.60
解: 如图:
∵∠EFG=90°,∠1=30°,
∴∠3=∠EFG-∠1=60°,
∵AB∥CD,
∴∠2=∠3=60°,
故答案为:60.
先求出∠3=60°,根据两直线平行,同位角相等可得∠2=∠3=60°.
16.68°
解:∵纸片两边平行,
∴∠2=∠1=44°,
由折叠的性质得:2∠α+∠2=180°,
∴∠α=68°.
故答案为:68°.
由平行线的性质可得∠2=∠1=44°,利用折叠的性质得2∠α+∠2=180°,据此计算即可.
17.
解:.
故答案为:
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式.
18.200
∵,,
∴,
故答案为:200.
将,代入计算即可.
19.12
解: ∵,
∴=6×2=12.
故答案为:12.
利用同底数幂的乘法法则的逆用将待求式子化为,再代入计算即可.
20.(答案不唯一)
解:当,
可得,
故答案为:(答案不唯一)
根据平行线的判定定理判断即可.
21.
解:,
故答案为:
移项后等式两边同×(-1),即可得到y关于x的代数式.
22.
解:∵关于x,y的二元一次方程组的解是,令a+b=x,2a-b=y
∴ 则关于a,b的二元一次方程组可变形成,
故解为,即
①+②得:3a=6,解得a=2,
代入①得:2+b=1,解得:b=-1.
故方程组的解为:
故答案为:.
观察发现两个方程为同解方程,故可根据第一个方程的解得到第二个方程的解,再求解即可.
23.
解:由题意可得,
解得,
∴关于m、n的二元一次方程组的解为.
由题意可得,求出m、n的值,据此可得方程组的解.
24.0
解:
,
∵结果不含x的二次项,
∴,
∴.
故答案为:0.
先根据多项式乘以多项式的运算法则展开,再根据结果不含x的二次项可得x的二次项系数为0,然后对所求式子变形,整体代入计算即可.
25.125
解:∵,
∴,
∴.
故答案为:125.
先求出,再根据同底数幂的乘法的法则进行计算即可.
26.1
解:,
由①得③,
把③代入②得:,
解得:,
,
∴
故答案为:1.
利用代入消元法,解二元一次方程组,进而得出的值.
27.4
解:∵是由沿向右移动得到的,
∴,
∴.
故答案为:4.
根据平移的性质可得到,然后计算即可.
28.①③④
解:设AB与DE的交点为F
∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,故①正确;
∵∠2=45°,∠E=60°,
∴∠EFB=∠E+∠2=105°,
∴∠EFB≠∠CAB,
∴AC与DE不平行,故②错误;
∵∠4=∠B=45°,∠C=45°,
∴∠4=∠C,
∴AC∥DE,故③正确;
当∠1=15°时, ∠2=90°-15°=75°,
∴∠EFB=∠E+∠2=60°+75°=135°.
∵∠B=45°,
∴∠B+∠EFB=180°,
∴BC∥DE,故④正确.
综上可得:①③④正确.
故答案为:①③④.
设AB与DE的交点为F,根据同角的余角相等可判断①;由外角的性质可得∠EFB=∠E+∠2=105°,根据平行线的判定定理可判断②;根据∠4=∠B=45°,∠C=45°可得∠4=∠C,根据平行线的判定定理可判断③;由余角的性质可得 ∠2=90°-∠1=75°,根据外角的性质可得∠EFB=∠E+∠2=60°+75°=135°,则∠B+∠EFB=180°,据此判断④.
29.2
解:∵22=4,
∴4的算术平方根是2.
故答案为:2.
依据算术平方根的定义求解即可.
30.7
解:∵把线段AB平移得到线段CD,其中点A的对应点为C,且点A(0,1),C(3,5)
∴0+3=3,1+4=5,
∴把线段AB向上平移4个单位,向右平移3个单位得到线段CD,
∵点B与点D是对应点,且 B(a、c),D(c,d),
∴a+3=c,c+4=b,
∴a=c-3,b=c+4,
∴b-a=c+4-(c-3)=4+3=7.
故答案为:7.
根据横坐标,右移加,左移减;纵坐标,上移加,下移减先求出平移的方向和单位,即可求解.
31.
解:2x2-x.
故答案为:2x2-x.
利用单项式乘多项式法则“单项式乘以多项式,就是用单项式去乘以多项式的每一项,再把所得的积相加”将原式展开即可.
32.-1;0
解:∵m2=2n+1①,4n2=m+1②(m≠2n) ,
①-②得:m2-4n2=2n-m,
∴(m+2n)(m-2n)=2n-m,
∵m≠2n,
∴2n-m≠0,
∴m+2n=-1.
∵ 4n2=m+1 ,
∴ 4n3=mn+n ,2n2=(m+1),
∴ 4n3﹣mn+2n2=mn+n -mn+(m+1)=n+m+=(m+2n) +=×(-1)+=0
故答案为:-1,0.
(1)将两等式相减可得m2-4n2=2n-m,再利用平方差公式变形,从而求解;
(2) 由4n2=m+1 可求4n3=mn+n ,2n2=(m+1),然后代入待求式子整理化简,再整体代入计算即可.
33.45
解:如图,过点D作DG⊥BC于点G,
设∠CDE=α,∠FDG=β,
∴根据折叠性质得∠GDE=∠CDE=α,∠ADF=∠FDC,
∴∠FDC=∠ADF=∠FDG+∠GDE+∠CDE=β+α+α=β+2α,
∵四边形ABGD是矩形,
∴∠ADG=90°,
∴∠AGD=∠ADF+∠FDG=β+2α+β=90°,
∴β+α=45°,
∴折痕DE、DF所成的角为∠FDE=β+α=45°.
故答案为:45.
过点D作DG⊥BC于点G,设∠CDE=α,∠FDG=β,根据折叠的性质得∠GDE=∠CDE=α,∠ADF=∠FDC,从而求出∠ADF=β+2α,再根据矩形的性质求出β+α=45°后即可得到答案.
34.5
解:设小长方形的长为x,宽为y,
根据题意得:20+y-x=10+x-y,
即2x-2y=20-10,
整理得:,
小长方形的长与宽的差是5,
故答案为:5.
设小长方形的长为x,宽为y,根据两种不同的摆放方式分别表示出长方形课本的长,进而根据长方形课本的长不变列出方程,求出x-y的值即可.
35. 2x(x+2)(x﹣2)
解:2x3﹣8x=2x(x2﹣4)=2x(x+2)(x﹣2).
故答案为:2x(x+2)(x﹣2).
先提公因式2x,分解成2x(x2﹣4),而x2﹣4可利用平方差公式分解.
36.1
解: ∵,
∴xy=axy,
∴a=1.
故答案为:1.
利用完全平方公式将等式左边展开,利用等式对应项系数相等即可求解.
37.PC;垂线段最短
解:如图,直线l表示一段河道,现要从河道l向村庄P引水,现有PA,PB,PC,PD四条水渠,其中长度最短的水渠是线段PC,理由是垂线段最短.
故答案为:PC,垂线段最短.
根据从直线外一点,到直线上任意一点所引的线段中,垂直线段最短进行求解即可.
38.1
解:∵
∴
解得:,
∴,
故答案为:.
根据绝对值和偶次方的非负性得出关于x,y的二元一次方程组,解方程组求出x,y,然后计算即可.
39.43°
解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠4,∠AEF=∠2,
∵ EG是的角平分线,
∴∠2=∠AEF=2∠4,
∵∠2+∠4=129°,
∴3∠4=129°,
∴∠4=43°,
∴∠3=43°.
故答案为:43°.
由同位角相等,两直线平行,可得AB∥CD,利用两直线平行,内错角相等可得∠3=∠4,∠AEF=∠2,再由角平分线的定义可得∠2=∠AEF=2∠4,结合∠2+∠4=129°可求出∠4的度数,继而得解.
40.72°
解:∵ ∠1=∠2 ,
∴a∥b(内错角相等,两直线平行),
∴∠3+∠4=180°(二直线平行,同旁内角互补),
∵∠3=108°,
∴∠4=180°-108°=72°.
故答案为:72°.
由内错角相等,两直线平行得a∥b,由二直线平行,同旁内角互补得∠3+∠4=180°,再代入∠3的度数即可求出∠4的度数.
41.
解:∵( )2=3,
∴3的平方根是为 .
故答案为:± .
直接根据平方根的概念即可求解.
42.垂线段最短
解:∵PB⊥AD,垂足点为B,
∴沿线路PB行走距离最短,其依据的几何学原理是垂线段最短.
故答案为:垂线段最短.
根据垂线段最短的性质,即可得到答案.
43.;;
解:当时,,
∵,
∴,
∴这是一个假命题.
故答案为:、、.
举例说明一个命题是假命题的反例,需要满足命题的题设,不满足命题的结论,据此解答即可.
44.
解:如图,
∵∠1=160°,∠C=90°,
∴∠3=∠1-∠C=70°,
∴∠2=∠3=70°.
故答案为:70°.
根据三角形的外角性质得到∠3=∠1-∠C=70°,再根据对顶角相等得到∠2=∠3,即可得到答案.
45.
解:设有x个老人,y个梨,
根据题意可列方程:.
故答案为:.
设有x个老人,y个梨,根据“ 一人一个多一梨”可列方程x+1=y,根据“ 一人两个少二梨 ”可列方程2x-2=y,联立两方程,即可得到答案.
46.①②③
解:①∵ 线段CD是由线段AB平移所得,
∴AD//BC,故①正确;
②∵AD//BC,AB//CD,
∴∠ADC+∠DAB=180°,∠DAB+∠ABC=180°,
∴∠ADC=∠ABC,故②正确;
③∵,
∴,
∴,故③正确;
④ 根据题意可知,线段CD是由线段AB向右平移2个单位,再向上平移2个单位得到,
∵A(-3,0),
∴D(-1,2),故④错误;
综上所述,①②③正确.
故答案为:①②③.
根据平移的性质可得AD//BC,AB//CD,据此可判断①;再根据二直线平行,同旁内角互补可得∠ADC+∠DAB=180°,∠DAB+∠ABC=180°,由同角的补角相等得∠ADC=∠ABC,据此可判断②;根据点的坐标与图形的性质、三角形面积公式及平移的性质可对③进行判断;根据点的坐标平移规律“横坐标左移减右移加,纵坐标上移加下移减”可对④进行判断.
同课章节目录
