2024-2025学年浙教版七年级数学下册期中真题专项复习10填空题(含答案)(浙江专用)
文档属性
| 名称 | 2024-2025学年浙教版七年级数学下册期中真题专项复习10填空题(含答案)(浙江专用) |  | |
| 格式 | docx | ||
| 文件大小 | 470.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 21:41:19 | ||
图片预览


文档简介
2024-2025学年七年级数学下册期中真题专项复习10填空题
1.(2024七下·临平期中)已知,用含的代数式表示,则 .
2.(2024七下·余姚期中)如图AB∥CD,AE交DF于点C,∠ECF=134°,则∠A=
3.(2024九上·崆峒期中)因式分解 = .
4.(2024七下·鄞州期中) 在中,用含的代数式表示,则 .
5.(2024七下·阳西期末) 已知方程,用含x的代数式表示y,那么 .
6.(2024七下·浙江期中)已知方程2x+y=5,若用含x的代数式表示y,则y= .
7.(2024七下·宁波期中) 写一个解为的二元一次方程 .
8.(2024七下·余姚期中)若,则
9.(2024七下·吴兴期中) 如图,,平分,,则 度.
10.(2024七下·宁波期中) 如图,将一条两边沿互相平行的纸带折叠,设°,则 (用关于x的代数式表示)
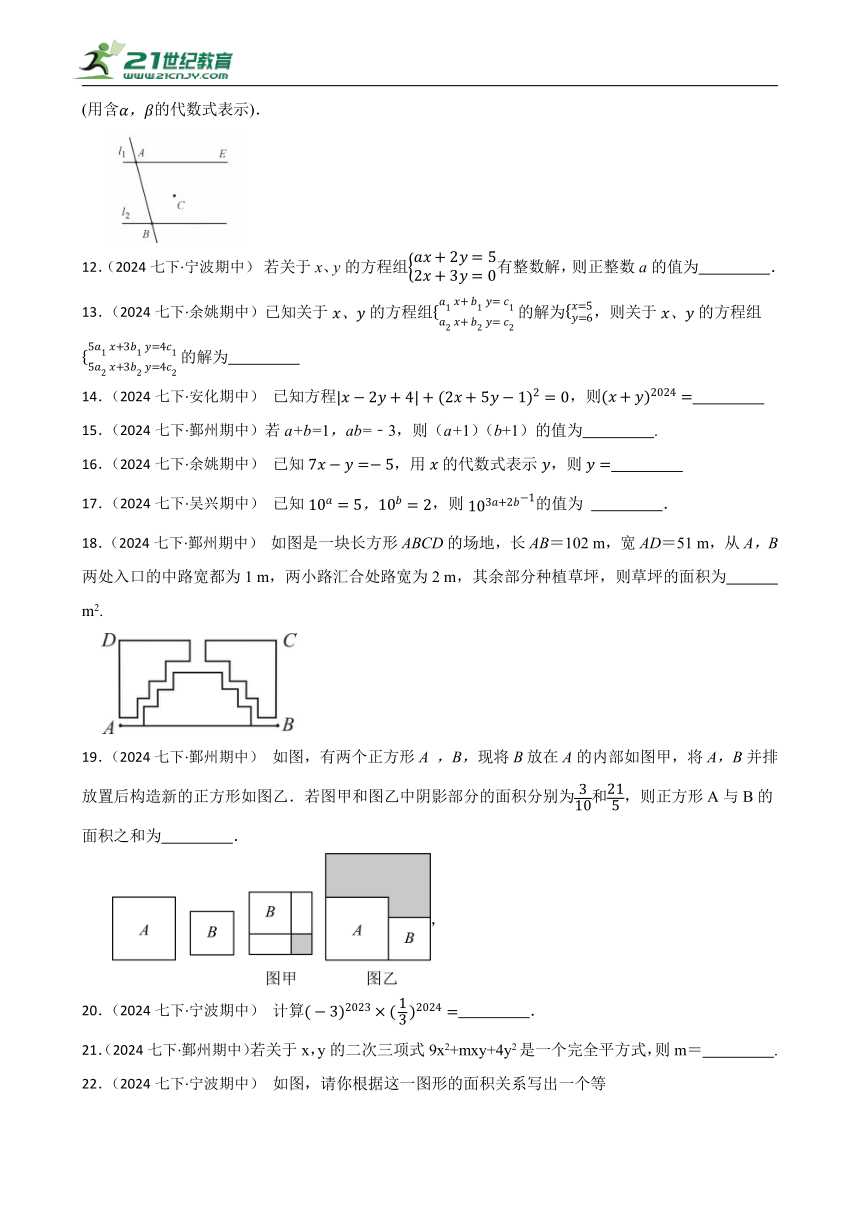
11.(2024七下·浙江期中)如图,两条平行直线被直线所截,点位于两平行线之间,且在直线右侧,点是上一点,位于点右侧.小明进行了如下操作:连结,在平分线上取一点,过点作,交直线于点.记,则 (用含的代数式表示).
12.(2024七下·宁波期中) 若关于x、y的方程组有整数解,则正整数a的值为 .
13.(2024七下·余姚期中)已知关于的方程组的解为,则关于的方程组的解为
14.(2024七下·安化期中) 已知方程,则
15.(2024七下·鄞州期中)若a+b=1,ab=﹣3,则(a+1)(b+1)的值为 .
16.(2024七下·余姚期中) 已知,用的代数式表示,则
17.(2024七下·吴兴期中) 已知,则的值为 .
18.(2024七下·鄞州期中) 如图是一块长方形ABCD的场地,长AB=102 m,宽AD=51 m,从A,B两处入口的中路宽都为1 m,两小路汇合处路宽为2 m,其余部分种植草坪,则草坪的面积为 m2.
19.(2024七下·鄞州期中) 如图,有两个正方形A ,B,现将B放在A的内部如图甲,将A,B并排放置后构造新的正方形如图乙.若图甲和图乙中阴影部分的面积分别为和,则正方形A与B的面积之和为 .
,
20.(2024七下·宁波期中) 计算 .
21.(2024七下·鄞州期中)若关于x,y的二次三项式9x2+mxy+4y2是一个完全平方式,则m= .
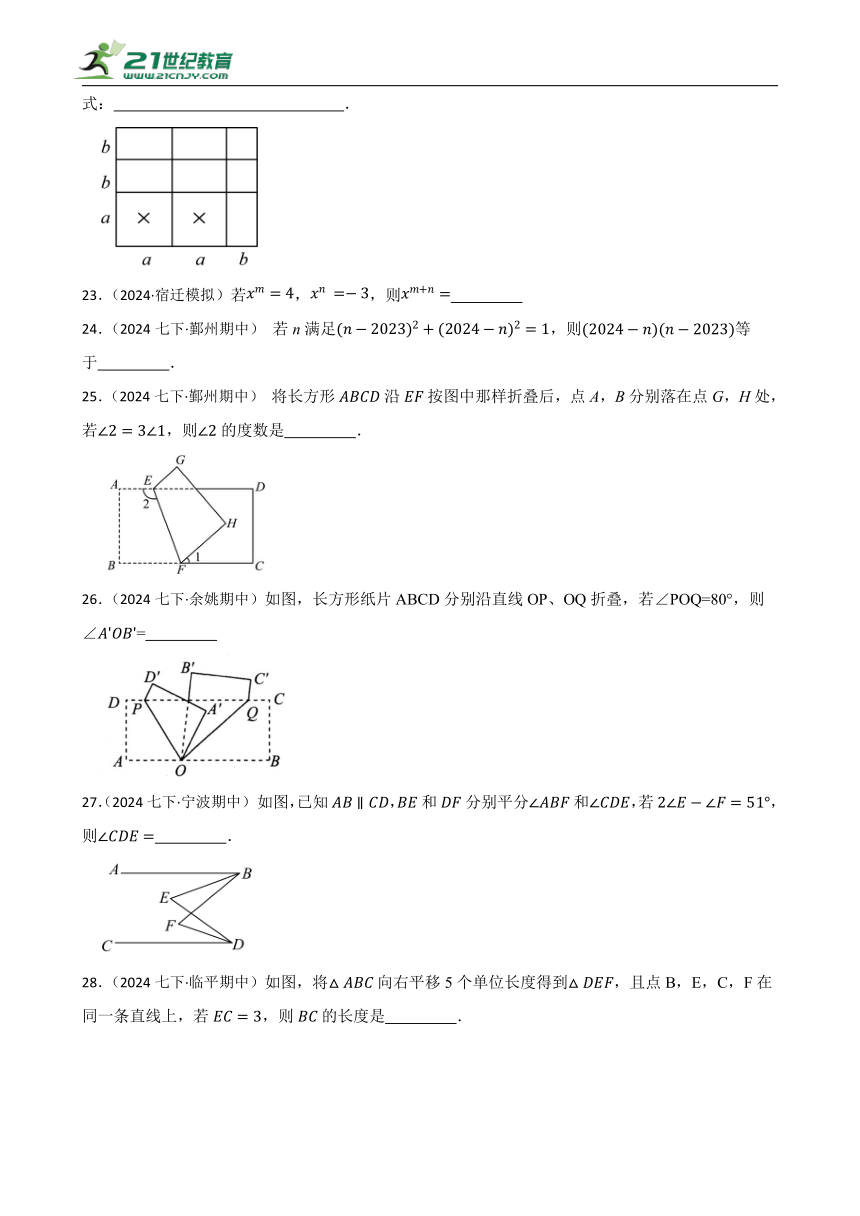
22.(2024七下·宁波期中) 如图,请你根据这一图形的面积关系写出一个等式: .
23.(2024·宿迁模拟)若,,则
24.(2024七下·鄞州期中) 若n满足,则等于 .
25.(2024七下·鄞州期中) 将长方形沿按图中那样折叠后,点A,B分别落在点G,H处,若,则的度数是 .
26.(2024七下·余姚期中)如图,长方形纸片ABCD分别沿直线OP、OQ折叠,若∠POQ=80°,则∠=
27.(2024七下·宁波期中) 如图,已知,和分别平分和,若,则 .
28.(2024七下·临平期中)如图,将向右平移5个单位长度得到,且点B,E,C,F在同一条直线上,若,则的长度是 .
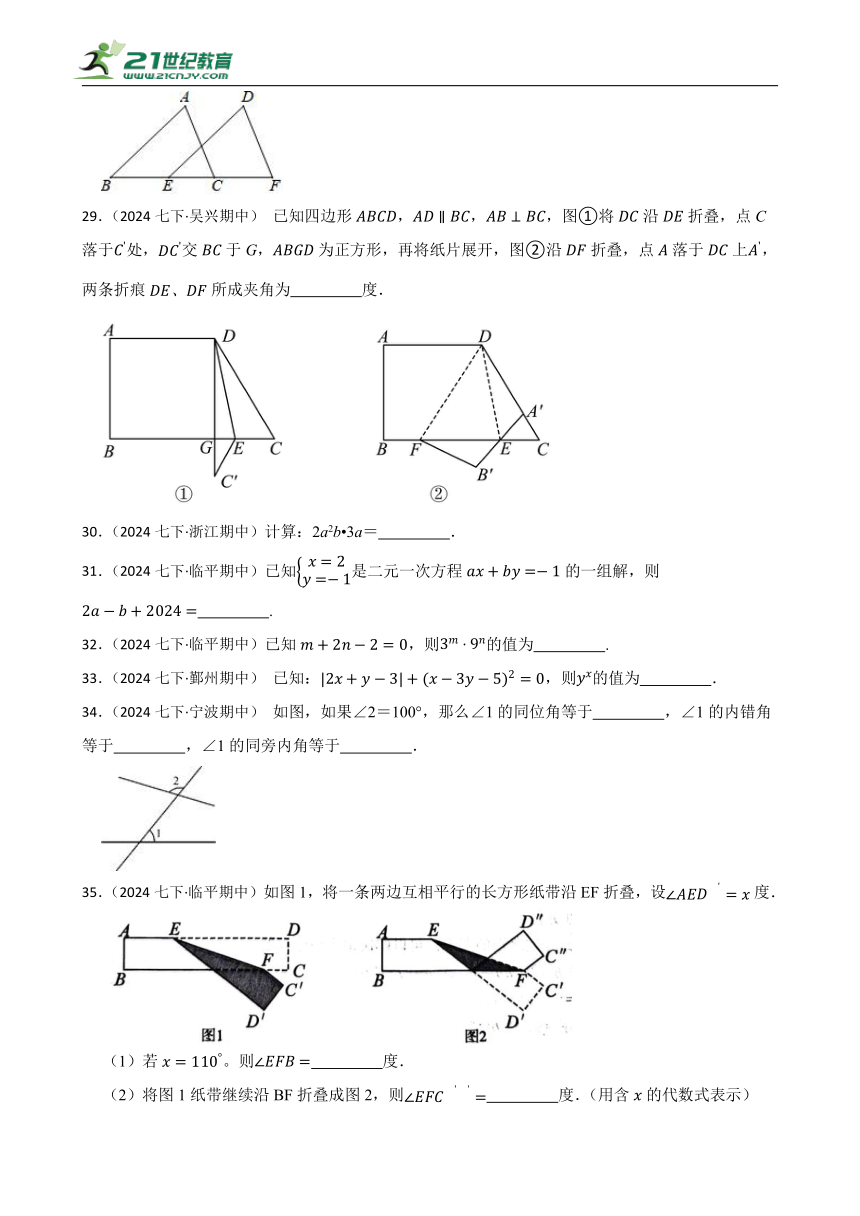
29.(2024七下·吴兴期中) 已知四边形,,,图①将沿折叠,点C落于处,交于G,为正方形,再将纸片展开,图②沿折叠,点落于上,两条折痕所成夹角为 度.
30.(2024七下·浙江期中)计算:2a2b 3a= .
31.(2024七下·临平期中)已知是二元一次方程的一组解,则 .
32.(2024七下·临平期中)已知,则的值为 .
33.(2024七下·鄞州期中) 已知:,则的值为 .
34.(2024七下·宁波期中) 如图,如果∠2=100°,那么∠1的同位角等于 ,∠1的内错角等于 ,∠1的同旁内角等于 .
35.(2024七下·临平期中)如图1,将一条两边互相平行的长方形纸带沿EF折叠,设度.
(1)若。则 度.
(2)将图1纸带继续沿BF折叠成图2,则 度.(用含的代数式表示)
36.(2024八上·简阳月考)分解因式:= .
37.(2024七下·杭州期中)如图,将一条长方形纸片沿AB折叠,已知∠DAB=70°,则∠CBF= .
38.(2024七下·鄞州期中) 若是方程的一组解,则 .
39.(2024七下·浙江期中)已知关于x,y的二元一次方程组 的解为 ,则关于n,y的二元一次方程组 的解为 .
40.(2024七下·临平期中)若 ,则 .
41.(2024七下·浙江期中)如图,将三角形平移得到三角形,若图中阴影部分面积与所有空白部分面积之比为,则阴影部分面积与三角形面积的比值为
42.(2024七下·宁波期中) 计算 .
答案解析部分
1.5b+2
解:由等式的性质得a=2+5b
故答案为:5b+2.
直接由等式的性质进行移项便可得结果.
2.
解:∵ ∠ECF=134° ,
∴∠FCA=180°- ∠ECF=46°,
∵AB∥CD,
∴∠A=∠FCA=46°.
故答案为:46°.
先根据邻补角算出∠FCA的度数,进而根据二直线平行,内错角相等得∠A=∠FCA,从而得出答案.
3.
解:原式 ,
故答案为: .
观察此多项式的特点:两项都含有公因式a,由此利用提取公因式法分解因式.
4.
解:移项得,
将x系数化为1得:,
故答案为:.
移项后把x系数化为1即可.
5.
解:移项得,
∴.
故答案为:.
移项后,把y的系数化为1即可.
6.5﹣2x
解:由等式的性质,原方程左右两边同时减去2x得y=5-2x.
故答案为:5-2x.
将不含y的项移到方程的一边即可.
7.(答案不唯一)
解:设x+ay=5
把 代入得:
解得:a=-1.
故方程为:
故答案为:(答案不唯一)
根据题意可设方程为x+ay=5,代入解,求得a,即可得到方程,设的方程不唯一,最终结果也不唯一.
8.
解:∵(x+m)(x+3)=x2+(3+m)x+3m=x2+nx+6,
∴3+m=n,3m=6,
∴m=2,n=5,
∴.
故答案为:.
首先根据多项式乘以多项式法则将已知等式的左边展开,然后根据对应项的系数相等可得3+m=n,3m=6,求解得出m、n的值,从而即可求出m与n的比值.
9.70
解:∵,
∴,,
∵平分,
∴,
故答案为:.
根据平行线的性质可得,,再由角平分线的定义求出∠DCE即可.
10.
解:延长AE到H,如图所示:
由题意得:AE//BC,EF//GC.
∴∠FEA=∠1=x°.
由折叠得:∠CEH=∠CEF=∠2+∠FEA.
又∵∠2+∠CEH=180°,
∴∠2+∠2+x°=180°,
解得:
故答案为:
根据平行线的性质可得∠FEA=∠1=x°. 再根据邻补角的定义和折叠的性质可得∠2+∠2+x°=180°,求解即可得到∠2.
11.或或
解:解:设∠DAE=θ,
∵AD平分∠EAC,
∴∠CAD=∠DAE=θ,∠CAE=2∠EAD=2θ,
①当点F在B的右侧,且D在12上方时,过点C作CM∥l1,如图1所示:
∵l1∥l2,
∴l1∥CM∥l2,
∴∠EAC=∠ACM,∠CBF=∠BCM,
又∵∠ACB=∠ABM+∠BCM,
∴∠ACB=∠CAE+∠CBF,
同理:∠D=∠DAE+∠DFN,
∵DF∥BC,
∴∠DFN=∠CBF,
∵∠ACB=α,∠CBF=β,∠ADF=γ,
∴α=2θ+β,γ=θ+β,
由γ=θ+β,得:θ=γ-β,
将θ=γ-β代入α=2θ+β,得:α=2(γ-β)+β,
∴;
②当点F在B的左侧时,且D在12上方时,如图2所示:
同理:∠ACB=∠CAE+∠CBN,∠D=∠DAE+∠DFN,
∵∠DFN=∠CBN=180°-∠CBF=180°-β,
∴α=2θ+180°-β,γ=θ+180°-β,
由γ=θ+180°-β,得:θ=γ+β-180°,
将θ=γ+β-180°代入α=2θ+180°-β,得:;
③当点D在直线l2的下方时,过点点D作TK∥l1,如图3所示:
同理:∠ACB=∠CAE+∠CBF,
即α=2θ+β,
∵TK∥l1,l1∥l2,
∴l1∥l2∥TK,
∴∠ADT=∠DAE=θ,∠FDK=∠BFD=∠CBF=β,
∵∠ADT+∠ADF+∠FDK=180°,
∴θ+γ+β=180°,
∴θ=180°-γ-β,
将θ=180°-γ-β代入α=2θ+β,得:α=2(180°-γ-β)+β,
∴;
综上所述:或或;
故答案为: 或或.
设∠DAE=θ,则∠CAD=∠DAE=θ,∠CAE=2∠EAD=2θ,①当点F在B的右侧,且D在12上方时,过点C作CM∥l1,根据两直线平行,内错角相等可推得∠ACB=∠CAE+∠CBF,同理可得∠D=∠DAE+∠DFN,则α=2θ+β,γ=θ+β,由此可得出γ的度数;②当点F在B的左侧时,且D在12上方时,根据两直线平行,内错角相等可推得∠ACB=∠CAE+∠CBF,∠D=∠DAE+∠DFN,则α=2θ+β,γ=θ+β,由此可得出γ的度数;③当点D在直线l2的下方时,过点点D作TK∥l1,根据两直线平行,内错角相等可得∠ADT=∠DAE=θ,∠FDK=∠BFD=∠CBF=β,推得∠ACB=∠CAE+∠CBF,则α=2θ+β,根据∠ADT+∠ADF+∠FDK=180°得θ+γ+β=180°,由此可得出γ的度数.
12.1或3
解:
①×3-②×2,得:3ax-4x=15.
解得:.
把代入②得:
∵方程组有整数解,
∴3a-4是15和10的公因数,
∴3a-4=±1,±5,
当3a-4=1,,
当3a-4=-1,a=1,
当3a-4=5,a=3,
当3a-4=-5,.
∵a取正整数,
∴a的值为 1或3.
当故答案为:1或3.
先解方程,求出x和y,根据方程有整数解,知道x和y的分母是两个分子的公分母,从而可得关于a的方程,分别解方程即可.
13.
解:∵可以变形为:,
又∵的解为,
∴,
解得.
故答案为:.
将第二个方程组变形为,从而对照第一个方程组的解可得,求解即可得出第二个方程组的解.
14.1
解:∵
∴
解得:,
∴,
故答案为:.
根据绝对值和偶次方的非负性得出关于x,y的二元一次方程组,解方程组求出x,y,然后计算即可.
15.-1
解:∵,
∴
,
故答案为:.
根据多项式乘以多项式的运算法则展开,然后整体代入计算即可.
16.
解:7x-y=-5,
移项,的7x+5=y,
∴y=7x+5.
故答案为:7x+5.
将字母x作为已知数,然后利用移项,将不含y的项移到方程的一边即可.
17.50
解:,
,
故答案为:50.
逆用同底数幂的乘除法,幂的乘方法则计算即可.
18.5000
解:由图可得,草坪部分正好可以拼成一个长方形,
且这个长方形的长为102 2=100m,宽为51 1=50m,
所以草坪的面积为
故答案为:5000.
草坪部分正好可以拼成一个长方形,求出长方形的长和宽,然后计算即可.
19.4.5
解:设A、B正方形的边长分别为a、b,则面积分别为,
由图甲得:,
由图乙得:,
∴,
∴.
故答案为:.
设A、B正方形的边长分别为a、b,则面积分别为,根据图中阴影部分的面积列式整理得到,,然后利用完全平方公式计算即可.
20.
解:
故答案为:
先将变形成,再利用积的平方的逆运算进行计算即可.
21.±12
解:由题意得9x2+mxy+4y2=(3x±2y)2=9x2+±12xy+4y2.
∴m=±12.
故答案为±12.
多项式可变形为(3x)2+mxy+(2y)2,结合完全平方式可得m的值.
22.
解:大长方形的长:2a+b,宽:2b+a,故面积可表示为:(2a+b)(2b+a);
大长方形的面积也可表示为每个小图形的面积和,即:5ab+2b2+2a2;
故可得等式:(2a+b)(2b+a)=5ab+2b2+2a2.
故答案为:(2a+b)(2b+a)=5ab+2b2+2a2.
根据题意可得大长方形的两种面积表示方法,即可得到关于面积的等式.
23.12
解:∵xm=4,xn=-3,
∴xm+n=xmxn=4×(-3)=-12.
故答案为:-12.
由同底数幂的乘法法则的逆用将待求式子变形后整体代入,按有理数的乘法法则计算即可.
24.0
解:∵,
∴,
∴,
∴,
∴,
故答案为:.
利用完全平方公式变形,可得,进而可得答案.
25.108°
解:由折叠可得:,
∵,
∴,
∵四边形是长方形,
∴,
∴,
∴,
∵,
∴,
解得:,
∴.
故答案为:.
由折叠的性质可得,再结合平角的定义可得:,再由平行线的性质可得,从而可求解.
26.20°
解:由折叠的性质得∠AOP=∠A'OP,∠BOQ=∠B'OQ,
∵∠AOP+∠POQ+∠BOQ=180°,∠POQ=80°,
∴∠AOP+∠BOQ=100°,
∴∠A'OP+∠B'OQ=100°,
∴∠A'OB'=∠A'OP+∠B'OQ-∠POQ=20°.
故答案为:20°.
由折叠的性质得∠AOP=∠A'OP,∠BOQ=∠B'OQ,由平角的定义得∠AOP+∠BOQ=100°,则∠A'OP+∠B'OQ=100°,进而根据∠A'OB'=∠A'OP+∠B'OQ-∠POQ可算出答案.
27.
解:延长DE交AB于点N,延长BF交CD于点M,如图所示:
∴∠NBE+∠BNE=∠BED,∠MDF+∠DMF=∠BFD.
∵和分别平分和,
∴∠NBF=2∠NBE,∠MDE=2∠MDF.
∵AB∥CD,
∴∠BNE=∠MDE,∠NBF=∠DMF.
∵
∴2(∠NBE+∠BNE)-(∠MDF+∠DMF)
∴∠CDE=∠MDE=34°.
故答案为:
根据三角形外角性质可得∠NBE+∠BNE=∠BED,∠MDF+∠DMF=∠BFD.根据平行线的性质可得∠BNE=∠MDE,∠NBF=∠DMF.根据角平分线的性质得∠NBF=2∠NBE,∠MDE=2∠MDF.最后代入 ,并进行等量代换,即可得到关于∠MDE的方程,求解即可.
28.8
解:∵ 将△ABC向右平移5个单位长度得到△DEF,
∴BE=CF=5,
∵ 点B,E,C,F在同一条直线上,且EC=3,
∴BC=BE+EC=5+3=8.
故答案为:8.
根据平移的性质得BE=CF=5,进而根据BC=BE+EC计算即可.
29.45
解:如图,过作于点,
设,,
由折叠可得,,
∵四边形是正方形,
∴,
∴,
∴.
故答案为:45.
过作于,设,,
由折叠得到,,根据得到,然后求出x+y即可.
30.6a3b
解: 2a2b 3a=(2×3)(a2 a)b=6a3b,
故答案为:6a3b.
根据单项式乘单项式的规则“单项式乘以单项式,把系数与相同字母分别相乘,对于只在某一个单项式含有的字母,则连同指数作为积的一个因式”进行计算即可.
31.2023
解:将x=1,y=-1代入方程可得2a-b=-1,于是2a-b+2024=-1+2024=2023
故答案为:2023.
将解代入方程再进行整体代换可得结果.
32.9
解:由已知得m+2n=2,同时3m ·9n=3m ·32n=3m+2n=32=9
故答案为:9.
将9n化为以3为底的幂,即可运用同底数幂运算的规则进行计算.
33.1
解:∵,
∴,
解得:
∴.
故答案为:1.
根据非负数的性质得到关于x,y的方程组,解方程组求出x,y,然后根据乘方的运算法则计算即可.
34.80°;80°;100°
解:如图所示:
由图可得,∠1的同位角是∠EGB,∠1的内错角是∠AGF,∠1的同旁内角是∠BGF,
∵∠2=100°,∠2+∠EGB=180°,∠2=∠BGF.
∴∠AGF=EGB=180°-∠2=80°,∠BGF=100°.
∴ ∠1的同位角等于80°,∠1的内错角等于80°,∠1的同旁内角等于100°.
故答案为:80°;80°;100°.
根据图形分析出∠1的同位角,内错角和同旁内角,然后根据这三个角和∠2的关系分别求值即可.
35.(1)35
(2)
解:(1)∠AED'+∠DED'=180°得∠DED'=70°,由折叠可知∠DEF=∠D'EF,故∠DEF=35°,又由AD||BC得∠EFB=∠DEF=35°
故填:35°.
(2)由图(1),AD||BC得∠FED'=∠EFB=12(1800-x)=90°-12x,
而CF'||D'E得∠EFC'+∠FED'=180得∠EFC'=180°-(90°-12x)=90°+12x ,
得∠BFC'=∠EFC'-∠EFB=90°+12x-(90°-12x)=x
由折叠可知∠BFC''=∠BFC'=x,而∠EFC''=∠BFC''-∠EFB=x-(90°-12x)=32x-90°
故填:.
直接由折叠的性质得到∠DEF的度数,再由平行内错角相等可得∠EFB的度数.而(2)问中需要反复利用平行的性质与折叠的性质进行导角.
36.
解:由题意得,
故答案为:
根据提公因式法、公式法进行因式分解,进而即可求解。
37.40°
解:如图,
∵AD||BC,
∴∠1=∠DAB=70°,
由折叠的性质知∠2=∠1=70°,
∴故∠CBF=180°-∠1-∠2=180°-70°-70°=40°,
故答案为:40°.
由二直线平行,内错角相等,可得∠1的度数,由折叠的性质可得∠1=∠2,进而根据平角定义即可求得∠CBF的度数.
38.2014
解:∵是方程的一组解,
∴,
∴,
故答案为:2014.
根据二元一次方程的解的定义可得,然后对所求式子变形,整体代入计算即可.
39.
解:关于x、y的方程组 可化为,
与关于x、y的方程组为同解方程组,
根据整体换元可知
解得.
故答案为:.
整体法观察两个方程为同解方程,整体换元即可求解x、y的值.
40.-2
解:∵(x+3)(x 5)= x2 5x+3x 15=x2 2x 15,
∴m= 2.
故答案为: 2.
根据多项式与多项式的乘法法则将左式展开并合并同类项,然后根据多项式的性质可得m的值.
41.
解:由平移的性质得△ABC≌△A'B'C',
∴S△ABC=S△A'B'C',
设三角形ABC中空白面积为S上,三角形A'B'C'中空白面积为S下,
∴S上=S△ABC-S阴影,S下=S△A'B'C'-S阴影,
∴S上=S下,
∵阴影部分面积与所有空白部分面积之比为1:6,
∴设阴影部分面积为x,则所有空白部分面积为6x,
∴S上=3x,
∴S△ABC=S上+S阴影=3x+x=4x,
∴阴影部分面积与三角形ABC面积的比值为;
故答案为:.
根据平移可得△ABC与△A'B'C'的面积相等,推得上、下两个空白部分面积相等,结合已知条件即可求出阴影部分面积与三角形ABC面积的比值.
42.
解:
=.
故答案为:.
多项式÷单项式,用多项式的每一项去除单项式,并把所得的结果相加即可.
1.(2024七下·临平期中)已知,用含的代数式表示,则 .
2.(2024七下·余姚期中)如图AB∥CD,AE交DF于点C,∠ECF=134°,则∠A=
3.(2024九上·崆峒期中)因式分解 = .
4.(2024七下·鄞州期中) 在中,用含的代数式表示,则 .
5.(2024七下·阳西期末) 已知方程,用含x的代数式表示y,那么 .
6.(2024七下·浙江期中)已知方程2x+y=5,若用含x的代数式表示y,则y= .
7.(2024七下·宁波期中) 写一个解为的二元一次方程 .
8.(2024七下·余姚期中)若,则
9.(2024七下·吴兴期中) 如图,,平分,,则 度.
10.(2024七下·宁波期中) 如图,将一条两边沿互相平行的纸带折叠,设°,则 (用关于x的代数式表示)
11.(2024七下·浙江期中)如图,两条平行直线被直线所截,点位于两平行线之间,且在直线右侧,点是上一点,位于点右侧.小明进行了如下操作:连结,在平分线上取一点,过点作,交直线于点.记,则 (用含的代数式表示).
12.(2024七下·宁波期中) 若关于x、y的方程组有整数解,则正整数a的值为 .
13.(2024七下·余姚期中)已知关于的方程组的解为,则关于的方程组的解为
14.(2024七下·安化期中) 已知方程,则
15.(2024七下·鄞州期中)若a+b=1,ab=﹣3,则(a+1)(b+1)的值为 .
16.(2024七下·余姚期中) 已知,用的代数式表示,则
17.(2024七下·吴兴期中) 已知,则的值为 .
18.(2024七下·鄞州期中) 如图是一块长方形ABCD的场地,长AB=102 m,宽AD=51 m,从A,B两处入口的中路宽都为1 m,两小路汇合处路宽为2 m,其余部分种植草坪,则草坪的面积为 m2.
19.(2024七下·鄞州期中) 如图,有两个正方形A ,B,现将B放在A的内部如图甲,将A,B并排放置后构造新的正方形如图乙.若图甲和图乙中阴影部分的面积分别为和,则正方形A与B的面积之和为 .
,
20.(2024七下·宁波期中) 计算 .
21.(2024七下·鄞州期中)若关于x,y的二次三项式9x2+mxy+4y2是一个完全平方式,则m= .
22.(2024七下·宁波期中) 如图,请你根据这一图形的面积关系写出一个等式: .
23.(2024·宿迁模拟)若,,则
24.(2024七下·鄞州期中) 若n满足,则等于 .
25.(2024七下·鄞州期中) 将长方形沿按图中那样折叠后,点A,B分别落在点G,H处,若,则的度数是 .
26.(2024七下·余姚期中)如图,长方形纸片ABCD分别沿直线OP、OQ折叠,若∠POQ=80°,则∠=
27.(2024七下·宁波期中) 如图,已知,和分别平分和,若,则 .
28.(2024七下·临平期中)如图,将向右平移5个单位长度得到,且点B,E,C,F在同一条直线上,若,则的长度是 .
29.(2024七下·吴兴期中) 已知四边形,,,图①将沿折叠,点C落于处,交于G,为正方形,再将纸片展开,图②沿折叠,点落于上,两条折痕所成夹角为 度.
30.(2024七下·浙江期中)计算:2a2b 3a= .
31.(2024七下·临平期中)已知是二元一次方程的一组解,则 .
32.(2024七下·临平期中)已知,则的值为 .
33.(2024七下·鄞州期中) 已知:,则的值为 .
34.(2024七下·宁波期中) 如图,如果∠2=100°,那么∠1的同位角等于 ,∠1的内错角等于 ,∠1的同旁内角等于 .
35.(2024七下·临平期中)如图1,将一条两边互相平行的长方形纸带沿EF折叠,设度.
(1)若。则 度.
(2)将图1纸带继续沿BF折叠成图2,则 度.(用含的代数式表示)
36.(2024八上·简阳月考)分解因式:= .
37.(2024七下·杭州期中)如图,将一条长方形纸片沿AB折叠,已知∠DAB=70°,则∠CBF= .
38.(2024七下·鄞州期中) 若是方程的一组解,则 .
39.(2024七下·浙江期中)已知关于x,y的二元一次方程组 的解为 ,则关于n,y的二元一次方程组 的解为 .
40.(2024七下·临平期中)若 ,则 .
41.(2024七下·浙江期中)如图,将三角形平移得到三角形,若图中阴影部分面积与所有空白部分面积之比为,则阴影部分面积与三角形面积的比值为
42.(2024七下·宁波期中) 计算 .
答案解析部分
1.5b+2
解:由等式的性质得a=2+5b
故答案为:5b+2.
直接由等式的性质进行移项便可得结果.
2.
解:∵ ∠ECF=134° ,
∴∠FCA=180°- ∠ECF=46°,
∵AB∥CD,
∴∠A=∠FCA=46°.
故答案为:46°.
先根据邻补角算出∠FCA的度数,进而根据二直线平行,内错角相等得∠A=∠FCA,从而得出答案.
3.
解:原式 ,
故答案为: .
观察此多项式的特点:两项都含有公因式a,由此利用提取公因式法分解因式.
4.
解:移项得,
将x系数化为1得:,
故答案为:.
移项后把x系数化为1即可.
5.
解:移项得,
∴.
故答案为:.
移项后,把y的系数化为1即可.
6.5﹣2x
解:由等式的性质,原方程左右两边同时减去2x得y=5-2x.
故答案为:5-2x.
将不含y的项移到方程的一边即可.
7.(答案不唯一)
解:设x+ay=5
把 代入得:
解得:a=-1.
故方程为:
故答案为:(答案不唯一)
根据题意可设方程为x+ay=5,代入解,求得a,即可得到方程,设的方程不唯一,最终结果也不唯一.
8.
解:∵(x+m)(x+3)=x2+(3+m)x+3m=x2+nx+6,
∴3+m=n,3m=6,
∴m=2,n=5,
∴.
故答案为:.
首先根据多项式乘以多项式法则将已知等式的左边展开,然后根据对应项的系数相等可得3+m=n,3m=6,求解得出m、n的值,从而即可求出m与n的比值.
9.70
解:∵,
∴,,
∵平分,
∴,
故答案为:.
根据平行线的性质可得,,再由角平分线的定义求出∠DCE即可.
10.
解:延长AE到H,如图所示:
由题意得:AE//BC,EF//GC.
∴∠FEA=∠1=x°.
由折叠得:∠CEH=∠CEF=∠2+∠FEA.
又∵∠2+∠CEH=180°,
∴∠2+∠2+x°=180°,
解得:
故答案为:
根据平行线的性质可得∠FEA=∠1=x°. 再根据邻补角的定义和折叠的性质可得∠2+∠2+x°=180°,求解即可得到∠2.
11.或或
解:解:设∠DAE=θ,
∵AD平分∠EAC,
∴∠CAD=∠DAE=θ,∠CAE=2∠EAD=2θ,
①当点F在B的右侧,且D在12上方时,过点C作CM∥l1,如图1所示:
∵l1∥l2,
∴l1∥CM∥l2,
∴∠EAC=∠ACM,∠CBF=∠BCM,
又∵∠ACB=∠ABM+∠BCM,
∴∠ACB=∠CAE+∠CBF,
同理:∠D=∠DAE+∠DFN,
∵DF∥BC,
∴∠DFN=∠CBF,
∵∠ACB=α,∠CBF=β,∠ADF=γ,
∴α=2θ+β,γ=θ+β,
由γ=θ+β,得:θ=γ-β,
将θ=γ-β代入α=2θ+β,得:α=2(γ-β)+β,
∴;
②当点F在B的左侧时,且D在12上方时,如图2所示:
同理:∠ACB=∠CAE+∠CBN,∠D=∠DAE+∠DFN,
∵∠DFN=∠CBN=180°-∠CBF=180°-β,
∴α=2θ+180°-β,γ=θ+180°-β,
由γ=θ+180°-β,得:θ=γ+β-180°,
将θ=γ+β-180°代入α=2θ+180°-β,得:;
③当点D在直线l2的下方时,过点点D作TK∥l1,如图3所示:
同理:∠ACB=∠CAE+∠CBF,
即α=2θ+β,
∵TK∥l1,l1∥l2,
∴l1∥l2∥TK,
∴∠ADT=∠DAE=θ,∠FDK=∠BFD=∠CBF=β,
∵∠ADT+∠ADF+∠FDK=180°,
∴θ+γ+β=180°,
∴θ=180°-γ-β,
将θ=180°-γ-β代入α=2θ+β,得:α=2(180°-γ-β)+β,
∴;
综上所述:或或;
故答案为: 或或.
设∠DAE=θ,则∠CAD=∠DAE=θ,∠CAE=2∠EAD=2θ,①当点F在B的右侧,且D在12上方时,过点C作CM∥l1,根据两直线平行,内错角相等可推得∠ACB=∠CAE+∠CBF,同理可得∠D=∠DAE+∠DFN,则α=2θ+β,γ=θ+β,由此可得出γ的度数;②当点F在B的左侧时,且D在12上方时,根据两直线平行,内错角相等可推得∠ACB=∠CAE+∠CBF,∠D=∠DAE+∠DFN,则α=2θ+β,γ=θ+β,由此可得出γ的度数;③当点D在直线l2的下方时,过点点D作TK∥l1,根据两直线平行,内错角相等可得∠ADT=∠DAE=θ,∠FDK=∠BFD=∠CBF=β,推得∠ACB=∠CAE+∠CBF,则α=2θ+β,根据∠ADT+∠ADF+∠FDK=180°得θ+γ+β=180°,由此可得出γ的度数.
12.1或3
解:
①×3-②×2,得:3ax-4x=15.
解得:.
把代入②得:
∵方程组有整数解,
∴3a-4是15和10的公因数,
∴3a-4=±1,±5,
当3a-4=1,,
当3a-4=-1,a=1,
当3a-4=5,a=3,
当3a-4=-5,.
∵a取正整数,
∴a的值为 1或3.
当故答案为:1或3.
先解方程,求出x和y,根据方程有整数解,知道x和y的分母是两个分子的公分母,从而可得关于a的方程,分别解方程即可.
13.
解:∵可以变形为:,
又∵的解为,
∴,
解得.
故答案为:.
将第二个方程组变形为,从而对照第一个方程组的解可得,求解即可得出第二个方程组的解.
14.1
解:∵
∴
解得:,
∴,
故答案为:.
根据绝对值和偶次方的非负性得出关于x,y的二元一次方程组,解方程组求出x,y,然后计算即可.
15.-1
解:∵,
∴
,
故答案为:.
根据多项式乘以多项式的运算法则展开,然后整体代入计算即可.
16.
解:7x-y=-5,
移项,的7x+5=y,
∴y=7x+5.
故答案为:7x+5.
将字母x作为已知数,然后利用移项,将不含y的项移到方程的一边即可.
17.50
解:,
,
故答案为:50.
逆用同底数幂的乘除法,幂的乘方法则计算即可.
18.5000
解:由图可得,草坪部分正好可以拼成一个长方形,
且这个长方形的长为102 2=100m,宽为51 1=50m,
所以草坪的面积为
故答案为:5000.
草坪部分正好可以拼成一个长方形,求出长方形的长和宽,然后计算即可.
19.4.5
解:设A、B正方形的边长分别为a、b,则面积分别为,
由图甲得:,
由图乙得:,
∴,
∴.
故答案为:.
设A、B正方形的边长分别为a、b,则面积分别为,根据图中阴影部分的面积列式整理得到,,然后利用完全平方公式计算即可.
20.
解:
故答案为:
先将变形成,再利用积的平方的逆运算进行计算即可.
21.±12
解:由题意得9x2+mxy+4y2=(3x±2y)2=9x2+±12xy+4y2.
∴m=±12.
故答案为±12.
多项式可变形为(3x)2+mxy+(2y)2,结合完全平方式可得m的值.
22.
解:大长方形的长:2a+b,宽:2b+a,故面积可表示为:(2a+b)(2b+a);
大长方形的面积也可表示为每个小图形的面积和,即:5ab+2b2+2a2;
故可得等式:(2a+b)(2b+a)=5ab+2b2+2a2.
故答案为:(2a+b)(2b+a)=5ab+2b2+2a2.
根据题意可得大长方形的两种面积表示方法,即可得到关于面积的等式.
23.12
解:∵xm=4,xn=-3,
∴xm+n=xmxn=4×(-3)=-12.
故答案为:-12.
由同底数幂的乘法法则的逆用将待求式子变形后整体代入,按有理数的乘法法则计算即可.
24.0
解:∵,
∴,
∴,
∴,
∴,
故答案为:.
利用完全平方公式变形,可得,进而可得答案.
25.108°
解:由折叠可得:,
∵,
∴,
∵四边形是长方形,
∴,
∴,
∴,
∵,
∴,
解得:,
∴.
故答案为:.
由折叠的性质可得,再结合平角的定义可得:,再由平行线的性质可得,从而可求解.
26.20°
解:由折叠的性质得∠AOP=∠A'OP,∠BOQ=∠B'OQ,
∵∠AOP+∠POQ+∠BOQ=180°,∠POQ=80°,
∴∠AOP+∠BOQ=100°,
∴∠A'OP+∠B'OQ=100°,
∴∠A'OB'=∠A'OP+∠B'OQ-∠POQ=20°.
故答案为:20°.
由折叠的性质得∠AOP=∠A'OP,∠BOQ=∠B'OQ,由平角的定义得∠AOP+∠BOQ=100°,则∠A'OP+∠B'OQ=100°,进而根据∠A'OB'=∠A'OP+∠B'OQ-∠POQ可算出答案.
27.
解:延长DE交AB于点N,延长BF交CD于点M,如图所示:
∴∠NBE+∠BNE=∠BED,∠MDF+∠DMF=∠BFD.
∵和分别平分和,
∴∠NBF=2∠NBE,∠MDE=2∠MDF.
∵AB∥CD,
∴∠BNE=∠MDE,∠NBF=∠DMF.
∵
∴2(∠NBE+∠BNE)-(∠MDF+∠DMF)
∴∠CDE=∠MDE=34°.
故答案为:
根据三角形外角性质可得∠NBE+∠BNE=∠BED,∠MDF+∠DMF=∠BFD.根据平行线的性质可得∠BNE=∠MDE,∠NBF=∠DMF.根据角平分线的性质得∠NBF=2∠NBE,∠MDE=2∠MDF.最后代入 ,并进行等量代换,即可得到关于∠MDE的方程,求解即可.
28.8
解:∵ 将△ABC向右平移5个单位长度得到△DEF,
∴BE=CF=5,
∵ 点B,E,C,F在同一条直线上,且EC=3,
∴BC=BE+EC=5+3=8.
故答案为:8.
根据平移的性质得BE=CF=5,进而根据BC=BE+EC计算即可.
29.45
解:如图,过作于点,
设,,
由折叠可得,,
∵四边形是正方形,
∴,
∴,
∴.
故答案为:45.
过作于,设,,
由折叠得到,,根据得到,然后求出x+y即可.
30.6a3b
解: 2a2b 3a=(2×3)(a2 a)b=6a3b,
故答案为:6a3b.
根据单项式乘单项式的规则“单项式乘以单项式,把系数与相同字母分别相乘,对于只在某一个单项式含有的字母,则连同指数作为积的一个因式”进行计算即可.
31.2023
解:将x=1,y=-1代入方程可得2a-b=-1,于是2a-b+2024=-1+2024=2023
故答案为:2023.
将解代入方程再进行整体代换可得结果.
32.9
解:由已知得m+2n=2,同时3m ·9n=3m ·32n=3m+2n=32=9
故答案为:9.
将9n化为以3为底的幂,即可运用同底数幂运算的规则进行计算.
33.1
解:∵,
∴,
解得:
∴.
故答案为:1.
根据非负数的性质得到关于x,y的方程组,解方程组求出x,y,然后根据乘方的运算法则计算即可.
34.80°;80°;100°
解:如图所示:
由图可得,∠1的同位角是∠EGB,∠1的内错角是∠AGF,∠1的同旁内角是∠BGF,
∵∠2=100°,∠2+∠EGB=180°,∠2=∠BGF.
∴∠AGF=EGB=180°-∠2=80°,∠BGF=100°.
∴ ∠1的同位角等于80°,∠1的内错角等于80°,∠1的同旁内角等于100°.
故答案为:80°;80°;100°.
根据图形分析出∠1的同位角,内错角和同旁内角,然后根据这三个角和∠2的关系分别求值即可.
35.(1)35
(2)
解:(1)∠AED'+∠DED'=180°得∠DED'=70°,由折叠可知∠DEF=∠D'EF,故∠DEF=35°,又由AD||BC得∠EFB=∠DEF=35°
故填:35°.
(2)由图(1),AD||BC得∠FED'=∠EFB=12(1800-x)=90°-12x,
而CF'||D'E得∠EFC'+∠FED'=180得∠EFC'=180°-(90°-12x)=90°+12x ,
得∠BFC'=∠EFC'-∠EFB=90°+12x-(90°-12x)=x
由折叠可知∠BFC''=∠BFC'=x,而∠EFC''=∠BFC''-∠EFB=x-(90°-12x)=32x-90°
故填:.
直接由折叠的性质得到∠DEF的度数,再由平行内错角相等可得∠EFB的度数.而(2)问中需要反复利用平行的性质与折叠的性质进行导角.
36.
解:由题意得,
故答案为:
根据提公因式法、公式法进行因式分解,进而即可求解。
37.40°
解:如图,
∵AD||BC,
∴∠1=∠DAB=70°,
由折叠的性质知∠2=∠1=70°,
∴故∠CBF=180°-∠1-∠2=180°-70°-70°=40°,
故答案为:40°.
由二直线平行,内错角相等,可得∠1的度数,由折叠的性质可得∠1=∠2,进而根据平角定义即可求得∠CBF的度数.
38.2014
解:∵是方程的一组解,
∴,
∴,
故答案为:2014.
根据二元一次方程的解的定义可得,然后对所求式子变形,整体代入计算即可.
39.
解:关于x、y的方程组 可化为,
与关于x、y的方程组为同解方程组,
根据整体换元可知
解得.
故答案为:.
整体法观察两个方程为同解方程,整体换元即可求解x、y的值.
40.-2
解:∵(x+3)(x 5)= x2 5x+3x 15=x2 2x 15,
∴m= 2.
故答案为: 2.
根据多项式与多项式的乘法法则将左式展开并合并同类项,然后根据多项式的性质可得m的值.
41.
解:由平移的性质得△ABC≌△A'B'C',
∴S△ABC=S△A'B'C',
设三角形ABC中空白面积为S上,三角形A'B'C'中空白面积为S下,
∴S上=S△ABC-S阴影,S下=S△A'B'C'-S阴影,
∴S上=S下,
∵阴影部分面积与所有空白部分面积之比为1:6,
∴设阴影部分面积为x,则所有空白部分面积为6x,
∴S上=3x,
∴S△ABC=S上+S阴影=3x+x=4x,
∴阴影部分面积与三角形ABC面积的比值为;
故答案为:.
根据平移可得△ABC与△A'B'C'的面积相等,推得上、下两个空白部分面积相等,结合已知条件即可求出阴影部分面积与三角形ABC面积的比值.
42.
解:
=.
故答案为:.
多项式÷单项式,用多项式的每一项去除单项式,并把所得的结果相加即可.
同课章节目录
