5.7第 2 课时二次函数的应用(2)(同步练习)(无答案)2024-2025学年九年级下册青岛版数学
文档属性
| 名称 | 5.7第 2 课时二次函数的应用(2)(同步练习)(无答案)2024-2025学年九年级下册青岛版数学 |  | |
| 格式 | docx | ||
| 文件大小 | 102.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 09:30:04 | ||
图片预览


文档简介
第 2 课时二次函数的应用(2)
(1)在比赛中 ,某次羽毛球的运动路线可以看作是抛物线 x2 +bx+c的一部分(见图5-7-36) ,其
中出球点 B离地面点 O的距离是 1 m ,球落地点 A到点 O的距离是 4 m ,则这条抛物线的解析式是( ) .
图 5-7-36 图 5-7-37
(2)如图 5-7-37所示 ,从地面垂直向上抛出一小球 ,小球的高度 h(m) 与小球的运动时间 t(s) 之间的函 数关系式是 h= 9.8t-4. 9t2 . 若小球的高度为 4. 9 m ,则小球的运动时间为( )秒 .
A.0. 6 B.1 C.1. 5 D.2
(3)汽车刹车距离 S(m)与速度 v(km/h)之间的函数关系是 在一辆车速为100km/h的汽车
前方80 m处 ,发现停放着一辆故障车 ,此时刹车 危险(填 “有 ”或 “没有 ”) .
(4)有一座拱桥洞呈抛物线形状 . 这个桥洞的最大高度为 16 m ,跨度为40 m. 现把它的示意图放在如图
5-7-38所示的直角坐标系中 ,则该抛物线对应的函数关系式为 .
图 5-7-38
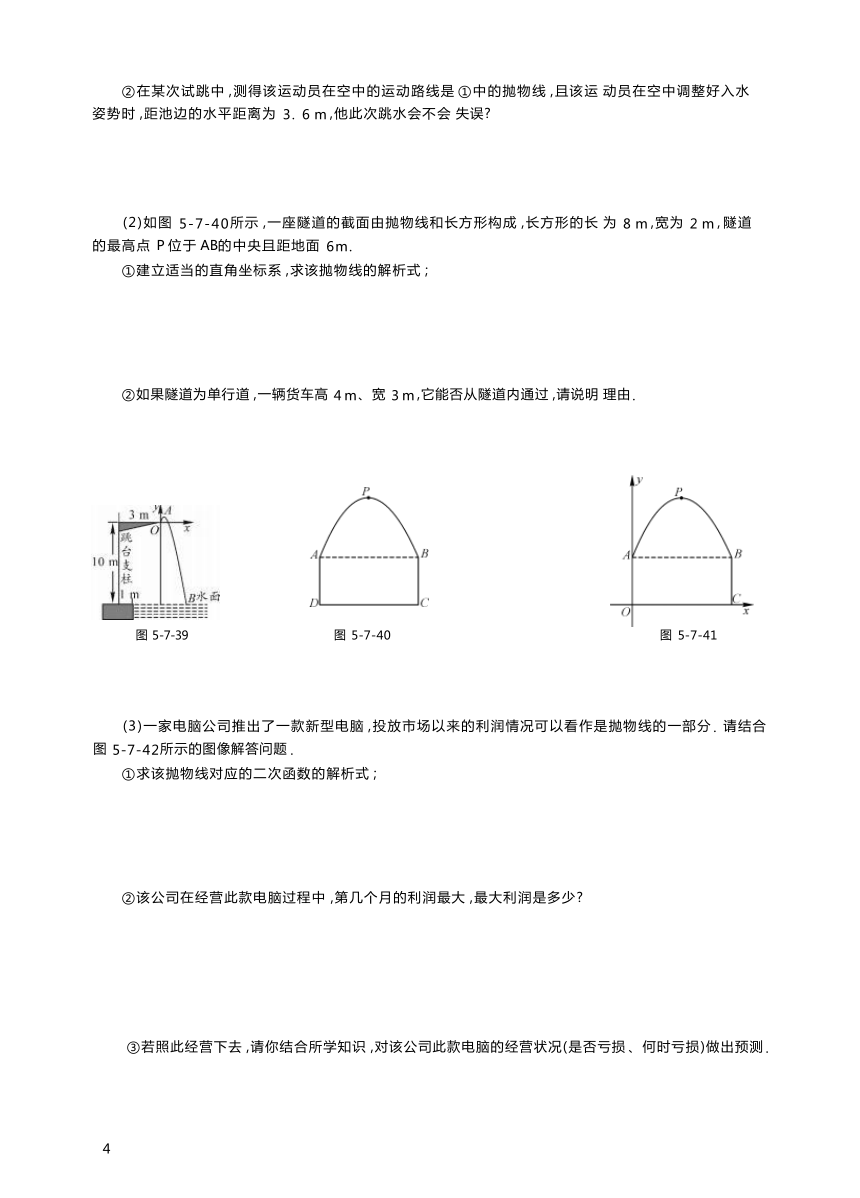
(1)某跳水运动员进行 10 m 跳台跳水训练时 ,身体(看成一点)在空中的运动路线是如图 5-7-39所示直 角坐标系下经过原点 O的一条抛物线(图中标出的数据为已知条件) . 在跳某个规定动作时 ,正常情况下 ,该
运动员在空中的最高处距水面 10 m ,入水处距池边的距离为 4 m. 运动员在距水面高度为 5 m 以前 ,必须
完成规定的翻腾动作 ,并调整好入水姿势 ,否则就会出现失误 .
①求这条抛物线的解析式 ;
1
②在某次试跳中 ,测得该运动员在空中的运动路线是 ①中的抛物线 ,且该运 动员在空中调整好入水姿势时 ,距池边的水平距离为 3. 6 m ,他此次跳水会不会 失误
(2)如图 5-7-40所示 ,一座隧道的截面由抛物线和长方形构成 ,长方形的长 为 8 m ,宽为 2 m , 隧道的最高点 P 位于 AB的中央且距地面 6m.
①建立适当的直角坐标系 ,求该抛物线的解析式 ;
②如果隧道为单行道 ,一辆货车高 4 m、宽 3 m ,它能否从隧道内通过 ,请说明 理由 .
图 5-7-39 图 5-7-40 图 5-7-41
(3)一家电脑公司推出了一款新型电脑 ,投放市场以来的利润情况可以看作是抛物线的一部分 . 请结合 图 5-7-42所示的图像解答问题 .
①求该抛物线对应的二次函数的解析式 ;
②该公司在经营此款电脑过程中 ,第几个月的利润最大 ,最大利润是多少
③若照此经营下去 ,请你结合所学知识 ,对该公司此款电脑的经营状况(是否亏损 、何时亏损)做出预测 .
图 5-7-42
基础训练
(1)心理学家发现 ,学生对概念的接受能力 y与提出概念所用的时间 x(min) 之间满足函数关系 y= -
0. 1x2 +2. 6x+43(0≤x≤30). y值越大 ,表示接受能力越强 . 如果学生的接受能力逐步增强 ,则 x 的取值范 围是( ) .
A.0≤x≤13 B.13≤x≤26 C.0≤x≤26 D.13≤x≤30
(2)图 5-7-43是某河上一座古拱桥的截面图 . 拱桥桥洞上沿是抛物线形状 . 抛物线两端点与水面的距离 都是 1 m ,拱桥的跨度为 10 m ,桥洞与水面的最大距离是 5 m ,桥洞两侧壁上各有一盏距离水面 4 m 的景观 灯 . 若把拱桥的截面图放在直角坐标系中 ,则两盏景观灯之间的水平距离是( ) .
A.3 m B.4 m
C.5 m D.6 m
(3)某飞机着陆后滑行的路程 s(m) 与时间 t(s) 之间的关系式为 s= 60t- 1. 5t2 ,试 问 飞 机 着 陆 后 滑 行 m 才能停下来 .
(4)竖直向上发射的小球的高度 h(m) 关于运动时间 t(s) 的函数 表达式为 h=t2 +t, 其 图 像 如 图 5-7-44所 示 . 若 小 球 在 发 射 后 第 2 s 与第 6 s时的高度相等 ,则小球的高度最高时是第 s.
图 5-7-43 图 5-7-44 图 5-7-45
(5)图 5-7-45是某地一座抛物线形拱桥 . 桥拱在竖直平面内 ,与水平桥面相交于 A,B两点 . 桥拱最高点 C到AB 的距离为 9 m ,AB= 36 m ,D,E为桥拱底部的两点 ,且 DE∥AB,点 E到直线 AB的距离为 7 m ,则 DE的长为 m.
拓展提高
(1)为了顺应市场要求 ,某市电子玩具制造公司技术部研制开发了一种新产品 , 年初上市后 ,公司经历 了从亏损到盈利的过程 . 图 5-7-46所示的二次函数图像(部分)展示了该公司年初以来累积利润 s(万元) 与 销售时间t(月)之间的 关 系(即 前 t个 月的 利 润 总 和 s 和 t 之 间 的 关 系) . 根 据 图 像 提 供 的 信 息 , 解 答 下 列 问题 .
①由已知图像上的三点坐标 ,求累积利润 s(万元)与时间t(月)之间的函数关系式 ;
②截止到几月末 ,公司累积利润可达到 6万元
③第 9个月该公司所获利润是多少万元
图 5-7-46
(2)如图 5-7-47所示 ,河上有一座抛物线形桥洞 , 已知桥下的水面离桥拱顶部 3 m 时 ,水面宽 AB为 6 m.
①当水位上升 0. 5 m 时 ,水面的宽度 CD为多少米
②有一艘游船 ,它的左右两边缘最宽处有一个长方体形状的遮阳棚 ,此船正对着桥洞在上述河流中航行. a. 若一艘游船宽(指船的最大宽度)为 2 m,从水面到棚顶的高度为 1. 8 m,这艘游船能否从桥洞下通过
b. 若从水面到棚顶的高度为 m 的游船刚好能从桥洞下通过 ,则这艘游船的最大宽度是多少米
图 5-7-47
(3)在一次羽毛球赛中 , 甲运动员在离地面 m 的点 P 处发球 ,球的运动轨迹 PAN 可看作一个抛物线
的一部分 . 当球运动到最高点 A时 ,其高度为 3 m ,离甲运动员站立地点 O的水平距离为 5 m ,球网 BC离点 O的水平距离为 6 m. 以点 O为原点建立如图 5-7-48所示的直角坐标系 , 乙运动员站立地点 M 的坐标为 (m,0) .
①求抛物线的解析式(不要求写出自变量的取值范围) ;
②求羽毛球落地点 N 离球网的水平距离(即 NC的长) ;
③乙运动员原地起跳后可接球的最大高度为 2. 4 m. 若乙运动员因为接球高度不够而失球 ,求 m 的取值范围.
图 5-7-48
发散思维
(1)图 5-7-49是正在修建的某隧道的横截面 . 这个横截面由一抛物线和一矩形构成 ,其行车道 CD总宽 度为 8 m , 隧道为单行线 2 车道 .
①建立恰当的直角坐标系 ,并求出隧道拱抛物线的解析式 ;
②在隧道拱的两侧距地面 3 m 高处各安装一盏路灯 ,在 ①的直角坐标系中用坐标表示出其中一盏路灯 的位置 ;
③为了保证行车安全 ,要求行驶车辆顶部(设为平顶)与隧道拱在竖直方向上高度之差至少有 0. 5 m. 现 有一辆汽车 ,装载货物后其宽度为 4 m ,车载货物的顶部与路面的距离为2. 5 m. 该车能否通过这个隧道 请
说明理由 .
图 5-7-49
(2)在足球比赛中 , 当守门员远离球门时 ,进攻队员常常使用 “吊射 ”的战术(把球高高地挑过守门员的 头顶 ,射入球门) . 一位球员在离对方球门 30 m 的 M 处起脚吊射 ,假如球飞行的路线是一条抛物线 ,在离球
门 14 m 时 ,足球达到最大高度 m. 如图 5-7-50a所示 , 以球门底部为坐标原点建立直角坐标系 ,球门 PQ
的高度为 2. 44 m.
①通过计算说明 ,球是否会进球门
②如果守门员站在距离球门 2 m 远处 ,而守门员跳起后最高能摸到 2. 75 m 处 ,他能否在空中截住这次 吊射
③如图 5-7-50b所示 ,在另一次地面进攻中 ,假如守门员站在离球门中央 2 m 远的 A点处防守 ,进攻队 员在离球门中央 12 m 的 B处以 120 km/h的球速起脚射门 ,射向球门的立柱 C. 球门的宽度 CD 为 7. 2 m , 而守门员防守的最远水平距离 S和时间 t之间的函数关系式为S= 10t,这次守门员能否挡住球
a b
图 5-7-50
4
(1)在比赛中 ,某次羽毛球的运动路线可以看作是抛物线 x2 +bx+c的一部分(见图5-7-36) ,其
中出球点 B离地面点 O的距离是 1 m ,球落地点 A到点 O的距离是 4 m ,则这条抛物线的解析式是( ) .
图 5-7-36 图 5-7-37
(2)如图 5-7-37所示 ,从地面垂直向上抛出一小球 ,小球的高度 h(m) 与小球的运动时间 t(s) 之间的函 数关系式是 h= 9.8t-4. 9t2 . 若小球的高度为 4. 9 m ,则小球的运动时间为( )秒 .
A.0. 6 B.1 C.1. 5 D.2
(3)汽车刹车距离 S(m)与速度 v(km/h)之间的函数关系是 在一辆车速为100km/h的汽车
前方80 m处 ,发现停放着一辆故障车 ,此时刹车 危险(填 “有 ”或 “没有 ”) .
(4)有一座拱桥洞呈抛物线形状 . 这个桥洞的最大高度为 16 m ,跨度为40 m. 现把它的示意图放在如图
5-7-38所示的直角坐标系中 ,则该抛物线对应的函数关系式为 .
图 5-7-38
(1)某跳水运动员进行 10 m 跳台跳水训练时 ,身体(看成一点)在空中的运动路线是如图 5-7-39所示直 角坐标系下经过原点 O的一条抛物线(图中标出的数据为已知条件) . 在跳某个规定动作时 ,正常情况下 ,该
运动员在空中的最高处距水面 10 m ,入水处距池边的距离为 4 m. 运动员在距水面高度为 5 m 以前 ,必须
完成规定的翻腾动作 ,并调整好入水姿势 ,否则就会出现失误 .
①求这条抛物线的解析式 ;
1
②在某次试跳中 ,测得该运动员在空中的运动路线是 ①中的抛物线 ,且该运 动员在空中调整好入水姿势时 ,距池边的水平距离为 3. 6 m ,他此次跳水会不会 失误
(2)如图 5-7-40所示 ,一座隧道的截面由抛物线和长方形构成 ,长方形的长 为 8 m ,宽为 2 m , 隧道的最高点 P 位于 AB的中央且距地面 6m.
①建立适当的直角坐标系 ,求该抛物线的解析式 ;
②如果隧道为单行道 ,一辆货车高 4 m、宽 3 m ,它能否从隧道内通过 ,请说明 理由 .
图 5-7-39 图 5-7-40 图 5-7-41
(3)一家电脑公司推出了一款新型电脑 ,投放市场以来的利润情况可以看作是抛物线的一部分 . 请结合 图 5-7-42所示的图像解答问题 .
①求该抛物线对应的二次函数的解析式 ;
②该公司在经营此款电脑过程中 ,第几个月的利润最大 ,最大利润是多少
③若照此经营下去 ,请你结合所学知识 ,对该公司此款电脑的经营状况(是否亏损 、何时亏损)做出预测 .
图 5-7-42
基础训练
(1)心理学家发现 ,学生对概念的接受能力 y与提出概念所用的时间 x(min) 之间满足函数关系 y= -
0. 1x2 +2. 6x+43(0≤x≤30). y值越大 ,表示接受能力越强 . 如果学生的接受能力逐步增强 ,则 x 的取值范 围是( ) .
A.0≤x≤13 B.13≤x≤26 C.0≤x≤26 D.13≤x≤30
(2)图 5-7-43是某河上一座古拱桥的截面图 . 拱桥桥洞上沿是抛物线形状 . 抛物线两端点与水面的距离 都是 1 m ,拱桥的跨度为 10 m ,桥洞与水面的最大距离是 5 m ,桥洞两侧壁上各有一盏距离水面 4 m 的景观 灯 . 若把拱桥的截面图放在直角坐标系中 ,则两盏景观灯之间的水平距离是( ) .
A.3 m B.4 m
C.5 m D.6 m
(3)某飞机着陆后滑行的路程 s(m) 与时间 t(s) 之间的关系式为 s= 60t- 1. 5t2 ,试 问 飞 机 着 陆 后 滑 行 m 才能停下来 .
(4)竖直向上发射的小球的高度 h(m) 关于运动时间 t(s) 的函数 表达式为 h=t2 +t, 其 图 像 如 图 5-7-44所 示 . 若 小 球 在 发 射 后 第 2 s 与第 6 s时的高度相等 ,则小球的高度最高时是第 s.
图 5-7-43 图 5-7-44 图 5-7-45
(5)图 5-7-45是某地一座抛物线形拱桥 . 桥拱在竖直平面内 ,与水平桥面相交于 A,B两点 . 桥拱最高点 C到AB 的距离为 9 m ,AB= 36 m ,D,E为桥拱底部的两点 ,且 DE∥AB,点 E到直线 AB的距离为 7 m ,则 DE的长为 m.
拓展提高
(1)为了顺应市场要求 ,某市电子玩具制造公司技术部研制开发了一种新产品 , 年初上市后 ,公司经历 了从亏损到盈利的过程 . 图 5-7-46所示的二次函数图像(部分)展示了该公司年初以来累积利润 s(万元) 与 销售时间t(月)之间的 关 系(即 前 t个 月的 利 润 总 和 s 和 t 之 间 的 关 系) . 根 据 图 像 提 供 的 信 息 , 解 答 下 列 问题 .
①由已知图像上的三点坐标 ,求累积利润 s(万元)与时间t(月)之间的函数关系式 ;
②截止到几月末 ,公司累积利润可达到 6万元
③第 9个月该公司所获利润是多少万元
图 5-7-46
(2)如图 5-7-47所示 ,河上有一座抛物线形桥洞 , 已知桥下的水面离桥拱顶部 3 m 时 ,水面宽 AB为 6 m.
①当水位上升 0. 5 m 时 ,水面的宽度 CD为多少米
②有一艘游船 ,它的左右两边缘最宽处有一个长方体形状的遮阳棚 ,此船正对着桥洞在上述河流中航行. a. 若一艘游船宽(指船的最大宽度)为 2 m,从水面到棚顶的高度为 1. 8 m,这艘游船能否从桥洞下通过
b. 若从水面到棚顶的高度为 m 的游船刚好能从桥洞下通过 ,则这艘游船的最大宽度是多少米
图 5-7-47
(3)在一次羽毛球赛中 , 甲运动员在离地面 m 的点 P 处发球 ,球的运动轨迹 PAN 可看作一个抛物线
的一部分 . 当球运动到最高点 A时 ,其高度为 3 m ,离甲运动员站立地点 O的水平距离为 5 m ,球网 BC离点 O的水平距离为 6 m. 以点 O为原点建立如图 5-7-48所示的直角坐标系 , 乙运动员站立地点 M 的坐标为 (m,0) .
①求抛物线的解析式(不要求写出自变量的取值范围) ;
②求羽毛球落地点 N 离球网的水平距离(即 NC的长) ;
③乙运动员原地起跳后可接球的最大高度为 2. 4 m. 若乙运动员因为接球高度不够而失球 ,求 m 的取值范围.
图 5-7-48
发散思维
(1)图 5-7-49是正在修建的某隧道的横截面 . 这个横截面由一抛物线和一矩形构成 ,其行车道 CD总宽 度为 8 m , 隧道为单行线 2 车道 .
①建立恰当的直角坐标系 ,并求出隧道拱抛物线的解析式 ;
②在隧道拱的两侧距地面 3 m 高处各安装一盏路灯 ,在 ①的直角坐标系中用坐标表示出其中一盏路灯 的位置 ;
③为了保证行车安全 ,要求行驶车辆顶部(设为平顶)与隧道拱在竖直方向上高度之差至少有 0. 5 m. 现 有一辆汽车 ,装载货物后其宽度为 4 m ,车载货物的顶部与路面的距离为2. 5 m. 该车能否通过这个隧道 请
说明理由 .
图 5-7-49
(2)在足球比赛中 , 当守门员远离球门时 ,进攻队员常常使用 “吊射 ”的战术(把球高高地挑过守门员的 头顶 ,射入球门) . 一位球员在离对方球门 30 m 的 M 处起脚吊射 ,假如球飞行的路线是一条抛物线 ,在离球
门 14 m 时 ,足球达到最大高度 m. 如图 5-7-50a所示 , 以球门底部为坐标原点建立直角坐标系 ,球门 PQ
的高度为 2. 44 m.
①通过计算说明 ,球是否会进球门
②如果守门员站在距离球门 2 m 远处 ,而守门员跳起后最高能摸到 2. 75 m 处 ,他能否在空中截住这次 吊射
③如图 5-7-50b所示 ,在另一次地面进攻中 ,假如守门员站在离球门中央 2 m 远的 A点处防守 ,进攻队 员在离球门中央 12 m 的 B处以 120 km/h的球速起脚射门 ,射向球门的立柱 C. 球门的宽度 CD 为 7. 2 m , 而守门员防守的最远水平距离 S和时间 t之间的函数关系式为S= 10t,这次守门员能否挡住球
a b
图 5-7-50
4
