第四单元正比例与反比例(提升卷)(含解析)-2024-2025学年六年级数学下册常考易错题(北师大版)
文档属性
| 名称 | 第四单元正比例与反比例(提升卷)(含解析)-2024-2025学年六年级数学下册常考易错题(北师大版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 08:10:37 | ||
图片预览


文档简介
/ 让教学更有效 精品试卷 | 数学学科
第四单元正比例与反比例(提升卷)
2024-2025学年六年级数学下册常考易错题(北师大版)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.淘气和爸爸的年龄变化情况如下表,下面描述错误的是( )。
淘气的年龄/岁 6 7 8 9
爸爸的年龄/岁 32 33 34 35
A.淘气和爸爸的年龄都在增加
B.淘气和爸爸的年龄差不变
C.淘气的年龄和爸爸的年龄成正比例关系
2.一列火车,4小时行320千米。照这样的速度,从甲城到乙城有420千米,( )小时可以到达?如果火车速度提高5%,( )小时就可以到达。( )
A.2.25;2 B.8.25;8 C.5.25;5 D.6.25;4
3.松树村的特菜生产基地,5天平整土地1.2公顷。照这样的效率,再工作2天,一共可以平整土地( )。
A.0.48公顷 B.8.16公顷 C.1.68公顷 D.16.8公顷
4.松树村特菜生产基地,计划平整1.68公顷土地,5天平整了1.2公顷。照这样的效率,剩下的任务还要( )天完成。
A.2 B.1 C.4 D.3
5.自然数和它的倒数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
二、填空题
6.判断下面的两个量成不成比例,如果成分别成什么比例,写在括号里。
打疫苗时,每小时打疫苗的人数一定,打疫苗的总人数与所用时间( )。
7.自行车前齿轮有48齿,后齿轮有16齿。当前齿轮转5圈时,后齿轮转( )圈。
8.在一定时间范围内,人的体重会随着年龄的增长而( )。
9.a÷b=c(a,b,c均不为0),当c一定时,a和b成( );当a一定时,b和c成( );当b一定时,a和c成( )。
10.把300mL的水倒入底面积不同的杯子中。
底面积/cm2 10 15 20 30 60
高度/cm 30 20 15 10 5
体积/cm3 300 300 300 300 300
从表中可以看出:( )随着( )的增加而( ),( )随着( )的减少而( )。
11.淘气今年12岁,张老师今年28岁。当淘气28岁时,张老师( )岁;当张老师60岁退休的时候,淘气( )岁。用字母m表示淘气的年龄,n表示张老师的年龄,m和n两个量之间的关系可以用式子( )表示。
12.一辆汽车油箱里储油102升,行驶了56千米正好耗油8升。照这样计算,剩下的油还可以行驶( )千米。
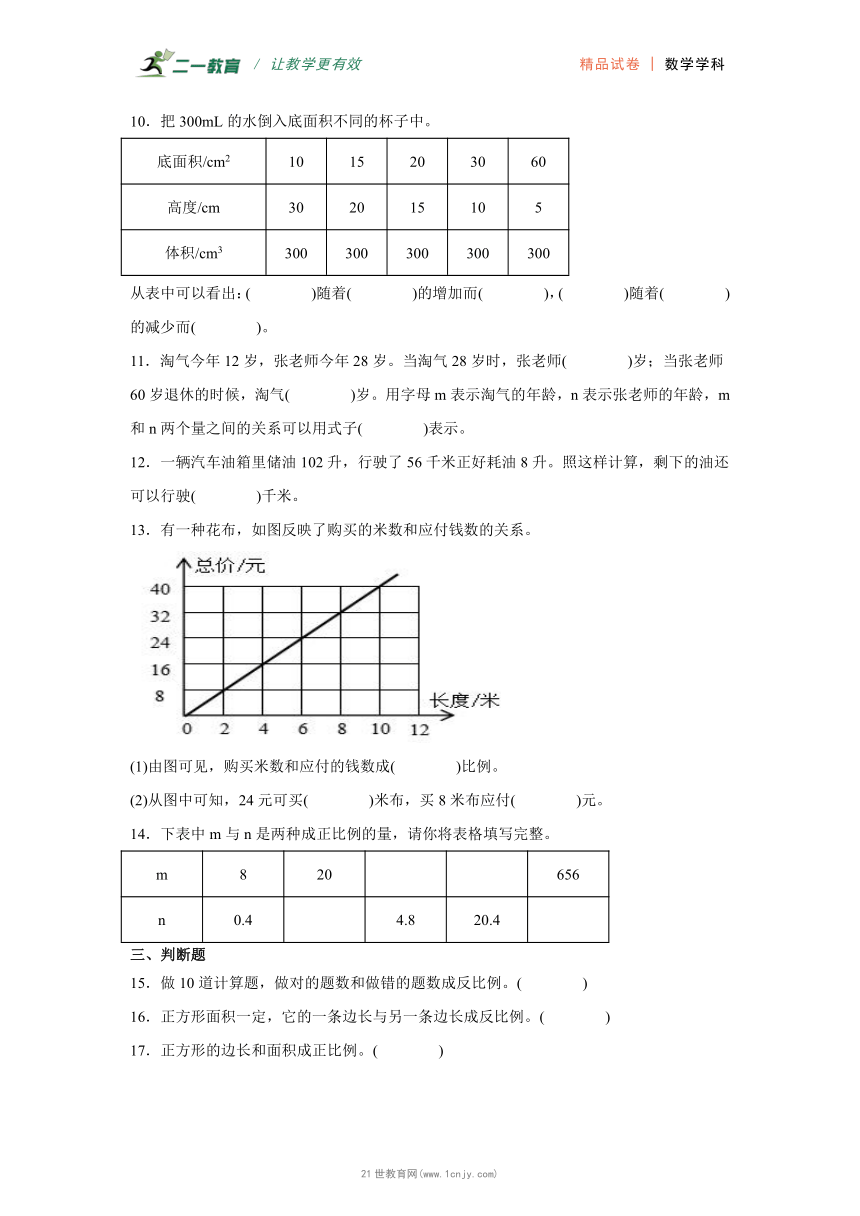
13.有一种花布,如图反映了购买的米数和应付钱数的关系。
(1)由图可见,购买米数和应付的钱数成( )比例。
(2)从图中可知,24元可买( )米布,买8米布应付( )元。
14.下表中m与n是两种成正比例的量,请你将表格填写完整。
m 8 20 656
n 0.4 4.8 20.4
三、判断题
15.做10道计算题,做对的题数和做错的题数成反比例。( )
16.正方形面积一定,它的一条边长与另一条边长成反比例。( )
17.正方形的边长和面积成正比例。( )
四、作图题
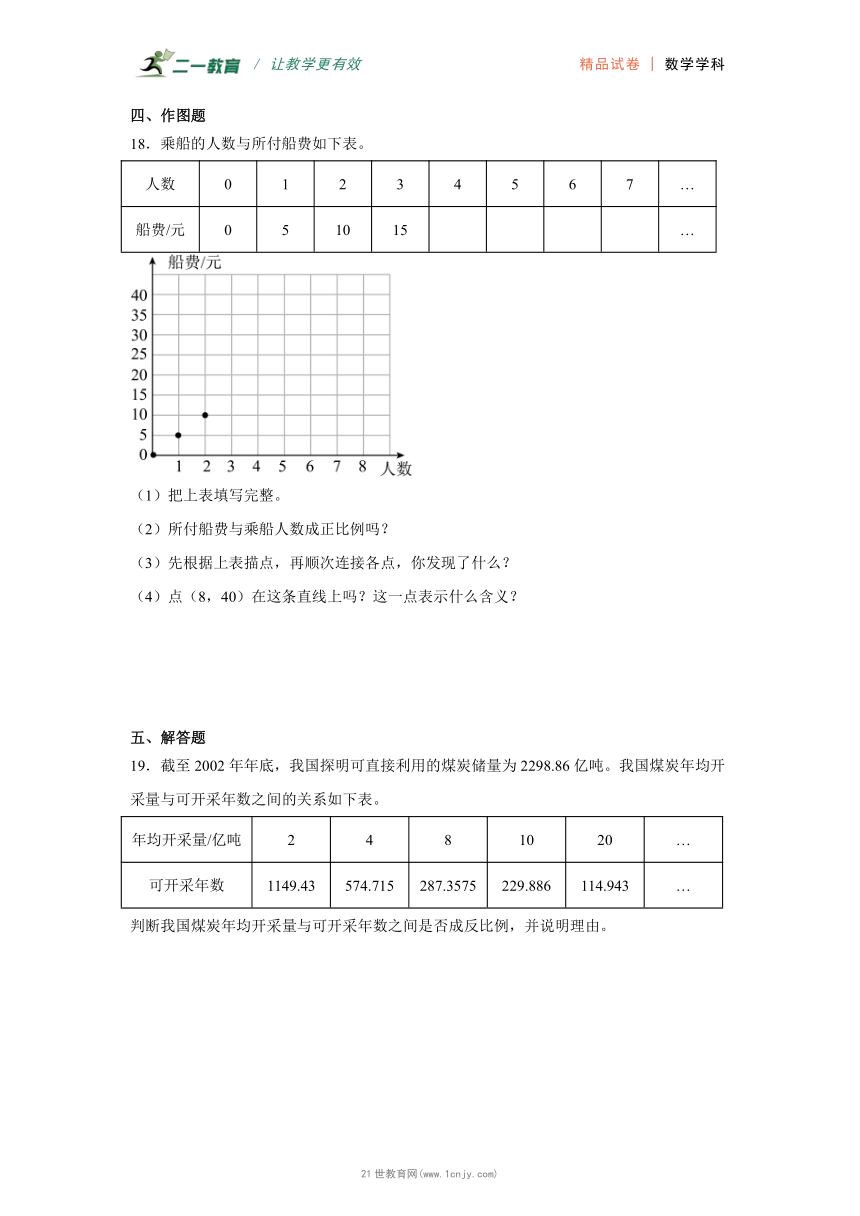
18.乘船的人数与所付船费如下表。
人数 0 1 2 3 4 5 6 7 …
船费/元 0 5 10 15 …
(1)把上表填写完整。
(2)所付船费与乘船人数成正比例吗?
(3)先根据上表描点,再顺次连接各点,你发现了什么?
(4)点(8,40)在这条直线上吗?这一点表示什么含义?
五、解答题
19.截至2002年年底,我国探明可直接利用的煤炭储量为2298.86亿吨。我国煤炭年均开采量与可开采年数之间的关系如下表。21*cnjy*com
年均开采量/亿吨 2 4 8 10 20 …
可开采年数 1149.43 574.715 287.3575 229.886 114.943 …
判断我国煤炭年均开采量与可开采年数之间是否成反比例,并说明理由。
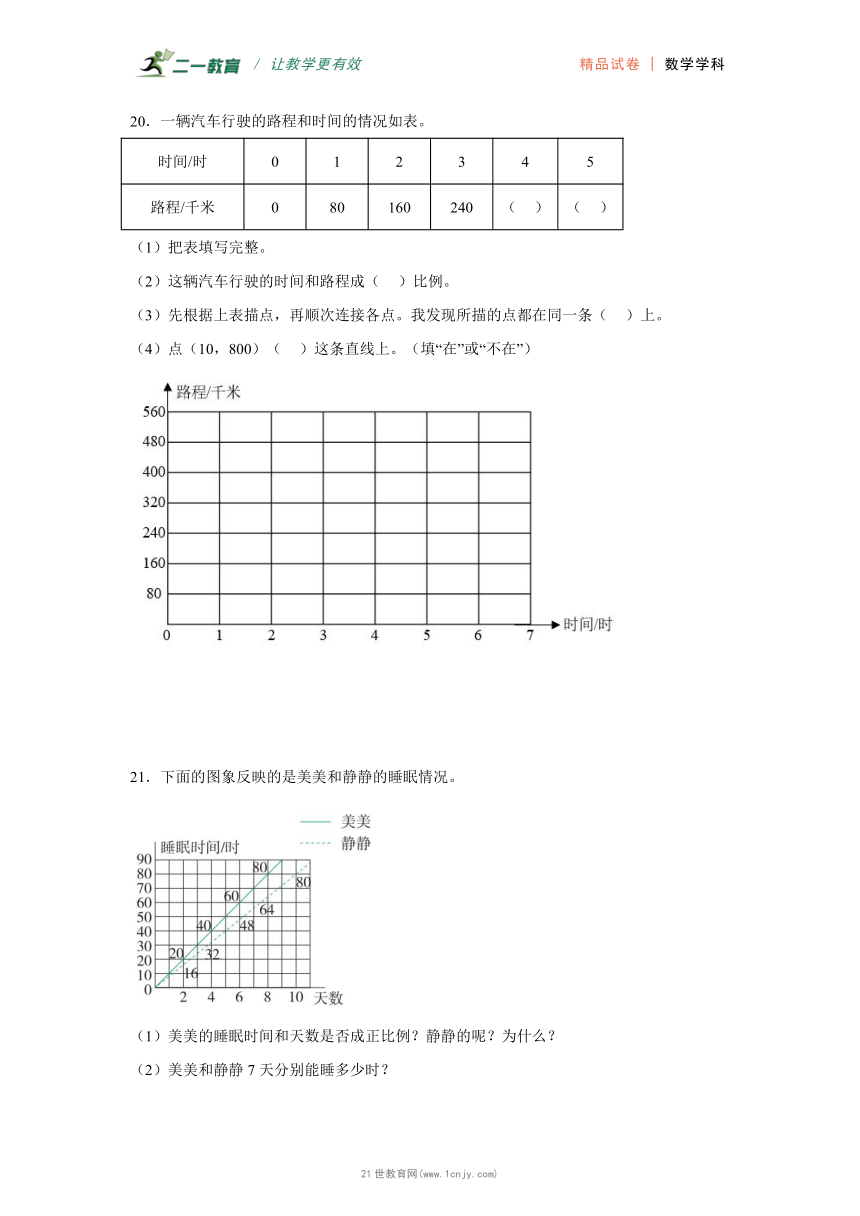
20.一辆汽车行驶的路程和时间的情况如表。
时间/时 0 1 2 3 4 5
路程/千米 0 80 160 240 ( ) ( )
(1)把表填写完整。
(2)这辆汽车行驶的时间和路程成( )比例。
(3)先根据上表描点,再顺次连接各点。我发现所描的点都在同一条( )上。
(4)点(10,800)( )这条直线上。(填“在”或“不在”)
21.下面的图象反映的是美美和静静的睡眠情况。
(1)美美的睡眠时间和天数是否成正比例?静静的呢?为什么?
(2)美美和静静7天分别能睡多少时?
22.水是生命之源。向阳小学对同学们进行了节约用水教育。苗苗测试了一个打开的水龙头的流水量,测试结果如下表所示。2·1·c·n·j·y
时间/秒 0 10 20 30 40
出水量/L 0 2 4 6 8
(1)表中的时间和出水量是否成正比例,为什么?
(2)先根据上表中的数据描点,再顺次连接各点。
(3)看图估计,这个水龙头45秒的出水量是多少?
23.书籍是人类进步的阶梯,让课外书为孩子们打开一扇扇窗,开启一道道门。文明小学在五月中旬开展了“携手经典,浸润和美”的读书节活动。六(1)班的三名同学同读一本书,下表记录了每人每天看的页数和所需时间。www.21-cn-jy.com
(1)把表格补充完整。
李欢 孙林 董芊宜
每天看的页数 15 20 30
看完所需时间/天 8
(2)三名同学看书的过程中哪个量没变?每天看的页数和看完所需的天数有什么关系?
(3)看了3天后,他们已看的页数和剩下的页数成反比例吗?为什么?
24.一辆汽车的行驶路程和耗油量如下表。
路程/千米 10 20 30 40 50 …
耗油量/升 1.2 2.4 3.6 4.8 6.0 …
(1)观察上表,汽车的行驶路程和耗油量成( )比例。
(2)上图是这辆汽车出发时和到达时的油表,这辆汽车大约行驶了多少千米?(用比例解)
25.购买一种丝带的长度和应付金额如下表。
长度 0 1 2 3 4 5 …
应付金额元 0 4 8 12 16 20 …
(1)判断应付金额与长度是否成正比例关系,说明理由。
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接。
(3)购买7.5米丝带需要( )元;76元最多可以购买( )长的丝带。
26.看电影的人数与所付票费如下表。
人数 0 1 2 3 4 5 6 7 8 …
票费/元 0 2 4 6 …
(1)通过自己画图并连接各点,你发现了什么?
(2)利用自己画的图,把下表填完整。
人数 16 25
票费/元 36 56 60 66
27.生产240个零件,工作效率和工作时间如下表。
工作效率(个/时) 120 80 60 48 40 …
工作时间/时 2 3 4 …
(1)填写上表,工作时间是随着哪个量的变化而变化的?
(2)相对应的两个数的乘积各是多少?
(3)这个乘积的实际意义是什么?你能用式子表示出它与工作效率、工作时间之间的关系吗?
(4)工作效率和工作时间成反比例吗?为什么?
《第四单元正比例与反比例(提升卷)-2024-2025学年六年级数学下册常考易错题(北师大版)》参考答案21·世纪*教育网
1.C
【分析】淘气和爸爸的年龄每年都增加1岁,但年龄差不变;如果相对应的两个量x和y的比值一定,那么这两个量的关系成正比例关系,二人年龄的比值可以通过计算来得出结果,明显不是固定的。21*cnjy*com
【详解】A.从表中数据可以看出,淘气和爸爸的年龄都在增加,说法正确。
B.32-6=33-7=34-8=35-9=26(岁)
二人的年龄差为26岁,说法正确。
C.6∶32==
7∶33=
8∶34==
9∶35=
比值不相等,所以淘气和爸爸的年龄不成正比例,说法错误。
故答案为:C
【点睛】本题考查了正比例的意义的理解和灵活应用,同时考查了学生分析解决问题的能力。
2.C
【分析】根据题意可知,路程÷时间=速度(一定),则路程和时间的比值一定,它们成正比例关系,据此设从甲城到乙城有420千米,x小时可以到达,列比例为420∶x=320∶4,然后解出比例即可;先用320÷4求出火车的速度,如果火车速度提高5%,则把原来火车的速度看作单位“1”,现在火车的速度是原来的(1+5%),根据百分数乘法的意义,用原来的速度乘(1+5%)即可求出现在的速度,然后用420千米除以现在火车的速度,即可求出如果火车速度提高5%,几小时就可以到达。21教育名师原创作品
【详解】解:设从甲城到乙城有420千米,x小时可以到达。
420∶x=320∶4
320x=420×4
320x=1680
x=1680÷320
x=5.25
320÷4=80(千米/小时)
80×(1+5%)
=80×1.05
=84(千米/小时)
420÷84=5(小时)
从甲城到乙城有420千米,5.25小时可以到达;如果火车速度提高5%,5小时就可以到达。
故答案为:C
【点睛】本题主要考查了正比例的应用,掌握速度、时间、路程三者之间的关系是解答本题的关键。
3.C
【分析】根据题意可知,平整土地的总公顷数÷天数=每天平整土地的公顷数(一定),平整土地的总公顷数和天数的比值一定,它们成正比例;据此设2天可以平整土地x公顷,列比例为:x∶2=1.2∶5,然后解出比例即可。21·cn·jy·com
【详解】解:设2天可以平整土地x公顷。
x∶2=1.2∶5
5x=1.2×2
5x=2.4
x=2.4÷5
x=0.48
0.48+1.2=1.68(公顷)
照这样的效率,再工作2天,一共可以平整土地1.68公顷。
故答案为:C
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
4.A
【分析】根据题意可知,平整土地的总公顷数÷天数=每天平整土地的公顷数(一定),则平整土地的总公顷数和天数的比值一定,它们成正比例关系,据此设剩下的任务还要x天完成,列比例为(1.68-1.2)∶x=1.2∶5,然后解出比例即可。【来源:21cnj*y.co*m】
【详解】解:设剩下的任务还要x天完成。
(1.68-1.2)∶x=1.2∶5
0.48∶x=1.2∶5
1.2x=0.48×5
1.2x=2.4
x=2.4÷1.2
x=2
剩下的任务还要2天完成。
故答案为:A
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
5.B
【分析】根据倒数的意义(乘积是1的两个数互为倒数),由此可知:任何一个自然数(0除外)和它的倒数的乘积都是1,即这两个数的乘积一定,据此进行判断。
【详解】因为0没有倒数,所以这个自然数m不包括0,又因为:自然数m×它的倒数=1(一定),即对应的乘积一定,所以这个自然数m与它的倒数成反比例。
故答案为:B
【点睛】解答此题的关键是明白:两个量的积或者商一定,就说这两个量成反比例或正比例。
6.成正比例
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系。据此解答。
【详解】打疫苗的总人数÷所用的时间=每小时打疫苗的人数(一定),因此打疫苗的总人数与所用时间成正比例。
【点睛】两种相关联的量,若其比值一定,两种量成正比例关系。
7.15
【分析】
根据自行车中前齿轮齿数×前齿轮的转数=后齿轮齿数×后齿轮的转数,设后齿轮转x圈,列出方程,求出方程的解即可。
【详解】设后齿轮转x圈。
16x=48×5
16x=240
x=240÷16
x=15
则后齿轮转15圈。
8.增加
【详解】如:
下表是小红6岁前的体重变化情况。
年龄 出生时 2岁 4岁 6岁
体重/千克 3.5 14.0 18.0 21.0
根据表格中的数据,发现小红6岁前的体重随年龄的增长而增加。
体重是随年龄的增长而增加的,所以它们是两个相关联的量
本题属于根据正比例的意义,判断两种相关联的成不成正比例,就看这两种量是否是一个量变化,另一个量也随着变化,并且变化方向相同;且这两种量是否是对应的比值一定,再做判断。本题中一个量变化,另一个量也随着变化,但是两种量对应的比值不是一定的,因此不是正比例。21教育网
由此可得:在一定时间范围内,人的体重会随着年龄的增长而增加。
9. 正比例 反比例 正比例
【分析】
两个相关联的量,一个量随着另外一个量的变化而变化,如果两个量的商是一个定值,则说明这两个量成正比例关系;如果两个量的乘积一定,则说明这两个量成反比例关系。
【详解】
a÷b=c,当c一定时,就是商一定,则a和b成正比例;
a÷b=c,即bc=a, 当a一定时,就是乘积一定,则b和c成反比例;
a÷b=c,即a÷c=b, 当b一定时,就是一定,则a和c成反比例;
10. 高度 底面积 减少 底面积 高度 增加
【分析】从统计表中可知:两个相关联的量,底面积和高成反比例关系。一个量增加,一个量就减少,两个量的积不变。据此解答。
【详解】(高度)随着(底面积)的增加而(减少),(底面积)随着(高度)的减少而(增加)。
【点睛】熟练掌握判断两个相关联的量之间成什么比例是解答的关键。
11. 44 44 n=16+m
【分析】张老师今年的年龄-淘气今年的年龄=两人年龄差,年龄差永不变,淘气年龄+年龄差=张老师年龄;张老师年龄-年龄差=淘气年龄;据此用字母表示出两年年龄之间的关系。
【详解】28-12=16(岁)
28+16=44(岁)
60-16=44(岁)
n=16+m(答案不唯一)
当淘气28岁时,张老师44岁;当张老师60岁退休的时候,淘气44岁。用字母m表示淘气的年龄,n表示张老师的年龄,m和n两个量之间的关系可以用式子n=16+m表示。
12.658
【分析】根据题意可知,汽车的行驶路程÷耗油量=每升行驶的路程(一定),则汽车的行驶路程和耗油量的比值一定,它们成正比例关系;设剩下的油还可以行驶x千米,列比例为x∶(102-8)=56∶8,然后解出比例即可。
【详解】解:设剩下的油还可以行驶x千米。
x∶(102-8)=56∶8
x∶94=56∶8
8x=56×94
8x=5264
x=5264÷8
x=658
剩下的油还可以行驶658千米。
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
13.(1)正
(2) 6 32
【分析】(1)直接观察图像可以看出购买米数和应付的钱数成正比例关系。
(2)根据图像,直接找出24元对应的米数即可;直接找出买8米布对应的钱数,据此解答。
【详解】(1)由图可见,购买米数和应付的钱数成正比例关系。
(2)从图中可知,24元可买6米布,买8米布应付32元。
【点睛】此题考查了正比例的应用,明确两个变化的量,如果比值一定则成正比例关系。
14.96;408;
1;32.8
【分析】
x÷y=k(一定),x和y成正比例关系,m与n是两种成正比例的量,说明m与n的商一定,通过第一组数据,先求出m与n的商,根据被除数÷商=除数,商×除数=被除数,分别计算出未知的量,填表即可。21cnjy.com
【详解】8÷0.4=20
20÷20=1、20×4.8=96、20×20.4=408、656÷20=32.8
m 8 20 96 408 656
n 0.4 1 4.8 20.4 32.8
15.×
【分析】两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】做10道计算题,做对的题数+做错的题数=10,和一定,则做对的题数和做错的题数不成比例。原题说法错误。21世纪教育网版权所有
故答案为:×
【点睛】掌握反比例的意义是解题的关键。
16.×
【分析】判断两个相关联的量成什么比例关系,关键是看它们的积一定还是比值一定。如果它们的积一定,则成反比例关系;如果它们的比值一定,则成正比例关系。题干中正方形的边长相等,所以不存在两个相关联的量,据此解答。
【详解】正方形的面积公式是:,面积一定,边长就一定,不存在两个相关联的量,不构成反比例关系。
故答案为:×
【点睛】熟练掌握反比例的概念以及正方形的特征是解答本题的关键。
17.×
【分析】两个相关联的量,当比值一定时,成正比例关系,据此解答。
【详解】正方形面积=边长×边长;边长= ,比值不一定,所以正方形边长和面积不成正比例。
原题干说法错误。
故答案为:×
【点睛】明确正比例的意义是解答本题的关键。
18.(1)见详解
(2)成正比例
(3)描点见详解:发现这些点在同一条直线上,表示这两种量成正比例关系
(4)在;当人数是8人时,船费是40元
【分析】(1)根据表格中的数据,船费与乘船人数之间的关系是每增加1人,船费增加5元。据此补充表格;
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量,它们的关系叫做正比例关系。据此判断;
(3)根据表格中的数据描点、连线,结合连接后的图像写出发现;
(4)根据(3)的直线进行判断,看点(8,40)是否在直线上,如果在直线上,这点表示当人数是8人时,船费是40元。www-2-1-cnjy-com
【详解】(1)
人数 0 1 2 3 4 5 6 7 …
船费/元 0 5 10 15 20 25 30 35 …
(2)5∶1=10∶2=15∶3=20∶4=25∶5…=5(一定),即船费∶人数=单价(一定),比值一定,所以所付船费与乘船人数成正比例;
(3)如图:
发现:这些点在同一条直线上,表示这两种量成正比例关系;
(4)点(8,40)在这条直线上,表示当人数是8人时,船费是40元。
19.成反比例;理由见详解
【分析】反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量成反比例关系。
【详解】2×1149.43=4×574.715=8×287.3575=10×229.886=20×114.943…=2298.86(一定)
答:我国煤炭年均开采量与可开采年数成反比例,因为我国煤炭年均开采量×可开采年数=总煤炭储量(一定),乘积一定,则我国煤炭年均开采量与可开采年数成反比例。
20.(1)320;400
(2)正
(3)直线
(4)在
【分析】(1)根据前几组数据分别计算出这辆汽车4小时和5小时行驶的路程,填入表中;
(2)根据时间与路程的比值一定,确定行驶的时间和路程成正比例;
(3)成正比例关系的图形是一条直线,所以各点都在这条直线上;
(4)求出10与800的比值,即可确定这个点在这条直线上。
【详解】(1)根据前几组数据可知,路程∶时间=80∶1,即这辆汽车1小时行驶80千米。
4×80=320(千米)
5×80=400(千米)
所以这辆汽车4小时行驶的路程是320千米、5小时行驶的路程是400千米。
(2)1∶80=
2∶160==
3∶240==
比值一定,这辆汽车行驶的时间和路程成正比例。
(3)汽车行驶的时间和路程成正比例关系,成正比例关系的图形是一条直线,所以各点都在同一条直线上。
(4)10∶800==,所以点(10,800)在这条直线上。
【点睛】比值一定的两个量是成正比例关系的量,对应的各点都在同一条直线上。
21.(1)见详解;
(2)70小时,56小时。
【分析】(1)两个相关联的量,一个量随着另外一个量的变化而变化,且两个量的商是一个定值,则说明这两个量成正比例关系。美美的睡眠时间是随着天数的变化而变化的。将图形中美美的睡眠时间和天数相除。20÷2=10、40÷4=10、60÷6=10、80÷8=10,发现睡眠时间和天数的商是一定的。则美美的睡眠时间和天数成正比例。同理,静静的睡眠时间和天数相除。16÷2=8、32÷4=8、48÷6=8、64÷8=8、80÷10=8。则静静的睡眠时间和天数成正比例。
(2)通过(1)问中可以得出美美睡眠时间和天数的比值是10,则7天的睡眠时间=10×天数。静静睡眠时间和天数的比值是8,则7天的睡眠时间=8×天数。
【详解】(1)美美的睡眠时间和天数成正比例,因为睡眠时间÷天数=10(一定);
静静的睡眠时间和天数成正比例,因为睡眠时间÷天数=8(一定)。
(2)美美:20÷2=10(小时) 10×7=70(小时)
静静:16÷2=8(小时) 8×7=56(小时)
答:美美睡70小时,静静睡56小时。
22.(1)成正比例;理由见详解;
(2)见详解
(3)9L
【分析】(1)根据表格判断出,出水量和时间的比值一定,所以表中的时间和出水量成正比例;
(2)根据表格的数据,描出对应的点,连线即可;
(3)根据图象可知,当时间为45秒时,出水量超过8L,但没有达到10L,所以估计出水量为9L。
【详解】(1)表中的出水量和时间成正比例。
理由:(一定),也就是出水量和时间的比值一定,所以出水量和时间成正比例。
(2)如图:
(3)看图估计,这个水龙头45秒的出水量是9L。
23.(1)6;4
(2)总页数;反比例关系
(3)不成;见详解
【分析】(1)三人看的是同一本书。将李欢每天看的页数乘8天,求出书的总页数。将书总页数除以孙林每天看的页数,求出看完需要多少天。同理求出,董芊宜看完这本书需要多少天;
(2)看书过程中,书的总页数不变。乘积一定的两个量成反比例关系;
(3)乘积一定的两个量成反比例关系,据此分析解题。
【详解】(1)15×8=120(页)
120÷20=6(天)
120÷30=4(天)
填表如下:
李欢 孙林 董芊宜
每天看的页数 15 20 30
看完所需时间/天 8 6 4
(2)每天看的页数×看完需要的天数=书的总页数(一定)
答:三名同学看书的过程中,书的总页数不变。每天看的页数和看完所需的天数成反比例关系。
(3)答:看了3天后,他们已看的页数和剩下的页数不成反比例。因为已看的页数+剩下的页数=书总页数(一定),和是一定的,但积不一定。
24.(1)正;(2)125千米
【分析】(1)根据题意可知,汽车的行驶路程÷耗油量=每升行驶的路程(一定),则汽车的行驶路程和耗油量的比值一定,它们成正比例关系;
(2)根据题意可知,从出发到到达时,一共消耗了(40-25)升油,设这辆汽车大约行驶了x千米,列比例为x∶(40-25)=10∶1.2,然后解出比例即可。
【详解】(1)10÷1.2=(千米/升)
20÷2.4=(千米/升)
30÷3.6=(千米/升)
……
汽车的行驶路程和耗油量的比值一定,它们成正比例关系;
(2)解:设这辆汽车大约行驶了x千米。
x∶(40-25)=10∶1.2
x∶15=10∶1.2
1.2x=15×10
1.2x=150
x=150÷1.2
x=125
答:这辆汽车大约行驶了125千米。
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
25.(1)见详解
(2)见详解
(3)30;19
【分析】(1)如果两个相关联的量的比值一定,那么这两个相关联的量成正比例关系,据此解答即可;
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接即可;
(3)根据1米丝带的价格是4元,用单价×数量=总价,可求出购买7.5米丝带需要多少元;用总价÷单价=数量,可求得76元最多可以购买多长的丝带。
【详解】(1)应付金额与长度成正比例关系。
因为(一定),所以应付金额与长度成正比例关系。
(2)
(3)(元)
(米)
购买7.5米丝带需要30元;76元最多可以购买19长的丝带。
【点睛】熟练掌握正比例关系的定义,是解答此题的关键。
26.见详解
【分析】(1)根据表中的数据,进行描点、然后连线即可;
【详解】(1)单人票费:2÷1=2(元)
票费÷人数=单人票费(一定),所以票费与人数成正比例;
据此填表如下:
人数 0 1 2 3 4 5 6 7 8 …
票费/元 0 2 4 6 8 10 12 14 16 …
画图如下:
答:根据表中数据进行描点,我发现表格中的票费和人数是两种相关联的量,票费随着人数的变化而变化,票费与人数成正比例。连接各点后,发现是一条经过原点的直线。
(2)利用自己画的图,把下表填完整。
根据单人票费×人数=票费,人数=票费÷单人票费,可得:
16×2=32(元)
36÷2=18(人)
25×2=50(元)
56÷2=28(人)
60÷2=30(人)
66÷2=33(人)
由此填写下列表格:
人数 16 18 25 28 30 33
票费/元 32 36 50 56 60 66
【点睛】本题主要考查比例在日常生活中的应用,要正确判断哪两种量成什么比例。考查了学生综合运用知识解决问题的能力。【来源:21·世纪·教育·网】
27.见详解
【分析】(1)已知要生产240个零件,当工作效率为48个每小时的时候,可计算得出工作时间为240÷48=5(小时);当工作效率为40个每小时的时候,可计算得出工作时间为240÷40=6(小时);且由此能够总结出:工作时间是随着工作效率的变化而变化的;
(2)120×2=240(个)
80×3=240(个)
60×4=240(个)
48×5=240(个)
40×6=240(个)
(3)工作时间乘上每小时加工零件的个数,乘积就表示共生产240个零件,即工作总量;这三者的关系可表示为:工作效率×工作时间=工作总量;2-1-c-n-j-y
(4)要判断两个相关联的量是否成反比例,可看这两种量的乘积是否一定,如果一定,就是成反比例。
【详解】生产240个零件,工作效率和工作时间如下表。
工作效率(个/时) 120 80 60 48 40 …
工作时间/时 2 3 4 5 6 …
(1)工作时间是随着工作效率的变化而变化的;
(2)相对应的两个数的乘积是240;
(3)这个乘积的实际意义是生产240个零件,工作效率×工作时间=工作总量;
(4)工作效率和工作时间成反比例。因为工作效率和工作时间是两个相关联的两个量,并且工作时间随着工作效率的变化而变化,工作效率×工作时间=工作总量(一定)。所以,工作效率和工作时间成反比例。【出处:21教育名师】
【点睛】通过对表格的解读,能够使学生们进一步理解反比例的意义;并在此基础之上结合具体数据及数量关系来判断题目所涉及的两种量是否成反比例。【版权所有:21教育】
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
第四单元正比例与反比例(提升卷)
2024-2025学年六年级数学下册常考易错题(北师大版)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.淘气和爸爸的年龄变化情况如下表,下面描述错误的是( )。
淘气的年龄/岁 6 7 8 9
爸爸的年龄/岁 32 33 34 35
A.淘气和爸爸的年龄都在增加
B.淘气和爸爸的年龄差不变
C.淘气的年龄和爸爸的年龄成正比例关系
2.一列火车,4小时行320千米。照这样的速度,从甲城到乙城有420千米,( )小时可以到达?如果火车速度提高5%,( )小时就可以到达。( )
A.2.25;2 B.8.25;8 C.5.25;5 D.6.25;4
3.松树村的特菜生产基地,5天平整土地1.2公顷。照这样的效率,再工作2天,一共可以平整土地( )。
A.0.48公顷 B.8.16公顷 C.1.68公顷 D.16.8公顷
4.松树村特菜生产基地,计划平整1.68公顷土地,5天平整了1.2公顷。照这样的效率,剩下的任务还要( )天完成。
A.2 B.1 C.4 D.3
5.自然数和它的倒数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
二、填空题
6.判断下面的两个量成不成比例,如果成分别成什么比例,写在括号里。
打疫苗时,每小时打疫苗的人数一定,打疫苗的总人数与所用时间( )。
7.自行车前齿轮有48齿,后齿轮有16齿。当前齿轮转5圈时,后齿轮转( )圈。
8.在一定时间范围内,人的体重会随着年龄的增长而( )。
9.a÷b=c(a,b,c均不为0),当c一定时,a和b成( );当a一定时,b和c成( );当b一定时,a和c成( )。
10.把300mL的水倒入底面积不同的杯子中。
底面积/cm2 10 15 20 30 60
高度/cm 30 20 15 10 5
体积/cm3 300 300 300 300 300
从表中可以看出:( )随着( )的增加而( ),( )随着( )的减少而( )。
11.淘气今年12岁,张老师今年28岁。当淘气28岁时,张老师( )岁;当张老师60岁退休的时候,淘气( )岁。用字母m表示淘气的年龄,n表示张老师的年龄,m和n两个量之间的关系可以用式子( )表示。
12.一辆汽车油箱里储油102升,行驶了56千米正好耗油8升。照这样计算,剩下的油还可以行驶( )千米。
13.有一种花布,如图反映了购买的米数和应付钱数的关系。
(1)由图可见,购买米数和应付的钱数成( )比例。
(2)从图中可知,24元可买( )米布,买8米布应付( )元。
14.下表中m与n是两种成正比例的量,请你将表格填写完整。
m 8 20 656
n 0.4 4.8 20.4
三、判断题
15.做10道计算题,做对的题数和做错的题数成反比例。( )
16.正方形面积一定,它的一条边长与另一条边长成反比例。( )
17.正方形的边长和面积成正比例。( )
四、作图题
18.乘船的人数与所付船费如下表。
人数 0 1 2 3 4 5 6 7 …
船费/元 0 5 10 15 …
(1)把上表填写完整。
(2)所付船费与乘船人数成正比例吗?
(3)先根据上表描点,再顺次连接各点,你发现了什么?
(4)点(8,40)在这条直线上吗?这一点表示什么含义?
五、解答题
19.截至2002年年底,我国探明可直接利用的煤炭储量为2298.86亿吨。我国煤炭年均开采量与可开采年数之间的关系如下表。21*cnjy*com
年均开采量/亿吨 2 4 8 10 20 …
可开采年数 1149.43 574.715 287.3575 229.886 114.943 …
判断我国煤炭年均开采量与可开采年数之间是否成反比例,并说明理由。
20.一辆汽车行驶的路程和时间的情况如表。
时间/时 0 1 2 3 4 5
路程/千米 0 80 160 240 ( ) ( )
(1)把表填写完整。
(2)这辆汽车行驶的时间和路程成( )比例。
(3)先根据上表描点,再顺次连接各点。我发现所描的点都在同一条( )上。
(4)点(10,800)( )这条直线上。(填“在”或“不在”)
21.下面的图象反映的是美美和静静的睡眠情况。
(1)美美的睡眠时间和天数是否成正比例?静静的呢?为什么?
(2)美美和静静7天分别能睡多少时?
22.水是生命之源。向阳小学对同学们进行了节约用水教育。苗苗测试了一个打开的水龙头的流水量,测试结果如下表所示。2·1·c·n·j·y
时间/秒 0 10 20 30 40
出水量/L 0 2 4 6 8
(1)表中的时间和出水量是否成正比例,为什么?
(2)先根据上表中的数据描点,再顺次连接各点。
(3)看图估计,这个水龙头45秒的出水量是多少?
23.书籍是人类进步的阶梯,让课外书为孩子们打开一扇扇窗,开启一道道门。文明小学在五月中旬开展了“携手经典,浸润和美”的读书节活动。六(1)班的三名同学同读一本书,下表记录了每人每天看的页数和所需时间。www.21-cn-jy.com
(1)把表格补充完整。
李欢 孙林 董芊宜
每天看的页数 15 20 30
看完所需时间/天 8
(2)三名同学看书的过程中哪个量没变?每天看的页数和看完所需的天数有什么关系?
(3)看了3天后,他们已看的页数和剩下的页数成反比例吗?为什么?
24.一辆汽车的行驶路程和耗油量如下表。
路程/千米 10 20 30 40 50 …
耗油量/升 1.2 2.4 3.6 4.8 6.0 …
(1)观察上表,汽车的行驶路程和耗油量成( )比例。
(2)上图是这辆汽车出发时和到达时的油表,这辆汽车大约行驶了多少千米?(用比例解)
25.购买一种丝带的长度和应付金额如下表。
长度 0 1 2 3 4 5 …
应付金额元 0 4 8 12 16 20 …
(1)判断应付金额与长度是否成正比例关系,说明理由。
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接。
(3)购买7.5米丝带需要( )元;76元最多可以购买( )长的丝带。
26.看电影的人数与所付票费如下表。
人数 0 1 2 3 4 5 6 7 8 …
票费/元 0 2 4 6 …
(1)通过自己画图并连接各点,你发现了什么?
(2)利用自己画的图,把下表填完整。
人数 16 25
票费/元 36 56 60 66
27.生产240个零件,工作效率和工作时间如下表。
工作效率(个/时) 120 80 60 48 40 …
工作时间/时 2 3 4 …
(1)填写上表,工作时间是随着哪个量的变化而变化的?
(2)相对应的两个数的乘积各是多少?
(3)这个乘积的实际意义是什么?你能用式子表示出它与工作效率、工作时间之间的关系吗?
(4)工作效率和工作时间成反比例吗?为什么?
《第四单元正比例与反比例(提升卷)-2024-2025学年六年级数学下册常考易错题(北师大版)》参考答案21·世纪*教育网
1.C
【分析】淘气和爸爸的年龄每年都增加1岁,但年龄差不变;如果相对应的两个量x和y的比值一定,那么这两个量的关系成正比例关系,二人年龄的比值可以通过计算来得出结果,明显不是固定的。21*cnjy*com
【详解】A.从表中数据可以看出,淘气和爸爸的年龄都在增加,说法正确。
B.32-6=33-7=34-8=35-9=26(岁)
二人的年龄差为26岁,说法正确。
C.6∶32==
7∶33=
8∶34==
9∶35=
比值不相等,所以淘气和爸爸的年龄不成正比例,说法错误。
故答案为:C
【点睛】本题考查了正比例的意义的理解和灵活应用,同时考查了学生分析解决问题的能力。
2.C
【分析】根据题意可知,路程÷时间=速度(一定),则路程和时间的比值一定,它们成正比例关系,据此设从甲城到乙城有420千米,x小时可以到达,列比例为420∶x=320∶4,然后解出比例即可;先用320÷4求出火车的速度,如果火车速度提高5%,则把原来火车的速度看作单位“1”,现在火车的速度是原来的(1+5%),根据百分数乘法的意义,用原来的速度乘(1+5%)即可求出现在的速度,然后用420千米除以现在火车的速度,即可求出如果火车速度提高5%,几小时就可以到达。21教育名师原创作品
【详解】解:设从甲城到乙城有420千米,x小时可以到达。
420∶x=320∶4
320x=420×4
320x=1680
x=1680÷320
x=5.25
320÷4=80(千米/小时)
80×(1+5%)
=80×1.05
=84(千米/小时)
420÷84=5(小时)
从甲城到乙城有420千米,5.25小时可以到达;如果火车速度提高5%,5小时就可以到达。
故答案为:C
【点睛】本题主要考查了正比例的应用,掌握速度、时间、路程三者之间的关系是解答本题的关键。
3.C
【分析】根据题意可知,平整土地的总公顷数÷天数=每天平整土地的公顷数(一定),平整土地的总公顷数和天数的比值一定,它们成正比例;据此设2天可以平整土地x公顷,列比例为:x∶2=1.2∶5,然后解出比例即可。21·cn·jy·com
【详解】解:设2天可以平整土地x公顷。
x∶2=1.2∶5
5x=1.2×2
5x=2.4
x=2.4÷5
x=0.48
0.48+1.2=1.68(公顷)
照这样的效率,再工作2天,一共可以平整土地1.68公顷。
故答案为:C
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
4.A
【分析】根据题意可知,平整土地的总公顷数÷天数=每天平整土地的公顷数(一定),则平整土地的总公顷数和天数的比值一定,它们成正比例关系,据此设剩下的任务还要x天完成,列比例为(1.68-1.2)∶x=1.2∶5,然后解出比例即可。【来源:21cnj*y.co*m】
【详解】解:设剩下的任务还要x天完成。
(1.68-1.2)∶x=1.2∶5
0.48∶x=1.2∶5
1.2x=0.48×5
1.2x=2.4
x=2.4÷1.2
x=2
剩下的任务还要2天完成。
故答案为:A
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
5.B
【分析】根据倒数的意义(乘积是1的两个数互为倒数),由此可知:任何一个自然数(0除外)和它的倒数的乘积都是1,即这两个数的乘积一定,据此进行判断。
【详解】因为0没有倒数,所以这个自然数m不包括0,又因为:自然数m×它的倒数=1(一定),即对应的乘积一定,所以这个自然数m与它的倒数成反比例。
故答案为:B
【点睛】解答此题的关键是明白:两个量的积或者商一定,就说这两个量成反比例或正比例。
6.成正比例
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系。据此解答。
【详解】打疫苗的总人数÷所用的时间=每小时打疫苗的人数(一定),因此打疫苗的总人数与所用时间成正比例。
【点睛】两种相关联的量,若其比值一定,两种量成正比例关系。
7.15
【分析】
根据自行车中前齿轮齿数×前齿轮的转数=后齿轮齿数×后齿轮的转数,设后齿轮转x圈,列出方程,求出方程的解即可。
【详解】设后齿轮转x圈。
16x=48×5
16x=240
x=240÷16
x=15
则后齿轮转15圈。
8.增加
【详解】如:
下表是小红6岁前的体重变化情况。
年龄 出生时 2岁 4岁 6岁
体重/千克 3.5 14.0 18.0 21.0
根据表格中的数据,发现小红6岁前的体重随年龄的增长而增加。
体重是随年龄的增长而增加的,所以它们是两个相关联的量
本题属于根据正比例的意义,判断两种相关联的成不成正比例,就看这两种量是否是一个量变化,另一个量也随着变化,并且变化方向相同;且这两种量是否是对应的比值一定,再做判断。本题中一个量变化,另一个量也随着变化,但是两种量对应的比值不是一定的,因此不是正比例。21教育网
由此可得:在一定时间范围内,人的体重会随着年龄的增长而增加。
9. 正比例 反比例 正比例
【分析】
两个相关联的量,一个量随着另外一个量的变化而变化,如果两个量的商是一个定值,则说明这两个量成正比例关系;如果两个量的乘积一定,则说明这两个量成反比例关系。
【详解】
a÷b=c,当c一定时,就是商一定,则a和b成正比例;
a÷b=c,即bc=a, 当a一定时,就是乘积一定,则b和c成反比例;
a÷b=c,即a÷c=b, 当b一定时,就是一定,则a和c成反比例;
10. 高度 底面积 减少 底面积 高度 增加
【分析】从统计表中可知:两个相关联的量,底面积和高成反比例关系。一个量增加,一个量就减少,两个量的积不变。据此解答。
【详解】(高度)随着(底面积)的增加而(减少),(底面积)随着(高度)的减少而(增加)。
【点睛】熟练掌握判断两个相关联的量之间成什么比例是解答的关键。
11. 44 44 n=16+m
【分析】张老师今年的年龄-淘气今年的年龄=两人年龄差,年龄差永不变,淘气年龄+年龄差=张老师年龄;张老师年龄-年龄差=淘气年龄;据此用字母表示出两年年龄之间的关系。
【详解】28-12=16(岁)
28+16=44(岁)
60-16=44(岁)
n=16+m(答案不唯一)
当淘气28岁时,张老师44岁;当张老师60岁退休的时候,淘气44岁。用字母m表示淘气的年龄,n表示张老师的年龄,m和n两个量之间的关系可以用式子n=16+m表示。
12.658
【分析】根据题意可知,汽车的行驶路程÷耗油量=每升行驶的路程(一定),则汽车的行驶路程和耗油量的比值一定,它们成正比例关系;设剩下的油还可以行驶x千米,列比例为x∶(102-8)=56∶8,然后解出比例即可。
【详解】解:设剩下的油还可以行驶x千米。
x∶(102-8)=56∶8
x∶94=56∶8
8x=56×94
8x=5264
x=5264÷8
x=658
剩下的油还可以行驶658千米。
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
13.(1)正
(2) 6 32
【分析】(1)直接观察图像可以看出购买米数和应付的钱数成正比例关系。
(2)根据图像,直接找出24元对应的米数即可;直接找出买8米布对应的钱数,据此解答。
【详解】(1)由图可见,购买米数和应付的钱数成正比例关系。
(2)从图中可知,24元可买6米布,买8米布应付32元。
【点睛】此题考查了正比例的应用,明确两个变化的量,如果比值一定则成正比例关系。
14.96;408;
1;32.8
【分析】
x÷y=k(一定),x和y成正比例关系,m与n是两种成正比例的量,说明m与n的商一定,通过第一组数据,先求出m与n的商,根据被除数÷商=除数,商×除数=被除数,分别计算出未知的量,填表即可。21cnjy.com
【详解】8÷0.4=20
20÷20=1、20×4.8=96、20×20.4=408、656÷20=32.8
m 8 20 96 408 656
n 0.4 1 4.8 20.4 32.8
15.×
【分析】两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】做10道计算题,做对的题数+做错的题数=10,和一定,则做对的题数和做错的题数不成比例。原题说法错误。21世纪教育网版权所有
故答案为:×
【点睛】掌握反比例的意义是解题的关键。
16.×
【分析】判断两个相关联的量成什么比例关系,关键是看它们的积一定还是比值一定。如果它们的积一定,则成反比例关系;如果它们的比值一定,则成正比例关系。题干中正方形的边长相等,所以不存在两个相关联的量,据此解答。
【详解】正方形的面积公式是:,面积一定,边长就一定,不存在两个相关联的量,不构成反比例关系。
故答案为:×
【点睛】熟练掌握反比例的概念以及正方形的特征是解答本题的关键。
17.×
【分析】两个相关联的量,当比值一定时,成正比例关系,据此解答。
【详解】正方形面积=边长×边长;边长= ,比值不一定,所以正方形边长和面积不成正比例。
原题干说法错误。
故答案为:×
【点睛】明确正比例的意义是解答本题的关键。
18.(1)见详解
(2)成正比例
(3)描点见详解:发现这些点在同一条直线上,表示这两种量成正比例关系
(4)在;当人数是8人时,船费是40元
【分析】(1)根据表格中的数据,船费与乘船人数之间的关系是每增加1人,船费增加5元。据此补充表格;
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量,它们的关系叫做正比例关系。据此判断;
(3)根据表格中的数据描点、连线,结合连接后的图像写出发现;
(4)根据(3)的直线进行判断,看点(8,40)是否在直线上,如果在直线上,这点表示当人数是8人时,船费是40元。www-2-1-cnjy-com
【详解】(1)
人数 0 1 2 3 4 5 6 7 …
船费/元 0 5 10 15 20 25 30 35 …
(2)5∶1=10∶2=15∶3=20∶4=25∶5…=5(一定),即船费∶人数=单价(一定),比值一定,所以所付船费与乘船人数成正比例;
(3)如图:
发现:这些点在同一条直线上,表示这两种量成正比例关系;
(4)点(8,40)在这条直线上,表示当人数是8人时,船费是40元。
19.成反比例;理由见详解
【分析】反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量成反比例关系。
【详解】2×1149.43=4×574.715=8×287.3575=10×229.886=20×114.943…=2298.86(一定)
答:我国煤炭年均开采量与可开采年数成反比例,因为我国煤炭年均开采量×可开采年数=总煤炭储量(一定),乘积一定,则我国煤炭年均开采量与可开采年数成反比例。
20.(1)320;400
(2)正
(3)直线
(4)在
【分析】(1)根据前几组数据分别计算出这辆汽车4小时和5小时行驶的路程,填入表中;
(2)根据时间与路程的比值一定,确定行驶的时间和路程成正比例;
(3)成正比例关系的图形是一条直线,所以各点都在这条直线上;
(4)求出10与800的比值,即可确定这个点在这条直线上。
【详解】(1)根据前几组数据可知,路程∶时间=80∶1,即这辆汽车1小时行驶80千米。
4×80=320(千米)
5×80=400(千米)
所以这辆汽车4小时行驶的路程是320千米、5小时行驶的路程是400千米。
(2)1∶80=
2∶160==
3∶240==
比值一定,这辆汽车行驶的时间和路程成正比例。
(3)汽车行驶的时间和路程成正比例关系,成正比例关系的图形是一条直线,所以各点都在同一条直线上。
(4)10∶800==,所以点(10,800)在这条直线上。
【点睛】比值一定的两个量是成正比例关系的量,对应的各点都在同一条直线上。
21.(1)见详解;
(2)70小时,56小时。
【分析】(1)两个相关联的量,一个量随着另外一个量的变化而变化,且两个量的商是一个定值,则说明这两个量成正比例关系。美美的睡眠时间是随着天数的变化而变化的。将图形中美美的睡眠时间和天数相除。20÷2=10、40÷4=10、60÷6=10、80÷8=10,发现睡眠时间和天数的商是一定的。则美美的睡眠时间和天数成正比例。同理,静静的睡眠时间和天数相除。16÷2=8、32÷4=8、48÷6=8、64÷8=8、80÷10=8。则静静的睡眠时间和天数成正比例。
(2)通过(1)问中可以得出美美睡眠时间和天数的比值是10,则7天的睡眠时间=10×天数。静静睡眠时间和天数的比值是8,则7天的睡眠时间=8×天数。
【详解】(1)美美的睡眠时间和天数成正比例,因为睡眠时间÷天数=10(一定);
静静的睡眠时间和天数成正比例,因为睡眠时间÷天数=8(一定)。
(2)美美:20÷2=10(小时) 10×7=70(小时)
静静:16÷2=8(小时) 8×7=56(小时)
答:美美睡70小时,静静睡56小时。
22.(1)成正比例;理由见详解;
(2)见详解
(3)9L
【分析】(1)根据表格判断出,出水量和时间的比值一定,所以表中的时间和出水量成正比例;
(2)根据表格的数据,描出对应的点,连线即可;
(3)根据图象可知,当时间为45秒时,出水量超过8L,但没有达到10L,所以估计出水量为9L。
【详解】(1)表中的出水量和时间成正比例。
理由:(一定),也就是出水量和时间的比值一定,所以出水量和时间成正比例。
(2)如图:
(3)看图估计,这个水龙头45秒的出水量是9L。
23.(1)6;4
(2)总页数;反比例关系
(3)不成;见详解
【分析】(1)三人看的是同一本书。将李欢每天看的页数乘8天,求出书的总页数。将书总页数除以孙林每天看的页数,求出看完需要多少天。同理求出,董芊宜看完这本书需要多少天;
(2)看书过程中,书的总页数不变。乘积一定的两个量成反比例关系;
(3)乘积一定的两个量成反比例关系,据此分析解题。
【详解】(1)15×8=120(页)
120÷20=6(天)
120÷30=4(天)
填表如下:
李欢 孙林 董芊宜
每天看的页数 15 20 30
看完所需时间/天 8 6 4
(2)每天看的页数×看完需要的天数=书的总页数(一定)
答:三名同学看书的过程中,书的总页数不变。每天看的页数和看完所需的天数成反比例关系。
(3)答:看了3天后,他们已看的页数和剩下的页数不成反比例。因为已看的页数+剩下的页数=书总页数(一定),和是一定的,但积不一定。
24.(1)正;(2)125千米
【分析】(1)根据题意可知,汽车的行驶路程÷耗油量=每升行驶的路程(一定),则汽车的行驶路程和耗油量的比值一定,它们成正比例关系;
(2)根据题意可知,从出发到到达时,一共消耗了(40-25)升油,设这辆汽车大约行驶了x千米,列比例为x∶(40-25)=10∶1.2,然后解出比例即可。
【详解】(1)10÷1.2=(千米/升)
20÷2.4=(千米/升)
30÷3.6=(千米/升)
……
汽车的行驶路程和耗油量的比值一定,它们成正比例关系;
(2)解:设这辆汽车大约行驶了x千米。
x∶(40-25)=10∶1.2
x∶15=10∶1.2
1.2x=15×10
1.2x=150
x=150÷1.2
x=125
答:这辆汽车大约行驶了125千米。
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
25.(1)见详解
(2)见详解
(3)30;19
【分析】(1)如果两个相关联的量的比值一定,那么这两个相关联的量成正比例关系,据此解答即可;
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接即可;
(3)根据1米丝带的价格是4元,用单价×数量=总价,可求出购买7.5米丝带需要多少元;用总价÷单价=数量,可求得76元最多可以购买多长的丝带。
【详解】(1)应付金额与长度成正比例关系。
因为(一定),所以应付金额与长度成正比例关系。
(2)
(3)(元)
(米)
购买7.5米丝带需要30元;76元最多可以购买19长的丝带。
【点睛】熟练掌握正比例关系的定义,是解答此题的关键。
26.见详解
【分析】(1)根据表中的数据,进行描点、然后连线即可;
【详解】(1)单人票费:2÷1=2(元)
票费÷人数=单人票费(一定),所以票费与人数成正比例;
据此填表如下:
人数 0 1 2 3 4 5 6 7 8 …
票费/元 0 2 4 6 8 10 12 14 16 …
画图如下:
答:根据表中数据进行描点,我发现表格中的票费和人数是两种相关联的量,票费随着人数的变化而变化,票费与人数成正比例。连接各点后,发现是一条经过原点的直线。
(2)利用自己画的图,把下表填完整。
根据单人票费×人数=票费,人数=票费÷单人票费,可得:
16×2=32(元)
36÷2=18(人)
25×2=50(元)
56÷2=28(人)
60÷2=30(人)
66÷2=33(人)
由此填写下列表格:
人数 16 18 25 28 30 33
票费/元 32 36 50 56 60 66
【点睛】本题主要考查比例在日常生活中的应用,要正确判断哪两种量成什么比例。考查了学生综合运用知识解决问题的能力。【来源:21·世纪·教育·网】
27.见详解
【分析】(1)已知要生产240个零件,当工作效率为48个每小时的时候,可计算得出工作时间为240÷48=5(小时);当工作效率为40个每小时的时候,可计算得出工作时间为240÷40=6(小时);且由此能够总结出:工作时间是随着工作效率的变化而变化的;
(2)120×2=240(个)
80×3=240(个)
60×4=240(个)
48×5=240(个)
40×6=240(个)
(3)工作时间乘上每小时加工零件的个数,乘积就表示共生产240个零件,即工作总量;这三者的关系可表示为:工作效率×工作时间=工作总量;2-1-c-n-j-y
(4)要判断两个相关联的量是否成反比例,可看这两种量的乘积是否一定,如果一定,就是成反比例。
【详解】生产240个零件,工作效率和工作时间如下表。
工作效率(个/时) 120 80 60 48 40 …
工作时间/时 2 3 4 5 6 …
(1)工作时间是随着工作效率的变化而变化的;
(2)相对应的两个数的乘积是240;
(3)这个乘积的实际意义是生产240个零件,工作效率×工作时间=工作总量;
(4)工作效率和工作时间成反比例。因为工作效率和工作时间是两个相关联的两个量,并且工作时间随着工作效率的变化而变化,工作效率×工作时间=工作总量(一定)。所以,工作效率和工作时间成反比例。【出处:21教育名师】
【点睛】通过对表格的解读,能够使学生们进一步理解反比例的意义;并在此基础之上结合具体数据及数量关系来判断题目所涉及的两种量是否成反比例。【版权所有:21教育】
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
