6.5事件的概率(同步练习)(无答案)2024-2025学年九年级下册青岛版数学
文档属性
| 名称 | 6.5事件的概率(同步练习)(无答案)2024-2025学年九年级下册青岛版数学 |  | |
| 格式 | docx | ||
| 文件大小 | 45.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 09:33:29 | ||
图片预览

文档简介
6. 5事件的概率
(1)若随机抽取若干名同学做 “是否喜欢足球 ”的问卷调查 ,抽到喜欢足球的同学的概率是 ,这个的
含义是( ) .
A. 只发出了 5 份问卷 ,其中 3份是喜欢足球的
B. 在问卷中 ,喜欢足球的问卷与总问卷的比是 3 ∶ 8
C. 在问卷中 ,喜欢足球的问卷占总答卷的
D. 在问卷中 ,每抽出 100份 ,恰有 60份是不喜欢足球的
(2)现要在一只口 袋 中 装 入 若 干 个 形 状 与 大 小 都 完 全 相 同 的 球 , 使 得 从 该 口 袋 中 摸 到 红 球 的 概 率 为
. 四位同学分别采用了下列装法 ,你认为他们中装错的是( ) .
A. 装入 10个球 ,其中只有 2个红球
B. 装入 1个红球 ,1个白球 ,1个黄球 ,1个蓝球 ,1个黑球
C. 装入 5个红球 ,13个白球 ,2个黑球
D. 装入 7个红球 ,13个白球 ,2个黑球 ,13个黄球
(3)某学生调查了同班同学身上的零用钱 ,并计数据记录如下(单位 : 元) . 2, 5,0, 5, 2, 5, 6, 5,0, 5, 5, 5, 2,5,8,0,5,5,2,5,5,8,6,5,2,5,5,2, 5, 6, 5, 5,0, 6, 5, 6, 5,2, 5,0. 假如老师随机问一名学生身上有多少零 用钱 ,老师最有可能得到的回答是( ) .
A.2元 B.5元 C.6元 D.0元
(1)儿童节期间 ,某玩具超市设立了一个如图 6-5-3所示的自由转盘 ,开展有奖购买活动 . 顾客购买玩具 就能获得一次转动转盘的机会 , 当转盘停止时 ,指针落在哪一区域就可以获得相应奖品 . 下表是该活动的 一 组统计数据 .
1
转动转盘的次数(n) 100 150 200 500 800 1000
落在 “铅笔 ”区域的次数(m) 68 108 140 355 560 690
落在 “铅笔 ”区域的频率 0. 68 0. 72 0. 70 0. 71 0. 70 0. 69
下列说法中不正确的是( ) .
A. 当 n很大时 ,估计指针落在 “铅笔 ”区域的频率大约是 0. 70
B. 假如你去转动转盘 1 次 ,获得铅笔的概率大约是 0. 70
C. 如果转动转盘 2000次 ,指针落在 “文具盒 ”区域的次数大约有 600次
D. 转动转盘 10次 ,一定有 3 次获得文具盒
图 6-5-3
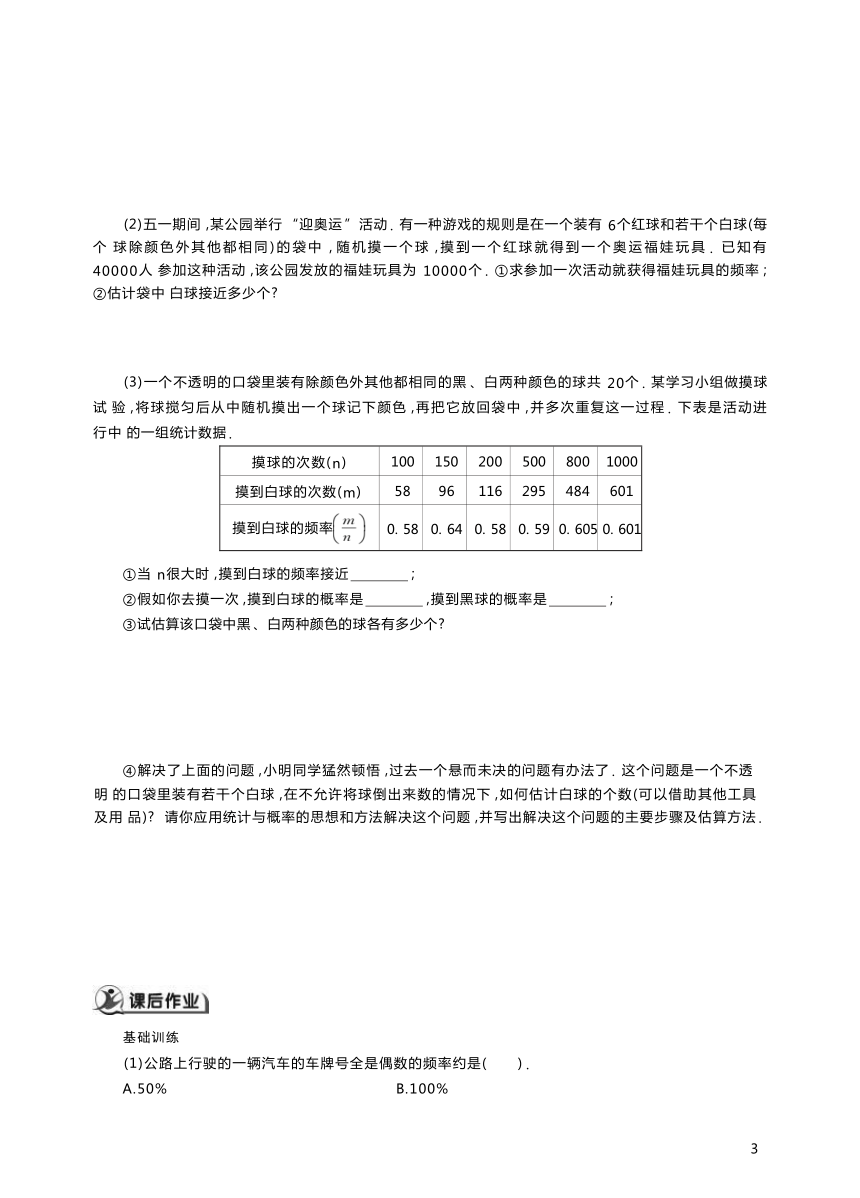
(2)五一期间 ,某公园举行 “迎奥运 ”活动 . 有一种游戏的规则是在一个装有 6个红球和若干个白球(每个 球除颜色外其他都相同)的袋中 , 随机摸一个球 ,摸到一个红球就得到一个奥运福娃玩具 . 已知有 40000人 参加这种活动 ,该公园发放的福娃玩具为 10000个 . ①求参加一次活动就获得福娃玩具的频率 ; ②估计袋中 白球接近多少个
(3)一个不透明的口袋里装有除颜色外其他都相同的黑 、白两种颜色的球共 20个 . 某学习小组做摸球试 验 ,将球搅匀后从中随机摸出一个球记下颜色 ,再把它放回袋中 ,并多次重复这一过程 . 下表是活动进行中 的一组统计数据 .
摸球的次数(n) 100 150 200 500 800 1000
摸到白球的次数(m) 58 96 116 295 484 601
摸到白球的频率 0. 58 0. 64 0. 58 0. 59 0. 605 0. 601
①当 n很大时 ,摸到白球的频率接近 ;
②假如你去摸一次 ,摸到白球的概率是 ,摸到黑球的概率是 ;
③试估算该口袋中黑 、白两种颜色的球各有多少个
④解决了上面的问题 ,小明同学猛然顿悟 ,过去一个悬而未决的问题有办法了 . 这个问题是一个不透明 的口袋里装有若干个白球 ,在不允许将球倒出来数的情况下 ,如何估计白球的个数(可以借助其他工具及用 品) 请你应用统计与概率的思想和方法解决这个问题 ,并写出解决这个问题的主要步骤及估算方法 .
基础训练
(1)公路上行驶的一辆汽车的车牌号全是偶数的频率约是( ) .
A.50% B.100%
C. 由各车所在单位或个人决定 D. 无法确定 (2)关于频率和概率的关系 ,下列说法中正确的是( ) .
A. 频率等于概率
B. 当试验次数很大时 ,频率稳定在概率附近 C. 当试验次数很大时 ,概率稳定在频率附近 D. 试验得到的频率与概率不可能相等
(3)下列说法中正确的是( ) .
A. 某事件发生的概率为这就是说在两次重复试验中 ,必有一次发生
B. 一个袋子里装有 100个球 ,小明摸了 8次 ,每次都只摸到黑球 ,没摸到白球 ,则袋子里只有黑球
C. 将两枚一元的硬币同时抛下 ,可能出现的情形:①两枚均为正面朝上 ; ②两枚均为反面朝上 ; ③一枚
正面趄上 ,一枚反面朝上 ,所以出现一正一反的概率是
D. 全年级有 400名学生 ,一定有 2人同一天过生 日
(4)某灯泡厂在一次质量检查中 ,从 2000个灯泡中随机抽查了 100个 ,其中有 10个不合格 ,则出现不合格灯 泡的频率是 . 在这 2000个灯泡中 ,估计有 个为不合格产品.
(5)用 6个球(除颜色外没有其他区别)设计满足如下条件的游戏:摸到白球的概率为摸到红球的概 率为 ,摸到黄球的概率为 . 则应有 个白球 , 个红球 , 个黄球 .
(6)一副残缺的扑克牌 ,只有红心和黑桃两种花色的牌 ,并且缺 6 张 . 通过若干次试验知道红心和黑桃出 现的频率分别为 45%和 55% ,则共有红心牌 张 .
拓展提高
为估计某鱼塘中共有多少条鱼 ,王师傅从鱼塘中捕捞了 1000条鱼作上记号后又放回鱼塘 ,经过一段时
间 ,他再次从鱼塘中捕捞了 200条鱼 ,其中有标记的有 10条 ,估计鱼塘里有 条鱼 .
发散思维
(1)王强和小刚在学习 “概率 ”时 ,进行抛骰子(均匀的正方体形状)试验 ,他们共抛了 54次 , 出现向上面 点数的次数如下表 .
向上面点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
①计算向上面点数为 3 的频率及出现向上面点数为 5 的频率 ;
②王强说:“根据试验 ,一次试验中出现向上面点数为 5 的概率最大 . ”小刚说:“如果抛 540次 ,那么出现 向上面点数为 6 的次数正好是 100次 . ”请判断王强和小刚说法的对错 ;
③如果王强与小刚各抛一枚骰子 ,求出现向上面点数之和为 3 的倍数的概率 .
(2)某商场设计了两种促销方案 . 第一种:顾客在商场消费每满 200元 ,可从一个装有 100个完全相同的 球(球上分别标有数字 1,2, … ,100)的箱子中随机摸出一个球(摸后放回) . 若球上的数字是 88,则返购物券 500元 ;若球上的数字是 11或 77,则返购物券 300元 ;若球上的数字能被 5 整除 ,则返购物券 5元 ;若是其他 数字 ,则不返购物券 . 第 二 种:顾 客 在 商 场 消 费 每 满 200元 , 可 直 接 获 得 购 物 券 15元 . 估 计 促 销 期 间 将 有 5000人次参加该活动 ,请通过计算说明商家选择哪种促销方案更合算 .
3
(1)若随机抽取若干名同学做 “是否喜欢足球 ”的问卷调查 ,抽到喜欢足球的同学的概率是 ,这个的
含义是( ) .
A. 只发出了 5 份问卷 ,其中 3份是喜欢足球的
B. 在问卷中 ,喜欢足球的问卷与总问卷的比是 3 ∶ 8
C. 在问卷中 ,喜欢足球的问卷占总答卷的
D. 在问卷中 ,每抽出 100份 ,恰有 60份是不喜欢足球的
(2)现要在一只口 袋 中 装 入 若 干 个 形 状 与 大 小 都 完 全 相 同 的 球 , 使 得 从 该 口 袋 中 摸 到 红 球 的 概 率 为
. 四位同学分别采用了下列装法 ,你认为他们中装错的是( ) .
A. 装入 10个球 ,其中只有 2个红球
B. 装入 1个红球 ,1个白球 ,1个黄球 ,1个蓝球 ,1个黑球
C. 装入 5个红球 ,13个白球 ,2个黑球
D. 装入 7个红球 ,13个白球 ,2个黑球 ,13个黄球
(3)某学生调查了同班同学身上的零用钱 ,并计数据记录如下(单位 : 元) . 2, 5,0, 5, 2, 5, 6, 5,0, 5, 5, 5, 2,5,8,0,5,5,2,5,5,8,6,5,2,5,5,2, 5, 6, 5, 5,0, 6, 5, 6, 5,2, 5,0. 假如老师随机问一名学生身上有多少零 用钱 ,老师最有可能得到的回答是( ) .
A.2元 B.5元 C.6元 D.0元
(1)儿童节期间 ,某玩具超市设立了一个如图 6-5-3所示的自由转盘 ,开展有奖购买活动 . 顾客购买玩具 就能获得一次转动转盘的机会 , 当转盘停止时 ,指针落在哪一区域就可以获得相应奖品 . 下表是该活动的 一 组统计数据 .
1
转动转盘的次数(n) 100 150 200 500 800 1000
落在 “铅笔 ”区域的次数(m) 68 108 140 355 560 690
落在 “铅笔 ”区域的频率 0. 68 0. 72 0. 70 0. 71 0. 70 0. 69
下列说法中不正确的是( ) .
A. 当 n很大时 ,估计指针落在 “铅笔 ”区域的频率大约是 0. 70
B. 假如你去转动转盘 1 次 ,获得铅笔的概率大约是 0. 70
C. 如果转动转盘 2000次 ,指针落在 “文具盒 ”区域的次数大约有 600次
D. 转动转盘 10次 ,一定有 3 次获得文具盒
图 6-5-3
(2)五一期间 ,某公园举行 “迎奥运 ”活动 . 有一种游戏的规则是在一个装有 6个红球和若干个白球(每个 球除颜色外其他都相同)的袋中 , 随机摸一个球 ,摸到一个红球就得到一个奥运福娃玩具 . 已知有 40000人 参加这种活动 ,该公园发放的福娃玩具为 10000个 . ①求参加一次活动就获得福娃玩具的频率 ; ②估计袋中 白球接近多少个
(3)一个不透明的口袋里装有除颜色外其他都相同的黑 、白两种颜色的球共 20个 . 某学习小组做摸球试 验 ,将球搅匀后从中随机摸出一个球记下颜色 ,再把它放回袋中 ,并多次重复这一过程 . 下表是活动进行中 的一组统计数据 .
摸球的次数(n) 100 150 200 500 800 1000
摸到白球的次数(m) 58 96 116 295 484 601
摸到白球的频率 0. 58 0. 64 0. 58 0. 59 0. 605 0. 601
①当 n很大时 ,摸到白球的频率接近 ;
②假如你去摸一次 ,摸到白球的概率是 ,摸到黑球的概率是 ;
③试估算该口袋中黑 、白两种颜色的球各有多少个
④解决了上面的问题 ,小明同学猛然顿悟 ,过去一个悬而未决的问题有办法了 . 这个问题是一个不透明 的口袋里装有若干个白球 ,在不允许将球倒出来数的情况下 ,如何估计白球的个数(可以借助其他工具及用 品) 请你应用统计与概率的思想和方法解决这个问题 ,并写出解决这个问题的主要步骤及估算方法 .
基础训练
(1)公路上行驶的一辆汽车的车牌号全是偶数的频率约是( ) .
A.50% B.100%
C. 由各车所在单位或个人决定 D. 无法确定 (2)关于频率和概率的关系 ,下列说法中正确的是( ) .
A. 频率等于概率
B. 当试验次数很大时 ,频率稳定在概率附近 C. 当试验次数很大时 ,概率稳定在频率附近 D. 试验得到的频率与概率不可能相等
(3)下列说法中正确的是( ) .
A. 某事件发生的概率为这就是说在两次重复试验中 ,必有一次发生
B. 一个袋子里装有 100个球 ,小明摸了 8次 ,每次都只摸到黑球 ,没摸到白球 ,则袋子里只有黑球
C. 将两枚一元的硬币同时抛下 ,可能出现的情形:①两枚均为正面朝上 ; ②两枚均为反面朝上 ; ③一枚
正面趄上 ,一枚反面朝上 ,所以出现一正一反的概率是
D. 全年级有 400名学生 ,一定有 2人同一天过生 日
(4)某灯泡厂在一次质量检查中 ,从 2000个灯泡中随机抽查了 100个 ,其中有 10个不合格 ,则出现不合格灯 泡的频率是 . 在这 2000个灯泡中 ,估计有 个为不合格产品.
(5)用 6个球(除颜色外没有其他区别)设计满足如下条件的游戏:摸到白球的概率为摸到红球的概 率为 ,摸到黄球的概率为 . 则应有 个白球 , 个红球 , 个黄球 .
(6)一副残缺的扑克牌 ,只有红心和黑桃两种花色的牌 ,并且缺 6 张 . 通过若干次试验知道红心和黑桃出 现的频率分别为 45%和 55% ,则共有红心牌 张 .
拓展提高
为估计某鱼塘中共有多少条鱼 ,王师傅从鱼塘中捕捞了 1000条鱼作上记号后又放回鱼塘 ,经过一段时
间 ,他再次从鱼塘中捕捞了 200条鱼 ,其中有标记的有 10条 ,估计鱼塘里有 条鱼 .
发散思维
(1)王强和小刚在学习 “概率 ”时 ,进行抛骰子(均匀的正方体形状)试验 ,他们共抛了 54次 , 出现向上面 点数的次数如下表 .
向上面点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
①计算向上面点数为 3 的频率及出现向上面点数为 5 的频率 ;
②王强说:“根据试验 ,一次试验中出现向上面点数为 5 的概率最大 . ”小刚说:“如果抛 540次 ,那么出现 向上面点数为 6 的次数正好是 100次 . ”请判断王强和小刚说法的对错 ;
③如果王强与小刚各抛一枚骰子 ,求出现向上面点数之和为 3 的倍数的概率 .
(2)某商场设计了两种促销方案 . 第一种:顾客在商场消费每满 200元 ,可从一个装有 100个完全相同的 球(球上分别标有数字 1,2, … ,100)的箱子中随机摸出一个球(摸后放回) . 若球上的数字是 88,则返购物券 500元 ;若球上的数字是 11或 77,则返购物券 300元 ;若球上的数字能被 5 整除 ,则返购物券 5元 ;若是其他 数字 ,则不返购物券 . 第 二 种:顾 客 在 商 场 消 费 每 满 200元 , 可 直 接 获 得 购 物 券 15元 . 估 计 促 销 期 间 将 有 5000人次参加该活动 ,请通过计算说明商家选择哪种促销方案更合算 .
3
