华师大版八年级下册18.2平行四边形的判定课件(共21张PPT)
文档属性
| 名称 | 华师大版八年级下册18.2平行四边形的判定课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-13 00:00:00 | ||
图片预览



文档简介
课件21张PPT。平行四边形的判定边上判定性质1平行四边形的两组对边分别平行判定1两组对边分别平行的四边形
是平行四边形性质2平行四边形的两组对边分别相等判定2两组对边分别相等的四边形
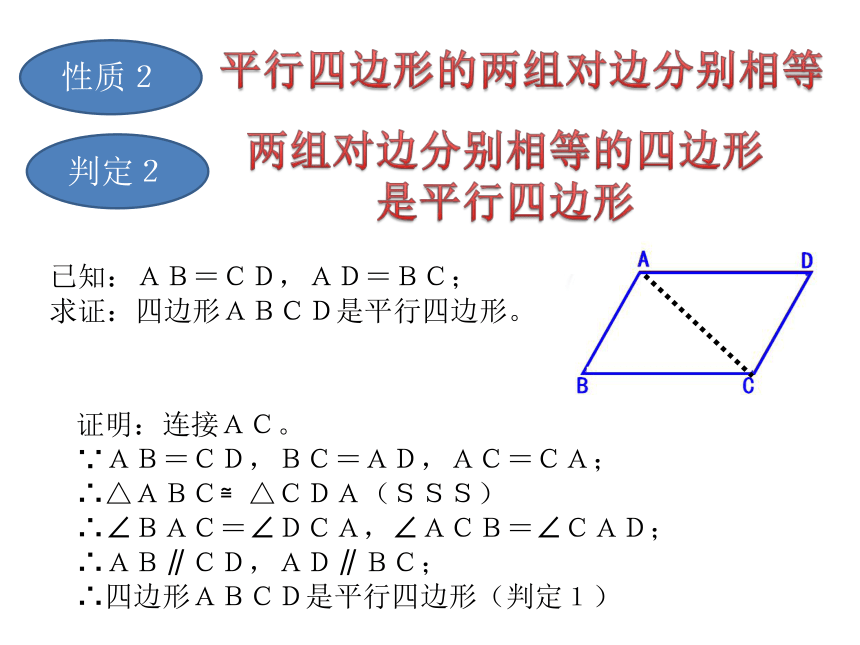
是平行四边形已知:AB=CD,AD=BC;
求证:四边形ABCD是平行四边形。证明:连接AC。
∵AB=CD,BC=AD,AC=CA;
∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD;
∴AB∥CD,AD∥BC;
∴四边形ABCD是平行四边形(判定1)判定3一组对边平行且相等的四边形
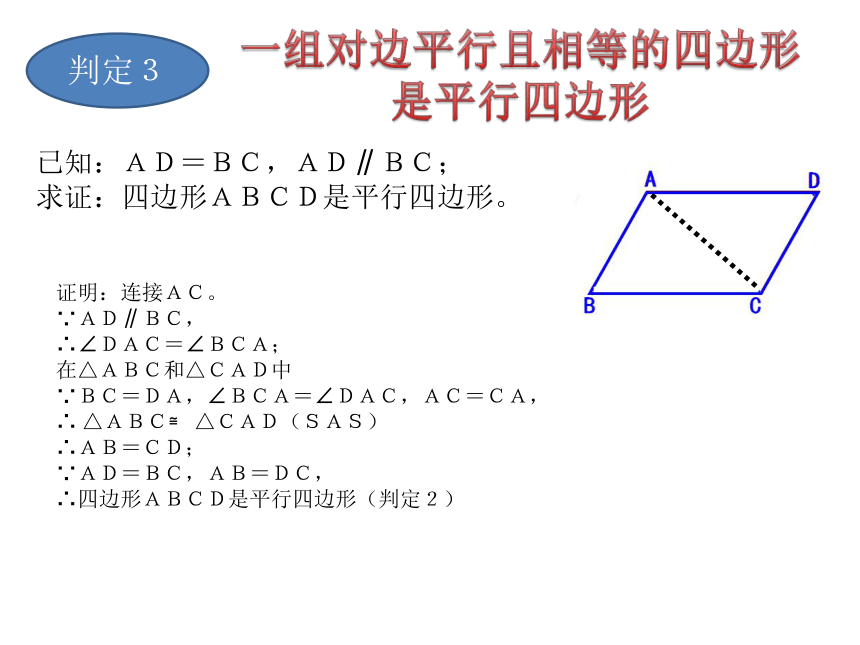
是平行四边形已知:AD=BC,AD∥BC;
求证:四边形ABCD是平行四边形。证明:连接AC。
∵AD∥BC,
∴∠DAC=∠BCA;
在△ABC和△CAD中
∵BC=DA,∠BCA=∠DAC,AC=CA,
∴ △ABC≌ △CAD(SAS)
∴AB=CD;
∵AD=BC,AB=DC,
∴四边形ABCD是平行四边形(判定2)角上判定性质3平行四边形的两组对角分别相等判定4两组对角分别相等的四边形
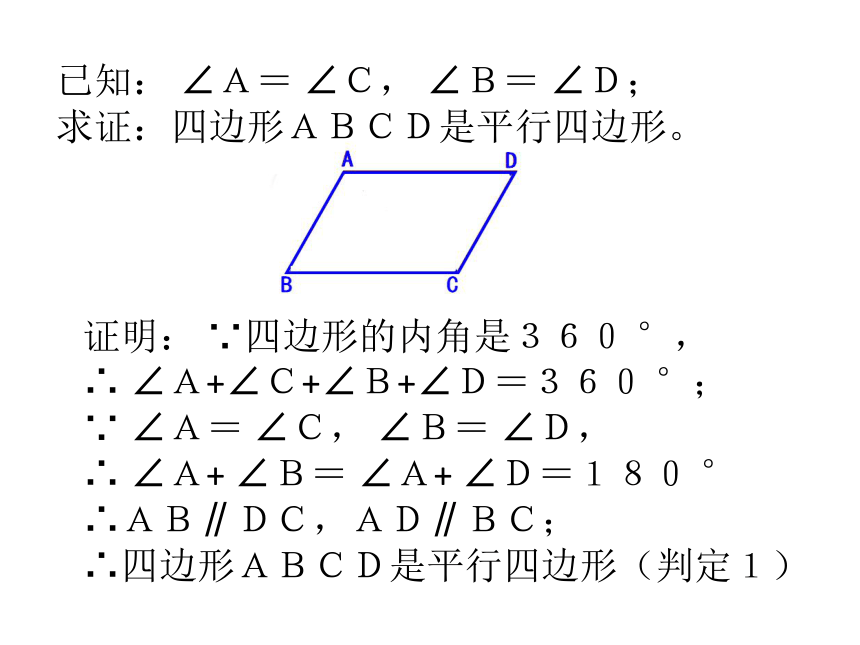
是平行四边形已知: ∠A= ∠C, ∠B= ∠D;
求证:四边形ABCD是平行四边形。证明: ∵四边形的内角是360 °,
∴ ∠A+∠C+∠B+∠D=360 °;
∵ ∠A= ∠C, ∠B= ∠D,
∴ ∠A+ ∠B= ∠A+ ∠D=180 °
∴AB∥DC,AD∥BC;
∴四边形ABCD是平行四边形(判定1)线上判定性质4平行四边形的两条对角线互相平分判定5两条对角线互相平分的四边形
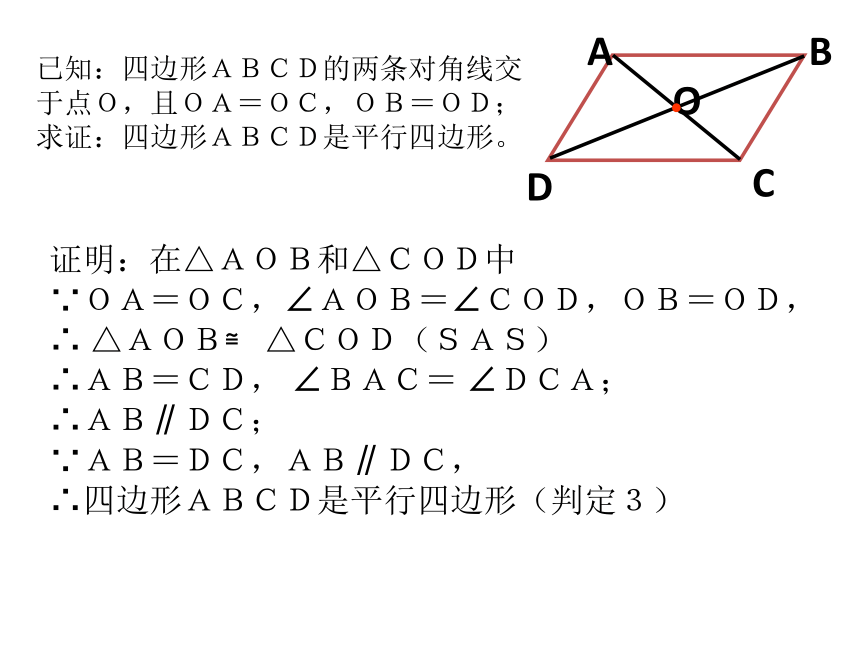
是平行四边形已知:四边形ABCD的两条对角线交于点O,且OA=OC,OB=OD;
求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中
∵OA=OC,∠AOB=∠COD,OB=OD,
∴ △AOB≌ △COD(SAS)
∴AB=CD, ∠BAC= ∠DCA;
∴AB∥DC;
∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形(判定3)例1.如图, 四边形ABCD中,已知AB∥CD,那么再添加一个条件_________,使得四边形ABCD是一个平行四边形.ADCB答案: AD∥BC或AB=BC
或∠A= ∠C或∠B= ∠D。例3. (宿迁·中考)如图,在□ ABCD中,点E,F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.【证明】∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形BEDF是平行四边形,
∴∠EBF=∠FDE.例4.(中山·中考)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知
∠BAC=30°,EF⊥AB,垂足为F,连结DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.【解析】(1)在Rt△ABC中,∠BAC=30°,
∴BC= AB,∴
在等边△ABE中,EF⊥AB,
∴
∴AC=EF.
(2)∵∠DAF=∠DAC+∠BAC=60°+30°=90°,∠EFA=90°,
∴AD∥EF,
又∵AC=AD=EF,
∴四边形ADFE是平行四边形.【例5】(2013·龙岩中考)如图,四边形ABCD是平行四边形,E,F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF.
(2)求证:四边形EBFD是平行四边形.(1)如图①:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4.
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2,
∴∠5=∠6,∴△ADE≌△CBF,∴AE =CF.(2)方法一:如图①,∵∠1=∠2,∴DE∥BF,
∵△ADE≌△CBF,∴DE=BF,
∴四边形EBFD是平行四边形.
方法二:如图②,连结BD.
∵AE=CF,∴OE=OF.又∵OB=OD,
∴四边形EBFD是平行四边形.【练习】
1.(2013·长春中考)如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连结AD,CD.若∠B=65°,则∠ADC的大小为 度.2、如图,在□ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
3、如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:(1)△AFD≌△CEB.
(2)四边形ABCD是平行四边形.
4.如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.5、如图所示,在 平行四边形ABCD中,E、F分别是AB 、 CD的中点.下图中有几个平行四边形? 请说明理由.6、如图,△ABC中,D是AB的中点,E是AC上的一点,EF∥AB,DF∥BE.
(1)猜想:DF与AE间的关系是 .
(2)请对你的猜想说明原因.7、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
8、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
是平行四边形性质2平行四边形的两组对边分别相等判定2两组对边分别相等的四边形
是平行四边形已知:AB=CD,AD=BC;
求证:四边形ABCD是平行四边形。证明:连接AC。
∵AB=CD,BC=AD,AC=CA;
∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD;
∴AB∥CD,AD∥BC;
∴四边形ABCD是平行四边形(判定1)判定3一组对边平行且相等的四边形
是平行四边形已知:AD=BC,AD∥BC;
求证:四边形ABCD是平行四边形。证明:连接AC。
∵AD∥BC,
∴∠DAC=∠BCA;
在△ABC和△CAD中
∵BC=DA,∠BCA=∠DAC,AC=CA,
∴ △ABC≌ △CAD(SAS)
∴AB=CD;
∵AD=BC,AB=DC,
∴四边形ABCD是平行四边形(判定2)角上判定性质3平行四边形的两组对角分别相等判定4两组对角分别相等的四边形
是平行四边形已知: ∠A= ∠C, ∠B= ∠D;
求证:四边形ABCD是平行四边形。证明: ∵四边形的内角是360 °,
∴ ∠A+∠C+∠B+∠D=360 °;
∵ ∠A= ∠C, ∠B= ∠D,
∴ ∠A+ ∠B= ∠A+ ∠D=180 °
∴AB∥DC,AD∥BC;
∴四边形ABCD是平行四边形(判定1)线上判定性质4平行四边形的两条对角线互相平分判定5两条对角线互相平分的四边形
是平行四边形已知:四边形ABCD的两条对角线交于点O,且OA=OC,OB=OD;
求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中
∵OA=OC,∠AOB=∠COD,OB=OD,
∴ △AOB≌ △COD(SAS)
∴AB=CD, ∠BAC= ∠DCA;
∴AB∥DC;
∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形(判定3)例1.如图, 四边形ABCD中,已知AB∥CD,那么再添加一个条件_________,使得四边形ABCD是一个平行四边形.ADCB答案: AD∥BC或AB=BC
或∠A= ∠C或∠B= ∠D。例3. (宿迁·中考)如图,在□ ABCD中,点E,F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.【证明】∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形BEDF是平行四边形,
∴∠EBF=∠FDE.例4.(中山·中考)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知
∠BAC=30°,EF⊥AB,垂足为F,连结DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.【解析】(1)在Rt△ABC中,∠BAC=30°,
∴BC= AB,∴
在等边△ABE中,EF⊥AB,
∴
∴AC=EF.
(2)∵∠DAF=∠DAC+∠BAC=60°+30°=90°,∠EFA=90°,
∴AD∥EF,
又∵AC=AD=EF,
∴四边形ADFE是平行四边形.【例5】(2013·龙岩中考)如图,四边形ABCD是平行四边形,E,F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF.
(2)求证:四边形EBFD是平行四边形.(1)如图①:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4.
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2,
∴∠5=∠6,∴△ADE≌△CBF,∴AE =CF.(2)方法一:如图①,∵∠1=∠2,∴DE∥BF,
∵△ADE≌△CBF,∴DE=BF,
∴四边形EBFD是平行四边形.
方法二:如图②,连结BD.
∵AE=CF,∴OE=OF.又∵OB=OD,
∴四边形EBFD是平行四边形.【练习】
1.(2013·长春中考)如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连结AD,CD.若∠B=65°,则∠ADC的大小为 度.2、如图,在□ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
3、如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:(1)△AFD≌△CEB.
(2)四边形ABCD是平行四边形.
4.如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.5、如图所示,在 平行四边形ABCD中,E、F分别是AB 、 CD的中点.下图中有几个平行四边形? 请说明理由.6、如图,△ABC中,D是AB的中点,E是AC上的一点,EF∥AB,DF∥BE.
(1)猜想:DF与AE间的关系是 .
(2)请对你的猜想说明原因.7、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
8、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
