华师大版八年级下册18.1平行四边形的性质课件(共27张PPT)
文档属性
| 名称 | 华师大版八年级下册18.1平行四边形的性质课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-13 08:24:09 | ||
图片预览





文档简介
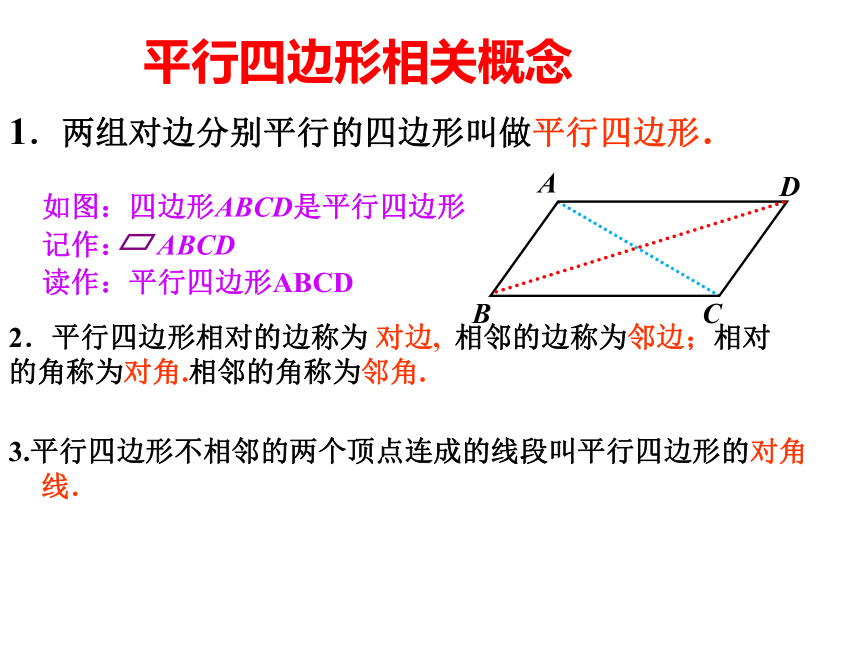
课件27张PPT。18.1平行四边形的性质这些图片中,有你熟悉的图形吗?返回1.两组对边分别平行的四边形叫做平行四边形.如图:四边形ABCD是平行四边形
记作: ABCD
读作:平行四边形ABCD
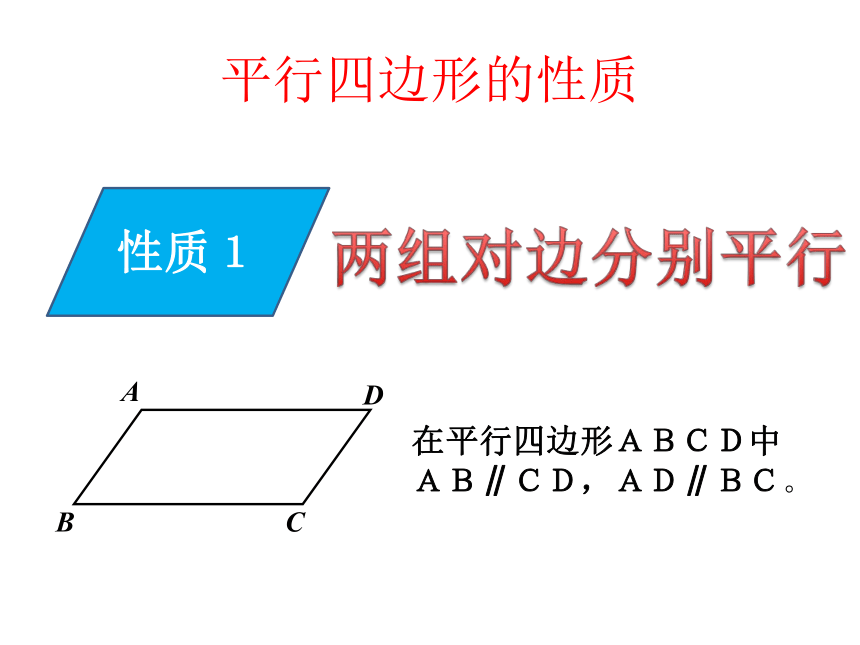
2.平行四边形相对的边称为 对边, 相邻的边称为邻边;相对的角称为对角.相邻的角称为邻角.3.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.平行四边形相关概念平行四边形的性质性质1两组对边分别平行在平行四边形ABCD中
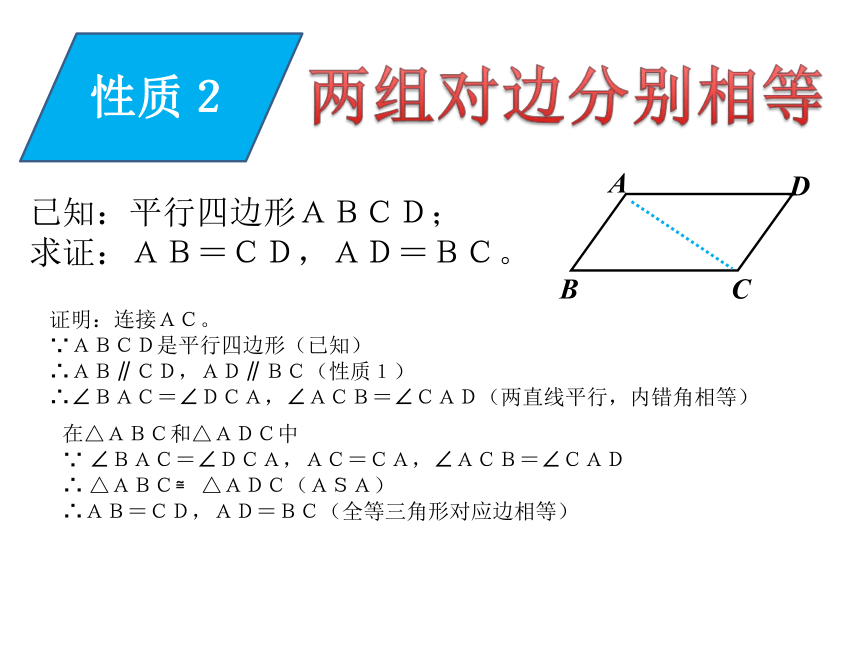
AB∥CD,AD∥BC。性质2两组对边分别相等已知:平行四边形ABCD;
求证:AB=CD,AD=BC。证明:连接AC。
∵ABCD是平行四边形(已知)
∴AB∥CD,AD∥BC(性质1)
∴∠BAC=∠DCA,∠ACB=∠CAD(两直线平行,内错角相等)在△ABC和△ADC中
∵ ∠BAC=∠DCA,AC=CA,∠ACB=∠CAD
∴ △ABC≌ △ADC(ASA)
∴AB=CD,AD=BC(全等三角形对应边相等)性质3两组对角分别相等已知:平行四边形ABCD;
求证: ∠A= ∠C, ∠B= ∠D。证明:∵ABCD是平行四边形(已知)
∴AB∥CD,AD∥BC(性质1)
∴∠A+∠D=180°, ∠A+∠B=180°(两直线平行,同旁内角互补)
∴ ∠B= ∠D(同角的补角相等)
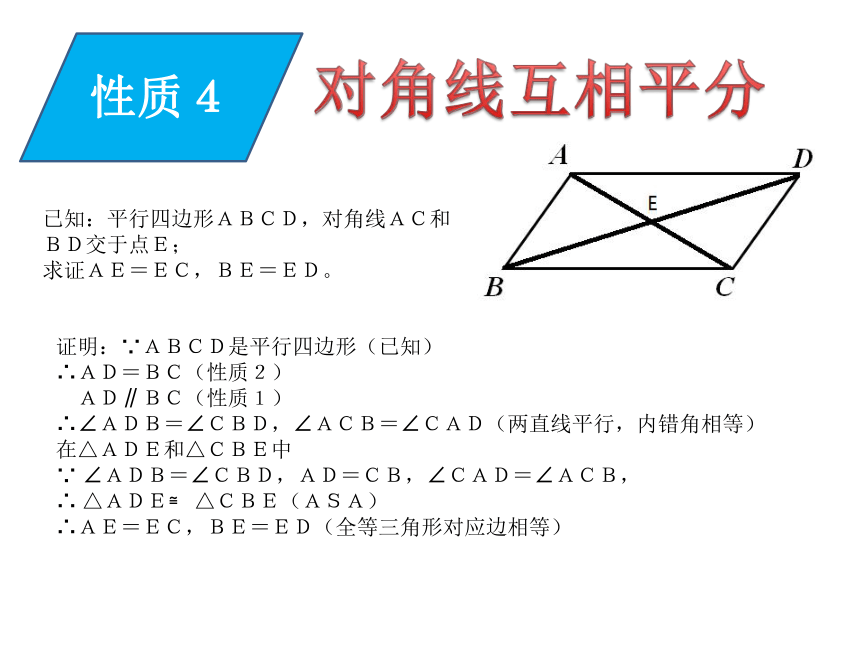
同理可证∠A= ∠C性质4对角线互相平分已知:平行四边形ABCD,对角线AC和BD交于点E;
求证AE=EC,BE=ED。证明:∵ABCD是平行四边形(已知)
∴AD=BC(性质2)
AD∥BC(性质1)
∴∠ADB=∠CBD,∠ACB=∠CAD(两直线平行,内错角相等)
在△ADE和△CBE中
∵ ∠ADB=∠CBD,AD=CB,∠CAD=∠ACB,
∴ △ADE≌ △CBE(ASA)
∴AE=EC,BE=ED(全等三角形对应边相等)性质5是中心对称图形已知:平行四边形ABCD;
求证:ABCD是中心对称图形。证明:∵ABCD是平行四边形(已知)
∴AE=EC,BE=ED(性质4)
∴A与C关于E成中心对称,B与D关于E成中心对称(中心对称的性质)
∴平行四边形ABCD关于E成中心对称。
平行四边形的性质几何语言:两组对边分别平行且相等∵ 四边形ABCD是平行四边形∴ AB∥CD,AD∥BC. (平行四边形的对边平行)
AB=CD, AD=BC (平行四边形的对边相等)∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) AE= EC, BE= ED(平行四边形的对角线互相平分) 两组对角分别相等对角线互相平分是中心对称图形例题解析例1、在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别是E和F,求证:AE=CF证明:∵ 四边形ABCD是平行四边形
∴AD=BC,∠A= ∠C∵ DE⊥AB,BF⊥CD
∴∠AED= ∠CFB
在△ADE和△CBF中∠A=∠C
∠AED=∠CFB
AD=BC∴ △ADE≌△CBF(AAS)∴ AE=CF平行线间的距离处处相等1、如图在A基础知识:(1)若AB=1㎝,BC=2 ㎝B变式训练:(2)若AB:BC=3:4,周长为14㎝,则CD=——,DA=——(1)若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____6cm5cm3cm4cm8cm28cm边的运算A.6cm B.12cm C.4cm D.8cmABDC2.如图, □ABCD的周长是28cm,△ABC的周长是22cm,则
AC的长为( )D3.(广州·中考)已知□ABCD的周长为32,AB=4,则BC=( )
A. 4 B. 12 C. 24 D. 28【解析】选B.根据平行四边形的性质可以得出AB=CD,BC=AD,又因AB+CD+BC+AD=32,所以BC=12.4.(河北?中考)如图,在□ ABCD中,AC平分
∠DAB,AB=3,则□ ABCD的周长为( )
A.6 B.9
C.12 D.15
【解析】选C.∵四边形ABCD是平行四边形.
∴∠DAB=∠DCB,AB∥CD,AB=CD,AD∥BC,AD=BC,
又∵AC平分∠DAB,∴∠DAC=∠BAC
∴∠DAC=∠DCA,∴AD=DC.又∵AB=3,
∴□ABCD的周长为AB+BC+CD+DA=4AB=12.5.(苏州?中考)如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.【解析】∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
又E是AD边上的中点,
∴AD=2AE=4,
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:126.如图,在平面直角坐标系中,□OBCD的顶点O,B,D的坐标如图所示,则顶点C的坐标为( )xyCO (0,0)B(5,0)D(2,3)A. (3,7) B. (5,3) C. (7,3) D. (8,2)C1、如图,在若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______A:基础知识:B:变式训练:若∠A+ ∠C= 200°,则∠A=______ 、∠B=______50°130° 50°100°80°返回角的运算2.如图,在□ ABCD中, ∠B=110°,延长AD至F,延长CD至E,连结EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
【解析】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.3.(2013·黔西南中考)已知□ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
【解析】选C.∵∠A+∠C=200°,∠A=∠C,∴∠A=100°.又∵AD∥BC,∴∠A+∠B=180°,∴∠B=80°.4.(2012·成都中考)将□ABCD的一边BC延
长至E,若∠A=110°,则∠1= .
【解析】在□ABCD中,∠BCD=∠A=110°,∴∠1=180°-∠BCD=70°.
答案:70°1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ ABCD的面积. 对角线相关的运算2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8DODBAC3.如图,在□ABCD中, 对角线AC,BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.54.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,
BD=8,则AD的取值范围是 __. 1<AD<95.如图,□ ABCD中,AE⊥BD,∠EAD=60°,AE=2 cm,AC+BD=14 cm,则△OBC的周长是____cm.
【解析】在□ABCD中,BC=AD,OA=OC,OB=OD,
∵AE⊥BD,∠EAD=60°,AE=2 cm,∴AD=4 cm,BC=4cm,
∵AC+BD=14 cm,
∴OB+OC=7 cm,
∴△OBC的周长=OB+OC+BC=11 cm.
答案:116.平行四边形ABCD的两条对角线相交于O,OA,OB,AB的长度分别为3 cm,4 cm,5 cm,求其他各边以及两条对角线的长度.【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
OA=OC,OB=OD.
又∵OA=3 cm,OB=4 cm,AB=5 cm,
∴AC=6 cm,BD=8 cm,CD=5 cm.
∵△AOB中,32+42=52,即AO2+BO2=AB2,
∴∠AOB=90°,∴AC⊥BD,
∴Rt△AOD中,OA2+OD2=AD2,
∴AD=5 cm,BC=5 cm.
答:这个平行四边形的其他各边长都是5 cm,两条对角线长分别为6 cm和8 cm.1.如图,□ ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6
C.12 D.24
【解析】选C.观察图形会发现,每一小块阴影三角形都
与它相对的三角形全等,则阴影部分的面积等于平行四
边形面积的一半.故S阴影= = ×6×4=12.对称性相关的运算
记作: ABCD
读作:平行四边形ABCD
2.平行四边形相对的边称为 对边, 相邻的边称为邻边;相对的角称为对角.相邻的角称为邻角.3.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.平行四边形相关概念平行四边形的性质性质1两组对边分别平行在平行四边形ABCD中
AB∥CD,AD∥BC。性质2两组对边分别相等已知:平行四边形ABCD;
求证:AB=CD,AD=BC。证明:连接AC。
∵ABCD是平行四边形(已知)
∴AB∥CD,AD∥BC(性质1)
∴∠BAC=∠DCA,∠ACB=∠CAD(两直线平行,内错角相等)在△ABC和△ADC中
∵ ∠BAC=∠DCA,AC=CA,∠ACB=∠CAD
∴ △ABC≌ △ADC(ASA)
∴AB=CD,AD=BC(全等三角形对应边相等)性质3两组对角分别相等已知:平行四边形ABCD;
求证: ∠A= ∠C, ∠B= ∠D。证明:∵ABCD是平行四边形(已知)
∴AB∥CD,AD∥BC(性质1)
∴∠A+∠D=180°, ∠A+∠B=180°(两直线平行,同旁内角互补)
∴ ∠B= ∠D(同角的补角相等)
同理可证∠A= ∠C性质4对角线互相平分已知:平行四边形ABCD,对角线AC和BD交于点E;
求证AE=EC,BE=ED。证明:∵ABCD是平行四边形(已知)
∴AD=BC(性质2)
AD∥BC(性质1)
∴∠ADB=∠CBD,∠ACB=∠CAD(两直线平行,内错角相等)
在△ADE和△CBE中
∵ ∠ADB=∠CBD,AD=CB,∠CAD=∠ACB,
∴ △ADE≌ △CBE(ASA)
∴AE=EC,BE=ED(全等三角形对应边相等)性质5是中心对称图形已知:平行四边形ABCD;
求证:ABCD是中心对称图形。证明:∵ABCD是平行四边形(已知)
∴AE=EC,BE=ED(性质4)
∴A与C关于E成中心对称,B与D关于E成中心对称(中心对称的性质)
∴平行四边形ABCD关于E成中心对称。
平行四边形的性质几何语言:两组对边分别平行且相等∵ 四边形ABCD是平行四边形∴ AB∥CD,AD∥BC. (平行四边形的对边平行)
AB=CD, AD=BC (平行四边形的对边相等)∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) AE= EC, BE= ED(平行四边形的对角线互相平分) 两组对角分别相等对角线互相平分是中心对称图形例题解析例1、在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别是E和F,求证:AE=CF证明:∵ 四边形ABCD是平行四边形
∴AD=BC,∠A= ∠C∵ DE⊥AB,BF⊥CD
∴∠AED= ∠CFB
在△ADE和△CBF中∠A=∠C
∠AED=∠CFB
AD=BC∴ △ADE≌△CBF(AAS)∴ AE=CF平行线间的距离处处相等1、如图在A基础知识:(1)若AB=1㎝,BC=2 ㎝B变式训练:(2)若AB:BC=3:4,周长为14㎝,则CD=——,DA=——(1)若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____6cm5cm3cm4cm8cm28cm边的运算A.6cm B.12cm C.4cm D.8cmABDC2.如图, □ABCD的周长是28cm,△ABC的周长是22cm,则
AC的长为( )D3.(广州·中考)已知□ABCD的周长为32,AB=4,则BC=( )
A. 4 B. 12 C. 24 D. 28【解析】选B.根据平行四边形的性质可以得出AB=CD,BC=AD,又因AB+CD+BC+AD=32,所以BC=12.4.(河北?中考)如图,在□ ABCD中,AC平分
∠DAB,AB=3,则□ ABCD的周长为( )
A.6 B.9
C.12 D.15
【解析】选C.∵四边形ABCD是平行四边形.
∴∠DAB=∠DCB,AB∥CD,AB=CD,AD∥BC,AD=BC,
又∵AC平分∠DAB,∴∠DAC=∠BAC
∴∠DAC=∠DCA,∴AD=DC.又∵AB=3,
∴□ABCD的周长为AB+BC+CD+DA=4AB=12.5.(苏州?中考)如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是______.【解析】∵四边形ABCD是平行四边形,
∴AD BC,AB DC.
∵∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
又E是AD边上的中点,
∴AD=2AE=4,
∴平行四边形ABCD的周长为AB+BC+CD+AD=2+4+2+4=12.
答案:126.如图,在平面直角坐标系中,□OBCD的顶点O,B,D的坐标如图所示,则顶点C的坐标为( )xyCO (0,0)B(5,0)D(2,3)A. (3,7) B. (5,3) C. (7,3) D. (8,2)C1、如图,在若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______A:基础知识:B:变式训练:若∠A+ ∠C= 200°,则∠A=______ 、∠B=______50°130° 50°100°80°返回角的运算2.如图,在□ ABCD中, ∠B=110°,延长AD至F,延长CD至E,连结EF,则∠E+∠F的值为( )
A.110° B.30° C.50° D.70°
【解析】选D.在□ABCD中,∠B=110°,∴∠ADC=∠B=110°,∴∠CDF=70°,由三角形外角的性质得,∠E+∠F=70°.3.(2013·黔西南中考)已知□ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
【解析】选C.∵∠A+∠C=200°,∠A=∠C,∴∠A=100°.又∵AD∥BC,∴∠A+∠B=180°,∴∠B=80°.4.(2012·成都中考)将□ABCD的一边BC延
长至E,若∠A=110°,则∠1= .
【解析】在□ABCD中,∠BCD=∠A=110°,∴∠1=180°-∠BCD=70°.
答案:70°1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ ABCD的面积. 对角线相关的运算2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8DODBAC3.如图,在□ABCD中, 对角线AC,BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.54.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,
BD=8,则AD的取值范围是 __. 1<AD<95.如图,□ ABCD中,AE⊥BD,∠EAD=60°,AE=2 cm,AC+BD=14 cm,则△OBC的周长是____cm.
【解析】在□ABCD中,BC=AD,OA=OC,OB=OD,
∵AE⊥BD,∠EAD=60°,AE=2 cm,∴AD=4 cm,BC=4cm,
∵AC+BD=14 cm,
∴OB+OC=7 cm,
∴△OBC的周长=OB+OC+BC=11 cm.
答案:116.平行四边形ABCD的两条对角线相交于O,OA,OB,AB的长度分别为3 cm,4 cm,5 cm,求其他各边以及两条对角线的长度.【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
OA=OC,OB=OD.
又∵OA=3 cm,OB=4 cm,AB=5 cm,
∴AC=6 cm,BD=8 cm,CD=5 cm.
∵△AOB中,32+42=52,即AO2+BO2=AB2,
∴∠AOB=90°,∴AC⊥BD,
∴Rt△AOD中,OA2+OD2=AD2,
∴AD=5 cm,BC=5 cm.
答:这个平行四边形的其他各边长都是5 cm,两条对角线长分别为6 cm和8 cm.1.如图,□ ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6
C.12 D.24
【解析】选C.观察图形会发现,每一小块阴影三角形都
与它相对的三角形全等,则阴影部分的面积等于平行四
边形面积的一半.故S阴影= = ×6×4=12.对称性相关的运算
