7.4 平行线的判定 课件(共25张PPT)
文档属性
| 名称 | 7.4 平行线的判定 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 12:20:07 | ||
图片预览








文档简介
(共25张PPT)
冀教版2024教材数学七年级下册
7.4 平行线的判定
授课教师:********
班 级:********
时 间:********
第七章 相交线与平行线
学习目标
1.探索平行线的判定定理“内错角相等,两直线平行”“ 同旁内角互补,两直线平行”.
2.会合理选用平行线的判定方法判定两条直线平行.
3.进一步感受说理的表达方式,体会“推理"的意义和作用.
我将为你设计一份详细的二元一次方程组教案,重点突出概念讲解、解法推导及实际应用,帮助学生深入理解和掌握相关知识。
# 二元一次方程组教案
## 一、教学目标
1. 知识与技能目标
- 理解二元一次方程、二元一次方程组及其解的概念。
- 熟练掌握用代入消元法和加减消元法解二元一次方程组。
- 能根据实际问题列出二元一次方程组并求解,体会方程组是刻画现实世界中含有两个未知数的问题的有效数学模型。
2. 过程与方法目标
- 通过对实际问题的分析,经历从实际问题中抽象出数学模型的过程,提高分析问题和解决问题的能力。
- 在探索二元一次方程组解法的过程中,体会消元思想,培养学生的化归意识和运算能力。
3. 情感态度与价值观目标
- 感受数学与生活的紧密联系,激发学生学习数学的兴趣。
- 在合作交流中,培养学生的团队合作精神和创新意识。
## 二、教学重难点
1. **教学重点**
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组。
- 用二元一次方程组解决实际问题。
2. **教学难点**
- 理解消元思想,掌握消元的方法将二元一次方程组转化为一元一次方程。
- 从实际问题中找出等量关系,列出二元一次方程组。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
### (一)导入新课(5分钟)
1. 展示问题情境:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
2. 引导学生思考:
- 你能根据问题中的等量关系列出方程吗?
- 如果设两个未知数,如何表示这些等量关系?
### (二)讲授新课(30分钟)
1. **二元一次方程的概念**
- 引导学生设胜x场,负y场,根据等量关系列出方程:x + y = 10,2x + y = 16。
- 观察这两个方程的特点,总结二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。
- 举例让学生判断哪些是二元一次方程,如3x - 2y = 5,xy = 1等,加深对概念的理解。
2. **二元一次方程组的概念**
- 像这样把两个二元一次方程合在一起,就组成了一个二元一次方程组。
- 强调二元一次方程组中两个方程共含有两个相同的未知数。
3. **二元一次方程组的解**
- 让学生尝试找出满足方程组x + y = 10,2x + y = 16的x和y的值。
- 给出二元一次方程组的解的定义:一般地,使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
- 通过具体例子,让学生理解方程组的解是一对数,并且要同时满足方程组中的两个方程。
4. **代入消元法解二元一次方程组**
- 以方程组x + y = 10,2x + y = 16为例,讲解代入消元法。
- 分析:由方程x + y = 10可得y = 10 - x,将其代入方程2x + y = 16中,就可以消去y,得到一个关于x的一元一次方程。
- 详细讲解解题步骤:
- 由方程①得:y = 10 - x ③
- 把③代入②得:2x + (10 - x) = 16
- 解这个方程:2x + 10 - x = 16,x = 6
- 把x = 6代入③得:y = 10 - 6 = 4
- 所以方程组的解为x = 6,y = 4
- 总结代入消元法的步骤:
- 变形:从方程组中选一个系数比较简单的方程,将这个方程中的一个未知数用含另一个未知数的代数式表示出来。
- 代入:将变形后的式子代入另一个方程,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入变形后的式子,求出另一个未知数的值。
- 写解:写出方程组的解。
5. **加减消元法解二元一次方程组**
- 给出方程组2x + 3y = 11,2x - 5y = -1,引导学生观察两个方程中x的系数相同。
- 讲解:可以将两个方程相减,消去x,得到关于y的一元一次方程。
- 具体步骤:
- 用方程① - ②得:(2x + 3y) - (2x - 5y) = 11 - (-1)
- 去括号得:2x + 3y - 2x + 5y = 11 + 1
- 合并同类项得:8y = 12
- 解得:y = 1.5
- 把y = 1.5代入①得:2x + 3×1.5 = 11
- 解这个方程得:2x = 11 - 4.5,2x = 6.5,x = 3.25
- 所以方程组的解为x = 3.25,y = 1.5
- 总结加减消元法的步骤:
- 观察:观察方程组中两个方程相同未知数的系数特点。
- 变形:如果相同未知数的系数相等或互为相反数,则直接进行加减消元;如果系数不相等也不互为相反数,通过乘以适当的数,使某个未知数的系数相等或互为相反数。
- 加减:将两个方程相加或相减,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入原方程组中的一个方程,求出另一个未知数的值。
- 写解:写出方程组的解。
### (三)课堂练习(15分钟)
1. 给出一些二元一次方程、二元一次方程组,让学生判断并说明理由。
2. 用代入消元法和加减消元法解简单的二元一次方程组,如x - y = 3,3x - 8y = 14等,找学生板演,教师巡视指导,及时纠正学生的错误。
3. 出示一道实际问题:某班去看演出,甲种票每张24元,乙种票每张18元。如果35名学生购票恰好用去750元,甲乙两种票各买了多少张?引导学生分析问题,找出等量关系,列出二元一次方程组并求解。
### (四)课堂小结(5分钟)
1. 与学生一起回顾本节课所学内容:
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组的步骤和方法。
- 用二元一次方程组解决实际问题的一般步骤。
2. 强调重点和难点,鼓励学生在课后多做练习,巩固所学知识。
### (五)布置作业(5分钟)
1. 基础作业:课本课后练习题,用代入消元法和加减消元法解给定的二元一次方程组。
2. 拓展作业:寻找生活中的实际问题,用二元一次方程组来解决,并写成小报告形式。
## 五、教学反思
在本节课的教学过程中,要注重引导学生从实际问题出发,逐步理解二元一次方程组的相关概念和解法。在讲解代入消元法和加减消元法时,要让学生充分理解消元的思想,通过大量的练习让学生熟练掌握两种解法。同时,在解决实际问题时,要培养学生分析问题、找出等量关系的能力。在教学过程中,要关注学生的反应,及时调整教学节奏和方法,确保学生能够理解和掌握所学内容。
这份教案从导入到作业布置,涵盖教学各环节。你看看是否符合你的教学需求,若有调整方向,如增减某部分内容,可随时告诉我。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
问题 前面你学了平行线的哪些判定方法?
同位角相等,两直线平行.
思考 还有其他判定两条直线平行的方法吗?
如图,直线AB,CD与直线EF相交,若∠2=∠3,试判断直线AB,CD的位置关系.
A
B
C
D
E
F
1
2
3
4
还有没有别的办法判定直线AB与CD的位置关系呢?
∵∠2=∠3,
∴AB∥CD(同位角相等,两直线平行).
∵∠1=∠3(对顶角相等),如果∠1=∠2,那么就能推出∠2=∠3,于是就有AB∥CD.
他们的想法正确吗?
知识点 平行线的判定定理
∵∠3+∠4=180°(平角的定义),
如果∠2+∠4=180°,
那么就能推出∠2=∠3,
于是就有AB∥CD.
命题1 如图,已知直线AB,CD被直线EF所截,
∠1=∠2,那么AB∥CD.
理由:
∵∠1=∠2( ),
∠1=∠3( ),
∴ ∠2=∠3( ).
∴ AB∥CD ( ).
已知
对顶角相等
等量代换
同位角相等,两直线平行
通过命题1,我们能得到什么结论?
知识点 平行线的判定定理
A
B
C
D
E
F
1
2
3
4
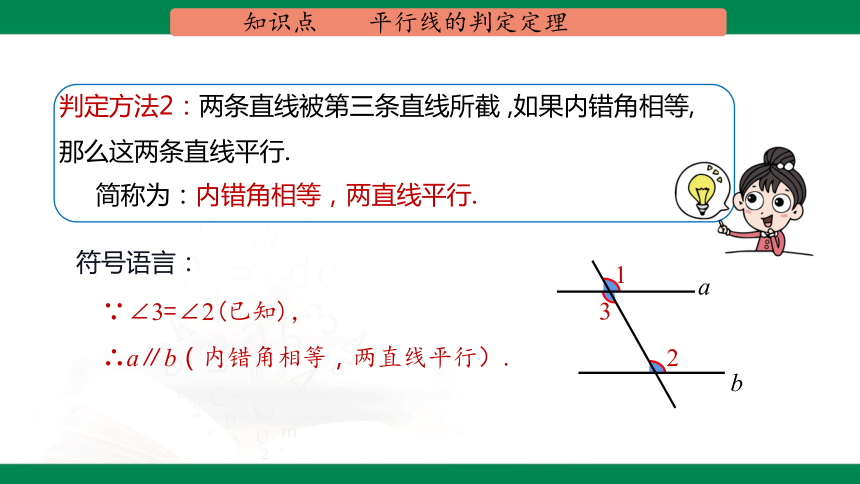
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简称为:内错角相等,两直线平行.
2
b
a
1
3
∵∠3=∠2(已知),
∴a∥b(内错角相等,两直线平行).
符号语言:
知识点 平行线的判定定理
命题2 如图,已知直线AB,CD被直线EF所截,
∠2+∠4=180°,那么AB∥CD.
理由:
∵∠2+∠4=180°( ),
∠3+∠4=180°( ),
∴ ∠2=180°-∠4,∠3=180°-∠4
( ).
∴ AB∥CD ( ).
已知
平角定义
同位角相等,两直线平行
等式的基本性质
∴ ∠2=∠3( ),
等量代换
通过命题2,我们能得到什么结论?
知识点 平行线的判定定理
A
B
C
D
E
F
1
2
3
4
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简称为:同旁内角互补,两直线平行.
符号语言:
2
b
a
1
3
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
知识点 平行线的判定定理
例1 如图,下列条件能判定直线l1//l2的是( )
A. ∠1=∠2 B. ∠1+∠3=180°
C. ∠4=∠5 D. ∠3=∠5
B
知识点 平行线的判定定理
例2 如图,已知直线AB,CD被直线EF所截,∠1=60°,∠2=120°.请说明AB∥CD的理由.
A
B
C
D
E
F
1
2
3
4
理由:∵∠1=60°,∠2=120°(已知)
∴∠1+∠2=60°+120°=180°.
∵∠2=∠4 (对顶角相等),
∴ ∠1+∠4=180°(等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
知识点 平行线的判定定理
1. [2024唐山期末] 如图,在下列条件中,能判定 的
是( )
A
A. B.
C. D.
返回
2. [2024石家庄校级月考] 在下列图形中,已知 ,一
定能推导出 的是( )
D
A. B. C. D.
返回
3. 如图,点在 的延长线上,在不
增加辅助线的前提下,增加一个条件____________________
_______后,能判定 .
(答案不唯一)
(第3题)
返回
4.[2024廊坊期末] 如图,下列条件:
(第4题)
; ;
; .
其中,能得到直线 的有___个.
3
返回
5.如图,将三个相同的三角板不重叠、不留空隙地拼在一起,
观察图形,在线段,,,,, 中,相互平
行的线段有___组.
3
(第5题)
返回
(第6题)
6. 如图,一个弯形管道的
拐角 ,若工人师傅准备在点
处对管道进行加工(拐弯),要保证拐弯后
与平行,则拐角 的度数是_____
_______.
或
【点拨】过点作 .如图①,
, ,
;
如图②, , ,
.综上,加工
后拐角的度数是 或 .
返回
7.如图, ,
,与
平行吗?为什么?
【解】 ,
.
,.
, .
返回
8. 下列各图中,能画出 的是( )
D
A. ①②③ B. ①②④ C. ③④ D. ①②③④
返回
9. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍按原来的
方向前进,那么两次拐弯的角度是( )
B
A. 第一次右拐 ,第二次左拐
B. 第一次左拐 ,第二次右拐
C. 第一次左拐 ,第二次左拐
D. 第一次右拐 ,第二次右拐
返回
10. 下面是验证
纸条两条边, 是否平行的
不同折叠方式:
(1)如图①,展开后测得 ;
(2)如图②,测得 ;
(3)如图③,展开后测得 ;
(4)如图④,展开后测得 .
其中能判定 的是__________(填序号).
返回
判定两条直线平行的方法
文字叙述 符号语言 图形
相等 两直线平行
相等 两直线平行 互补,两直线平行 同位角
内错角
同旁内角
∵∠1=∠2(已知),
∴a∥b.
a
b
c
1
2
3
4
∵∠3=∠2(已知),
∴a∥b.
∵∠4+∠2=180°(已知),∴a∥b.
谢谢观看!
冀教版2024教材数学七年级下册
7.4 平行线的判定
授课教师:********
班 级:********
时 间:********
第七章 相交线与平行线
学习目标
1.探索平行线的判定定理“内错角相等,两直线平行”“ 同旁内角互补,两直线平行”.
2.会合理选用平行线的判定方法判定两条直线平行.
3.进一步感受说理的表达方式,体会“推理"的意义和作用.
我将为你设计一份详细的二元一次方程组教案,重点突出概念讲解、解法推导及实际应用,帮助学生深入理解和掌握相关知识。
# 二元一次方程组教案
## 一、教学目标
1. 知识与技能目标
- 理解二元一次方程、二元一次方程组及其解的概念。
- 熟练掌握用代入消元法和加减消元法解二元一次方程组。
- 能根据实际问题列出二元一次方程组并求解,体会方程组是刻画现实世界中含有两个未知数的问题的有效数学模型。
2. 过程与方法目标
- 通过对实际问题的分析,经历从实际问题中抽象出数学模型的过程,提高分析问题和解决问题的能力。
- 在探索二元一次方程组解法的过程中,体会消元思想,培养学生的化归意识和运算能力。
3. 情感态度与价值观目标
- 感受数学与生活的紧密联系,激发学生学习数学的兴趣。
- 在合作交流中,培养学生的团队合作精神和创新意识。
## 二、教学重难点
1. **教学重点**
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组。
- 用二元一次方程组解决实际问题。
2. **教学难点**
- 理解消元思想,掌握消元的方法将二元一次方程组转化为一元一次方程。
- 从实际问题中找出等量关系,列出二元一次方程组。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
### (一)导入新课(5分钟)
1. 展示问题情境:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
2. 引导学生思考:
- 你能根据问题中的等量关系列出方程吗?
- 如果设两个未知数,如何表示这些等量关系?
### (二)讲授新课(30分钟)
1. **二元一次方程的概念**
- 引导学生设胜x场,负y场,根据等量关系列出方程:x + y = 10,2x + y = 16。
- 观察这两个方程的特点,总结二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。
- 举例让学生判断哪些是二元一次方程,如3x - 2y = 5,xy = 1等,加深对概念的理解。
2. **二元一次方程组的概念**
- 像这样把两个二元一次方程合在一起,就组成了一个二元一次方程组。
- 强调二元一次方程组中两个方程共含有两个相同的未知数。
3. **二元一次方程组的解**
- 让学生尝试找出满足方程组x + y = 10,2x + y = 16的x和y的值。
- 给出二元一次方程组的解的定义:一般地,使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
- 通过具体例子,让学生理解方程组的解是一对数,并且要同时满足方程组中的两个方程。
4. **代入消元法解二元一次方程组**
- 以方程组x + y = 10,2x + y = 16为例,讲解代入消元法。
- 分析:由方程x + y = 10可得y = 10 - x,将其代入方程2x + y = 16中,就可以消去y,得到一个关于x的一元一次方程。
- 详细讲解解题步骤:
- 由方程①得:y = 10 - x ③
- 把③代入②得:2x + (10 - x) = 16
- 解这个方程:2x + 10 - x = 16,x = 6
- 把x = 6代入③得:y = 10 - 6 = 4
- 所以方程组的解为x = 6,y = 4
- 总结代入消元法的步骤:
- 变形:从方程组中选一个系数比较简单的方程,将这个方程中的一个未知数用含另一个未知数的代数式表示出来。
- 代入:将变形后的式子代入另一个方程,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入变形后的式子,求出另一个未知数的值。
- 写解:写出方程组的解。
5. **加减消元法解二元一次方程组**
- 给出方程组2x + 3y = 11,2x - 5y = -1,引导学生观察两个方程中x的系数相同。
- 讲解:可以将两个方程相减,消去x,得到关于y的一元一次方程。
- 具体步骤:
- 用方程① - ②得:(2x + 3y) - (2x - 5y) = 11 - (-1)
- 去括号得:2x + 3y - 2x + 5y = 11 + 1
- 合并同类项得:8y = 12
- 解得:y = 1.5
- 把y = 1.5代入①得:2x + 3×1.5 = 11
- 解这个方程得:2x = 11 - 4.5,2x = 6.5,x = 3.25
- 所以方程组的解为x = 3.25,y = 1.5
- 总结加减消元法的步骤:
- 观察:观察方程组中两个方程相同未知数的系数特点。
- 变形:如果相同未知数的系数相等或互为相反数,则直接进行加减消元;如果系数不相等也不互为相反数,通过乘以适当的数,使某个未知数的系数相等或互为相反数。
- 加减:将两个方程相加或相减,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入原方程组中的一个方程,求出另一个未知数的值。
- 写解:写出方程组的解。
### (三)课堂练习(15分钟)
1. 给出一些二元一次方程、二元一次方程组,让学生判断并说明理由。
2. 用代入消元法和加减消元法解简单的二元一次方程组,如x - y = 3,3x - 8y = 14等,找学生板演,教师巡视指导,及时纠正学生的错误。
3. 出示一道实际问题:某班去看演出,甲种票每张24元,乙种票每张18元。如果35名学生购票恰好用去750元,甲乙两种票各买了多少张?引导学生分析问题,找出等量关系,列出二元一次方程组并求解。
### (四)课堂小结(5分钟)
1. 与学生一起回顾本节课所学内容:
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组的步骤和方法。
- 用二元一次方程组解决实际问题的一般步骤。
2. 强调重点和难点,鼓励学生在课后多做练习,巩固所学知识。
### (五)布置作业(5分钟)
1. 基础作业:课本课后练习题,用代入消元法和加减消元法解给定的二元一次方程组。
2. 拓展作业:寻找生活中的实际问题,用二元一次方程组来解决,并写成小报告形式。
## 五、教学反思
在本节课的教学过程中,要注重引导学生从实际问题出发,逐步理解二元一次方程组的相关概念和解法。在讲解代入消元法和加减消元法时,要让学生充分理解消元的思想,通过大量的练习让学生熟练掌握两种解法。同时,在解决实际问题时,要培养学生分析问题、找出等量关系的能力。在教学过程中,要关注学生的反应,及时调整教学节奏和方法,确保学生能够理解和掌握所学内容。
这份教案从导入到作业布置,涵盖教学各环节。你看看是否符合你的教学需求,若有调整方向,如增减某部分内容,可随时告诉我。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
问题 前面你学了平行线的哪些判定方法?
同位角相等,两直线平行.
思考 还有其他判定两条直线平行的方法吗?
如图,直线AB,CD与直线EF相交,若∠2=∠3,试判断直线AB,CD的位置关系.
A
B
C
D
E
F
1
2
3
4
还有没有别的办法判定直线AB与CD的位置关系呢?
∵∠2=∠3,
∴AB∥CD(同位角相等,两直线平行).
∵∠1=∠3(对顶角相等),如果∠1=∠2,那么就能推出∠2=∠3,于是就有AB∥CD.
他们的想法正确吗?
知识点 平行线的判定定理
∵∠3+∠4=180°(平角的定义),
如果∠2+∠4=180°,
那么就能推出∠2=∠3,
于是就有AB∥CD.
命题1 如图,已知直线AB,CD被直线EF所截,
∠1=∠2,那么AB∥CD.
理由:
∵∠1=∠2( ),
∠1=∠3( ),
∴ ∠2=∠3( ).
∴ AB∥CD ( ).
已知
对顶角相等
等量代换
同位角相等,两直线平行
通过命题1,我们能得到什么结论?
知识点 平行线的判定定理
A
B
C
D
E
F
1
2
3
4
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简称为:内错角相等,两直线平行.
2
b
a
1
3
∵∠3=∠2(已知),
∴a∥b(内错角相等,两直线平行).
符号语言:
知识点 平行线的判定定理
命题2 如图,已知直线AB,CD被直线EF所截,
∠2+∠4=180°,那么AB∥CD.
理由:
∵∠2+∠4=180°( ),
∠3+∠4=180°( ),
∴ ∠2=180°-∠4,∠3=180°-∠4
( ).
∴ AB∥CD ( ).
已知
平角定义
同位角相等,两直线平行
等式的基本性质
∴ ∠2=∠3( ),
等量代换
通过命题2,我们能得到什么结论?
知识点 平行线的判定定理
A
B
C
D
E
F
1
2
3
4
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简称为:同旁内角互补,两直线平行.
符号语言:
2
b
a
1
3
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
知识点 平行线的判定定理
例1 如图,下列条件能判定直线l1//l2的是( )
A. ∠1=∠2 B. ∠1+∠3=180°
C. ∠4=∠5 D. ∠3=∠5
B
知识点 平行线的判定定理
例2 如图,已知直线AB,CD被直线EF所截,∠1=60°,∠2=120°.请说明AB∥CD的理由.
A
B
C
D
E
F
1
2
3
4
理由:∵∠1=60°,∠2=120°(已知)
∴∠1+∠2=60°+120°=180°.
∵∠2=∠4 (对顶角相等),
∴ ∠1+∠4=180°(等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
知识点 平行线的判定定理
1. [2024唐山期末] 如图,在下列条件中,能判定 的
是( )
A
A. B.
C. D.
返回
2. [2024石家庄校级月考] 在下列图形中,已知 ,一
定能推导出 的是( )
D
A. B. C. D.
返回
3. 如图,点在 的延长线上,在不
增加辅助线的前提下,增加一个条件____________________
_______后,能判定 .
(答案不唯一)
(第3题)
返回
4.[2024廊坊期末] 如图,下列条件:
(第4题)
; ;
; .
其中,能得到直线 的有___个.
3
返回
5.如图,将三个相同的三角板不重叠、不留空隙地拼在一起,
观察图形,在线段,,,,, 中,相互平
行的线段有___组.
3
(第5题)
返回
(第6题)
6. 如图,一个弯形管道的
拐角 ,若工人师傅准备在点
处对管道进行加工(拐弯),要保证拐弯后
与平行,则拐角 的度数是_____
_______.
或
【点拨】过点作 .如图①,
, ,
;
如图②, , ,
.综上,加工
后拐角的度数是 或 .
返回
7.如图, ,
,与
平行吗?为什么?
【解】 ,
.
,.
, .
返回
8. 下列各图中,能画出 的是( )
D
A. ①②③ B. ①②④ C. ③④ D. ①②③④
返回
9. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍按原来的
方向前进,那么两次拐弯的角度是( )
B
A. 第一次右拐 ,第二次左拐
B. 第一次左拐 ,第二次右拐
C. 第一次左拐 ,第二次左拐
D. 第一次右拐 ,第二次右拐
返回
10. 下面是验证
纸条两条边, 是否平行的
不同折叠方式:
(1)如图①,展开后测得 ;
(2)如图②,测得 ;
(3)如图③,展开后测得 ;
(4)如图④,展开后测得 .
其中能判定 的是__________(填序号).
返回
判定两条直线平行的方法
文字叙述 符号语言 图形
相等 两直线平行
相等 两直线平行 互补,两直线平行 同位角
内错角
同旁内角
∵∠1=∠2(已知),
∴a∥b.
a
b
c
1
2
3
4
∵∠3=∠2(已知),
∴a∥b.
∵∠4+∠2=180°(已知),∴a∥b.
谢谢观看!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
