8.6 科学记数法 课件(共29张PPT)
文档属性
| 名称 | 8.6 科学记数法 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
冀教版2024教材数学七年级下册
8.6 科学记数法
授课教师:********
班 级:********
时 间:********
第八章 整式的乘法
学习目标
1.会用科学记数法表示小于1的正数.
2.能将科学记数法表示的数还原成原数.
我将为你设计一份详细的二元一次方程组教案,重点突出概念讲解、解法推导及实际应用,帮助学生深入理解和掌握相关知识。
# 二元一次方程组教案
## 一、教学目标
1. 知识与技能目标
- 理解二元一次方程、二元一次方程组及其解的概念。
- 熟练掌握用代入消元法和加减消元法解二元一次方程组。
- 能根据实际问题列出二元一次方程组并求解,体会方程组是刻画现实世界中含有两个未知数的问题的有效数学模型。
2. 过程与方法目标
- 通过对实际问题的分析,经历从实际问题中抽象出数学模型的过程,提高分析问题和解决问题的能力。
- 在探索二元一次方程组解法的过程中,体会消元思想,培养学生的化归意识和运算能力。
3. 情感态度与价值观目标
- 感受数学与生活的紧密联系,激发学生学习数学的兴趣。
- 在合作交流中,培养学生的团队合作精神和创新意识。
## 二、教学重难点
1. **教学重点**
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组。
- 用二元一次方程组解决实际问题。
2. **教学难点**
- 理解消元思想,掌握消元的方法将二元一次方程组转化为一元一次方程。
- 从实际问题中找出等量关系,列出二元一次方程组。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
### (一)导入新课(5分钟)
1. 展示问题情境:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
2. 引导学生思考:
- 你能根据问题中的等量关系列出方程吗?
- 如果设两个未知数,如何表示这些等量关系?
### (二)讲授新课(30分钟)
1. **二元一次方程的概念**
- 引导学生设胜x场,负y场,根据等量关系列出方程:x + y = 10,2x + y = 16。
- 观察这两个方程的特点,总结二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。
- 举例让学生判断哪些是二元一次方程,如3x - 2y = 5,xy = 1等,加深对概念的理解。
2. **二元一次方程组的概念**
- 像这样把两个二元一次方程合在一起,就组成了一个二元一次方程组。
- 强调二元一次方程组中两个方程共含有两个相同的未知数。
3. **二元一次方程组的解**
- 让学生尝试找出满足方程组x + y = 10,2x + y = 16的x和y的值。
- 给出二元一次方程组的解的定义:一般地,使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
- 通过具体例子,让学生理解方程组的解是一对数,并且要同时满足方程组中的两个方程。
4. **代入消元法解二元一次方程组**
- 以方程组x + y = 10,2x + y = 16为例,讲解代入消元法。
- 分析:由方程x + y = 10可得y = 10 - x,将其代入方程2x + y = 16中,就可以消去y,得到一个关于x的一元一次方程。
- 详细讲解解题步骤:
- 由方程①得:y = 10 - x ③
- 把③代入②得:2x + (10 - x) = 16
- 解这个方程:2x + 10 - x = 16,x = 6
- 把x = 6代入③得:y = 10 - 6 = 4
- 所以方程组的解为x = 6,y = 4
- 总结代入消元法的步骤:
- 变形:从方程组中选一个系数比较简单的方程,将这个方程中的一个未知数用含另一个未知数的代数式表示出来。
- 代入:将变形后的式子代入另一个方程,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入变形后的式子,求出另一个未知数的值。
- 写解:写出方程组的解。
5. **加减消元法解二元一次方程组**
- 给出方程组2x + 3y = 11,2x - 5y = -1,引导学生观察两个方程中x的系数相同。
- 讲解:可以将两个方程相减,消去x,得到关于y的一元一次方程。
- 具体步骤:
- 用方程① - ②得:(2x + 3y) - (2x - 5y) = 11 - (-1)
- 去括号得:2x + 3y - 2x + 5y = 11 + 1
- 合并同类项得:8y = 12
- 解得:y = 1.5
- 把y = 1.5代入①得:2x + 3×1.5 = 11
- 解这个方程得:2x = 11 - 4.5,2x = 6.5,x = 3.25
- 所以方程组的解为x = 3.25,y = 1.5
- 总结加减消元法的步骤:
- 观察:观察方程组中两个方程相同未知数的系数特点。
- 变形:如果相同未知数的系数相等或互为相反数,则直接进行加减消元;如果系数不相等也不互为相反数,通过乘以适当的数,使某个未知数的系数相等或互为相反数。
- 加减:将两个方程相加或相减,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入原方程组中的一个方程,求出另一个未知数的值。
- 写解:写出方程组的解。
### (三)课堂练习(15分钟)
1. 给出一些二元一次方程、二元一次方程组,让学生判断并说明理由。
2. 用代入消元法和加减消元法解简单的二元一次方程组,如x - y = 3,3x - 8y = 14等,找学生板演,教师巡视指导,及时纠正学生的错误。
3. 出示一道实际问题:某班去看演出,甲种票每张24元,乙种票每张18元。如果35名学生购票恰好用去750元,甲乙两种票各买了多少张?引导学生分析问题,找出等量关系,列出二元一次方程组并求解。
### (四)课堂小结(5分钟)
1. 与学生一起回顾本节课所学内容:
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组的步骤和方法。
- 用二元一次方程组解决实际问题的一般步骤。
2. 强调重点和难点,鼓励学生在课后多做练习,巩固所学知识。
### (五)布置作业(5分钟)
1. 基础作业:课本课后练习题,用代入消元法和加减消元法解给定的二元一次方程组。
2. 拓展作业:寻找生活中的实际问题,用二元一次方程组来解决,并写成小报告形式。
## 五、教学反思
在本节课的教学过程中,要注重引导学生从实际问题出发,逐步理解二元一次方程组的相关概念和解法。在讲解代入消元法和加减消元法时,要让学生充分理解消元的思想,通过大量的练习让学生熟练掌握两种解法。同时,在解决实际问题时,要培养学生分析问题、找出等量关系的能力。在教学过程中,要关注学生的反应,及时调整教学节奏和方法,确保学生能够理解和掌握所学内容。
这份教案从导入到作业布置,涵盖教学各环节。你看看是否符合你的教学需求,若有调整方向,如增减某部分内容,可随时告诉我。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
1000=
1000 000=
1000 000 000=
1000 000 000 000=
103
106
109
1012
100 …… 00
n个0
=10n
思考:如果1个1后边有n个0,这样的数可以简记作什么?
记作:10n
观察
光速300 000 000米/秒
太阳半径约696 000千米
PM2.5是指大气中直径小于或等于0.000 0025 m的颗粒物
人体红细胞的平均直径为0.000 007 7m
(1)第六次人口普查时,中国人口约为1370000000人;
(2)地球离太阳约有1亿五千万千米;
(3)地球上煤的储量估计15万亿吨以上;
(4)纳米是长度单位,1纳米=0.000 001毫米.
(5)石墨烯目前是世界上最薄却最坚硬的纳米材料,它的理论厚度
0.000 000 000 34米.
在生活中,我们还会遇到一些较大或较小的数.例如:
这些较大或较小的数,读和写起来很麻烦,有没有简单的表示方法呢?
知识点1 用科学记数法表示较大的数
问题1
根据乘方计算:
101=___, 102=____,103=_________,104=_______,
106=_________,1010=_____________,….
10
100
1000
10000
1000000
10000000000
指数与运算结果中的0的个数有什么关系?
指数与运算结果的数位有什么关系?
知识点
用科学记数法表示较大的数
1
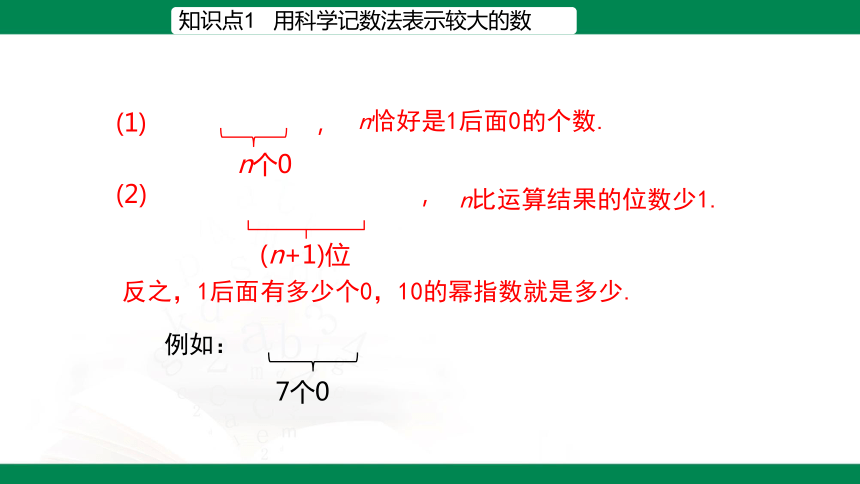
知识点1 用科学记数法表示较大的数
反之,1后面有多少个0,10的幂指数就是多少.
(1) ,
n个0
(2) ,
(n+1)位
7个0
例如:
n恰好是1后面0的个数.
n比运算结果的位数少1.
知识点1 用科学记数法表示较大的数
试一试:1. 把下列各数写成10的幂(即写成10())的形式:
100 ,10000,100000000,
2.300=3×100=3×10( )
32000=3.2×10000=3.2×10( )345000000=3.45×100000000=3.45×10( )
100=102 10000=104 100000000=108
2
4
8
读作“3.45乘10的8次方(幂)”
观察:等号左边的位数与右边10的指数有什么关系?
右边10的指数等于左边整数位数减1
知识点1 用科学记数法表示较大的数
定义:把一个较大或较小的数写成 (1≤a<10,n为整数)的形式,这种记数方法叫作科学记数法.
为了记数的方便和表示形式的规范,我们作如下规定:
归纳: 用科学记数法表示一个较大的数时,即写成 (1≤a<10,n为整数)的形式.
此时,n为正整数,n等于原数整数位减去1.
知识点1 用科学记数法表示较大的数
例 1 用科学记数法表示下列各数:
1 000 000,57 000 000,123 000 000 000
解:1 000 000=106;
57 000 000=5.7×107;
123 000 000 000=1.23×1011.
是5和8
用科学记数法表示一个n位整数,其中10的指数是_____.
n-1
思考:如果一个数是6位整数,用科学记数法表示它时,10的指数
是多少?如果一个数是9位整数呢?
知识点1 用科学记数法表示较大的数
探究
计算:
那么, 0.000 007 7=7.7 ×0.000001=7.7 ×10-6.
0.000 001=1 ×0.000001=1 ×10-6.
知识点2 用科学记数法表示小于1的正数
归纳: 用科学记数法也可以把一个较小的数写成
(1≤a<10,n为整数)的形式.
此时,n为负整数,n的绝对值等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面这个零).
知识点2 用科学记数法表示小于1的正数
例2 用科学记数法表示下列各数:
(1) 3 515 000;
(2) 10 300 000;
(3) 0.000 005;
(4) 0.000 000 012.
解:(1) 3 515 000=3.515×1 000 000=3.515×106;
(2) 10 300 000=1.03×10 000 000=1.03×107;
(3) 0.000 005=5×0.000 001=5×10-6;
(4) 0.000 000 012=1.2×0.000 000 01=1.2×10-8.
知识点2 用科学记数法表示小于1的正数
例2 光年是一个长度单位,是指光行走一年的距离,一般被用于计算恒星间的距离.
(1) 已知光的速度约为3×105km/s,如果按1年为365天,每天8.64×104 s计算,1光年约等于多少千米?(结果用科学记
数法表示)
(2) 太阳系以外离地球最近的恒星是比邻星,它与地球的距离
大约为3.99×1013 km.比邻星与地球的距离约合多少光年?
知识点2 用科学记数法表示小于1的正数
解:(1) 3×105×8.64×104×365
=9460.8×109
≈9.4608×1012(千米);
(2) 3.99×1013÷(9.46×1012)
≈0.422×10
=4.22(光年)
答:1光年约等于9.46×1012千米,比邻星与地球的距离约合4.22光年.
知识点2 用科学记数法表示小于1的正数
1. 2024年6月6日,嫦娥六号在距离地球
约 外上演“太空牵手”,完成月球轨道的交会对接.
数据384 000用科学记数法表示为( )
B
A. B.
C. D.
返回
2. 刻蚀机是芯片制造和微观加工最核心的设备之一,中国自
主研发的5纳米刻蚀机已获成功,5纳米就是 米.
数据 用科学记数法表示为( )
B
A. B.
C. D.
返回
3. 水质指纹污染溯源技术是一项水环境监管
技术,被称为水环境治理的“福尔摩斯”,经测算,一个水分
子的直径约有,数据 用科学记数
法表示为,则 的值为____.
返回
4. 中国信息通信研究院测算, 年,
中国 商用带动的信息消费规模将超过8万亿元,直接带动
经济总产出达10.6万亿元.其中数据10.6万亿用科学记数法表
示为___________.
【点拨】10.6万亿 .
返回
5. 已知的氢气质量约为 .
(1)用科学记数法表示 的氢气质量.
【解】 .
(2) 的氢气质量为多少克(结果用科学记数法表示)?
.
答:的氢气质量为 .
返回
6. [2024唐山模拟] “中国天眼”是目前世界上最大单口径、最
灵敏的射电望远镜.从理论上说,“中国天眼”能接收到137亿
光年以外的电磁信号,这个距离接近宇宙边缘.已知1光年
,结合估算,把137亿光年用科学记数法表
示为,则 的值为( )
C
A. 15 B. 16 C. 23 D. 24
【点拨】137亿光年 亿
, .故选C.
返回
7. 河北省物产丰富,土地辽阔,土地面积约
为19万平方千米.将19万用科学记数法表示为 ,关
于 的描述,下列说法正确的是____(填序号).
为负数;② ;
③ 等于19万的整数位数;
④当 增加1时,原数扩大为原来的10倍.
④
【点拨】万用科学记数法表示为 ,
选项错误,不符合题意; 当 增加1时,
原数扩大为原来的10倍,④正确,符合题意.
返回
8. 根据有关理论,当一颗恒星衰老时,其中
心的燃料(氢)已经被耗尽,在外壳的重压之下,核心开始
坍缩,直到最后形成体积小、密度大的星体.如果这一星体的
质量超过太阳质量的三倍,那么就会引发另一次大坍缩.当这
种收缩使得它的半径达到施瓦氏半径后,其引力就会变得相
当强大,以至于光也不能逃脱出来,从而成为一个看不见的
星体——黑洞.施瓦氏半径(单位: )的计算公式是
,其中 ,为万有引力常
数,表示星球的质量(单位:), ,为
光在真空中的速度.已知太阳质量为 ,计算太阳的
施瓦氏半径(结果保留三位有效数字).
科学记数法
定义
应用
把一个较大或较小的数写成a×10n(1≤a<10,n为整数)的形式,这种记数方法叫作科学记数法.
用科学记数法表示较大的数:n等于原数整数位减去1.
用科学记数法表示较小的数:n的绝对值等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面的零).
谢谢观看!
冀教版2024教材数学七年级下册
8.6 科学记数法
授课教师:********
班 级:********
时 间:********
第八章 整式的乘法
学习目标
1.会用科学记数法表示小于1的正数.
2.能将科学记数法表示的数还原成原数.
我将为你设计一份详细的二元一次方程组教案,重点突出概念讲解、解法推导及实际应用,帮助学生深入理解和掌握相关知识。
# 二元一次方程组教案
## 一、教学目标
1. 知识与技能目标
- 理解二元一次方程、二元一次方程组及其解的概念。
- 熟练掌握用代入消元法和加减消元法解二元一次方程组。
- 能根据实际问题列出二元一次方程组并求解,体会方程组是刻画现实世界中含有两个未知数的问题的有效数学模型。
2. 过程与方法目标
- 通过对实际问题的分析,经历从实际问题中抽象出数学模型的过程,提高分析问题和解决问题的能力。
- 在探索二元一次方程组解法的过程中,体会消元思想,培养学生的化归意识和运算能力。
3. 情感态度与价值观目标
- 感受数学与生活的紧密联系,激发学生学习数学的兴趣。
- 在合作交流中,培养学生的团队合作精神和创新意识。
## 二、教学重难点
1. **教学重点**
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组。
- 用二元一次方程组解决实际问题。
2. **教学难点**
- 理解消元思想,掌握消元的方法将二元一次方程组转化为一元一次方程。
- 从实际问题中找出等量关系,列出二元一次方程组。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
### (一)导入新课(5分钟)
1. 展示问题情境:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
2. 引导学生思考:
- 你能根据问题中的等量关系列出方程吗?
- 如果设两个未知数,如何表示这些等量关系?
### (二)讲授新课(30分钟)
1. **二元一次方程的概念**
- 引导学生设胜x场,负y场,根据等量关系列出方程:x + y = 10,2x + y = 16。
- 观察这两个方程的特点,总结二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。
- 举例让学生判断哪些是二元一次方程,如3x - 2y = 5,xy = 1等,加深对概念的理解。
2. **二元一次方程组的概念**
- 像这样把两个二元一次方程合在一起,就组成了一个二元一次方程组。
- 强调二元一次方程组中两个方程共含有两个相同的未知数。
3. **二元一次方程组的解**
- 让学生尝试找出满足方程组x + y = 10,2x + y = 16的x和y的值。
- 给出二元一次方程组的解的定义:一般地,使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
- 通过具体例子,让学生理解方程组的解是一对数,并且要同时满足方程组中的两个方程。
4. **代入消元法解二元一次方程组**
- 以方程组x + y = 10,2x + y = 16为例,讲解代入消元法。
- 分析:由方程x + y = 10可得y = 10 - x,将其代入方程2x + y = 16中,就可以消去y,得到一个关于x的一元一次方程。
- 详细讲解解题步骤:
- 由方程①得:y = 10 - x ③
- 把③代入②得:2x + (10 - x) = 16
- 解这个方程:2x + 10 - x = 16,x = 6
- 把x = 6代入③得:y = 10 - 6 = 4
- 所以方程组的解为x = 6,y = 4
- 总结代入消元法的步骤:
- 变形:从方程组中选一个系数比较简单的方程,将这个方程中的一个未知数用含另一个未知数的代数式表示出来。
- 代入:将变形后的式子代入另一个方程,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入变形后的式子,求出另一个未知数的值。
- 写解:写出方程组的解。
5. **加减消元法解二元一次方程组**
- 给出方程组2x + 3y = 11,2x - 5y = -1,引导学生观察两个方程中x的系数相同。
- 讲解:可以将两个方程相减,消去x,得到关于y的一元一次方程。
- 具体步骤:
- 用方程① - ②得:(2x + 3y) - (2x - 5y) = 11 - (-1)
- 去括号得:2x + 3y - 2x + 5y = 11 + 1
- 合并同类项得:8y = 12
- 解得:y = 1.5
- 把y = 1.5代入①得:2x + 3×1.5 = 11
- 解这个方程得:2x = 11 - 4.5,2x = 6.5,x = 3.25
- 所以方程组的解为x = 3.25,y = 1.5
- 总结加减消元法的步骤:
- 观察:观察方程组中两个方程相同未知数的系数特点。
- 变形:如果相同未知数的系数相等或互为相反数,则直接进行加减消元;如果系数不相等也不互为相反数,通过乘以适当的数,使某个未知数的系数相等或互为相反数。
- 加减:将两个方程相加或相减,消去一个未知数,得到一个一元一次方程。
- 求解:解这个一元一次方程,求出一个未知数的值。
- 回代:将求得的未知数的值代入原方程组中的一个方程,求出另一个未知数的值。
- 写解:写出方程组的解。
### (三)课堂练习(15分钟)
1. 给出一些二元一次方程、二元一次方程组,让学生判断并说明理由。
2. 用代入消元法和加减消元法解简单的二元一次方程组,如x - y = 3,3x - 8y = 14等,找学生板演,教师巡视指导,及时纠正学生的错误。
3. 出示一道实际问题:某班去看演出,甲种票每张24元,乙种票每张18元。如果35名学生购票恰好用去750元,甲乙两种票各买了多少张?引导学生分析问题,找出等量关系,列出二元一次方程组并求解。
### (四)课堂小结(5分钟)
1. 与学生一起回顾本节课所学内容:
- 二元一次方程、二元一次方程组及其解的概念。
- 代入消元法和加减消元法解二元一次方程组的步骤和方法。
- 用二元一次方程组解决实际问题的一般步骤。
2. 强调重点和难点,鼓励学生在课后多做练习,巩固所学知识。
### (五)布置作业(5分钟)
1. 基础作业:课本课后练习题,用代入消元法和加减消元法解给定的二元一次方程组。
2. 拓展作业:寻找生活中的实际问题,用二元一次方程组来解决,并写成小报告形式。
## 五、教学反思
在本节课的教学过程中,要注重引导学生从实际问题出发,逐步理解二元一次方程组的相关概念和解法。在讲解代入消元法和加减消元法时,要让学生充分理解消元的思想,通过大量的练习让学生熟练掌握两种解法。同时,在解决实际问题时,要培养学生分析问题、找出等量关系的能力。在教学过程中,要关注学生的反应,及时调整教学节奏和方法,确保学生能够理解和掌握所学内容。
这份教案从导入到作业布置,涵盖教学各环节。你看看是否符合你的教学需求,若有调整方向,如增减某部分内容,可随时告诉我。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
1000=
1000 000=
1000 000 000=
1000 000 000 000=
103
106
109
1012
100 …… 00
n个0
=10n
思考:如果1个1后边有n个0,这样的数可以简记作什么?
记作:10n
观察
光速300 000 000米/秒
太阳半径约696 000千米
PM2.5是指大气中直径小于或等于0.000 0025 m的颗粒物
人体红细胞的平均直径为0.000 007 7m
(1)第六次人口普查时,中国人口约为1370000000人;
(2)地球离太阳约有1亿五千万千米;
(3)地球上煤的储量估计15万亿吨以上;
(4)纳米是长度单位,1纳米=0.000 001毫米.
(5)石墨烯目前是世界上最薄却最坚硬的纳米材料,它的理论厚度
0.000 000 000 34米.
在生活中,我们还会遇到一些较大或较小的数.例如:
这些较大或较小的数,读和写起来很麻烦,有没有简单的表示方法呢?
知识点1 用科学记数法表示较大的数
问题1
根据乘方计算:
101=___, 102=____,103=_________,104=_______,
106=_________,1010=_____________,….
10
100
1000
10000
1000000
10000000000
指数与运算结果中的0的个数有什么关系?
指数与运算结果的数位有什么关系?
知识点
用科学记数法表示较大的数
1
知识点1 用科学记数法表示较大的数
反之,1后面有多少个0,10的幂指数就是多少.
(1) ,
n个0
(2) ,
(n+1)位
7个0
例如:
n恰好是1后面0的个数.
n比运算结果的位数少1.
知识点1 用科学记数法表示较大的数
试一试:1. 把下列各数写成10的幂(即写成10())的形式:
100 ,10000,100000000,
2.300=3×100=3×10( )
32000=3.2×10000=3.2×10( )345000000=3.45×100000000=3.45×10( )
100=102 10000=104 100000000=108
2
4
8
读作“3.45乘10的8次方(幂)”
观察:等号左边的位数与右边10的指数有什么关系?
右边10的指数等于左边整数位数减1
知识点1 用科学记数法表示较大的数
定义:把一个较大或较小的数写成 (1≤a<10,n为整数)的形式,这种记数方法叫作科学记数法.
为了记数的方便和表示形式的规范,我们作如下规定:
归纳: 用科学记数法表示一个较大的数时,即写成 (1≤a<10,n为整数)的形式.
此时,n为正整数,n等于原数整数位减去1.
知识点1 用科学记数法表示较大的数
例 1 用科学记数法表示下列各数:
1 000 000,57 000 000,123 000 000 000
解:1 000 000=106;
57 000 000=5.7×107;
123 000 000 000=1.23×1011.
是5和8
用科学记数法表示一个n位整数,其中10的指数是_____.
n-1
思考:如果一个数是6位整数,用科学记数法表示它时,10的指数
是多少?如果一个数是9位整数呢?
知识点1 用科学记数法表示较大的数
探究
计算:
那么, 0.000 007 7=7.7 ×0.000001=7.7 ×10-6.
0.000 001=1 ×0.000001=1 ×10-6.
知识点2 用科学记数法表示小于1的正数
归纳: 用科学记数法也可以把一个较小的数写成
(1≤a<10,n为整数)的形式.
此时,n为负整数,n的绝对值等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面这个零).
知识点2 用科学记数法表示小于1的正数
例2 用科学记数法表示下列各数:
(1) 3 515 000;
(2) 10 300 000;
(3) 0.000 005;
(4) 0.000 000 012.
解:(1) 3 515 000=3.515×1 000 000=3.515×106;
(2) 10 300 000=1.03×10 000 000=1.03×107;
(3) 0.000 005=5×0.000 001=5×10-6;
(4) 0.000 000 012=1.2×0.000 000 01=1.2×10-8.
知识点2 用科学记数法表示小于1的正数
例2 光年是一个长度单位,是指光行走一年的距离,一般被用于计算恒星间的距离.
(1) 已知光的速度约为3×105km/s,如果按1年为365天,每天8.64×104 s计算,1光年约等于多少千米?(结果用科学记
数法表示)
(2) 太阳系以外离地球最近的恒星是比邻星,它与地球的距离
大约为3.99×1013 km.比邻星与地球的距离约合多少光年?
知识点2 用科学记数法表示小于1的正数
解:(1) 3×105×8.64×104×365
=9460.8×109
≈9.4608×1012(千米);
(2) 3.99×1013÷(9.46×1012)
≈0.422×10
=4.22(光年)
答:1光年约等于9.46×1012千米,比邻星与地球的距离约合4.22光年.
知识点2 用科学记数法表示小于1的正数
1. 2024年6月6日,嫦娥六号在距离地球
约 外上演“太空牵手”,完成月球轨道的交会对接.
数据384 000用科学记数法表示为( )
B
A. B.
C. D.
返回
2. 刻蚀机是芯片制造和微观加工最核心的设备之一,中国自
主研发的5纳米刻蚀机已获成功,5纳米就是 米.
数据 用科学记数法表示为( )
B
A. B.
C. D.
返回
3. 水质指纹污染溯源技术是一项水环境监管
技术,被称为水环境治理的“福尔摩斯”,经测算,一个水分
子的直径约有,数据 用科学记数
法表示为,则 的值为____.
返回
4. 中国信息通信研究院测算, 年,
中国 商用带动的信息消费规模将超过8万亿元,直接带动
经济总产出达10.6万亿元.其中数据10.6万亿用科学记数法表
示为___________.
【点拨】10.6万亿 .
返回
5. 已知的氢气质量约为 .
(1)用科学记数法表示 的氢气质量.
【解】 .
(2) 的氢气质量为多少克(结果用科学记数法表示)?
.
答:的氢气质量为 .
返回
6. [2024唐山模拟] “中国天眼”是目前世界上最大单口径、最
灵敏的射电望远镜.从理论上说,“中国天眼”能接收到137亿
光年以外的电磁信号,这个距离接近宇宙边缘.已知1光年
,结合估算,把137亿光年用科学记数法表
示为,则 的值为( )
C
A. 15 B. 16 C. 23 D. 24
【点拨】137亿光年 亿
, .故选C.
返回
7. 河北省物产丰富,土地辽阔,土地面积约
为19万平方千米.将19万用科学记数法表示为 ,关
于 的描述,下列说法正确的是____(填序号).
为负数;② ;
③ 等于19万的整数位数;
④当 增加1时,原数扩大为原来的10倍.
④
【点拨】万用科学记数法表示为 ,
选项错误,不符合题意; 当 增加1时,
原数扩大为原来的10倍,④正确,符合题意.
返回
8. 根据有关理论,当一颗恒星衰老时,其中
心的燃料(氢)已经被耗尽,在外壳的重压之下,核心开始
坍缩,直到最后形成体积小、密度大的星体.如果这一星体的
质量超过太阳质量的三倍,那么就会引发另一次大坍缩.当这
种收缩使得它的半径达到施瓦氏半径后,其引力就会变得相
当强大,以至于光也不能逃脱出来,从而成为一个看不见的
星体——黑洞.施瓦氏半径(单位: )的计算公式是
,其中 ,为万有引力常
数,表示星球的质量(单位:), ,为
光在真空中的速度.已知太阳质量为 ,计算太阳的
施瓦氏半径(结果保留三位有效数字).
科学记数法
定义
应用
把一个较大或较小的数写成a×10n(1≤a<10,n为整数)的形式,这种记数方法叫作科学记数法.
用科学记数法表示较大的数:n等于原数整数位减去1.
用科学记数法表示较小的数:n的绝对值等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面的零).
谢谢观看!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
