9.2 提公因式法 课件(共30张PPT)
文档属性
| 名称 | 9.2 提公因式法 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
冀教版2024教材数学七年级下册
9.2 提公因式法
授课教师:********
班 级:********
时 间:********
第九章 因式分解
学习目标
1.了解公因式及提公因式的方法,并能正确确定公因式.
2.能熟练运用提公因式法进行因式分解,提升运算能力.
3.进一步理解因式分解的意义,强化代数推理的意识,感受整体思想的应用.
一、教学目标
理解因式分解的概念,掌握因式分解与整式乘法的关系。
熟练运用提公因式法、公式法(平方差公式、完全平方公式)进行因式分解。
通过因式分解的学习,培养学生观察、分析、归纳的能力,以及逆向思维能力。
二、教学重难点
(一)教学重点
因式分解的概念。
用提公因式法和公式法进行因式分解。
(二)教学难点
正确识别多项式各项的公因式。
灵活运用公式法进行因式分解,尤其是对公式的结构特征的理解和运用。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入(5 分钟)
计算:(x + 2)(x - 2) 与 x - 4;(a + b) 与 a + 2ab + b 。
提问:观察上述两组式子,从左到右和从右到左的变形有什么不同?引入本节课主题 —— 因式分解。
(二)新授(25 分钟)
因式分解的概念
给出定义:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式。
举例说明:如 x - 4 = (x + 2)(x - 2),a + 2ab + b = (a + b) 是因式分解,而 (x + 2)(x - 2) = x - 4,(a + b) = a + 2ab + b 是整式乘法,强调因式分解与整式乘法是互逆的恒等变形。
提公因式法
展示多项式:ma + mb + mc,分析各项都含有一个公共的因式 m,引出公因式的概念。
提公因式法定义:一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法。
例 1:分解因式 3x - 6xy + 3x。
分析:各项公因式为 3x。
解答过程:3x - 6xy + 3x = 3x (x - 2y + 1)。
公式法
平方差公式
回顾平方差公式:(a + b)(a - b) = a - b ,逆向得到因式分解的平方差公式:a - b = (a + b)(a - b)。
强调公式特点:等号左边是两项式,这两项都能写成平方的形式,且符号相反;等号右边是这两个数的和与这两个数的差的积。
例 2:分解因式 9x - 16y 。
分析:9x = (3x) ,16y = (4y) ,符合平方差公式。
解答:9x - 16y = (3x + 4y)(3x - 4y)。
完全平方公式
回顾完全平方公式:(a + b) = a + 2ab + b ,(a - b) = a - 2ab + b ,逆向得到因式分解的完全平方公式:a + 2ab + b = (a + b) ,a - 2ab + b = (a - b) 。
强调公式特点:等号左边是三项式,首末两项是两个数的平方,且符号相同,中间一项是这两个数乘积的 2 倍。
例 3:分解因式 4x + 12xy + 9y 。
分析:4x = (2x) ,9y = (3y) ,12xy = 2×2x×3y,符合完全平方公式。
解答:4x + 12xy + 9y = (2x + 3y) 。
(三)练习(15 分钟)
分解因式:
5x - 10x
16 - 25x
x + 10x + 25
让学生板演,教师巡视指导,及时纠正学生出现的错误。
(四)课堂小结(8 分钟)
与学生一起回顾因式分解的概念、提公因式法和公式法(平方差公式、完全平方公式)。
强调因式分解的注意事项:
分解要彻底,直到不能再分解为止。
公因式要提尽。
注意公式的结构特征,正确运用公式。
(五)作业布置(2 分钟)
课本课后习题。
拓展作业:尝试分解因式 x - 4x。
五、教学反思
在教学过程中,应注重引导学生理解因式分解的概念和方法,通过大量实例和练习让学生熟练掌握提公因式法和公式法。同时,要关注学生在找公因式、运用公式时容易出现的错误,及时给予指导和纠正。对于学有余力的学生,可提供一些拓展性的题目,进一步提高他们的思维能力。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
把一个多项式化成几个整式乘积的形式,叫作多项式的因式分解,也叫作将多项式分解因式.
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
分解因式:
等式的特征:左边是多项式,右边是几个整式的乘积.
复习: 什么叫作因式分解?
问题1:多项式ma+mb+mc有哪几项?
问题2:每一项的因式都分别有哪些?
问题3:这些项中有没有相同的因式,若有,相同的因式是什么?
ma, mb, mc
依次为m, a和m, b和m, c
有,为m
问题4:请说出多项式ab2-2a2b中各项的相同的因式.
ab
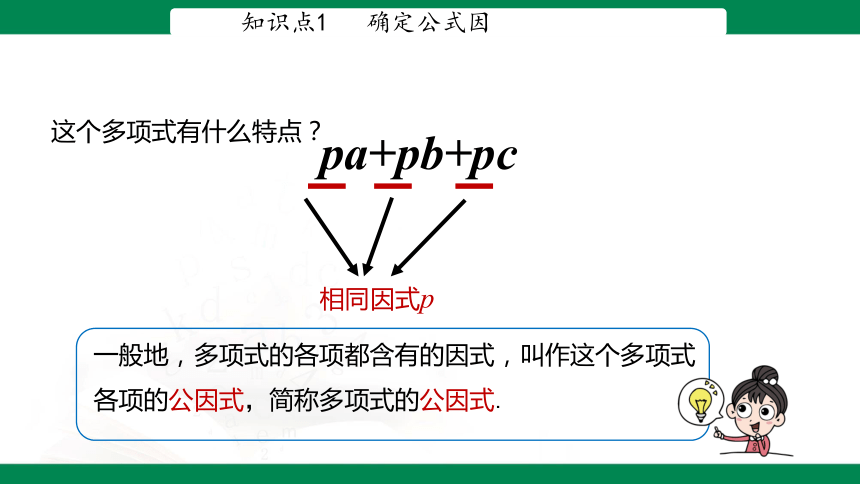
相同因式p
这个多项式有什么特点?
pa+pb+pc
一般地,多项式的各项都含有的因式,叫作这个多项式各项的公因式,简称多项式的公因式.
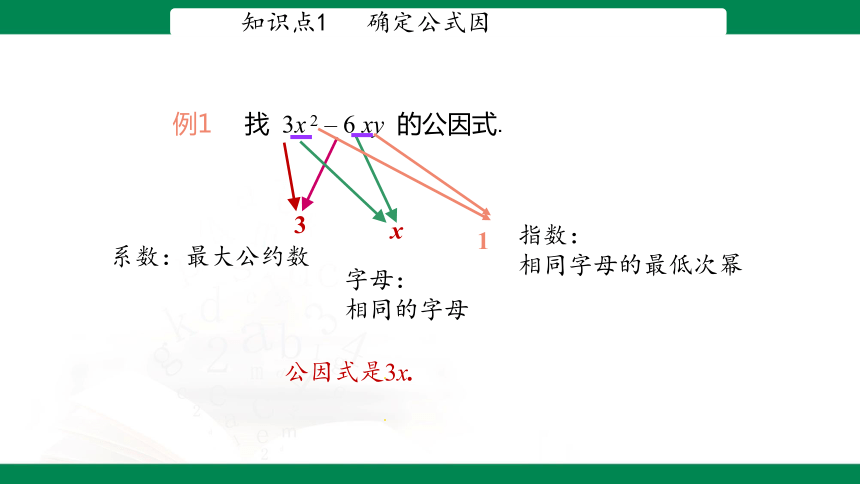
知识点1 确定公式因
例1 找 3x 2 – 6 xy 的公因式.
系数:最大公约数
3
字母:
相同的字母
x
公因式是3x.
指数:
相同字母的最低次幂
1
知识点1 确定公式因
正确找出多项式各项公因式的关键
1.定系数:公因式的系数是多项式各项系数的最大公约数.
2.定字母:字母取多项式各项中都含有的相同的字母. 3.定指数:相同字母的指数取各项中最小的一个,即字母最低次幂.
知识点1 确定公式因
例 2 写出下列多项式的公因式.
(1)6x-9x2;
(2)abc+2a;
(3)abc-ab2+2ab;
(4)2x2y+4xy2-6xy.
3x
a
ab
2xy
知识点1 确定公式因
问题:ma+mb+mc=m( )
ab2-2a2b=ab( )
(提示,逆用乘法分配律)
逆用乘法对加法的分配律,可以把公因式提到括号外边作为积的一个因式,从而将多项式化成两个因式乘积的形式.这种将多项式分解因式的方法,叫作提公因式法.
a+b+c
b-2a
知识点2 提公因式法分解因式
思考:以下是三名同学对多项式2x2+4x分解因式的结果:
(1)2x2+4x = 2(x2+2x);
(2)2x2+4x = x(2x+4);
(3) 2x2+4x = 2x(x+2).
第几位同学的结果是正确的?
用提公因式法分解因式应注意哪些问题呢?
知识点2 提公因式法分解因式
(3)是正确的.
(1) 8a3b2 + 12ab3c;
例3 把下列各式分解因式
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
(2) 2a(b+c) - 3(b+c).
公因式既可以是一个单项式的形式,也可以是一个多项式的形式.
知识点2 提公因式法分解因式
解:(1) 8a3b2 + 12ab3c
=4ab2 ·2a2+4ab2 ·3bc
=4ab2(2a2+3bc).
如果提出公因式4ab,另一个因式是否还有公因式?
另一个因式将是2a2b+3b2c,
它还有公因式b.
(2) 2a(b+c)-3(b+c)
=(b+c)(2a-3).
如何检查因式分解是否正确?
做整式乘法运算.
知识点2 提公因式法分解因式
整体思想是数学中一种重
要而且常用的思想方法.
把12x2y+18xy2分解因式.
解:原式 =3xy(4x + 6y).
错误
公因式没有提尽,还可以提出公因式2.
注意:公因式要提尽.
正解:原式=6xy(2x+3y).
小明的解法有误吗?
知识点2 提公因式法分解因式
当多项式的某一项和公因式相同时,提公因式后剩余的项是1.
错误
注意:某项提出勿漏1.
解:原式 =x(3x-6y).
把3x2 - 6xy+x分解因式.
正解:原式=3x·x-6y·x+1·x
=x(3x-6y+1).
小亮的解法有误吗?
知识点2 提公因式法分解因式
提出负号时括号里的项没变号.
错误
把 - x2+xy-xz分解因式.
解:原式= - x(x+y-z).
注意:首项有负常提负.
正解:原式= - (x2-xy+xz)
=- x(x-y+z).
小华的解法有误吗?
知识点2 提公因式法分解因式
例 4 把下列多项式分解因式:
(1)3a3b+9a2b2-3a2b; (2)-3x2+6xy-3xz.
解:(1)3a3b+9a2b2-3a2b
=3a2b·a+3a2b·3b-3a2b·1
=3a2b(a+3b-1).
知识点2 提公因式法分解因式
(2) -3x2+6xy-3xz
=(-3x)·x+(-3x)·(-2y)+(-3x)·z
=-3x·(x-2y+z).
例 5 分解因式:3x(a-b)+2(b-a).
解: 3x(a-b)+2(b-a)
=3x(a-b)-2(a-b)
=(a-b)(3x-2).
知识点2 提公因式法分解因式
例 6 计算:
(1)39×37-13×91;
(2)29×20.25+72×20.25+13×20.25-20.25×14.
(2)原式=20.25×(29+72+13-14)=2 025.
=13×20=260.
解:(1)原式=3×13×37-13×91
=13×(3×37-91)
方法总结:在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.
知识点2 提公因式法分解因式
例 7 已知a+b=7,ab=4,求a2b+ab2的值.
∴原式=ab(a+b)=4×7=28.
解:∵a+b=7,ab=4,
方法总结:含a±b,ab的求值题,通常要将所求代数式进行因式分解,将其变形为能用a±b和ab表示的式子,然后将a±b,ab的值整体带入即可.
知识点2 提公因式法分解因式
1. [2024菏泽期末] 多项式(, 均为
大于1的整数)各项的公因式是( )
B
A. B.
C. D.
2. [2024邢台模拟] 把 分解因式时,提出公
因式后,另一个因式是( )
A
A. B.
C. D.
返回
3. 把 因式分解,正
确的结果是( )
B
A. B.
C. D.
返回
4. 计算 的结果是( )
A
A. B.
C. D.
【点拨】 .
返回
5. 整式, ,下列结论:
结论一: .
结论二:,的公因式为 .
下列判断正确的是( )
A
A. 结论一正确,结论二不正确
B. 结论一不正确,结论二正确
C. 结论一、结论二都正确
D. 结论一、结论二都不正确
【点拨】,则,, 的公因
式是, 结论一正确,结论二不正确.故选A.
返回
6. 在处填入一个整式,使关于 的多项式
可以因式分解,则 可以为__________________
(写出一个即可).
(答案不唯一)
返回
7. 如图,长方形的长、
宽分别为,,且比 大3,面积为7,则
的值为____.
【点拨】由题意可知, ,
, .
21
返回
8. 教材P115习题T1 把下列各式分解因式:
(1) ;
【解】原式 .
(2) .
原式 .
返回
系数:各项系数的 .
提公因式法
确定
公因式
字母:各项 的字母
相同字母的指数取次数 .
最大公约数
相同
最低的
多项式的各项都含有的因式,叫作这个多项式各项的公因式,简称多项式的公因式.
逆用乘法对加法的分配律,可以把公因式提到括号外边作为积的一个因式,从而将多项式化成两个因式乘积的形式.这种将多项式分解因式的方法,叫作提公因式法.
谢谢观看!
冀教版2024教材数学七年级下册
9.2 提公因式法
授课教师:********
班 级:********
时 间:********
第九章 因式分解
学习目标
1.了解公因式及提公因式的方法,并能正确确定公因式.
2.能熟练运用提公因式法进行因式分解,提升运算能力.
3.进一步理解因式分解的意义,强化代数推理的意识,感受整体思想的应用.
一、教学目标
理解因式分解的概念,掌握因式分解与整式乘法的关系。
熟练运用提公因式法、公式法(平方差公式、完全平方公式)进行因式分解。
通过因式分解的学习,培养学生观察、分析、归纳的能力,以及逆向思维能力。
二、教学重难点
(一)教学重点
因式分解的概念。
用提公因式法和公式法进行因式分解。
(二)教学难点
正确识别多项式各项的公因式。
灵活运用公式法进行因式分解,尤其是对公式的结构特征的理解和运用。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入(5 分钟)
计算:(x + 2)(x - 2) 与 x - 4;(a + b) 与 a + 2ab + b 。
提问:观察上述两组式子,从左到右和从右到左的变形有什么不同?引入本节课主题 —— 因式分解。
(二)新授(25 分钟)
因式分解的概念
给出定义:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式。
举例说明:如 x - 4 = (x + 2)(x - 2),a + 2ab + b = (a + b) 是因式分解,而 (x + 2)(x - 2) = x - 4,(a + b) = a + 2ab + b 是整式乘法,强调因式分解与整式乘法是互逆的恒等变形。
提公因式法
展示多项式:ma + mb + mc,分析各项都含有一个公共的因式 m,引出公因式的概念。
提公因式法定义:一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法。
例 1:分解因式 3x - 6xy + 3x。
分析:各项公因式为 3x。
解答过程:3x - 6xy + 3x = 3x (x - 2y + 1)。
公式法
平方差公式
回顾平方差公式:(a + b)(a - b) = a - b ,逆向得到因式分解的平方差公式:a - b = (a + b)(a - b)。
强调公式特点:等号左边是两项式,这两项都能写成平方的形式,且符号相反;等号右边是这两个数的和与这两个数的差的积。
例 2:分解因式 9x - 16y 。
分析:9x = (3x) ,16y = (4y) ,符合平方差公式。
解答:9x - 16y = (3x + 4y)(3x - 4y)。
完全平方公式
回顾完全平方公式:(a + b) = a + 2ab + b ,(a - b) = a - 2ab + b ,逆向得到因式分解的完全平方公式:a + 2ab + b = (a + b) ,a - 2ab + b = (a - b) 。
强调公式特点:等号左边是三项式,首末两项是两个数的平方,且符号相同,中间一项是这两个数乘积的 2 倍。
例 3:分解因式 4x + 12xy + 9y 。
分析:4x = (2x) ,9y = (3y) ,12xy = 2×2x×3y,符合完全平方公式。
解答:4x + 12xy + 9y = (2x + 3y) 。
(三)练习(15 分钟)
分解因式:
5x - 10x
16 - 25x
x + 10x + 25
让学生板演,教师巡视指导,及时纠正学生出现的错误。
(四)课堂小结(8 分钟)
与学生一起回顾因式分解的概念、提公因式法和公式法(平方差公式、完全平方公式)。
强调因式分解的注意事项:
分解要彻底,直到不能再分解为止。
公因式要提尽。
注意公式的结构特征,正确运用公式。
(五)作业布置(2 分钟)
课本课后习题。
拓展作业:尝试分解因式 x - 4x。
五、教学反思
在教学过程中,应注重引导学生理解因式分解的概念和方法,通过大量实例和练习让学生熟练掌握提公因式法和公式法。同时,要关注学生在找公因式、运用公式时容易出现的错误,及时给予指导和纠正。对于学有余力的学生,可提供一些拓展性的题目,进一步提高他们的思维能力。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
把一个多项式化成几个整式乘积的形式,叫作多项式的因式分解,也叫作将多项式分解因式.
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
分解因式:
等式的特征:左边是多项式,右边是几个整式的乘积.
复习: 什么叫作因式分解?
问题1:多项式ma+mb+mc有哪几项?
问题2:每一项的因式都分别有哪些?
问题3:这些项中有没有相同的因式,若有,相同的因式是什么?
ma, mb, mc
依次为m, a和m, b和m, c
有,为m
问题4:请说出多项式ab2-2a2b中各项的相同的因式.
ab
相同因式p
这个多项式有什么特点?
pa+pb+pc
一般地,多项式的各项都含有的因式,叫作这个多项式各项的公因式,简称多项式的公因式.
知识点1 确定公式因
例1 找 3x 2 – 6 xy 的公因式.
系数:最大公约数
3
字母:
相同的字母
x
公因式是3x.
指数:
相同字母的最低次幂
1
知识点1 确定公式因
正确找出多项式各项公因式的关键
1.定系数:公因式的系数是多项式各项系数的最大公约数.
2.定字母:字母取多项式各项中都含有的相同的字母. 3.定指数:相同字母的指数取各项中最小的一个,即字母最低次幂.
知识点1 确定公式因
例 2 写出下列多项式的公因式.
(1)6x-9x2;
(2)abc+2a;
(3)abc-ab2+2ab;
(4)2x2y+4xy2-6xy.
3x
a
ab
2xy
知识点1 确定公式因
问题:ma+mb+mc=m( )
ab2-2a2b=ab( )
(提示,逆用乘法分配律)
逆用乘法对加法的分配律,可以把公因式提到括号外边作为积的一个因式,从而将多项式化成两个因式乘积的形式.这种将多项式分解因式的方法,叫作提公因式法.
a+b+c
b-2a
知识点2 提公因式法分解因式
思考:以下是三名同学对多项式2x2+4x分解因式的结果:
(1)2x2+4x = 2(x2+2x);
(2)2x2+4x = x(2x+4);
(3) 2x2+4x = 2x(x+2).
第几位同学的结果是正确的?
用提公因式法分解因式应注意哪些问题呢?
知识点2 提公因式法分解因式
(3)是正确的.
(1) 8a3b2 + 12ab3c;
例3 把下列各式分解因式
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
(2) 2a(b+c) - 3(b+c).
公因式既可以是一个单项式的形式,也可以是一个多项式的形式.
知识点2 提公因式法分解因式
解:(1) 8a3b2 + 12ab3c
=4ab2 ·2a2+4ab2 ·3bc
=4ab2(2a2+3bc).
如果提出公因式4ab,另一个因式是否还有公因式?
另一个因式将是2a2b+3b2c,
它还有公因式b.
(2) 2a(b+c)-3(b+c)
=(b+c)(2a-3).
如何检查因式分解是否正确?
做整式乘法运算.
知识点2 提公因式法分解因式
整体思想是数学中一种重
要而且常用的思想方法.
把12x2y+18xy2分解因式.
解:原式 =3xy(4x + 6y).
错误
公因式没有提尽,还可以提出公因式2.
注意:公因式要提尽.
正解:原式=6xy(2x+3y).
小明的解法有误吗?
知识点2 提公因式法分解因式
当多项式的某一项和公因式相同时,提公因式后剩余的项是1.
错误
注意:某项提出勿漏1.
解:原式 =x(3x-6y).
把3x2 - 6xy+x分解因式.
正解:原式=3x·x-6y·x+1·x
=x(3x-6y+1).
小亮的解法有误吗?
知识点2 提公因式法分解因式
提出负号时括号里的项没变号.
错误
把 - x2+xy-xz分解因式.
解:原式= - x(x+y-z).
注意:首项有负常提负.
正解:原式= - (x2-xy+xz)
=- x(x-y+z).
小华的解法有误吗?
知识点2 提公因式法分解因式
例 4 把下列多项式分解因式:
(1)3a3b+9a2b2-3a2b; (2)-3x2+6xy-3xz.
解:(1)3a3b+9a2b2-3a2b
=3a2b·a+3a2b·3b-3a2b·1
=3a2b(a+3b-1).
知识点2 提公因式法分解因式
(2) -3x2+6xy-3xz
=(-3x)·x+(-3x)·(-2y)+(-3x)·z
=-3x·(x-2y+z).
例 5 分解因式:3x(a-b)+2(b-a).
解: 3x(a-b)+2(b-a)
=3x(a-b)-2(a-b)
=(a-b)(3x-2).
知识点2 提公因式法分解因式
例 6 计算:
(1)39×37-13×91;
(2)29×20.25+72×20.25+13×20.25-20.25×14.
(2)原式=20.25×(29+72+13-14)=2 025.
=13×20=260.
解:(1)原式=3×13×37-13×91
=13×(3×37-91)
方法总结:在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.
知识点2 提公因式法分解因式
例 7 已知a+b=7,ab=4,求a2b+ab2的值.
∴原式=ab(a+b)=4×7=28.
解:∵a+b=7,ab=4,
方法总结:含a±b,ab的求值题,通常要将所求代数式进行因式分解,将其变形为能用a±b和ab表示的式子,然后将a±b,ab的值整体带入即可.
知识点2 提公因式法分解因式
1. [2024菏泽期末] 多项式(, 均为
大于1的整数)各项的公因式是( )
B
A. B.
C. D.
2. [2024邢台模拟] 把 分解因式时,提出公
因式后,另一个因式是( )
A
A. B.
C. D.
返回
3. 把 因式分解,正
确的结果是( )
B
A. B.
C. D.
返回
4. 计算 的结果是( )
A
A. B.
C. D.
【点拨】 .
返回
5. 整式, ,下列结论:
结论一: .
结论二:,的公因式为 .
下列判断正确的是( )
A
A. 结论一正确,结论二不正确
B. 结论一不正确,结论二正确
C. 结论一、结论二都正确
D. 结论一、结论二都不正确
【点拨】,则,, 的公因
式是, 结论一正确,结论二不正确.故选A.
返回
6. 在处填入一个整式,使关于 的多项式
可以因式分解,则 可以为__________________
(写出一个即可).
(答案不唯一)
返回
7. 如图,长方形的长、
宽分别为,,且比 大3,面积为7,则
的值为____.
【点拨】由题意可知, ,
, .
21
返回
8. 教材P115习题T1 把下列各式分解因式:
(1) ;
【解】原式 .
(2) .
原式 .
返回
系数:各项系数的 .
提公因式法
确定
公因式
字母:各项 的字母
相同字母的指数取次数 .
最大公约数
相同
最低的
多项式的各项都含有的因式,叫作这个多项式各项的公因式,简称多项式的公因式.
逆用乘法对加法的分配律,可以把公因式提到括号外边作为积的一个因式,从而将多项式化成两个因式乘积的形式.这种将多项式分解因式的方法,叫作提公因式法.
谢谢观看!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
