10.1 三角形的边 课件(共32张PPT)
文档属性
| 名称 | 10.1 三角形的边 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览






文档简介
(共32张PPT)
冀教版2024教材数学七年级下册
10.1 三角形的边
授课教师:********
班 级:********
时 间:********
第十章 三角形
学习目标
1.结合实例理解三角形及其顶点、边的概念,掌握三角形的表示方法.
2.掌握三角形的三边关系,会用三角形的三边关系判断任意三条线段能否组成三角形.
3.初步了解等腰三角形、 等边三角形的概念及其关系,会对三角形进行分类,感知分类讨论思想.
一、教学目标
理解因式分解的概念,掌握因式分解与整式乘法的关系。
熟练运用提公因式法、公式法(平方差公式、完全平方公式)进行因式分解。
通过因式分解的学习,培养学生观察、分析、归纳的能力,以及逆向思维能力。
二、教学重难点
(一)教学重点
因式分解的概念。
用提公因式法和公式法进行因式分解。
(二)教学难点
正确识别多项式各项的公因式。
灵活运用公式法进行因式分解,尤其是对公式的结构特征的理解和运用。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入(5 分钟)
计算:(x + 2)(x - 2) 与 x - 4;(a + b) 与 a + 2ab + b 。
提问:观察上述两组式子,从左到右和从右到左的变形有什么不同?引入本节课主题 —— 因式分解。
(二)新授(25 分钟)
因式分解的概念
给出定义:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式。
举例说明:如 x - 4 = (x + 2)(x - 2),a + 2ab + b = (a + b) 是因式分解,而 (x + 2)(x - 2) = x - 4,(a + b) = a + 2ab + b 是整式乘法,强调因式分解与整式乘法是互逆的恒等变形。
提公因式法
展示多项式:ma + mb + mc,分析各项都含有一个公共的因式 m,引出公因式的概念。
提公因式法定义:一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法。
例 1:分解因式 3x - 6xy + 3x。
分析:各项公因式为 3x。
解答过程:3x - 6xy + 3x = 3x (x - 2y + 1)。
公式法
平方差公式
回顾平方差公式:(a + b)(a - b) = a - b ,逆向得到因式分解的平方差公式:a - b = (a + b)(a - b)。
强调公式特点:等号左边是两项式,这两项都能写成平方的形式,且符号相反;等号右边是这两个数的和与这两个数的差的积。
例 2:分解因式 9x - 16y 。
分析:9x = (3x) ,16y = (4y) ,符合平方差公式。
解答:9x - 16y = (3x + 4y)(3x - 4y)。
完全平方公式
回顾完全平方公式:(a + b) = a + 2ab + b ,(a - b) = a - 2ab + b ,逆向得到因式分解的完全平方公式:a + 2ab + b = (a + b) ,a - 2ab + b = (a - b) 。
强调公式特点:等号左边是三项式,首末两项是两个数的平方,且符号相同,中间一项是这两个数乘积的 2 倍。
例 3:分解因式 4x + 12xy + 9y 。
分析:4x = (2x) ,9y = (3y) ,12xy = 2×2x×3y,符合完全平方公式。
解答:4x + 12xy + 9y = (2x + 3y) 。
(三)练习(15 分钟)
分解因式:
5x - 10x
16 - 25x
x + 10x + 25
让学生板演,教师巡视指导,及时纠正学生出现的错误。
(四)课堂小结(8 分钟)
与学生一起回顾因式分解的概念、提公因式法和公式法(平方差公式、完全平方公式)。
强调因式分解的注意事项:
分解要彻底,直到不能再分解为止。
公因式要提尽。
注意公式的结构特征,正确运用公式。
(五)作业布置(2 分钟)
课本课后习题。
拓展作业:尝试分解因式 x - 4x。
五、教学反思
在教学过程中,应注重引导学生理解因式分解的概念和方法,通过大量实例和练习让学生熟练掌握提公因式法和公式法。同时,要关注学生在找公因式、运用公式时容易出现的错误,及时给予指导和纠正。对于学有余力的学生,可提供一些拓展性的题目,进一步提高他们的思维能力。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
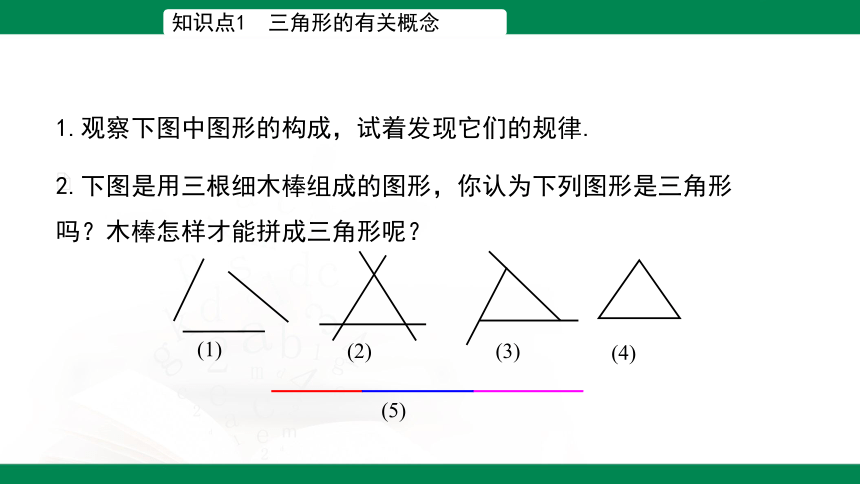
1.观察下图中图形的构成,试着发现它们的规律.
2.下图是用三根细木棒组成的图形,你认为下列图形是三角形吗?木棒怎样才能拼成三角形呢?
(4)
(1)
(3)
(2)
(5)
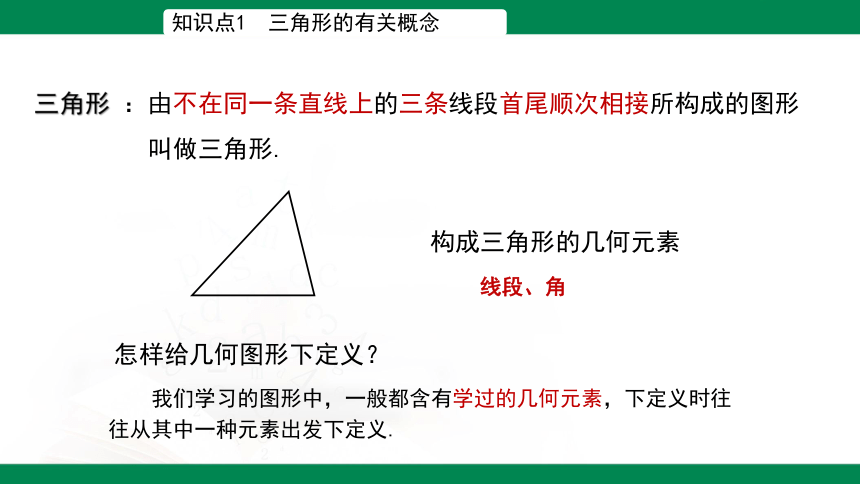
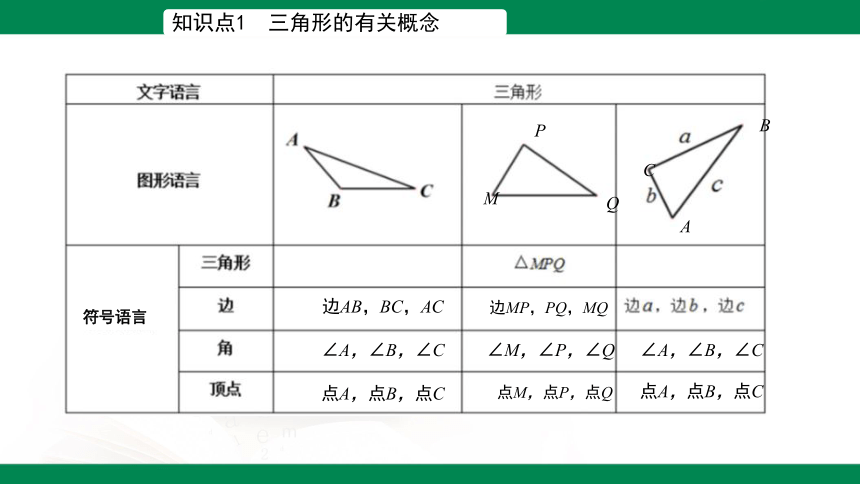
知识点1 三角形的有关概念
三角形 :由不在同一条直线上的三条线段首尾顺次相接所构成的图形
叫做三角形.
怎样给几何图形下定义?
我们学习的图形中,一般都含有学过的几何元素,下定义时往往从其中一种元素出发下定义.
构成三角形的几何元素
线段、角
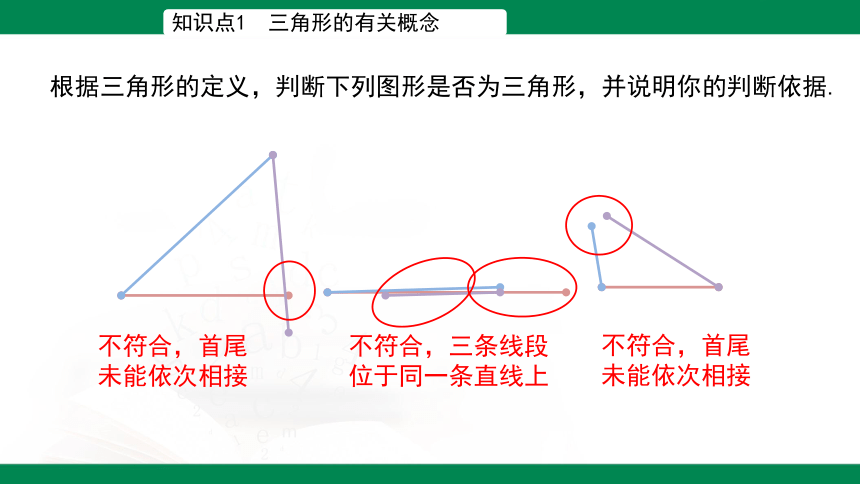
知识点1 三角形的有关概念
根据三角形的定义,判断下列图形是否为三角形,并说明你的判断依据.
不符合,首尾未能依次相接
不符合,三条线段位于同一条直线上
不符合,首尾未能依次相接
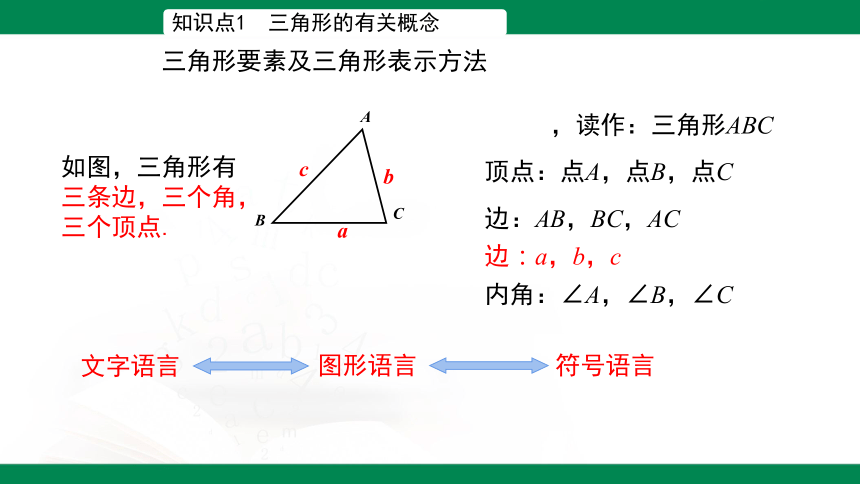
知识点1 三角形的有关概念
如图,三角形有
三条边,三个角,三个顶点.
A
B
C
顶点:点A,点B,点C
,读作:三角形ABC
边:AB,BC,AC
边:a,b,c
内角:∠A,∠B,∠C
a
b
c
文字语言
图形语言
符号语言
三角形要素及三角形表示方法
知识点1 三角形的有关概念
符号语言
B
C
A
点A,点B,点C
∠A,∠B,∠C
边AB,BC,AC
边MP,PQ,MQ
∠M,∠P,∠Q
点M,点P,点Q
∠A,∠B,∠C
点A,点B,点C
P
Q
M
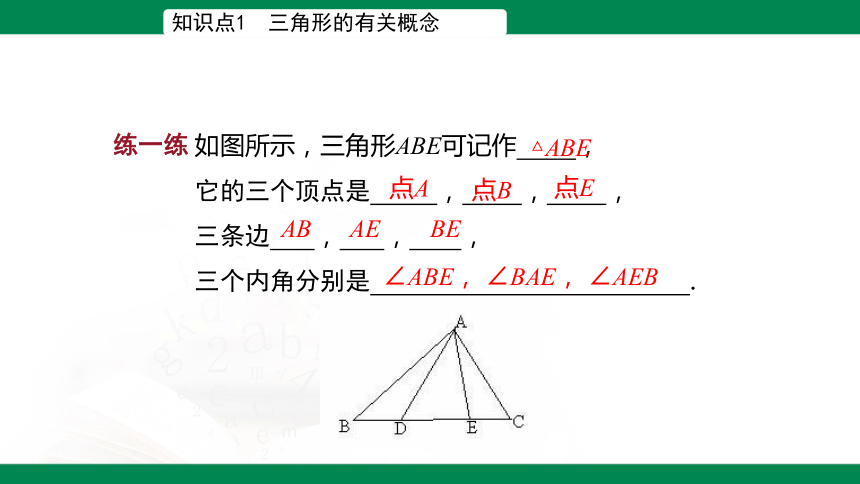
知识点1 三角形的有关概念
练一练
如图所示,三角形ABE可记作 ,
它的三个顶点是 , , ,
三条边 , , ,
三个内角分别是 .
△ABE
点A
点B
点E
AE
AB
BE
∠ABE, ∠BAE, ∠AEB
知识点1 三角形的有关概念
每组课前准备四根木条,分别长为2cm,3cm,4 cm,5cm,现在从其中任取三根相接来摆三角形,试试能否成功?做好实验记录,并分类汇总实验.
一起探究
知识点2 三角形的三边关系
实验数据记录在下表:
三根木棒的长度cm 能否构成三角形 任意两根木棒长度的和与第三根的关系 (用数字表示)
2,3,5
2,3,4
2,4,5
3,4,5
否
能
能
能
2+3=5,2+5>3 , 3+5>2
2+3>4,2+4>3 , 3+4>2
2+4>5,2+5>4 , 4+5>2
3+4>5,3+5>4 , 4+5>3
知识点2 三角形的三边关系
谈一谈:1.是不是任意三根木棒都能拼成三角形呢?谈谈哪些试验是失败的?找出失败的原因,并总结什么样的三条线段能拼成三角形?
2. 由以上探索,你能归纳出三角形任意两边之和与第三边的关系吗?
猜想:三角形任意两边之和大于第三边
如何说明呢?
知识点2 三角形的三边关系
B
A
C
已知△ABC.
说明:AB+AC>BC,
AC+BC>AB,AB+BC>AC
说理过程:∵AB是线段,
∴AC+BC>AB,(两点之间,线段最短)
同理可得:AB+BC>AC,AB+AC>BC.
归纳:三角形任意两边之和大于第三边.
知识点2 三角形的三边关系
例1 长度为6cm,4cm,3cm三条线段能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
这样判断需要三个条件,你一定希望有更好的判
断方法吧.想想看!
解: ∵最长线段是6cm
4+3>6
∴能组成三角形
判断三条线段能否组成三角形的方法:
①找出最长线段.
②比较较短两边之和与最长线段的大小
③判断能否组成三角形.
知识点2 三角形的三边关系
练一练 1.下列长度的三条线段能否组成三角形?
(1) 3,8,4
(2) 2,5,6
(3) 5,6,10
(4) 3,5,8
不能
能
能
不能
知识点2 三角形的三边关系
已知一个三角形的最小边为2cm,另两边分别为6cm和a cm , a的取值范围是什么?
知识点2 三角形的三边关系
大家谈谈:观察下图中的三角形,试着比较它们之间的不同之处.
提示:可根据三角形三边的长度关系进行比较
不等边三角形
(三条边长度均不相等)
等腰三角形
(两条边长度相等)
等边三角形
(三条边长相等)
顶角
底角
腰
底边
知识点3 三角形按边分类
归纳:三条边各不相等的三角形叫做不等边三角形;
有两条边相等的三角形叫做等腰三角形;
三条边都相等的三角形叫做等边三角形 .
等腰三角形与等边三角形的关系:
等边三角形是特殊的等边三角形,即底边和腰相等的 等腰三角形.
知识点3 三角形按边分类
三角形进行分类
两边相等的等腰三角形
三边相等的等腰三角形
等边三角形
三角形
等腰三角形
三边不等的三角形
按边分
不等边三角形
三角形
三边都不相等的三角形
等腰三角形
等边三角形
知识点3 三角形按边分类
1. [2024廊坊校级月考] 下面是四位同学分别用三根木棍组成
的图形,其中是三角形的是( )
A
A. B. C. D.
返回
2. 如图,以 为边的三角形有( )
D
(第2题)
A. 1个 B. 2个 C. 3个 D. 4个
返回
3. 教材P128练习T3 满足下列条件的三条线段,, ,
能构成三角形的是( )
C
A. B. ,
C. ,, D. ,
返回
(第4题)
4. [2024邢台校级期中] 如图表示的是三角形的
分类,则下列说法正确的是( )
C
A. 表示等边三角形
B. 表示锐角三角形
C. 表示等腰三角形
D. 表示三边都不相等的三角形
返回
5. 绝缘梯是电力工程的专用登高
工具,如图,在绝缘梯示意图中,, 的长
度都为,则, 两点之间的距离可能是
( )
A
A. B. C. D.
返回
6.如图,图中有___个三角形,含 的三角形为___________
______________,在中,的对角是_______, 的
对边是____.
6
,,
返回
7. 已知一个三角形的三条边的长分别为
,, .若这个三角形是等腰三角形,求它的三边
的长.
【解】
需分两种情况讨论:
①若,则 ,此时三边长分别为3,3,7,不
能构成三角形,舍去;
②若,则 ,此时三边长分别为5,9,9,能
构成三角形,符合题意.
综上,当这个三角形是等腰三角形时,三边长分别为5,9,9.
返回
8. [2024秦皇岛期末] 若使用如图所示的①、②两根直铁丝做
成一个三角形框架,则需要将其中一根铁丝分为两段,则下
列说法正确的是( )
C
A. ①②都可以分为两段 B. ①②都不可以分为两段
C. 只有①可以分为两段 D. 只有②可以分为两段
返回
三角形
概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
分类
不等边三角形
等腰三角形(包括等边三角形)
三边关系
任意两边之和大于第三边
谢谢观看!
冀教版2024教材数学七年级下册
10.1 三角形的边
授课教师:********
班 级:********
时 间:********
第十章 三角形
学习目标
1.结合实例理解三角形及其顶点、边的概念,掌握三角形的表示方法.
2.掌握三角形的三边关系,会用三角形的三边关系判断任意三条线段能否组成三角形.
3.初步了解等腰三角形、 等边三角形的概念及其关系,会对三角形进行分类,感知分类讨论思想.
一、教学目标
理解因式分解的概念,掌握因式分解与整式乘法的关系。
熟练运用提公因式法、公式法(平方差公式、完全平方公式)进行因式分解。
通过因式分解的学习,培养学生观察、分析、归纳的能力,以及逆向思维能力。
二、教学重难点
(一)教学重点
因式分解的概念。
用提公因式法和公式法进行因式分解。
(二)教学难点
正确识别多项式各项的公因式。
灵活运用公式法进行因式分解,尤其是对公式的结构特征的理解和运用。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入(5 分钟)
计算:(x + 2)(x - 2) 与 x - 4;(a + b) 与 a + 2ab + b 。
提问:观察上述两组式子,从左到右和从右到左的变形有什么不同?引入本节课主题 —— 因式分解。
(二)新授(25 分钟)
因式分解的概念
给出定义:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式。
举例说明:如 x - 4 = (x + 2)(x - 2),a + 2ab + b = (a + b) 是因式分解,而 (x + 2)(x - 2) = x - 4,(a + b) = a + 2ab + b 是整式乘法,强调因式分解与整式乘法是互逆的恒等变形。
提公因式法
展示多项式:ma + mb + mc,分析各项都含有一个公共的因式 m,引出公因式的概念。
提公因式法定义:一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法。
例 1:分解因式 3x - 6xy + 3x。
分析:各项公因式为 3x。
解答过程:3x - 6xy + 3x = 3x (x - 2y + 1)。
公式法
平方差公式
回顾平方差公式:(a + b)(a - b) = a - b ,逆向得到因式分解的平方差公式:a - b = (a + b)(a - b)。
强调公式特点:等号左边是两项式,这两项都能写成平方的形式,且符号相反;等号右边是这两个数的和与这两个数的差的积。
例 2:分解因式 9x - 16y 。
分析:9x = (3x) ,16y = (4y) ,符合平方差公式。
解答:9x - 16y = (3x + 4y)(3x - 4y)。
完全平方公式
回顾完全平方公式:(a + b) = a + 2ab + b ,(a - b) = a - 2ab + b ,逆向得到因式分解的完全平方公式:a + 2ab + b = (a + b) ,a - 2ab + b = (a - b) 。
强调公式特点:等号左边是三项式,首末两项是两个数的平方,且符号相同,中间一项是这两个数乘积的 2 倍。
例 3:分解因式 4x + 12xy + 9y 。
分析:4x = (2x) ,9y = (3y) ,12xy = 2×2x×3y,符合完全平方公式。
解答:4x + 12xy + 9y = (2x + 3y) 。
(三)练习(15 分钟)
分解因式:
5x - 10x
16 - 25x
x + 10x + 25
让学生板演,教师巡视指导,及时纠正学生出现的错误。
(四)课堂小结(8 分钟)
与学生一起回顾因式分解的概念、提公因式法和公式法(平方差公式、完全平方公式)。
强调因式分解的注意事项:
分解要彻底,直到不能再分解为止。
公因式要提尽。
注意公式的结构特征,正确运用公式。
(五)作业布置(2 分钟)
课本课后习题。
拓展作业:尝试分解因式 x - 4x。
五、教学反思
在教学过程中,应注重引导学生理解因式分解的概念和方法,通过大量实例和练习让学生熟练掌握提公因式法和公式法。同时,要关注学生在找公因式、运用公式时容易出现的错误,及时给予指导和纠正。对于学有余力的学生,可提供一些拓展性的题目,进一步提高他们的思维能力。
学习目录
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
1.观察下图中图形的构成,试着发现它们的规律.
2.下图是用三根细木棒组成的图形,你认为下列图形是三角形吗?木棒怎样才能拼成三角形呢?
(4)
(1)
(3)
(2)
(5)
知识点1 三角形的有关概念
三角形 :由不在同一条直线上的三条线段首尾顺次相接所构成的图形
叫做三角形.
怎样给几何图形下定义?
我们学习的图形中,一般都含有学过的几何元素,下定义时往往从其中一种元素出发下定义.
构成三角形的几何元素
线段、角
知识点1 三角形的有关概念
根据三角形的定义,判断下列图形是否为三角形,并说明你的判断依据.
不符合,首尾未能依次相接
不符合,三条线段位于同一条直线上
不符合,首尾未能依次相接
知识点1 三角形的有关概念
如图,三角形有
三条边,三个角,三个顶点.
A
B
C
顶点:点A,点B,点C
,读作:三角形ABC
边:AB,BC,AC
边:a,b,c
内角:∠A,∠B,∠C
a
b
c
文字语言
图形语言
符号语言
三角形要素及三角形表示方法
知识点1 三角形的有关概念
符号语言
B
C
A
点A,点B,点C
∠A,∠B,∠C
边AB,BC,AC
边MP,PQ,MQ
∠M,∠P,∠Q
点M,点P,点Q
∠A,∠B,∠C
点A,点B,点C
P
Q
M
知识点1 三角形的有关概念
练一练
如图所示,三角形ABE可记作 ,
它的三个顶点是 , , ,
三条边 , , ,
三个内角分别是 .
△ABE
点A
点B
点E
AE
AB
BE
∠ABE, ∠BAE, ∠AEB
知识点1 三角形的有关概念
每组课前准备四根木条,分别长为2cm,3cm,4 cm,5cm,现在从其中任取三根相接来摆三角形,试试能否成功?做好实验记录,并分类汇总实验.
一起探究
知识点2 三角形的三边关系
实验数据记录在下表:
三根木棒的长度cm 能否构成三角形 任意两根木棒长度的和与第三根的关系 (用数字表示)
2,3,5
2,3,4
2,4,5
3,4,5
否
能
能
能
2+3=5,2+5>3 , 3+5>2
2+3>4,2+4>3 , 3+4>2
2+4>5,2+5>4 , 4+5>2
3+4>5,3+5>4 , 4+5>3
知识点2 三角形的三边关系
谈一谈:1.是不是任意三根木棒都能拼成三角形呢?谈谈哪些试验是失败的?找出失败的原因,并总结什么样的三条线段能拼成三角形?
2. 由以上探索,你能归纳出三角形任意两边之和与第三边的关系吗?
猜想:三角形任意两边之和大于第三边
如何说明呢?
知识点2 三角形的三边关系
B
A
C
已知△ABC.
说明:AB+AC>BC,
AC+BC>AB,AB+BC>AC
说理过程:∵AB是线段,
∴AC+BC>AB,(两点之间,线段最短)
同理可得:AB+BC>AC,AB+AC>BC.
归纳:三角形任意两边之和大于第三边.
知识点2 三角形的三边关系
例1 长度为6cm,4cm,3cm三条线段能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
这样判断需要三个条件,你一定希望有更好的判
断方法吧.想想看!
解: ∵最长线段是6cm
4+3>6
∴能组成三角形
判断三条线段能否组成三角形的方法:
①找出最长线段.
②比较较短两边之和与最长线段的大小
③判断能否组成三角形.
知识点2 三角形的三边关系
练一练 1.下列长度的三条线段能否组成三角形?
(1) 3,8,4
(2) 2,5,6
(3) 5,6,10
(4) 3,5,8
不能
能
能
不能
知识点2 三角形的三边关系
已知一个三角形的最小边为2cm,另两边分别为6cm和a cm , a的取值范围是什么?
知识点2 三角形的三边关系
大家谈谈:观察下图中的三角形,试着比较它们之间的不同之处.
提示:可根据三角形三边的长度关系进行比较
不等边三角形
(三条边长度均不相等)
等腰三角形
(两条边长度相等)
等边三角形
(三条边长相等)
顶角
底角
腰
底边
知识点3 三角形按边分类
归纳:三条边各不相等的三角形叫做不等边三角形;
有两条边相等的三角形叫做等腰三角形;
三条边都相等的三角形叫做等边三角形 .
等腰三角形与等边三角形的关系:
等边三角形是特殊的等边三角形,即底边和腰相等的 等腰三角形.
知识点3 三角形按边分类
三角形进行分类
两边相等的等腰三角形
三边相等的等腰三角形
等边三角形
三角形
等腰三角形
三边不等的三角形
按边分
不等边三角形
三角形
三边都不相等的三角形
等腰三角形
等边三角形
知识点3 三角形按边分类
1. [2024廊坊校级月考] 下面是四位同学分别用三根木棍组成
的图形,其中是三角形的是( )
A
A. B. C. D.
返回
2. 如图,以 为边的三角形有( )
D
(第2题)
A. 1个 B. 2个 C. 3个 D. 4个
返回
3. 教材P128练习T3 满足下列条件的三条线段,, ,
能构成三角形的是( )
C
A. B. ,
C. ,, D. ,
返回
(第4题)
4. [2024邢台校级期中] 如图表示的是三角形的
分类,则下列说法正确的是( )
C
A. 表示等边三角形
B. 表示锐角三角形
C. 表示等腰三角形
D. 表示三边都不相等的三角形
返回
5. 绝缘梯是电力工程的专用登高
工具,如图,在绝缘梯示意图中,, 的长
度都为,则, 两点之间的距离可能是
( )
A
A. B. C. D.
返回
6.如图,图中有___个三角形,含 的三角形为___________
______________,在中,的对角是_______, 的
对边是____.
6
,,
返回
7. 已知一个三角形的三条边的长分别为
,, .若这个三角形是等腰三角形,求它的三边
的长.
【解】
需分两种情况讨论:
①若,则 ,此时三边长分别为3,3,7,不
能构成三角形,舍去;
②若,则 ,此时三边长分别为5,9,9,能
构成三角形,符合题意.
综上,当这个三角形是等腰三角形时,三边长分别为5,9,9.
返回
8. [2024秦皇岛期末] 若使用如图所示的①、②两根直铁丝做
成一个三角形框架,则需要将其中一根铁丝分为两段,则下
列说法正确的是( )
C
A. ①②都可以分为两段 B. ①②都不可以分为两段
C. 只有①可以分为两段 D. 只有②可以分为两段
返回
三角形
概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
分类
不等边三角形
等腰三角形(包括等边三角形)
三边关系
任意两边之和大于第三边
谢谢观看!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
