人教版八年级数学下册 18.2.1矩形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册 18.2.1矩形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 321.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 00:00:00 | ||
图片预览



文档简介
18.2.1矩形
一、单选题
1.矩形具有而平行四边形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行 D.对角相等
2.如图,在四边形ABCD中,对角线AC、BD相交于点O,OA=OC,OB=OD,添加下列条件,不能判定四边形ABCD是矩形的是( )
A.AB=AD B.OA=OB C.AB⊥AD D.∠ABO=∠BAO
3.如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断正确的是( )
A.四边形ABCD由矩形变为菱形
B.对角线AC的长度不变
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变
4.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12 B.10 C.7.5 D.5
5.下列性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都是是直角
C.对角线互相垂直 D.是轴对称图形
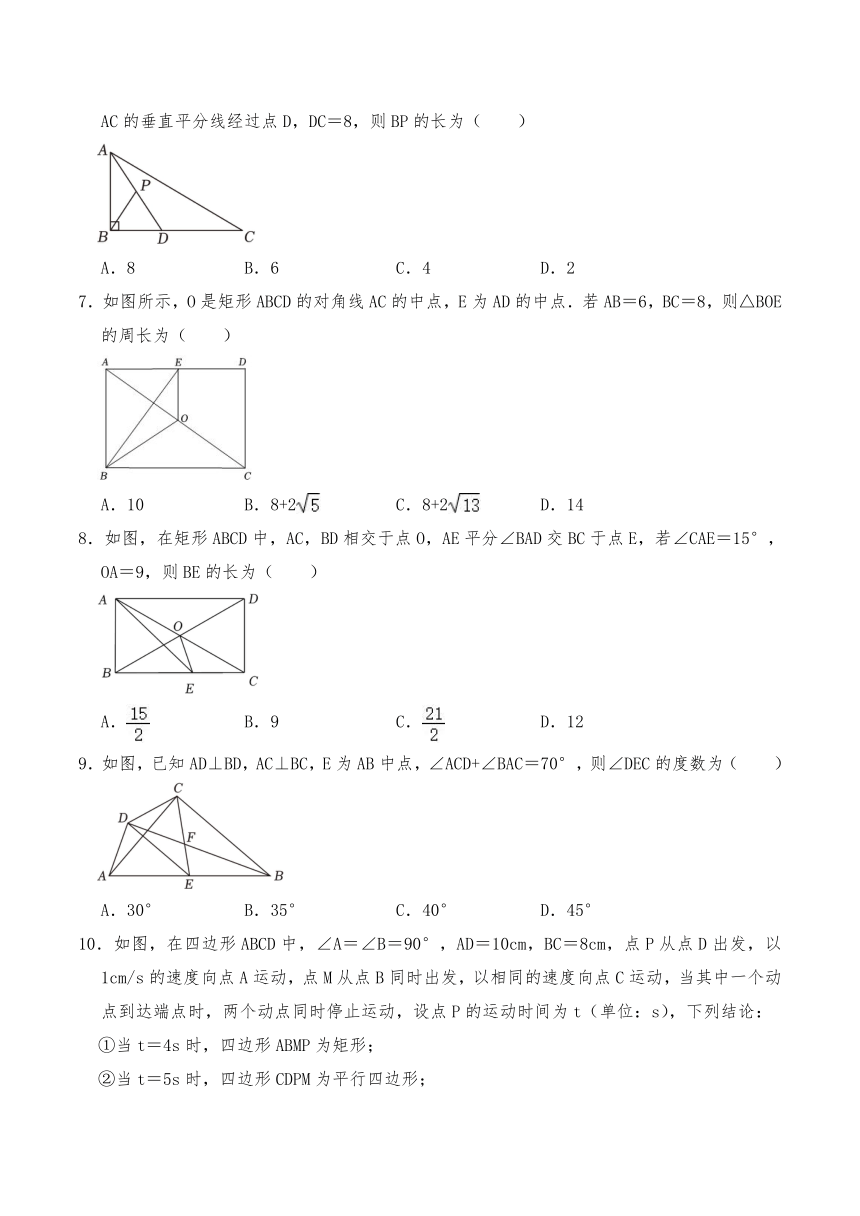
6.如图,在△ABC中,∠ABC=90°,点D是边BC上一点,连接AD,点P是AD的中点,若AC的垂直平分线经过点D,DC=8,则BP的长为( )
A.8 B.6 C.4 D.2
7.如图所示,O是矩形ABCD的对角线AC的中点,E为AD的中点.若AB=6,BC=8,则△BOE的周长为( )
A.10 B.8+2 C.8+2 D.14
8.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,OA=9,则BE的长为( )
A. B.9 C. D.12
9.如图,已知AD⊥BD,AC⊥BC,E为AB中点,∠ACD+∠BAC=70°,则∠DEC的度数为( )
A.30° B.35° C.40° D.45°
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动,设点P的运动时间为t(单位:s),下列结论:
①当t=4s时,四边形ABMP为矩形;
②当t=5s时,四边形CDPM为平行四边形;
③当CD=PM时,t=4或5s;
④当CD=PM时,t=4或6s.
其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,公路AC与BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AC的长为6km,BC的长为8km,则C,M两点间的距离为 km.
12.如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足分别为E、F.求PE+PF= .
13.如图,P是Rt△ABC的斜边AC(不与点A、C重合)上一动点,分别作PM⊥AB于点M,PN⊥BC于点N,O是MN的中点,若AB=5,BC=12,当点P在AC上运动时,BO的最小值是 .
14.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为 .
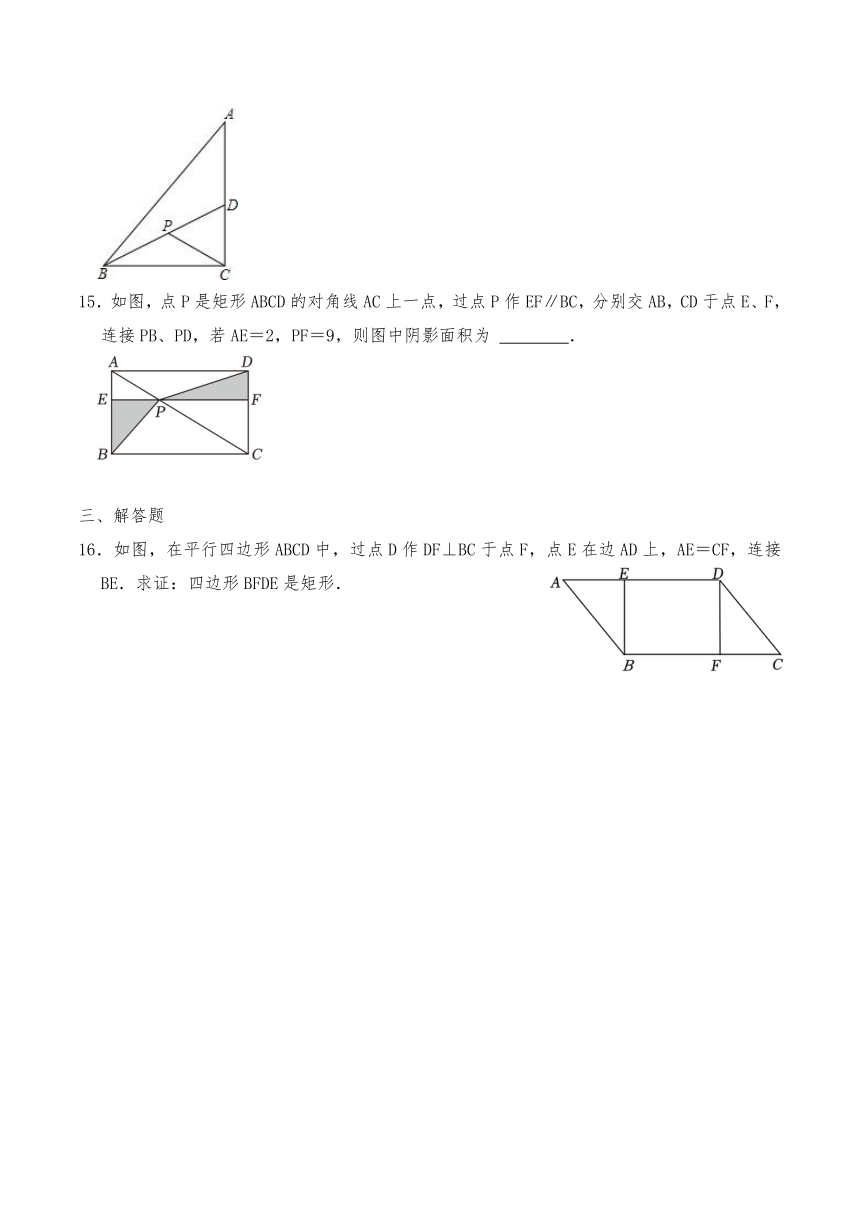
15.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E、F,连接PB、PD,若AE=2,PF=9,则图中阴影面积为 .
三、解答题
16.如图,在平行四边形ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连接BE.求证:四边形BFDE是矩形.
17.课本在线
想一想
我们知道,矩形的四个角都是直角.反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?请证明你的结论,并与同伴交流.
定理:有三个角是直角的四边形是矩形.
定理证明
为了证明该定理,小丽同学画出了图形(如图),写出了“已知”,请你补出“求证”的内容,并根据她的思路补全证明过程.
已知:如图,四边形ABCD中,∠A=∠B=∠C=90°.
求证: .
证明:∵∠A=∠B=90°,
∴∠A+∠B= °.
∴AD∥BC( ).
又∵∠B=∠C=90°,
∴ .
∴AB∥CD.
∴四边形ABCD是平行四边形( ).
又∵∠B=90°,
∴ ABCD是矩形( ).
18.如图,在 ABCD中,DE平分∠ADB,交AB于点E,BF平分∠CBD,交CD于点F.
(1)求证:DE=BF;
(2)若AD=BD,求证:四边形DEBF是矩形.
19.如图,在△ABC中,BD、CE分别是边AC、AB上的高线,取F为BC中点,连接点D,E,F得到△DEF,G是ED中点.
(1)求证:FG⊥DE;
(2)如果∠A=60°,BC=16,求FG的长度.
20.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)用含有t的代数式表示EF的长.
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,直接写出当t为何值时,四边形EGFH为矩形.
21.如图,已知等腰△ABC,AB=AC,点D是边BC的中点,AE是外角∠FAC的平分线,过点C作CE⊥AE,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)连接DE,若矩形ADCE的周长是28,DE=10,求四边形ABDE的面积.
答案
一、单选题
1.
【解答】解:矩形的性质:对边平行且相等,对角线互相平分且相等,两组对角相等;
平行四边形的性质:对边平行且相等,对角线互相平分,两组对角相等;
故选项B、C、D不符合题意,A符合题意;
故选:A.
2.
【解答】解:∵四边形ABCD中,OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
当AB=AD时,可判定四边形ABCD是菱形;
当AB⊥AD时,可判定四边形ABCD是矩形;
当OA=OB时,AC=BD,可判定四边形ABCD是矩形;
当∠BAO=∠ABO时,
∴OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
故选:A.
3.
【解答】解:向左扭动矩形框架ABCD,只改变四边形的形状,四边形变成平行四边形,A不符合题意;
此时对角线BD减小,对角线AC增大,B不合题意.
BC边上的高减小,故面积变小,C不符合题意,
四边形的四条边不变,故周长不变,D符合题意.
故选:D.
4.
【解答】解:如图所示:矩形ABCD,对角线AC=BD=15,∠AOD=∠BOC=60°
∵四边形ABCD是矩形
∴OA=OD=OC=OB=×15=7.5(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=7.5,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为7.5,
故选:C.
5.
【解答】解:A、矩形的对角线平分、相等,故A正确,不合题意;
B、矩形的四个角都是直角,故B正确,不合题意;
C、矩形的对角线不互相垂直,故C错误,符合题意;
D、矩形是轴对称图形,故D正确,不合题意;
故选:C.
6.
【解答】解:∵点D在AC的垂直平分线上,
∴DA=DC=8,
∵∠ABC=90°,点P是AD的中点,
∴BP=AD=4,
故选:C.
7.
【解答】解:∵四边形ABCD是矩形,AB=6,BC=8,
∴AB=CD=6,AD=BC=8,
∵点O是AC的中点,E为AD的中点,
∴OE=CD=3,AE=AD=4,
在Rt△ABE中,AE=4,AB=6,
根据勾股定理得,BE=,
在Rt△ABC中,根据勾股定理得,
AC===10.
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵点O是AC的中点,
∴BO=5.
∴△BOE周长为5+3+2=8+2.
故选:C.
8.
【解答】解:在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠EAD=45°,AD∥BC,OA=OB=6,
∴∠AEB=∠EAD=45°,
∴BE=BA.
∵∠CAE=15°,∠BAE=45°,
∴∠BAC=60°,
又∵OA=OB,
∴△OAB为等边三角形,
∴BO=BA=9,
∴BO=BE=9.
故选:B.
9.
【解答】解:∵AD⊥BD,AC⊥BC,
∴△ABD,△ABC均为直角三角形,
∵E为AB中点,
∴CE=AB,
∴CE=AE=BE=DE,
∴∠ACE=∠BAC,∠DCE=∠EDC,
∵∠ACD+∠BAC=70°,
∴∠DCE=∠EDC=70°,
∴∠DEC=180°﹣∠DCE﹣∠EDC=180°﹣70°﹣70°=40°.
故选:C.
10.
【解答】解:根据题意,可得DP=t cm,BM=t cm,
∵AD=10cm,BC=8cm,
∴AP=(10﹣t)cm,CM=(8﹣t)cm,
当四边形ABMP为矩形时,AP=BM,
即10﹣t=t,解得t=5,故①不正确;
当四边形CDPM为平行四边形时,则DP=CM,
即8﹣t=t,解得t=4,故②不正确;
当CD=PM时,分两种情况:
当四边形CDPM是平行四边形时,则DP=CM,
即8﹣t=t,解得t=4,
当四边形CDPM是等腰梯形时,
过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示,
则∠MGP=∠CHD=90°,
∵CD=PM,GM=HC,
∴Rt△MGP≌Rt△CHD(HL),
∴GP=HD,
∴,
又BM=t,∠A=∠B=90°,MG⊥AD,
∴AG=BM,
即,
解得t=6,
综上可得,当CD=PM时,
t=6或t=4,
故③错误,④正确,
∴正确的结论有1个.
故选:A.
二、填空题
11.
【解答】解:∵公路AC与BC互相垂直,AC的长为6km,BC的长为8km,
∴AB===10(km),
∵点M是线段AB的中点,
∴CM=AB=5(km).
故答案为:5.
12.
【解答】解:连接OP,如图所示:
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB BC=12,OA=OC,OB=OD,AC=BD,AC==5,
∴S△AOD=S矩形ABCD=3,OA=OD=,
∴S△AOD=S△AOP+S△DOP=OA PE+OD PF=OA(PE+PF)=×(PE+PF)=3,
∴PE+PF=,
故答案为:.
13.
【解答】解:连接BP,如图所示:
∵∠ABC=90°,PM⊥AB于点M,PN⊥BC于点N,
∴∠ABC=∠PMB=∠PNB=90°,
∴四边形BMPN是矩形,AC===13,
∴BP=MN,BP与MN互相平分,
∵点O是MN的中点,
∴点O是BP的中点,
∴BO=BP=MN,
当BP⊥AC时,BP最小===,
∴MN=,
∴BO的最小值=MN=,
故答案为:.
14.
【解答】解:如图,过点D作DE⊥AB于E,
∵∠ACB=90°,∠ABC=60°,
∴∠A=90°﹣60°=30°,
∴DE=AD=×6=3,
又∵BD平分∠ABC,
∴CD=DE=3,
∵∠ABC=60°,BD平分∠ABC,
∴∠CBD=30°,
∴BD=2CD=2×3=6,
∵P点是BD的中点,
∴CP=BD=×6=3.
故答案为:3.
15.
【解答】解:过点P作GH分别交AD、BC于点G、H,
由矩形性质可知,
S△ADC=S△ABC,S△PFC=S△PHC,S△AGP=S△AEP,
∴S△ADC﹣S△PFC﹣S△AGP=S△ABC﹣S△PHC﹣S△AEP,
即S四边形GPFD=S四边形EPHB,
∴S四边形GPFD=S四边形EPHB,即S△DPF=S△PEB.
∵GP=AE=2,PF=9,
∴S△DPF==9=S△PEB.
即图中阴影面积为S△DPF+S△PEB=9+9=18.
故答案为:18.
三、解答题
16.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵ED=AD﹣AE,BF=BC﹣CF,AE=CF,
∴ED=BF,
∴四边形BFDE是平行四边形,
又∵DF⊥BC,
∴∠DFB=90°,
∴平行四边形BFDE是矩形.
17.解:求证:四边形ABCD是矩形.
证明:∵∠A=∠B=90°,
∴∠A+∠B=180°.
∴AD∥BC( 同旁内角互补,两直线平行).
又∵∠B=∠C=90°,
∴∠B+∠C=180°.
∴AB∥CD.
∴四边形ABCD是平行四边形( 两组对边分别平行的四边形是平行四边形).
又∵∠B=90°,
∴ ABCD是矩形( 有一个角为直角的平行四边形是矩形).
故答案为:四边形ABCD是矩形;180;同旁内角互补,两直线平行;∠B+∠C=180°;两组对边分别平行的四边形是平行四边形;有一个角为直角的平行四边形是矩形.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADB=∠CBD,
∵DE平分∠ADB,BF平分∠CBD,
∴∠EDB=∠ADB,∠DBF=∠CBD,
∴∠EDB=∠DBF,
∴DE∥BF,
又∵AB∥CD,
∴四边形DEBF是平行四边形.
∴DE=BF.
(2)∵AD=BD,DE平分∠ADB,
∴DE⊥AB,
又∵四边形DEBF是平行四边形,
∴四边形DEBF是矩形.
19.(1)证明:在△ABC中,BD、CE分别是边AC、AB上的高线,
∴∠BDC=∠CEB=90°,
∵F是BC的中点,
∴EF=DF=BC,
∴△DEF是等腰三角形,
∵G是ED的中点,
∴FG⊥DE;
(2)解:∵BD、CE分别是边AC、AB上的高线.
∴∠BDC=∠CEB=90°,
∵F是BC的中点,BC=16,
∴EF=DF=BC=BF=CF=8,
∴∠BEF=∠ABC,∠CDF=∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴∠BFE+∠CFD=360°﹣2(∠ABC+∠ACB)=120°,
∴∠EFD=60°,
∴△DEF是等边三角形,
∵G是ED的中点,
∴EG=DE=EF=4,
∴FG===4.
20.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC===5,
由题意得:AE=CF=t,
∴EF相遇前为:EF=AC﹣AE﹣CF=5﹣2t;
EF相遇后为:EF=AE+CF﹣AC=2t﹣5;
故答案为:5﹣2t或2t﹣5;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC===5,∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,
,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形;
(3)解:如图所示,连接GH,
由(2)可知四边形EGFH是平行四边形
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4,
解得:t=0.5.
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5,
即:当t为0.5或4.5时,四边形EGFH为矩形.
21.(1)证明:∵AB=AC,点D是边BC的中点,
∴∠BAD=∠CAD,AD⊥BC,
∴∠ADC=90°,
∵AE是∠FAC的平分线,
∴∠FAE=∠CAE,
∵∠BAD+∠CAD+∠FAE+∠CAE=180°,
∴∠CAD+∠CAE=×180°=90°,
即∠DAE=90°,
∵CE⊥AE,
∴∠ADC=∠AEC=∠DAE=90°,
∴四边形ADCE是矩形;
(2)解:如图,∵四边形ADCE是矩形,
∴∠AC=90°,DE=AC=15,AE∥BD,AE=CD,
∵点D是边BC的中点,
∴BD=CD,
∴AE=BD,
∴四边形ABDE是平行四边形,
∵矩形ADCE的周长是28,
∴AD+CD=14,
∴(AD+CD)2=142,
即AD2+CD2+2AD CD=142,
∵AD2+CD2=AC2=102,
∴AD CD==48,
∴AD BD=48,
∴S平行四边形ABDE=BD AD=48.
一、单选题
1.矩形具有而平行四边形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行 D.对角相等
2.如图,在四边形ABCD中,对角线AC、BD相交于点O,OA=OC,OB=OD,添加下列条件,不能判定四边形ABCD是矩形的是( )
A.AB=AD B.OA=OB C.AB⊥AD D.∠ABO=∠BAO
3.如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断正确的是( )
A.四边形ABCD由矩形变为菱形
B.对角线AC的长度不变
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变
4.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12 B.10 C.7.5 D.5
5.下列性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都是是直角
C.对角线互相垂直 D.是轴对称图形
6.如图,在△ABC中,∠ABC=90°,点D是边BC上一点,连接AD,点P是AD的中点,若AC的垂直平分线经过点D,DC=8,则BP的长为( )
A.8 B.6 C.4 D.2
7.如图所示,O是矩形ABCD的对角线AC的中点,E为AD的中点.若AB=6,BC=8,则△BOE的周长为( )
A.10 B.8+2 C.8+2 D.14
8.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,OA=9,则BE的长为( )
A. B.9 C. D.12
9.如图,已知AD⊥BD,AC⊥BC,E为AB中点,∠ACD+∠BAC=70°,则∠DEC的度数为( )
A.30° B.35° C.40° D.45°
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动,设点P的运动时间为t(单位:s),下列结论:
①当t=4s时,四边形ABMP为矩形;
②当t=5s时,四边形CDPM为平行四边形;
③当CD=PM时,t=4或5s;
④当CD=PM时,t=4或6s.
其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,公路AC与BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AC的长为6km,BC的长为8km,则C,M两点间的距离为 km.
12.如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足分别为E、F.求PE+PF= .
13.如图,P是Rt△ABC的斜边AC(不与点A、C重合)上一动点,分别作PM⊥AB于点M,PN⊥BC于点N,O是MN的中点,若AB=5,BC=12,当点P在AC上运动时,BO的最小值是 .
14.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为 .
15.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E、F,连接PB、PD,若AE=2,PF=9,则图中阴影面积为 .
三、解答题
16.如图,在平行四边形ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连接BE.求证:四边形BFDE是矩形.
17.课本在线
想一想
我们知道,矩形的四个角都是直角.反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?请证明你的结论,并与同伴交流.
定理:有三个角是直角的四边形是矩形.
定理证明
为了证明该定理,小丽同学画出了图形(如图),写出了“已知”,请你补出“求证”的内容,并根据她的思路补全证明过程.
已知:如图,四边形ABCD中,∠A=∠B=∠C=90°.
求证: .
证明:∵∠A=∠B=90°,
∴∠A+∠B= °.
∴AD∥BC( ).
又∵∠B=∠C=90°,
∴ .
∴AB∥CD.
∴四边形ABCD是平行四边形( ).
又∵∠B=90°,
∴ ABCD是矩形( ).
18.如图,在 ABCD中,DE平分∠ADB,交AB于点E,BF平分∠CBD,交CD于点F.
(1)求证:DE=BF;
(2)若AD=BD,求证:四边形DEBF是矩形.
19.如图,在△ABC中,BD、CE分别是边AC、AB上的高线,取F为BC中点,连接点D,E,F得到△DEF,G是ED中点.
(1)求证:FG⊥DE;
(2)如果∠A=60°,BC=16,求FG的长度.
20.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)用含有t的代数式表示EF的长.
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,直接写出当t为何值时,四边形EGFH为矩形.
21.如图,已知等腰△ABC,AB=AC,点D是边BC的中点,AE是外角∠FAC的平分线,过点C作CE⊥AE,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)连接DE,若矩形ADCE的周长是28,DE=10,求四边形ABDE的面积.
答案
一、单选题
1.
【解答】解:矩形的性质:对边平行且相等,对角线互相平分且相等,两组对角相等;
平行四边形的性质:对边平行且相等,对角线互相平分,两组对角相等;
故选项B、C、D不符合题意,A符合题意;
故选:A.
2.
【解答】解:∵四边形ABCD中,OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
当AB=AD时,可判定四边形ABCD是菱形;
当AB⊥AD时,可判定四边形ABCD是矩形;
当OA=OB时,AC=BD,可判定四边形ABCD是矩形;
当∠BAO=∠ABO时,
∴OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
故选:A.
3.
【解答】解:向左扭动矩形框架ABCD,只改变四边形的形状,四边形变成平行四边形,A不符合题意;
此时对角线BD减小,对角线AC增大,B不合题意.
BC边上的高减小,故面积变小,C不符合题意,
四边形的四条边不变,故周长不变,D符合题意.
故选:D.
4.
【解答】解:如图所示:矩形ABCD,对角线AC=BD=15,∠AOD=∠BOC=60°
∵四边形ABCD是矩形
∴OA=OD=OC=OB=×15=7.5(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=7.5,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为7.5,
故选:C.
5.
【解答】解:A、矩形的对角线平分、相等,故A正确,不合题意;
B、矩形的四个角都是直角,故B正确,不合题意;
C、矩形的对角线不互相垂直,故C错误,符合题意;
D、矩形是轴对称图形,故D正确,不合题意;
故选:C.
6.
【解答】解:∵点D在AC的垂直平分线上,
∴DA=DC=8,
∵∠ABC=90°,点P是AD的中点,
∴BP=AD=4,
故选:C.
7.
【解答】解:∵四边形ABCD是矩形,AB=6,BC=8,
∴AB=CD=6,AD=BC=8,
∵点O是AC的中点,E为AD的中点,
∴OE=CD=3,AE=AD=4,
在Rt△ABE中,AE=4,AB=6,
根据勾股定理得,BE=,
在Rt△ABC中,根据勾股定理得,
AC===10.
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵点O是AC的中点,
∴BO=5.
∴△BOE周长为5+3+2=8+2.
故选:C.
8.
【解答】解:在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠EAD=45°,AD∥BC,OA=OB=6,
∴∠AEB=∠EAD=45°,
∴BE=BA.
∵∠CAE=15°,∠BAE=45°,
∴∠BAC=60°,
又∵OA=OB,
∴△OAB为等边三角形,
∴BO=BA=9,
∴BO=BE=9.
故选:B.
9.
【解答】解:∵AD⊥BD,AC⊥BC,
∴△ABD,△ABC均为直角三角形,
∵E为AB中点,
∴CE=AB,
∴CE=AE=BE=DE,
∴∠ACE=∠BAC,∠DCE=∠EDC,
∵∠ACD+∠BAC=70°,
∴∠DCE=∠EDC=70°,
∴∠DEC=180°﹣∠DCE﹣∠EDC=180°﹣70°﹣70°=40°.
故选:C.
10.
【解答】解:根据题意,可得DP=t cm,BM=t cm,
∵AD=10cm,BC=8cm,
∴AP=(10﹣t)cm,CM=(8﹣t)cm,
当四边形ABMP为矩形时,AP=BM,
即10﹣t=t,解得t=5,故①不正确;
当四边形CDPM为平行四边形时,则DP=CM,
即8﹣t=t,解得t=4,故②不正确;
当CD=PM时,分两种情况:
当四边形CDPM是平行四边形时,则DP=CM,
即8﹣t=t,解得t=4,
当四边形CDPM是等腰梯形时,
过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示,
则∠MGP=∠CHD=90°,
∵CD=PM,GM=HC,
∴Rt△MGP≌Rt△CHD(HL),
∴GP=HD,
∴,
又BM=t,∠A=∠B=90°,MG⊥AD,
∴AG=BM,
即,
解得t=6,
综上可得,当CD=PM时,
t=6或t=4,
故③错误,④正确,
∴正确的结论有1个.
故选:A.
二、填空题
11.
【解答】解:∵公路AC与BC互相垂直,AC的长为6km,BC的长为8km,
∴AB===10(km),
∵点M是线段AB的中点,
∴CM=AB=5(km).
故答案为:5.
12.
【解答】解:连接OP,如图所示:
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB BC=12,OA=OC,OB=OD,AC=BD,AC==5,
∴S△AOD=S矩形ABCD=3,OA=OD=,
∴S△AOD=S△AOP+S△DOP=OA PE+OD PF=OA(PE+PF)=×(PE+PF)=3,
∴PE+PF=,
故答案为:.
13.
【解答】解:连接BP,如图所示:
∵∠ABC=90°,PM⊥AB于点M,PN⊥BC于点N,
∴∠ABC=∠PMB=∠PNB=90°,
∴四边形BMPN是矩形,AC===13,
∴BP=MN,BP与MN互相平分,
∵点O是MN的中点,
∴点O是BP的中点,
∴BO=BP=MN,
当BP⊥AC时,BP最小===,
∴MN=,
∴BO的最小值=MN=,
故答案为:.
14.
【解答】解:如图,过点D作DE⊥AB于E,
∵∠ACB=90°,∠ABC=60°,
∴∠A=90°﹣60°=30°,
∴DE=AD=×6=3,
又∵BD平分∠ABC,
∴CD=DE=3,
∵∠ABC=60°,BD平分∠ABC,
∴∠CBD=30°,
∴BD=2CD=2×3=6,
∵P点是BD的中点,
∴CP=BD=×6=3.
故答案为:3.
15.
【解答】解:过点P作GH分别交AD、BC于点G、H,
由矩形性质可知,
S△ADC=S△ABC,S△PFC=S△PHC,S△AGP=S△AEP,
∴S△ADC﹣S△PFC﹣S△AGP=S△ABC﹣S△PHC﹣S△AEP,
即S四边形GPFD=S四边形EPHB,
∴S四边形GPFD=S四边形EPHB,即S△DPF=S△PEB.
∵GP=AE=2,PF=9,
∴S△DPF==9=S△PEB.
即图中阴影面积为S△DPF+S△PEB=9+9=18.
故答案为:18.
三、解答题
16.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵ED=AD﹣AE,BF=BC﹣CF,AE=CF,
∴ED=BF,
∴四边形BFDE是平行四边形,
又∵DF⊥BC,
∴∠DFB=90°,
∴平行四边形BFDE是矩形.
17.解:求证:四边形ABCD是矩形.
证明:∵∠A=∠B=90°,
∴∠A+∠B=180°.
∴AD∥BC( 同旁内角互补,两直线平行).
又∵∠B=∠C=90°,
∴∠B+∠C=180°.
∴AB∥CD.
∴四边形ABCD是平行四边形( 两组对边分别平行的四边形是平行四边形).
又∵∠B=90°,
∴ ABCD是矩形( 有一个角为直角的平行四边形是矩形).
故答案为:四边形ABCD是矩形;180;同旁内角互补,两直线平行;∠B+∠C=180°;两组对边分别平行的四边形是平行四边形;有一个角为直角的平行四边形是矩形.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADB=∠CBD,
∵DE平分∠ADB,BF平分∠CBD,
∴∠EDB=∠ADB,∠DBF=∠CBD,
∴∠EDB=∠DBF,
∴DE∥BF,
又∵AB∥CD,
∴四边形DEBF是平行四边形.
∴DE=BF.
(2)∵AD=BD,DE平分∠ADB,
∴DE⊥AB,
又∵四边形DEBF是平行四边形,
∴四边形DEBF是矩形.
19.(1)证明:在△ABC中,BD、CE分别是边AC、AB上的高线,
∴∠BDC=∠CEB=90°,
∵F是BC的中点,
∴EF=DF=BC,
∴△DEF是等腰三角形,
∵G是ED的中点,
∴FG⊥DE;
(2)解:∵BD、CE分别是边AC、AB上的高线.
∴∠BDC=∠CEB=90°,
∵F是BC的中点,BC=16,
∴EF=DF=BC=BF=CF=8,
∴∠BEF=∠ABC,∠CDF=∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴∠BFE+∠CFD=360°﹣2(∠ABC+∠ACB)=120°,
∴∠EFD=60°,
∴△DEF是等边三角形,
∵G是ED的中点,
∴EG=DE=EF=4,
∴FG===4.
20.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC===5,
由题意得:AE=CF=t,
∴EF相遇前为:EF=AC﹣AE﹣CF=5﹣2t;
EF相遇后为:EF=AE+CF﹣AC=2t﹣5;
故答案为:5﹣2t或2t﹣5;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC===5,∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,
,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形;
(3)解:如图所示,连接GH,
由(2)可知四边形EGFH是平行四边形
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4,
解得:t=0.5.
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5,
即:当t为0.5或4.5时,四边形EGFH为矩形.
21.(1)证明:∵AB=AC,点D是边BC的中点,
∴∠BAD=∠CAD,AD⊥BC,
∴∠ADC=90°,
∵AE是∠FAC的平分线,
∴∠FAE=∠CAE,
∵∠BAD+∠CAD+∠FAE+∠CAE=180°,
∴∠CAD+∠CAE=×180°=90°,
即∠DAE=90°,
∵CE⊥AE,
∴∠ADC=∠AEC=∠DAE=90°,
∴四边形ADCE是矩形;
(2)解:如图,∵四边形ADCE是矩形,
∴∠AC=90°,DE=AC=15,AE∥BD,AE=CD,
∵点D是边BC的中点,
∴BD=CD,
∴AE=BD,
∴四边形ABDE是平行四边形,
∵矩形ADCE的周长是28,
∴AD+CD=14,
∴(AD+CD)2=142,
即AD2+CD2+2AD CD=142,
∵AD2+CD2=AC2=102,
∴AD CD==48,
∴AD BD=48,
∴S平行四边形ABDE=BD AD=48.
