人教版八年级数学下册 18.2.2菱形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册 18.2.2菱形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 488.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 10:49:54 | ||
图片预览




文档简介
18.2.2菱形
一、单选题
1.下列选项中,菱形不具有的性质是( )
A.四边相等
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
2.在四边形ABCD中,AD=BC,AB=CD.下列说法能使四边形ABCD为菱形的是( )
A.AC=BD B.∠C=∠D C.∠A=∠B D.AC⊥BD
3.如图,在菱形ABCD中,对角线AC、BD交于点F,E是AB的中点,若EF=2,则菱形ABCD的边长是( )
A.2 B.4 C.6 D.8
4.如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=3,DB=4,则点A到BC的距离为( )
A. B. C. D.
5.如图,在菱形ABCD中,对角线AC和BD相交于点O,若AC=6,BD=2,则菱形ABCD的周长为( )
A.24 B.8 C. D.
6.如图,菱形ABCD,∠B=60°,E,F分别是CB,CD上两点,连接AE,AF,EF,且∠EAF=60°,如果∠BAE=α,则下列说法错误的是( )
A.∠CEF=α B.∠FAD=60°﹣α
C.∠EFC=60°﹣α D.∠AFD=90°﹣α
7.如图,在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=120°,BD=4,则对角线AC的长为( )
A. B. C.4 D.8
8.如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,在条件:①AB=AD;②AC=BD;③AC⊥BD;④AC平分∠BAD中,选择一个条件,使得四边形ABCD是菱形,可选择的条件是( )
A.①②③ B.①②④ C.①③④ D.②③④
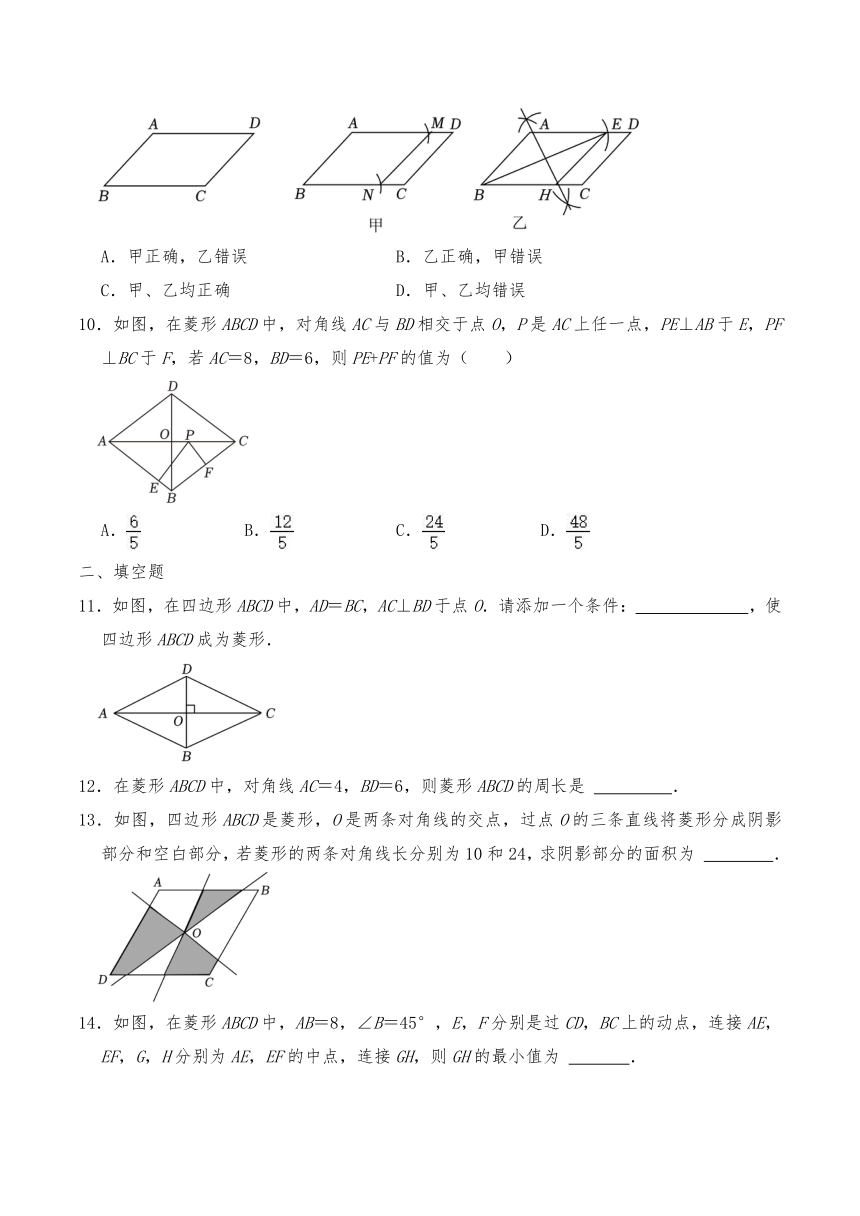
9.如图,在给定的平行四边形上,作一个菱形,甲、乙二人的做法如下:
甲:分别以A、B为圆心,AB长为半径画弧,交AD于点M,交BC于点N,连接MN,则四边形ABNM为菱形;
乙:以A为圆心,AB长为半径画弧,交AD于点E,连接BE,作BE的垂直平分线交BC于点H,则四边形ABHE为菱形;
根据两人的做法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
10.如图,在菱形ABCD中,对角线AC与BD相交于点O,P是AC上任一点,PE⊥AB于E,PF⊥BC于F,若AC=8,BD=6,则PE+PF的值为( )
A. B. C. D.
二、填空题
11.如图,在四边形ABCD中,AD=BC,AC⊥BD于点O.请添加一个条件: ,使四边形ABCD成为菱形.
12.在菱形ABCD中,对角线AC=4,BD=6,则菱形ABCD的周长是 .
13.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影部分和空白部分,若菱形的两条对角线长分别为10和24,求阴影部分的面积为 .
14.如图,在菱形ABCD中,AB=8,∠B=45°,E,F分别是过CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH,则GH的最小值为 .
15.如图,菱形ABCD的边长为26,对角线AC的长为48,延长AB至E,BF平分∠CBE,点G是BF上任意一点,则△ACG的面积为 .
三、解答题
16.如图,AD是△ABC的角平分线,AD的垂直平分线分别交AB、AC于点E、F,连接DE、DF.
(1)判断四边形AEDF的形状,并证明;
(2)当AB=9,AC=6时,求DF的长.
17.如图,在直角△AEC中,∠AEC=90°,B是边AE上一点,连接BC,O为AC的中点,过C作CD∥AB交BO延长线于D,且AC平分∠BCD,连接AD.
(1)求证:四边形ABCD是菱形.
(2)连接OE交BC于F,∠ACD=27°,求∠CFO的度数.
18.如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.
(1)求证:四边形AECD为菱形;
(2)若∠CEB=60°,DC=4,求△ABC的面积.
19.如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.
(1)求证:四边形AECD是菱形;
(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.
20.在Rt△ABC中,∠ACB=90°点D是边AB上的一个动点,连接CD.作AE∥DC,CE∥AB,连接ED.
(1)如图1,当CD⊥AB时,求证:AC=ED;
(2)如图2,当D是AB的中点时,
①四边形ADCE的形状是 ;请说明理由.
②若AB=5,ED=4,则四边形ADCE的面积为 .
21.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,点F在AD上,且AF=AB,连接BF交AE于点G,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若BF=10,AB=10,求菱形ABEF的面积.
22.如图,在 ABCD中,对角线AC和BD相交于点O,AD=10,AC=16,BD=12.
①求证: ABCD是菱形;
②延长BC至点E,连接OE交CD于点F,若∠E=∠ACD.求的值.
23.如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
答案
一、单选题
1.
【解答】解:∵菱形不具有的性质是对角线相等,
∴选项C符合题意,
故选:C.
2.
【解答】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
A、∵AC=BD,
∴平行四边形ABCD为矩形,故选项A不符合题意;
B、由AB=CD,不能判定四边形ABCD为菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、∵AC⊥BD,
∴平行四边形ABCD为菱形,故选项D符合题意;
故选:D.
3.
【解答】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,
∴∠AFB=90°,
∵E为AB的中点,且EF=2,
∴AB=2EF=4,
即菱形ABCD的边长是4,
故选:B.
4.
【解答】解:∵四边形ABCD是菱形,
∴AC垂直平分BD,
∴BC==,菱形的面积为=6,
设点A到BC的距离为h,
∴×h=6,
解得h=,
∴点A到BC的距离为.
故选:C.
5.
【解答】解:∵四边形ABCD为菱形,AC=6,BD=2,
∴AB=BC=CD=DA,AC⊥BD,OB=OD=BD=1,OA=OC=AC=3,
在Rt△OAB中,由勾股定理得:AB===,
∴菱形ABCD的周长=4AB=4,
故选:D.
6.
【解答】解:连接AC,EF,
∵四边形ABCD是菱形,
∴AB=BC,AB∥CD.
∴∠B+∠BCD=180°.
∵∠B=60°,
∴△ABC是等边三角形,∠BCD=120°.
∴∠BAC=∠ACB=60°,AB=AC.
∴∠ACF=∠B=60°.∠CAD=60°,
∵∠EAF=60°,
∴∠BAC﹣∠CAE=∠EAF﹣∠CAE.
∴∠BAE=∠CAF=α.
∴△ABE≌△ACF(ASA).∠FAD=60°﹣α,
∴∠B=∠ACF=60°,AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∴∠AFE=60°,
∴△AEF是等边三角形,
∴∠AFE=60°,
∵∠AFC=∠FAD+∠D,
∴∠EFC=∠FAD=60°﹣α,
∴∠CEF=α,
不能证出∠AFD=90°﹣α,
故选:D.
7.
【解答】解:在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=120°,BD=4,
∴∠BAD=60°,AD=AB,
则△ABD是等边三角形,
∴AB=AD=CD=BC=4,∠DAC=BAD=30°,
故AO=4cos30°=2,
∴AC=2AO=4.
故选:A.
8.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADO=∠CBO,
∵点O是BD的中点,
∴OD=OB,
在△DAO和△BCO中,
,
∴△DAO≌△BCO(ASA),
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形,
①∵四边形ABCD是平行四边形,AB=AD,
∴平行四边形ABCD是菱形;
③∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形;
④∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAC=∠DCA,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴AD=CD,
∴平行四边形ABCD是菱形.
综上所述:选择①③④,使得四边形ABCD是菱形,
故选:C.
9.
【解答】解:甲:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
由作图可知,AM=AB,BN=AB,
∴AM=BN,
∴四边形ABNM是平行四边形,
∵AM=AB,
∴平行四边形ABNM为菱形,故甲的作法正确;
乙:如图,设AH交BE于点O,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠BHO,
∵AH垂直平分BE,
∴BO=EO,
又∵∠AOE=∠HOB,
∴△AOE≌△HOB(ASA),
∴AE=HB,
∴四边形ABHE为平行四边形,
又∵AE=AB,
∴平行四边形ABHE为菱形,故乙的作法正确;
故选:C.
10.
【解答】解:过P作PM⊥CD于M,
∵四边形ABCD是菱形,
∴CD∥AB,AC⊥BD,OA=AC,OB=BD,AC平分∠BCD,
∵PF⊥BC于F,
∴PF=PM,
∵PE⊥AB于,PM⊥CD,CD∥AB,
∴P、E、M共线,
∴PE+PF=PE+PM=ME,
∵AC=8,BD=6,
∴OA=×8=4,OB=×6=3,
∴AB==5,
∵菱形ABCD的面积=AB EM=AC BD,
∴5EM=×6×8,
∴EM=.
∴PE+PF的值为.
故选:C.
二、填空题
11.
【解答】解:当添加“AD∥BC”时,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
当添加:“AB=CD”时,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
当添加“OB=OD”时,
∵AD=BC,AC⊥BD,
∴Rt△ADO≌Rt△CBO(HL),
∴AO=CO,DO=BO,
∴四边形ABCD是菱形;
当添加:“∠ADB=∠CBD”时,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
故答案为:AD∥BC(或AB=CD或OB=OD 或ADB=∠CBD等 ).
12.
【解答】解:∵四边形ABCD是菱形,
∴菱形ABCD的边长==,
∴菱形ABCD的周长是4,
故答案为:4.
13.
【解答】解:∵菱形是中心对称图形,
∴由图得:阴影的面积等于菱形面积的一半,
∵菱形的两条对角线的长分别为10和24,
∴菱形的面积为×10×24=120,
∴阴影部分的面积为60,
故答案为:60.
14.
【解答】解:连接AF,如图所示:
∵四边形ABCD是菱形,
∴AB=BC=8,
∵G,H分别为AE,EF的中点,
∴GH是△AEF的中位线,
∴,
当AF⊥BC时,AF最小,GH得到最小值,
则∠AFB=90°,
∵∠B=45°,
∴△ABF是等腰直角三角形,
∴,
∴,
即GH的最小值为,
故答案为:.
15.
【解答】解:如图,连接BD交AC于点O,
∵四边形ABCD是菱形,
∴BD与AC互相垂直平分,
∴OA=OC=24,
∴OB=OD==10,
∵DA∥CB,
∴∠DAB=∠CBE,
∵AC平分∠DAB,
∴∠CAB=DAB,
∵BF平分∠CBE,
∴∠FBE=CBE,
∴∠CAB=∠FBE,
∴AC∥FB,
∴S△CBG=S△ABG,
∴S△ACG=S△ABC=×AC OB=×48×10=240,
则△ACG的面积为240.
故答案为:240.
三、解答题
16.解:(1)四边形AEDF是菱形,理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD,
又∵EF⊥AD,
∴∠AOE=∠AOF=90°
在△AEO和△AFO中,
,
∴△AEO≌△AFO(ASA),
∴EO=FO,
∵EF垂直平分AD,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形,
又EF⊥AD,
∴平行四边形AEDF为菱形;
(2)由(1)知四边形AEDF为菱形,
∴DF∥AB,DF=AF,
∴=,
∴=,
∵AB=9,AC=6,
即=,
解得:DF=.
17.(1)证明:∵CD∥AB,
∴∠OAB=∠OCD,
∵O为AC的中点,
∴OA=OC,
在△AOB和△OCD中,
,
∴△AOB≌△OCD(ASA),
∴OB=OD,
又∵OA=OC,
∴四边形ABCD是平行四边形,
∵CD∥AB,
∴∠BAC=∠DCA,
∵AC平分∠BCD,
∴∠BCA=∠DCA,
∴∠BAC=∠BCA,
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)解:∵CD∥AB,∠AEC=90°,
∴∠DCE+∠AEC=180°,
∴∠DCE=90°,
∴∠OCE=90°﹣∠ACD=90°﹣27°=63°,
由(1)可知,四边形ABCD是菱形,
∴∠ACB=∠ACD=27°,∠BCD=2∠ACD=54°,
∴∠ECF=90°﹣∠BCD=90°﹣54°=36°,
∵∠AEC=90°,OA=OC,
∴OE=AC=OC,
∴∠OEC=∠OCE=63°,
∴∠CFO=∠OEC+∠ECF=63°+36°=99°,
即∠CFO的度数为99°.
18.(1)证明:∵E为AB中点,
∴AB=2AE,
∵AB=2CD,
∴2AE=2CD,
∴AE=CD,
∵AB∥CD,
∴四边形AECD是平行四边形,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵∠DCA=∠BAC,
∴∠DAC=∠DCA,
∴DA=DC,
∴四边形AECD为菱形.
(2)解:∵AE=CE=DC=4,
∴AE=BE=CE=4,
∵∠CEB=60°,
∴△BCE是等边三角形,
∴∠BCE=60°,BC=BE=4,
∵∠ACE=∠CAE,
∴∠CEB=∠ACE+∠CAE=2∠ACE=60°,
∴∠ACE=30°,
∴∠ACB=∠ACE+∠BCE=30°+60°=90°,
∵AB=2AE=8,
∴AC===4,
∴S△ABC=BC AC=×4×4=8,
∴△ABC的面积为8.
19.(1)证明:∵AD=CD,BD⊥AC,
∴OA=OC,
∵OE=OD,
∴四边形AECD是平行四边形,
∵AC⊥BD,
∴平行四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴OE⊥OA,
∵CF⊥AE,AB平分∠EAC,
∴BF=OB,
∴Rt△AFB≌Rt△AOB(HL),
∴AF=OA=OC,
∵BF=OB=3,BE=5,
∴EF=,
∴OE=OB+BE=3+5=8,
∵∠EFB=∠AOE=90°,∠∠FEB=∠∠AEO,
∴△AEO∽△EBF,
∴,
即,
∴AE=10,
∴AD=AE=10.
20.(1)证明:∵AE∥DC,CE∥AB,
∴四边形ADCE是平行四边形,
∵CD⊥AB,
∴∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=ED.
(2)①解:∵AE∥DC,CE∥AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴AD=CD=BD,
∴四边形ADCE是菱形,
故答案为菱形;
②∵四边形ADCE是菱形,
∴AC⊥DE,
又∵AC⊥BC,
∴DE∥BC,
∵CE∥AB,
∴四边形ECBD是平行四边形,
∴DE=BC=4,
∵AB=5,
∴AC==3,
∴四边形ADCE的面积为.
故答案为6.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∵AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴平行四边形ABEF是菱形;
(2)解:∵四边形ABEF为菱形,
∴AF=AB=10,AG⊥BF,
又∵BF=10,
∴BG=FG=5,
∴=,
∴,
∴菱形ABEF的面积.
22.(1)证明:∵四边形ABCD是平行四边形,AC=16,BD=12,
∴AO=CO=AC=8,BO=DO=BD=6,
∵AD=10,
∴AO2+DO2=AD2,
∴△AOD是直角三角形,且∠AOD=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:如图,过点O作OG∥CD,交BC于点G,
则==1,
∴BG=CG,
由(1)可知, ABCD是菱形,
∴BC=AD=CD=10,∠ACD=∠ACB,
∴BG=CG=BC=5,
∵∠E=∠ACD,∠ACB=∠E+∠COE,
∴∠ACB=∠ACD=2∠E=∠E+∠COE,
∴∠E=∠COE,
∴OC=CE=8,
∵OG∥CD,
∴==.
23.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
一、单选题
1.下列选项中,菱形不具有的性质是( )
A.四边相等
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
2.在四边形ABCD中,AD=BC,AB=CD.下列说法能使四边形ABCD为菱形的是( )
A.AC=BD B.∠C=∠D C.∠A=∠B D.AC⊥BD
3.如图,在菱形ABCD中,对角线AC、BD交于点F,E是AB的中点,若EF=2,则菱形ABCD的边长是( )
A.2 B.4 C.6 D.8
4.如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=3,DB=4,则点A到BC的距离为( )
A. B. C. D.
5.如图,在菱形ABCD中,对角线AC和BD相交于点O,若AC=6,BD=2,则菱形ABCD的周长为( )
A.24 B.8 C. D.
6.如图,菱形ABCD,∠B=60°,E,F分别是CB,CD上两点,连接AE,AF,EF,且∠EAF=60°,如果∠BAE=α,则下列说法错误的是( )
A.∠CEF=α B.∠FAD=60°﹣α
C.∠EFC=60°﹣α D.∠AFD=90°﹣α
7.如图,在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=120°,BD=4,则对角线AC的长为( )
A. B. C.4 D.8
8.如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,在条件:①AB=AD;②AC=BD;③AC⊥BD;④AC平分∠BAD中,选择一个条件,使得四边形ABCD是菱形,可选择的条件是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.如图,在给定的平行四边形上,作一个菱形,甲、乙二人的做法如下:
甲:分别以A、B为圆心,AB长为半径画弧,交AD于点M,交BC于点N,连接MN,则四边形ABNM为菱形;
乙:以A为圆心,AB长为半径画弧,交AD于点E,连接BE,作BE的垂直平分线交BC于点H,则四边形ABHE为菱形;
根据两人的做法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
10.如图,在菱形ABCD中,对角线AC与BD相交于点O,P是AC上任一点,PE⊥AB于E,PF⊥BC于F,若AC=8,BD=6,则PE+PF的值为( )
A. B. C. D.
二、填空题
11.如图,在四边形ABCD中,AD=BC,AC⊥BD于点O.请添加一个条件: ,使四边形ABCD成为菱形.
12.在菱形ABCD中,对角线AC=4,BD=6,则菱形ABCD的周长是 .
13.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影部分和空白部分,若菱形的两条对角线长分别为10和24,求阴影部分的面积为 .
14.如图,在菱形ABCD中,AB=8,∠B=45°,E,F分别是过CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH,则GH的最小值为 .
15.如图,菱形ABCD的边长为26,对角线AC的长为48,延长AB至E,BF平分∠CBE,点G是BF上任意一点,则△ACG的面积为 .
三、解答题
16.如图,AD是△ABC的角平分线,AD的垂直平分线分别交AB、AC于点E、F,连接DE、DF.
(1)判断四边形AEDF的形状,并证明;
(2)当AB=9,AC=6时,求DF的长.
17.如图,在直角△AEC中,∠AEC=90°,B是边AE上一点,连接BC,O为AC的中点,过C作CD∥AB交BO延长线于D,且AC平分∠BCD,连接AD.
(1)求证:四边形ABCD是菱形.
(2)连接OE交BC于F,∠ACD=27°,求∠CFO的度数.
18.如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.
(1)求证:四边形AECD为菱形;
(2)若∠CEB=60°,DC=4,求△ABC的面积.
19.如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.
(1)求证:四边形AECD是菱形;
(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.
20.在Rt△ABC中,∠ACB=90°点D是边AB上的一个动点,连接CD.作AE∥DC,CE∥AB,连接ED.
(1)如图1,当CD⊥AB时,求证:AC=ED;
(2)如图2,当D是AB的中点时,
①四边形ADCE的形状是 ;请说明理由.
②若AB=5,ED=4,则四边形ADCE的面积为 .
21.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,点F在AD上,且AF=AB,连接BF交AE于点G,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若BF=10,AB=10,求菱形ABEF的面积.
22.如图,在 ABCD中,对角线AC和BD相交于点O,AD=10,AC=16,BD=12.
①求证: ABCD是菱形;
②延长BC至点E,连接OE交CD于点F,若∠E=∠ACD.求的值.
23.如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
答案
一、单选题
1.
【解答】解:∵菱形不具有的性质是对角线相等,
∴选项C符合题意,
故选:C.
2.
【解答】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
A、∵AC=BD,
∴平行四边形ABCD为矩形,故选项A不符合题意;
B、由AB=CD,不能判定四边形ABCD为菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、∵AC⊥BD,
∴平行四边形ABCD为菱形,故选项D符合题意;
故选:D.
3.
【解答】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,
∴∠AFB=90°,
∵E为AB的中点,且EF=2,
∴AB=2EF=4,
即菱形ABCD的边长是4,
故选:B.
4.
【解答】解:∵四边形ABCD是菱形,
∴AC垂直平分BD,
∴BC==,菱形的面积为=6,
设点A到BC的距离为h,
∴×h=6,
解得h=,
∴点A到BC的距离为.
故选:C.
5.
【解答】解:∵四边形ABCD为菱形,AC=6,BD=2,
∴AB=BC=CD=DA,AC⊥BD,OB=OD=BD=1,OA=OC=AC=3,
在Rt△OAB中,由勾股定理得:AB===,
∴菱形ABCD的周长=4AB=4,
故选:D.
6.
【解答】解:连接AC,EF,
∵四边形ABCD是菱形,
∴AB=BC,AB∥CD.
∴∠B+∠BCD=180°.
∵∠B=60°,
∴△ABC是等边三角形,∠BCD=120°.
∴∠BAC=∠ACB=60°,AB=AC.
∴∠ACF=∠B=60°.∠CAD=60°,
∵∠EAF=60°,
∴∠BAC﹣∠CAE=∠EAF﹣∠CAE.
∴∠BAE=∠CAF=α.
∴△ABE≌△ACF(ASA).∠FAD=60°﹣α,
∴∠B=∠ACF=60°,AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∴∠AFE=60°,
∴△AEF是等边三角形,
∴∠AFE=60°,
∵∠AFC=∠FAD+∠D,
∴∠EFC=∠FAD=60°﹣α,
∴∠CEF=α,
不能证出∠AFD=90°﹣α,
故选:D.
7.
【解答】解:在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=120°,BD=4,
∴∠BAD=60°,AD=AB,
则△ABD是等边三角形,
∴AB=AD=CD=BC=4,∠DAC=BAD=30°,
故AO=4cos30°=2,
∴AC=2AO=4.
故选:A.
8.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADO=∠CBO,
∵点O是BD的中点,
∴OD=OB,
在△DAO和△BCO中,
,
∴△DAO≌△BCO(ASA),
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形,
①∵四边形ABCD是平行四边形,AB=AD,
∴平行四边形ABCD是菱形;
③∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形;
④∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAC=∠DCA,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴AD=CD,
∴平行四边形ABCD是菱形.
综上所述:选择①③④,使得四边形ABCD是菱形,
故选:C.
9.
【解答】解:甲:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
由作图可知,AM=AB,BN=AB,
∴AM=BN,
∴四边形ABNM是平行四边形,
∵AM=AB,
∴平行四边形ABNM为菱形,故甲的作法正确;
乙:如图,设AH交BE于点O,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠BHO,
∵AH垂直平分BE,
∴BO=EO,
又∵∠AOE=∠HOB,
∴△AOE≌△HOB(ASA),
∴AE=HB,
∴四边形ABHE为平行四边形,
又∵AE=AB,
∴平行四边形ABHE为菱形,故乙的作法正确;
故选:C.
10.
【解答】解:过P作PM⊥CD于M,
∵四边形ABCD是菱形,
∴CD∥AB,AC⊥BD,OA=AC,OB=BD,AC平分∠BCD,
∵PF⊥BC于F,
∴PF=PM,
∵PE⊥AB于,PM⊥CD,CD∥AB,
∴P、E、M共线,
∴PE+PF=PE+PM=ME,
∵AC=8,BD=6,
∴OA=×8=4,OB=×6=3,
∴AB==5,
∵菱形ABCD的面积=AB EM=AC BD,
∴5EM=×6×8,
∴EM=.
∴PE+PF的值为.
故选:C.
二、填空题
11.
【解答】解:当添加“AD∥BC”时,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
当添加:“AB=CD”时,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
当添加“OB=OD”时,
∵AD=BC,AC⊥BD,
∴Rt△ADO≌Rt△CBO(HL),
∴AO=CO,DO=BO,
∴四边形ABCD是菱形;
当添加:“∠ADB=∠CBD”时,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
故答案为:AD∥BC(或AB=CD或OB=OD 或ADB=∠CBD等 ).
12.
【解答】解:∵四边形ABCD是菱形,
∴菱形ABCD的边长==,
∴菱形ABCD的周长是4,
故答案为:4.
13.
【解答】解:∵菱形是中心对称图形,
∴由图得:阴影的面积等于菱形面积的一半,
∵菱形的两条对角线的长分别为10和24,
∴菱形的面积为×10×24=120,
∴阴影部分的面积为60,
故答案为:60.
14.
【解答】解:连接AF,如图所示:
∵四边形ABCD是菱形,
∴AB=BC=8,
∵G,H分别为AE,EF的中点,
∴GH是△AEF的中位线,
∴,
当AF⊥BC时,AF最小,GH得到最小值,
则∠AFB=90°,
∵∠B=45°,
∴△ABF是等腰直角三角形,
∴,
∴,
即GH的最小值为,
故答案为:.
15.
【解答】解:如图,连接BD交AC于点O,
∵四边形ABCD是菱形,
∴BD与AC互相垂直平分,
∴OA=OC=24,
∴OB=OD==10,
∵DA∥CB,
∴∠DAB=∠CBE,
∵AC平分∠DAB,
∴∠CAB=DAB,
∵BF平分∠CBE,
∴∠FBE=CBE,
∴∠CAB=∠FBE,
∴AC∥FB,
∴S△CBG=S△ABG,
∴S△ACG=S△ABC=×AC OB=×48×10=240,
则△ACG的面积为240.
故答案为:240.
三、解答题
16.解:(1)四边形AEDF是菱形,理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD,
又∵EF⊥AD,
∴∠AOE=∠AOF=90°
在△AEO和△AFO中,
,
∴△AEO≌△AFO(ASA),
∴EO=FO,
∵EF垂直平分AD,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形,
又EF⊥AD,
∴平行四边形AEDF为菱形;
(2)由(1)知四边形AEDF为菱形,
∴DF∥AB,DF=AF,
∴=,
∴=,
∵AB=9,AC=6,
即=,
解得:DF=.
17.(1)证明:∵CD∥AB,
∴∠OAB=∠OCD,
∵O为AC的中点,
∴OA=OC,
在△AOB和△OCD中,
,
∴△AOB≌△OCD(ASA),
∴OB=OD,
又∵OA=OC,
∴四边形ABCD是平行四边形,
∵CD∥AB,
∴∠BAC=∠DCA,
∵AC平分∠BCD,
∴∠BCA=∠DCA,
∴∠BAC=∠BCA,
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)解:∵CD∥AB,∠AEC=90°,
∴∠DCE+∠AEC=180°,
∴∠DCE=90°,
∴∠OCE=90°﹣∠ACD=90°﹣27°=63°,
由(1)可知,四边形ABCD是菱形,
∴∠ACB=∠ACD=27°,∠BCD=2∠ACD=54°,
∴∠ECF=90°﹣∠BCD=90°﹣54°=36°,
∵∠AEC=90°,OA=OC,
∴OE=AC=OC,
∴∠OEC=∠OCE=63°,
∴∠CFO=∠OEC+∠ECF=63°+36°=99°,
即∠CFO的度数为99°.
18.(1)证明:∵E为AB中点,
∴AB=2AE,
∵AB=2CD,
∴2AE=2CD,
∴AE=CD,
∵AB∥CD,
∴四边形AECD是平行四边形,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵∠DCA=∠BAC,
∴∠DAC=∠DCA,
∴DA=DC,
∴四边形AECD为菱形.
(2)解:∵AE=CE=DC=4,
∴AE=BE=CE=4,
∵∠CEB=60°,
∴△BCE是等边三角形,
∴∠BCE=60°,BC=BE=4,
∵∠ACE=∠CAE,
∴∠CEB=∠ACE+∠CAE=2∠ACE=60°,
∴∠ACE=30°,
∴∠ACB=∠ACE+∠BCE=30°+60°=90°,
∵AB=2AE=8,
∴AC===4,
∴S△ABC=BC AC=×4×4=8,
∴△ABC的面积为8.
19.(1)证明:∵AD=CD,BD⊥AC,
∴OA=OC,
∵OE=OD,
∴四边形AECD是平行四边形,
∵AC⊥BD,
∴平行四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴OE⊥OA,
∵CF⊥AE,AB平分∠EAC,
∴BF=OB,
∴Rt△AFB≌Rt△AOB(HL),
∴AF=OA=OC,
∵BF=OB=3,BE=5,
∴EF=,
∴OE=OB+BE=3+5=8,
∵∠EFB=∠AOE=90°,∠∠FEB=∠∠AEO,
∴△AEO∽△EBF,
∴,
即,
∴AE=10,
∴AD=AE=10.
20.(1)证明:∵AE∥DC,CE∥AB,
∴四边形ADCE是平行四边形,
∵CD⊥AB,
∴∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=ED.
(2)①解:∵AE∥DC,CE∥AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴AD=CD=BD,
∴四边形ADCE是菱形,
故答案为菱形;
②∵四边形ADCE是菱形,
∴AC⊥DE,
又∵AC⊥BC,
∴DE∥BC,
∵CE∥AB,
∴四边形ECBD是平行四边形,
∴DE=BC=4,
∵AB=5,
∴AC==3,
∴四边形ADCE的面积为.
故答案为6.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∵AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴平行四边形ABEF是菱形;
(2)解:∵四边形ABEF为菱形,
∴AF=AB=10,AG⊥BF,
又∵BF=10,
∴BG=FG=5,
∴=,
∴,
∴菱形ABEF的面积.
22.(1)证明:∵四边形ABCD是平行四边形,AC=16,BD=12,
∴AO=CO=AC=8,BO=DO=BD=6,
∵AD=10,
∴AO2+DO2=AD2,
∴△AOD是直角三角形,且∠AOD=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:如图,过点O作OG∥CD,交BC于点G,
则==1,
∴BG=CG,
由(1)可知, ABCD是菱形,
∴BC=AD=CD=10,∠ACD=∠ACB,
∴BG=CG=BC=5,
∵∠E=∠ACD,∠ACB=∠E+∠COE,
∴∠ACB=∠ACD=2∠E=∠E+∠COE,
∴∠E=∠COE,
∴OC=CE=8,
∵OG∥CD,
∴==.
23.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
