人教版八年级数学下册 18.2.3正方形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册 18.2.3正方形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 553.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 00:00:00 | ||
图片预览



文档简介
18.2.3正方形
一、单选题
1.菱形、矩形、正方形都具有的性质是( )
A.对角线互相垂直
B.对角线相等
C.四条边相等,四个角相等
D.两组对边分别平行且相等
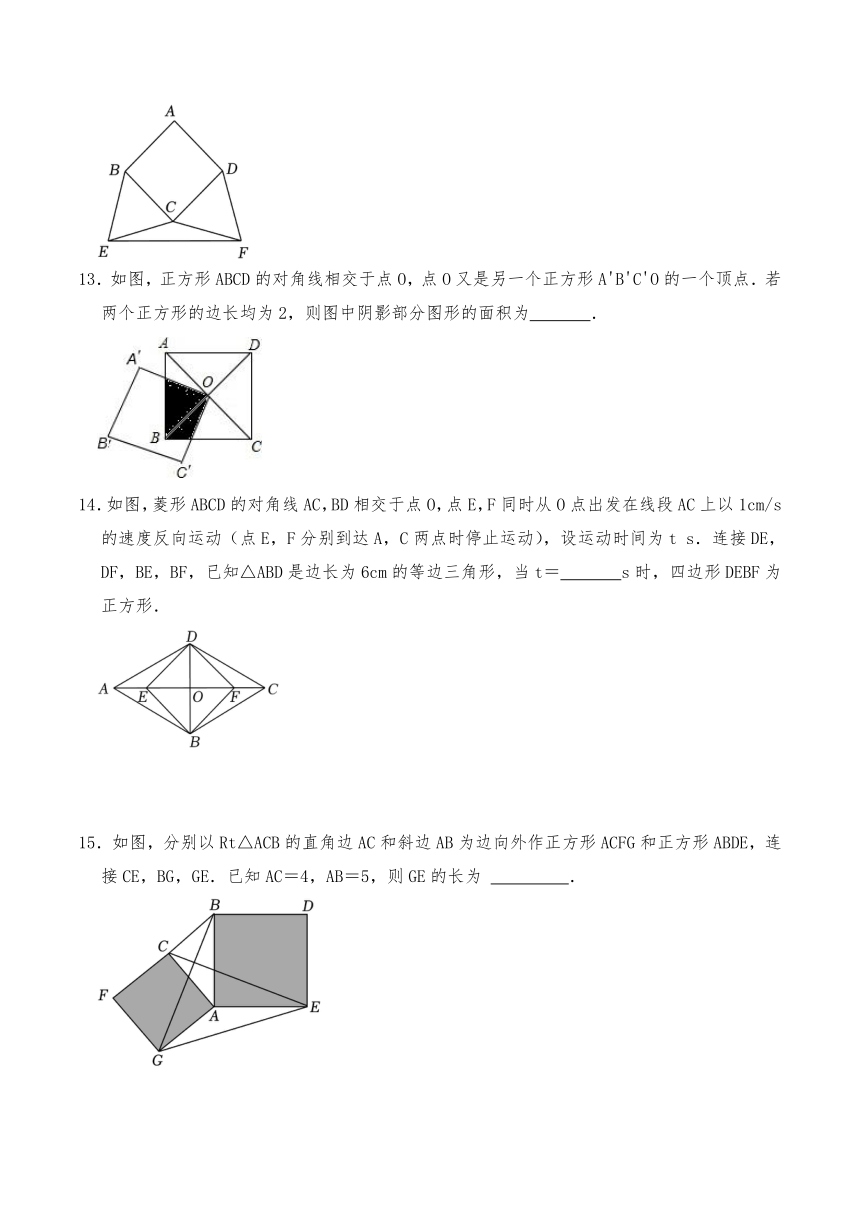
2.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当∠ABC=90°,平行四边形ABCD是矩形
B.当AC=BD,平行四边形ABCD是矩形
C.当AB=BC,平行四边形ABCD是菱形
D.当AC⊥BD,平行四边形ABCD是正方形
3.如图,已知四边形ABCD是平行四边形,下列三个结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是矩形;③当∠ABC=90°时,它是正方形.其中结论正确的有( )
A.0个 B.1个 C.2个 D.3个
4.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6cm,BC=8cm,则四边形EFGH的面积是( )
A.48cm2 B.32cm2 C.24cm2 D.12cm2
5.随着科技的进步,机器人在各个领域的应用越来越广泛.如图为正方形形状的擦窗机器人,其边长是28cm.在某次擦窗工作中,PM、PN为窗户的边缘,擦窗机器人的两个顶点A、B分别落在PM、PN上,PA=14cm,将擦窗机器人绕中心O逆时针旋转一定的角度,使得AD∥PM,则旋转角度是( )
A.15° B.30° C.45° D.60°
6.如图,正方形ABCD的边长为10,且AE=FC=8,BF=DE=6,则EF的长为( )
A.2 B. C. D.
7.小明用四根相同长度的木条制作了一个正方形学具(如图1),测得对角线,将正方形学具变形为菱形(如图2),∠DAB=60°,则图2中对角线AC的长为( )
A.20cm B. C. D.
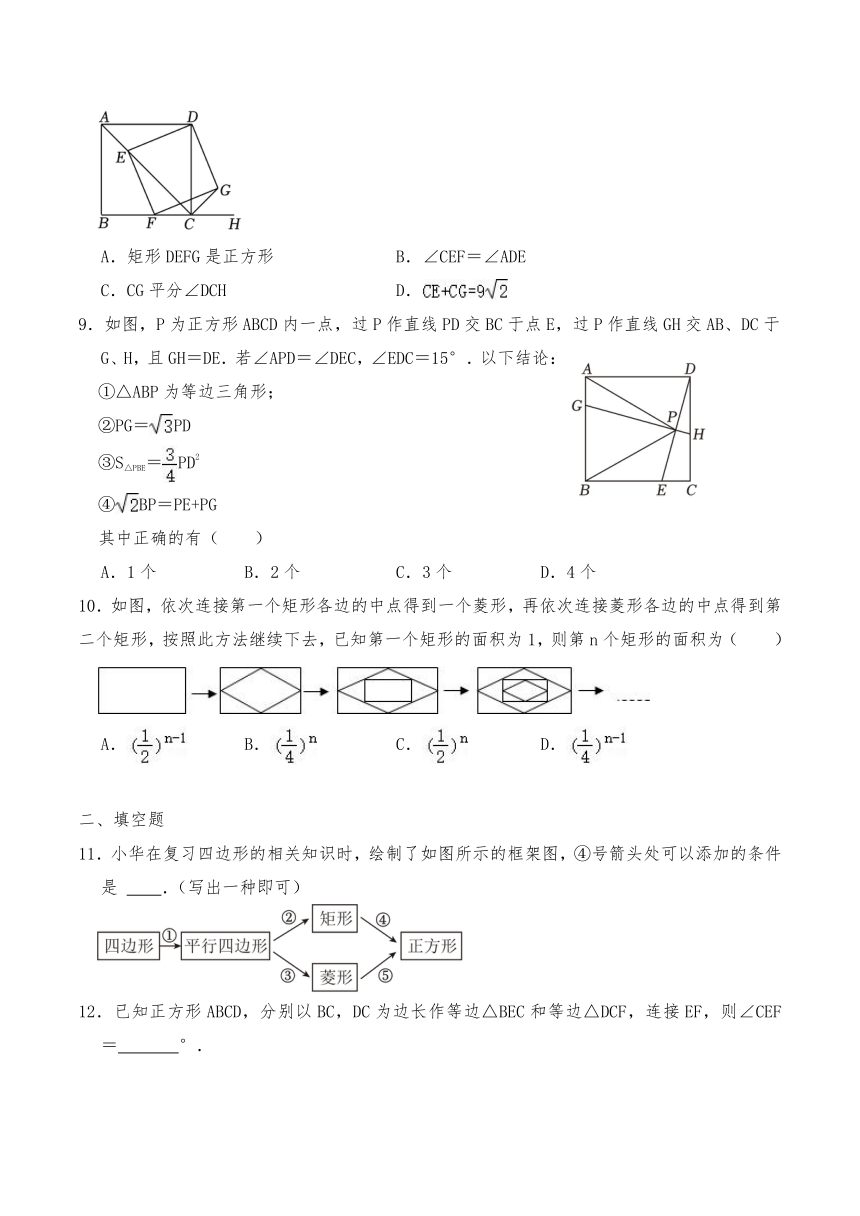
8.如图,正方形ABCD的边长为9,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG,下列结论中不正确的是( )
A.矩形DEFG是正方形 B.∠CEF=∠ADE
C.CG平分∠DCH D.
9.如图,P为正方形ABCD内一点,过P作直线PD交BC于点E,过P作直线GH交AB、DC于G、H,且GH=DE.若∠APD=∠DEC,∠EDC=15°.以下结论:
①△ABP为等边三角形;
②PG=PD
③S△PBE=PD2
④BP=PE+PG
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去,已知第一个矩形的面积为1,则第n个矩形的面积为( )
A. B. C. D.
二、填空题
11.小华在复习四边形的相关知识时,绘制了如图所示的框架图,④号箭头处可以添加的条件是 .(写出一种即可)
12.已知正方形ABCD,分别以BC,DC为边长作等边△BEC和等边△DCF,连接EF,则∠CEF= °.
13.如图,正方形ABCD的对角线相交于点O,点O又是另一个正方形A'B'C'O的一个顶点.若两个正方形的边长均为2,则图中阴影部分图形的面积为 .
14.如图,菱形ABCD的对角线AC,BD相交于点O,点E,F同时从O点出发在线段AC上以1cm/s的速度反向运动(点E,F分别到达A,C两点时停止运动),设运动时间为t s.连接DE,DF,BE,BF,已知△ABD是边长为6cm的等边三角形,当t= s时,四边形DEBF为正方形.
15.如图,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE.已知AC=4,AB=5,则GE的长为 .
三、解答题
16.如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
17.定义:若一个四边形满足三个条件①有一组对角互补,②一组邻边相等,③相等邻边的夹角为直角,则称这样的四边形为“直角等邻对补”四边形,简称为“直等补”四边形.根据以上定义,解答下列问题.
(1)如图1,四边形ABCD是正方形,点E在CD边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,请根据定义判断四边形AFCE是否是“直等补”四边形,并说明理由.
(2)如图2,已知四边形ABCD是“直等补”四边形,AB=AD,若AB=20,CD=4,求BC的长.
18.已知四边形ABCD和AEFG均为正方形.
(1)如图①,当点A,B,G三点在一条直线上时,连接BE,DG,请判断线段BE与DG的数量关系和位置关系,并说明理由;
(2)如图②,当点A,B,G三点不在一条直线上时,则(1)的结论是否成立?请说明理由.
19.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= 45 °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
20.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
21.如图,四边形AECF是菱形,对角线AC、EF交于点O,点D、B是对角线EF所在直线上两点,且DE=BF,连接AD、AB、CD、CB,∠ADO=45°.
(1)求证:四边形ABCD是正方形;
(2)若正方形ABCD的面积为72,BF=4,求点F到线段AE的距离.
22.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
23.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OF的长.
答案
一、单选题
1.
【解答】解:A、矩形的对角线不一定互相垂直,故本选项不符合题意;
B、菱形的对角线不一定相等,故本选项不符合题意;
C、矩形的四条边不一定相等,菱形的四个角不应当相等,故本选项不符合题意;
D、菱形、矩形、正方形的两组对边分别平行且相等,故本选项符合题意;
故选:D.
2.
【解答】解:∵四边形ABCD是平行四边形,
∴当∠ABC=90°,平行四边形ABCD是矩形,故选项A正确,不符合题意;
当AC=BD,平行四边形ABCD是矩形,故选项B正确,不符合题意;
当AB=BC,平行四边形ABCD是菱形,故选项C正确,不符合题意;
当AC⊥BD,平行四边形ABCD是菱形,但不一定是正方形,故选项D错误,符合题意;
故选:D.
3.
【解答】解:∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
故A正确;
∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
∴四边形ABCD不一定是矩形,
故B错误;
∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴四边形ABCD不一定是正方形,
故C错误,
故选:B.
4.
【解答】解:∵E,F,G,H分别是矩形ABCD各边的中点,AB=6cm,BC=8cm,
∴AE=AB=3cm,AH=AD=4cm,AE=DG,
∴S△EAH=×3×4=6(cm2),
在△EAH和△GDH中,
,
∴△EAH≌△GDH(SAS),
同理可得:△EAH≌△GDH≌△GCF≌△EBH,
∴四边形EFGH的面积为:6×8﹣6×4=24(cm2),
故选:C.
5.
【解答】解:如图,连接A'O,连接AO交A'D'于点E,
∵PA=14cm,AB=28cm,
∴cos∠PAB==,
∴∠PAB=60°,
∴∠PAO=105°,
∵A'D'∥PM,
∴∠PAO=∠A'EO=105°,
∴∠A'OA=180﹣105°﹣45°=30°,
∴旋转角为30°,
故选:B.
6.
【解答】解:延长BF交AE于点G,如图所示:
∵AE=FC,BF=DE,AD=CB,
∴△ADE≌△CBF(SSS),
∴∠DAE=∠BCF,∠ADE=∠CBF,∠DEA=∠BFC,
∵AD=10,DE=6,AE=8,102=62+82,
∴∠DEA=90°=∠BFC,
∵∠DAE+∠BAG=∠DAE+∠ADE=90°,∠CBF+∠ABG=∠CBF+∠BCF=90°,
∴∠BAG=∠ADE,∠ABG=∠BCF,
∴∠ADE=∠CBF=∠BAG,∠DAE=∠BCF=∠ABG,
∵AD=CB=BA,
∴△ADE≌△CBF≌△BAG(SAS),
∴∠AGB=90°,AG=DE=BF=6,BG=AE=FC=8,
∴∠EGF=90°,EG=AE﹣AG=2,GF=BG﹣BF=2,
∴.
故选:C.
7.
【解答】解:如图1,∵四边形ABCD是正方形,AC=10cm,
∴AB=AD=AC=10cm,
在图2中,连接BD交AC于O,
∵∠ABC=60°,AB=AD=10cm,
∴△ABD是等边三角形,则BD=10cm,
∵四边形ABCD是菱形,
∴BO==5cm,AO=CO,AC⊥BD,
∴AO===5(cm),
∴AC=2AO=10(cm),
故选:C.
8.
【解答】解:如图,作EK⊥BC于点K,EL⊥CD于点L,则∠EKF=∠ELD=90°,
∵四边形ABCD是正方形,
∴AB=CB,AD=CD,∠B=∠ADC=90°,
∴∠BCA=∠BAC=45°,∠DCA=∠DAC=45°,
∴∠BCA=∠DCA,
∴EK=EL,
∵∠EKC=∠ELC=∠KCL=90°,
∴四边形EKCL是矩形,
∵四边形DEFG是矩形,
∴∠KEL=∠FED=90,
∴∠FEK=∠DEL=90°﹣∠FEL,
∴△FEK≌△DEL(ASA),
∴DE=FE,
∴矩形DEFG是正方形,故A正确;
∵∠EDG=∠ADC=90°,
∴∠CDG=∠ADE=90°﹣∠CDE,
∵CD=AD,GD=ED,
∴△CDG≌△ADE(SAS),
∴CG=AE,
∴CE+CG=CE+AE=AC,
∵∠B=90°,AB=CB=9,
∴AC=AB=9,
∴CE+CG=9,故D正确;
∵△CDG≌△ADE(SAS),
∴∠DAE=∠DCG=45°,
∴CG平分∠DCH,故C正确;
∵∠ADE=∠DEL=∠FEK,≠∠CEF,
∴∠CEF≠∠ADE,故B不正确,
故选:B.
9.
【解答】解:①∵四边形ABCD是正方形,
∴AD=BC=AD,AD∥BC,∠BAD=∠ADC=∠DCE=90°,
∴∠ADE=∠DEC,
∵∠APD=∠DEC,
∴∠ADE=∠APD,
∴AP=AD,
∴AP=AB
∵∠EDC=15°,
∴∠ADP=90°﹣15°=75°=∠APD,
∴∠DAP=180°﹣75°﹣75°=30°,
∴∠BAP=90°﹣30°=60°,
∴△ABP是等边三角形;故①正确.
②如图,过点G作GK∥AD交CD于K,连接DG,
则∠GKH=∠ADC=90°=∠DKG,
∴∠GKH=∠DCE,
∵∠BAD=∠ADC=∠DKG=90°,
∴四边形ADKG是矩形,
∴GK=AD=CD,
∵GH=DE,
∴Rt△GHK≌Rt△DEC(HL),
∴∠GHK=∠DEC,
∵∠DEC+∠EDC=90°,
∴∠GHK+∠EDC=90°,
∴∠DPH=90°,
∴∠DPG=180°﹣∠DPH=90°,
∵∠DPG+∠BAD=180°,
∴四边形ADPG是圆内接四边形,
∴∠DGP=∠DAP=30°,
∴DG=2PD,
在Rt△DGP中,PG===PD,
故②正确;
③如图,过点P作PL⊥AD于L,交BC于J,过点E作EM⊥BP于M,
则四边形BALJ是矩形,
∴AL=BJ,∠BJP=∠ALP=90°,
∵AP=BP,
∴Rt△APL≌Rt△BPJ(HL),
∴PL=PJ,
在△PEJ和△PDL中,
,
∴△PEJ≌△PDL(ASA),
∴PJ=PD,
∵EM⊥BP,
∴∠BME=∠PME=90°,
∵LJ∥AB∥CD,
∴∠BPJ=∠ABP=60°,∠EPJ=∠EDC=15°,
∴∠EPM=∠BPJ﹣∠EPJ=45°,
∴△PEM是等腰直角三角形,
∴PM=EM=PE=PD,
∵∠ABP=60°,
∴∠EBM=30°,
∴BE=2ME=PD,
∴BM===PD,
∴BP=BM+PM=PD+PD=PD,
∴S△PBE=BP EM=×PD PD=PD2,
故③错误;
④过点B作BN⊥BP,交PG的延长线于N,连接DG,
∵∠GBN+∠GBP=90°,∠GBP+∠EBP=90°,
∴∠GBN=∠EBP,
∵∠EBG+∠BGP+∠EPG+∠BEP=360°,
∴∠BGP+∠BEP=360°﹣(∠EBG+∠EPG)=180°,
∵∠BGP+∠BGN=180°,
∴∠BGN=∠BEP,
由②知,∠DGP=30°,
∴∠GDP=60°,
∴∠ADG=90°﹣60°﹣15°=15°=∠EDC,
∴△DGA≌△DEC(ASA),
∴AG=CE,
∴BG=BE,
∴△BGN≌△BEP(ASA),
∴BN=BP,GN=PE,
∴△BPN是等腰直角三角形,
∴PN=BP,
∵PN=PG+GN=PE+PG,
∴BP=PE+PG,故④正确;
故选:C.
10.
【解答】解:已知第一个矩形的面积为1;
第二个矩形的面积为原来的()2×2﹣2=;
第三个矩形的面积是()2×3﹣2=;
…
故第n个矩形的面积为:()2n﹣2=()n﹣1.
故选:D.
二、填空题
11.
【解答】解:有一组邻边相等的矩形是正方形,
故答案为:有一组邻边相等(答案不唯一).
12.
【解答】解:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∵△BEC和△DCF都是等边三角形,
∴BC=EC,CD=CF,∠BCE=∠DCF=60°,
∴EC=FC,∠ECF=360°﹣∠BCD﹣∠BCE﹣∠DCF=150°,
∴∠CEF=15°,
故答案为:15.
13.
【解答】解:设A′O与AB交于点E,C′O与BC交于点F,
因为四边形ABCD是正方形,
所以AO=BO,∠AOB=90°,∠EAO=∠FBO.
∴∠AOE+∠BOE=90°.
又∠BOF+∠BOE=90°,
∴∠AOE=∠BOF.
所以△AEO≌△BFO(ASA).
∴四边形EBFO面积=△BEO面积+△BFO面积=△BEO面积+△AEO面积=△ABO面积.
因为正方形ABCD边长为2,
∴正方形面积为4,
∴△ABO面积为1.
所以阴影部分面积为1.
故答案为1.
14.
【解答】解:由题意得OE=OF=t cm,
∴EF=2t cm,
∵菱形ABCD的对角线AC,BD相交于点O,
∴OB=OD,AC⊥BD,
∴四边形DEBF是菱形,
∴当EF=BD时,四边形DEBF是正方形,
∵△ABD是边长为6cm的等边三角形,
∴BD=6cm,
∴由EF=BD得2t=6,
解得t=3,
∴当t=3s时,四边形DEBF是正方形,
故答案为:3.
15.
【解答】解:如图,作EP垂直于GA,交GA的延长线于点P.
∵∠CAB+∠PAB=90°,
∠PAB+∠PAE=90°,
∴∠CAB=∠PAE.
在△BCA和△EPA中,
∠BCA=∠EPA,
∠CAB=∠PAE,
BA=EA,
∴△BCA≌△EPA(AAS),
即PE=BC==3,
AP=AC=4.
∴GE==.
故答案为:.
三、解答题
16.(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°,
在△ADP和△CDP中
,
∴△ADP≌△CDP(SAS),
∴PA=PC,
∵∠PAE=∠E,
∴PA=PE,
∴PC=PE;
(2)∵在正方形ABCD中,∠ADC=90°,
∴∠EDF=90°,
由(1)知,△ADP≌△CDP,
∴∠DAP=∠DCP,
∵∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°.
17.解:(1)四边形AFCE是“直等补”四边形,
理由:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=∠ABC=90°,
∴∠ABF=90°,
在△ABF与△ADE中,
,
∴△ABF≌△ADE(SAS),
∴AF=AE,∠BAF=∠DAE,
∴∠BAF+∠BAE=∠DAE+∠BAE=90°,
∴∠FAE=90°,
∴∠FAE+∠C=180°,
∴四边形AFCE是“直等补”四边形;
(2)连接BD,
∵四边形ABCD是“直等补”四边形,AB=AD,
∴∠BAD=90°,
∴∠C+∠BAD=180°,
∴∠C=90°,
∵AB=AD=20,
∴BD==20,
∵CD=4,
∴BC==28.
18.解:(1)BE=DG,BE⊥DG.理由:
延长BE交DG于点N.如图:
∵四边形ABCD和AEFG均为正方形,
∴AB=AD,∠BAD=∠EAG=90°,AE=AG.
∴△ABE≌△ADG(SAS).
∴BE=DG,∠ABE=∠ADG.
∵∠ABE+∠AEB=90°,∠AEB=∠DEN,
∴∠ADG+∠DEN=90°.
即∠DNE=90°.
∴BE⊥DG.
(2)解:当点A,B,G三点不在一条直线上时,(1)的结论仍然成立.理由:
∵四边形ABCD和AEFG均为正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°.
∴∠BAD+∠DAE=∠EAG+∠DAE,
∴∠BAE=∠DAG.
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS).
∴BE=DG,∠ABE=∠ADG.
∵∠ABE+∠AOB=90°,∠AOB=∠DON,
∴∠ADG+∠AOB=∠ADG+∠DON=90°.
即∠DNO=90°.
∴BE⊥DG.
∴(1)的结论仍然成立.
19.(1)解:∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFE=DFE,∠AEF=BEF,
∴∠AEF+∠AFE=(∠DFE+∠BEF)=270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①证明:作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②解:设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=6,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2.
20.(1)证明:作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中.AC=AB=2,
∵EC=,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=.
(3)①当DE与AD的夹角为30°时,点F在BC边上,∠ADE=30°,
则∠CDE=90°﹣30°=60°,
在四边形CDEF中,由四边形内角和定理得:∠EFC=360°﹣90°﹣90°﹣60°=120°,
②当DE与DC的夹角为30°时,点F在BC的延长线上,∠CDE=30°,如图3所示:
∵∠HCF=∠DEF=90°,∠CHF=∠EHD,
∴∠EFC=∠CDE=30°,
综上所述,∠EFC=120°或30°.
21.(1)证明:∵菱形AECF的对角线AC和EF交于点O,
∴AC⊥EF,OA=OC,OE=OF,
∵BE=DF,
∴BO=DO,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∵∠ADO=45°,
∴∠DAO=∠ADO=45°,
∴AO=DO,
∴AC=BD,
∴四边形ABCD是正方形;
(2)解:∵正方形ABCD的面积为72,
∴AC BD=72,
∴×4BO2=72,
∴BO=DO=CO=AO=6,
∴AC=12,
∵BF=4,
∴OF=2,
∵四边形ABCD是菱形,
∴EF=2EO=2OF=4,AC⊥EF,
∴菱形AFCE的面积=AC EF=24,
在Rt△AOE中,AE==2,
设点F到线段AE的距离为h,
∴AE h=24,
即2h=24,
∴h=.
即点F到线段AE的距离为.
22.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
23.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)证明:∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,
,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)解:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD=,∠DAG=∠ADG=45°,
∴DF=﹣1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=OF=﹣1.
∴OF=﹣1.
一、单选题
1.菱形、矩形、正方形都具有的性质是( )
A.对角线互相垂直
B.对角线相等
C.四条边相等,四个角相等
D.两组对边分别平行且相等
2.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当∠ABC=90°,平行四边形ABCD是矩形
B.当AC=BD,平行四边形ABCD是矩形
C.当AB=BC,平行四边形ABCD是菱形
D.当AC⊥BD,平行四边形ABCD是正方形
3.如图,已知四边形ABCD是平行四边形,下列三个结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是矩形;③当∠ABC=90°时,它是正方形.其中结论正确的有( )
A.0个 B.1个 C.2个 D.3个
4.如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6cm,BC=8cm,则四边形EFGH的面积是( )
A.48cm2 B.32cm2 C.24cm2 D.12cm2
5.随着科技的进步,机器人在各个领域的应用越来越广泛.如图为正方形形状的擦窗机器人,其边长是28cm.在某次擦窗工作中,PM、PN为窗户的边缘,擦窗机器人的两个顶点A、B分别落在PM、PN上,PA=14cm,将擦窗机器人绕中心O逆时针旋转一定的角度,使得AD∥PM,则旋转角度是( )
A.15° B.30° C.45° D.60°
6.如图,正方形ABCD的边长为10,且AE=FC=8,BF=DE=6,则EF的长为( )
A.2 B. C. D.
7.小明用四根相同长度的木条制作了一个正方形学具(如图1),测得对角线,将正方形学具变形为菱形(如图2),∠DAB=60°,则图2中对角线AC的长为( )
A.20cm B. C. D.
8.如图,正方形ABCD的边长为9,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG,下列结论中不正确的是( )
A.矩形DEFG是正方形 B.∠CEF=∠ADE
C.CG平分∠DCH D.
9.如图,P为正方形ABCD内一点,过P作直线PD交BC于点E,过P作直线GH交AB、DC于G、H,且GH=DE.若∠APD=∠DEC,∠EDC=15°.以下结论:
①△ABP为等边三角形;
②PG=PD
③S△PBE=PD2
④BP=PE+PG
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去,已知第一个矩形的面积为1,则第n个矩形的面积为( )
A. B. C. D.
二、填空题
11.小华在复习四边形的相关知识时,绘制了如图所示的框架图,④号箭头处可以添加的条件是 .(写出一种即可)
12.已知正方形ABCD,分别以BC,DC为边长作等边△BEC和等边△DCF,连接EF,则∠CEF= °.
13.如图,正方形ABCD的对角线相交于点O,点O又是另一个正方形A'B'C'O的一个顶点.若两个正方形的边长均为2,则图中阴影部分图形的面积为 .
14.如图,菱形ABCD的对角线AC,BD相交于点O,点E,F同时从O点出发在线段AC上以1cm/s的速度反向运动(点E,F分别到达A,C两点时停止运动),设运动时间为t s.连接DE,DF,BE,BF,已知△ABD是边长为6cm的等边三角形,当t= s时,四边形DEBF为正方形.
15.如图,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE.已知AC=4,AB=5,则GE的长为 .
三、解答题
16.如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
17.定义:若一个四边形满足三个条件①有一组对角互补,②一组邻边相等,③相等邻边的夹角为直角,则称这样的四边形为“直角等邻对补”四边形,简称为“直等补”四边形.根据以上定义,解答下列问题.
(1)如图1,四边形ABCD是正方形,点E在CD边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,请根据定义判断四边形AFCE是否是“直等补”四边形,并说明理由.
(2)如图2,已知四边形ABCD是“直等补”四边形,AB=AD,若AB=20,CD=4,求BC的长.
18.已知四边形ABCD和AEFG均为正方形.
(1)如图①,当点A,B,G三点在一条直线上时,连接BE,DG,请判断线段BE与DG的数量关系和位置关系,并说明理由;
(2)如图②,当点A,B,G三点不在一条直线上时,则(1)的结论是否成立?请说明理由.
19.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= 45 °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
20.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
21.如图,四边形AECF是菱形,对角线AC、EF交于点O,点D、B是对角线EF所在直线上两点,且DE=BF,连接AD、AB、CD、CB,∠ADO=45°.
(1)求证:四边形ABCD是正方形;
(2)若正方形ABCD的面积为72,BF=4,求点F到线段AE的距离.
22.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
23.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OF的长.
答案
一、单选题
1.
【解答】解:A、矩形的对角线不一定互相垂直,故本选项不符合题意;
B、菱形的对角线不一定相等,故本选项不符合题意;
C、矩形的四条边不一定相等,菱形的四个角不应当相等,故本选项不符合题意;
D、菱形、矩形、正方形的两组对边分别平行且相等,故本选项符合题意;
故选:D.
2.
【解答】解:∵四边形ABCD是平行四边形,
∴当∠ABC=90°,平行四边形ABCD是矩形,故选项A正确,不符合题意;
当AC=BD,平行四边形ABCD是矩形,故选项B正确,不符合题意;
当AB=BC,平行四边形ABCD是菱形,故选项C正确,不符合题意;
当AC⊥BD,平行四边形ABCD是菱形,但不一定是正方形,故选项D错误,符合题意;
故选:D.
3.
【解答】解:∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
故A正确;
∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
∴四边形ABCD不一定是矩形,
故B错误;
∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴四边形ABCD不一定是正方形,
故C错误,
故选:B.
4.
【解答】解:∵E,F,G,H分别是矩形ABCD各边的中点,AB=6cm,BC=8cm,
∴AE=AB=3cm,AH=AD=4cm,AE=DG,
∴S△EAH=×3×4=6(cm2),
在△EAH和△GDH中,
,
∴△EAH≌△GDH(SAS),
同理可得:△EAH≌△GDH≌△GCF≌△EBH,
∴四边形EFGH的面积为:6×8﹣6×4=24(cm2),
故选:C.
5.
【解答】解:如图,连接A'O,连接AO交A'D'于点E,
∵PA=14cm,AB=28cm,
∴cos∠PAB==,
∴∠PAB=60°,
∴∠PAO=105°,
∵A'D'∥PM,
∴∠PAO=∠A'EO=105°,
∴∠A'OA=180﹣105°﹣45°=30°,
∴旋转角为30°,
故选:B.
6.
【解答】解:延长BF交AE于点G,如图所示:
∵AE=FC,BF=DE,AD=CB,
∴△ADE≌△CBF(SSS),
∴∠DAE=∠BCF,∠ADE=∠CBF,∠DEA=∠BFC,
∵AD=10,DE=6,AE=8,102=62+82,
∴∠DEA=90°=∠BFC,
∵∠DAE+∠BAG=∠DAE+∠ADE=90°,∠CBF+∠ABG=∠CBF+∠BCF=90°,
∴∠BAG=∠ADE,∠ABG=∠BCF,
∴∠ADE=∠CBF=∠BAG,∠DAE=∠BCF=∠ABG,
∵AD=CB=BA,
∴△ADE≌△CBF≌△BAG(SAS),
∴∠AGB=90°,AG=DE=BF=6,BG=AE=FC=8,
∴∠EGF=90°,EG=AE﹣AG=2,GF=BG﹣BF=2,
∴.
故选:C.
7.
【解答】解:如图1,∵四边形ABCD是正方形,AC=10cm,
∴AB=AD=AC=10cm,
在图2中,连接BD交AC于O,
∵∠ABC=60°,AB=AD=10cm,
∴△ABD是等边三角形,则BD=10cm,
∵四边形ABCD是菱形,
∴BO==5cm,AO=CO,AC⊥BD,
∴AO===5(cm),
∴AC=2AO=10(cm),
故选:C.
8.
【解答】解:如图,作EK⊥BC于点K,EL⊥CD于点L,则∠EKF=∠ELD=90°,
∵四边形ABCD是正方形,
∴AB=CB,AD=CD,∠B=∠ADC=90°,
∴∠BCA=∠BAC=45°,∠DCA=∠DAC=45°,
∴∠BCA=∠DCA,
∴EK=EL,
∵∠EKC=∠ELC=∠KCL=90°,
∴四边形EKCL是矩形,
∵四边形DEFG是矩形,
∴∠KEL=∠FED=90,
∴∠FEK=∠DEL=90°﹣∠FEL,
∴△FEK≌△DEL(ASA),
∴DE=FE,
∴矩形DEFG是正方形,故A正确;
∵∠EDG=∠ADC=90°,
∴∠CDG=∠ADE=90°﹣∠CDE,
∵CD=AD,GD=ED,
∴△CDG≌△ADE(SAS),
∴CG=AE,
∴CE+CG=CE+AE=AC,
∵∠B=90°,AB=CB=9,
∴AC=AB=9,
∴CE+CG=9,故D正确;
∵△CDG≌△ADE(SAS),
∴∠DAE=∠DCG=45°,
∴CG平分∠DCH,故C正确;
∵∠ADE=∠DEL=∠FEK,≠∠CEF,
∴∠CEF≠∠ADE,故B不正确,
故选:B.
9.
【解答】解:①∵四边形ABCD是正方形,
∴AD=BC=AD,AD∥BC,∠BAD=∠ADC=∠DCE=90°,
∴∠ADE=∠DEC,
∵∠APD=∠DEC,
∴∠ADE=∠APD,
∴AP=AD,
∴AP=AB
∵∠EDC=15°,
∴∠ADP=90°﹣15°=75°=∠APD,
∴∠DAP=180°﹣75°﹣75°=30°,
∴∠BAP=90°﹣30°=60°,
∴△ABP是等边三角形;故①正确.
②如图,过点G作GK∥AD交CD于K,连接DG,
则∠GKH=∠ADC=90°=∠DKG,
∴∠GKH=∠DCE,
∵∠BAD=∠ADC=∠DKG=90°,
∴四边形ADKG是矩形,
∴GK=AD=CD,
∵GH=DE,
∴Rt△GHK≌Rt△DEC(HL),
∴∠GHK=∠DEC,
∵∠DEC+∠EDC=90°,
∴∠GHK+∠EDC=90°,
∴∠DPH=90°,
∴∠DPG=180°﹣∠DPH=90°,
∵∠DPG+∠BAD=180°,
∴四边形ADPG是圆内接四边形,
∴∠DGP=∠DAP=30°,
∴DG=2PD,
在Rt△DGP中,PG===PD,
故②正确;
③如图,过点P作PL⊥AD于L,交BC于J,过点E作EM⊥BP于M,
则四边形BALJ是矩形,
∴AL=BJ,∠BJP=∠ALP=90°,
∵AP=BP,
∴Rt△APL≌Rt△BPJ(HL),
∴PL=PJ,
在△PEJ和△PDL中,
,
∴△PEJ≌△PDL(ASA),
∴PJ=PD,
∵EM⊥BP,
∴∠BME=∠PME=90°,
∵LJ∥AB∥CD,
∴∠BPJ=∠ABP=60°,∠EPJ=∠EDC=15°,
∴∠EPM=∠BPJ﹣∠EPJ=45°,
∴△PEM是等腰直角三角形,
∴PM=EM=PE=PD,
∵∠ABP=60°,
∴∠EBM=30°,
∴BE=2ME=PD,
∴BM===PD,
∴BP=BM+PM=PD+PD=PD,
∴S△PBE=BP EM=×PD PD=PD2,
故③错误;
④过点B作BN⊥BP,交PG的延长线于N,连接DG,
∵∠GBN+∠GBP=90°,∠GBP+∠EBP=90°,
∴∠GBN=∠EBP,
∵∠EBG+∠BGP+∠EPG+∠BEP=360°,
∴∠BGP+∠BEP=360°﹣(∠EBG+∠EPG)=180°,
∵∠BGP+∠BGN=180°,
∴∠BGN=∠BEP,
由②知,∠DGP=30°,
∴∠GDP=60°,
∴∠ADG=90°﹣60°﹣15°=15°=∠EDC,
∴△DGA≌△DEC(ASA),
∴AG=CE,
∴BG=BE,
∴△BGN≌△BEP(ASA),
∴BN=BP,GN=PE,
∴△BPN是等腰直角三角形,
∴PN=BP,
∵PN=PG+GN=PE+PG,
∴BP=PE+PG,故④正确;
故选:C.
10.
【解答】解:已知第一个矩形的面积为1;
第二个矩形的面积为原来的()2×2﹣2=;
第三个矩形的面积是()2×3﹣2=;
…
故第n个矩形的面积为:()2n﹣2=()n﹣1.
故选:D.
二、填空题
11.
【解答】解:有一组邻边相等的矩形是正方形,
故答案为:有一组邻边相等(答案不唯一).
12.
【解答】解:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∵△BEC和△DCF都是等边三角形,
∴BC=EC,CD=CF,∠BCE=∠DCF=60°,
∴EC=FC,∠ECF=360°﹣∠BCD﹣∠BCE﹣∠DCF=150°,
∴∠CEF=15°,
故答案为:15.
13.
【解答】解:设A′O与AB交于点E,C′O与BC交于点F,
因为四边形ABCD是正方形,
所以AO=BO,∠AOB=90°,∠EAO=∠FBO.
∴∠AOE+∠BOE=90°.
又∠BOF+∠BOE=90°,
∴∠AOE=∠BOF.
所以△AEO≌△BFO(ASA).
∴四边形EBFO面积=△BEO面积+△BFO面积=△BEO面积+△AEO面积=△ABO面积.
因为正方形ABCD边长为2,
∴正方形面积为4,
∴△ABO面积为1.
所以阴影部分面积为1.
故答案为1.
14.
【解答】解:由题意得OE=OF=t cm,
∴EF=2t cm,
∵菱形ABCD的对角线AC,BD相交于点O,
∴OB=OD,AC⊥BD,
∴四边形DEBF是菱形,
∴当EF=BD时,四边形DEBF是正方形,
∵△ABD是边长为6cm的等边三角形,
∴BD=6cm,
∴由EF=BD得2t=6,
解得t=3,
∴当t=3s时,四边形DEBF是正方形,
故答案为:3.
15.
【解答】解:如图,作EP垂直于GA,交GA的延长线于点P.
∵∠CAB+∠PAB=90°,
∠PAB+∠PAE=90°,
∴∠CAB=∠PAE.
在△BCA和△EPA中,
∠BCA=∠EPA,
∠CAB=∠PAE,
BA=EA,
∴△BCA≌△EPA(AAS),
即PE=BC==3,
AP=AC=4.
∴GE==.
故答案为:.
三、解答题
16.(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°,
在△ADP和△CDP中
,
∴△ADP≌△CDP(SAS),
∴PA=PC,
∵∠PAE=∠E,
∴PA=PE,
∴PC=PE;
(2)∵在正方形ABCD中,∠ADC=90°,
∴∠EDF=90°,
由(1)知,△ADP≌△CDP,
∴∠DAP=∠DCP,
∵∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°.
17.解:(1)四边形AFCE是“直等补”四边形,
理由:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=∠ABC=90°,
∴∠ABF=90°,
在△ABF与△ADE中,
,
∴△ABF≌△ADE(SAS),
∴AF=AE,∠BAF=∠DAE,
∴∠BAF+∠BAE=∠DAE+∠BAE=90°,
∴∠FAE=90°,
∴∠FAE+∠C=180°,
∴四边形AFCE是“直等补”四边形;
(2)连接BD,
∵四边形ABCD是“直等补”四边形,AB=AD,
∴∠BAD=90°,
∴∠C+∠BAD=180°,
∴∠C=90°,
∵AB=AD=20,
∴BD==20,
∵CD=4,
∴BC==28.
18.解:(1)BE=DG,BE⊥DG.理由:
延长BE交DG于点N.如图:
∵四边形ABCD和AEFG均为正方形,
∴AB=AD,∠BAD=∠EAG=90°,AE=AG.
∴△ABE≌△ADG(SAS).
∴BE=DG,∠ABE=∠ADG.
∵∠ABE+∠AEB=90°,∠AEB=∠DEN,
∴∠ADG+∠DEN=90°.
即∠DNE=90°.
∴BE⊥DG.
(2)解:当点A,B,G三点不在一条直线上时,(1)的结论仍然成立.理由:
∵四边形ABCD和AEFG均为正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°.
∴∠BAD+∠DAE=∠EAG+∠DAE,
∴∠BAE=∠DAG.
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS).
∴BE=DG,∠ABE=∠ADG.
∵∠ABE+∠AOB=90°,∠AOB=∠DON,
∴∠ADG+∠AOB=∠ADG+∠DON=90°.
即∠DNO=90°.
∴BE⊥DG.
∴(1)的结论仍然成立.
19.(1)解:∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFE=DFE,∠AEF=BEF,
∴∠AEF+∠AFE=(∠DFE+∠BEF)=270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①证明:作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②解:设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=6,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2.
20.(1)证明:作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中.AC=AB=2,
∵EC=,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=.
(3)①当DE与AD的夹角为30°时,点F在BC边上,∠ADE=30°,
则∠CDE=90°﹣30°=60°,
在四边形CDEF中,由四边形内角和定理得:∠EFC=360°﹣90°﹣90°﹣60°=120°,
②当DE与DC的夹角为30°时,点F在BC的延长线上,∠CDE=30°,如图3所示:
∵∠HCF=∠DEF=90°,∠CHF=∠EHD,
∴∠EFC=∠CDE=30°,
综上所述,∠EFC=120°或30°.
21.(1)证明:∵菱形AECF的对角线AC和EF交于点O,
∴AC⊥EF,OA=OC,OE=OF,
∵BE=DF,
∴BO=DO,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∵∠ADO=45°,
∴∠DAO=∠ADO=45°,
∴AO=DO,
∴AC=BD,
∴四边形ABCD是正方形;
(2)解:∵正方形ABCD的面积为72,
∴AC BD=72,
∴×4BO2=72,
∴BO=DO=CO=AO=6,
∴AC=12,
∵BF=4,
∴OF=2,
∵四边形ABCD是菱形,
∴EF=2EO=2OF=4,AC⊥EF,
∴菱形AFCE的面积=AC EF=24,
在Rt△AOE中,AE==2,
设点F到线段AE的距离为h,
∴AE h=24,
即2h=24,
∴h=.
即点F到线段AE的距离为.
22.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
23.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)证明:∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,
,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)解:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD=,∠DAG=∠ADG=45°,
∴DF=﹣1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=OF=﹣1.
∴OF=﹣1.
