从实验区高考试题窥探高中新课程概率教学的方向
文档属性
| 名称 | 从实验区高考试题窥探高中新课程概率教学的方向 |

|
|
| 格式 | rar | ||
| 文件大小 | 98.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-10 00:00:00 | ||
图片预览

文档简介
从实验区高考试题窥探高中新课程概率教学的方向
山西省教育科学研究院 薛红霞
走进高中新课程,面对教材的变化,很多老师不适应,又因为受已有教学经验的影响,在教学中有意无意地走回到大纲教材中,而且经常以“高考怎么考”为借口来佐证这种教学行为是正确的。高考怎么考,教学该怎么教?本文欲通过剖析实验区高考试题,窥探新课程概率部分的教学该怎么教。
一、课标与大纲的区别
《高中数学课程标准(实验稿)》简称课标。与大纲相比较,课标中对概率内容的设置一分为二,分别安排在数学3和选修2-3中,并调整了排列组合、统计、概率的位置。这样做是釜底抽薪,给以往在概率教学中过分注重计数的计算降温,达到突出概率本质的目的。
在大纲教材中,先学排列组合,紧接着学习概率,而且概率的学习以古典概型为主,统计则安排在选修部分。这样设置给大家的印象是:概率简单,只要分清楚几种概率模型即可,关键是要把数算对。因此概率学习、训练的重心就放在了计数上。学生对概率的理解完全是确定性数学下的套模型、计数,而没有概率思想。
课标教材改变了上述安排,先学统计(抽样、数据收集、整理、分析等),紧接着学习概率的意义、古典概型、几何概型。对于文科的学生这就是高中阶段概率学习的全部,对于理科学生将在2-3中继续学习概率和统计案例。这样安排,在概率学习的第一阶段,弱化了概率学习中的计算(没有计数工具、古典概型中也只是学习等可能事件和互斥事件的概率),强化了对概率本质的理解,尤其是基于统计学习概率,并增加了“用模拟方法(包括计算器产生随机数来进行模拟)估计概率,初步体会几何概型的意义”,如果在教学中能真正落实课标的要求,让学生经历运用计算器、计算机来处理数据,进行模拟活动的全过程,就可以让学生更好地体会统计思想和概率的意义。这样的教学才是真正具有概率思想的教学。
二、实际教学现象
面对上述变化,有些教师很不适应,在实际教学中体现为一强一弱。
强:即补充排列组合,补充的目的是为了计数方便,造成的结果是加重了学生的负担,尤其是对将来侧重文科的学生这种做法更是浪费时间,因为课标中不要求侧文的学生学习计数原理。
弱:即弱化数学3中概率的意义,忽略教材(人教A版)中整数值随机数的产生和均匀随机数的产生两节内容的学习。有的教师一带而过,有的教师采取让学生自己看书的方法敷衍了事。
这一强一弱反应出教师对课标的不理解,教学的重心放在了计数上,导致学生没有概率统计的思想,只是一个计算的奴隶。比如在我省的模块测试题中设计了如下一道试题:
甲乙两人玩一种游戏,为了研究这种游戏设计如下流程图:
(1)请你简述这种游戏的规则;
(2)假设n=1000时,k=400,求p的值.
(3)通过试验得到下列数据,根据这些数据估计甲胜的概率(精确到0.01);
次数
3000
5000
10000
20000
50000
100000
p
0.418
0.409
0.4136
0.4145
0.4185
0.41608
(4)这种游戏对甲是否公平,为什么?
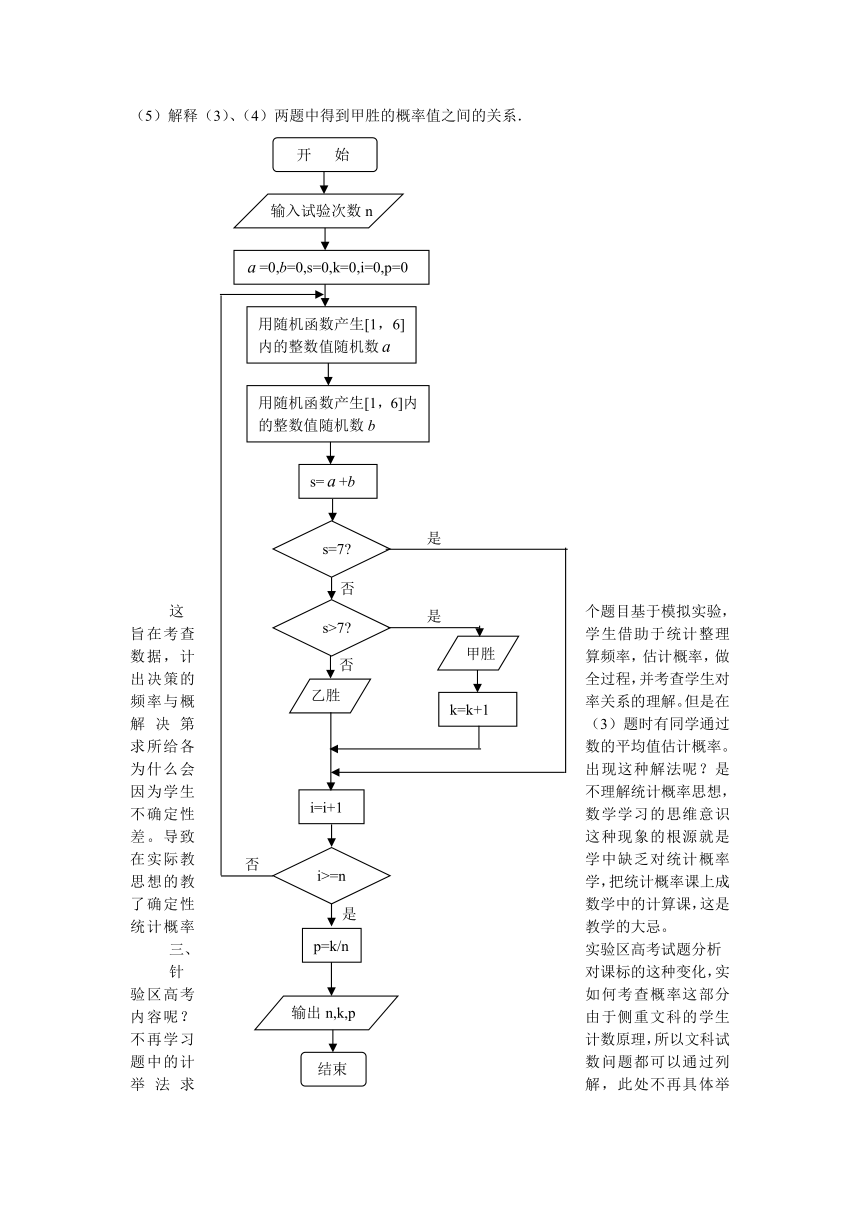
(5)解释(3)、(4)两题中得到甲胜的概率值之间的关系.
这个题目基于模拟实验,旨在考查学生借助于统计整理数据,计算频率,估计概率,做出决策的全过程,并考查学生对频率与概率关系的理解。但是在解决第(3)题时有同学通过求所给各数的平均值估计概率。为什么会出现这种解法呢?是因为学生不理解统计概率思想,不确定性数学学习的思维意识差。导致这种现象的根源就是在实际教学中缺乏对统计概率思想的教学,把统计概率课上成了确定性数学中的计算课,这是统计概率教学的大忌。
三、 实验区高考试题分析
针对课标的这种变化,实验区高考如何考查概率这部分内容呢?由于侧重文科的学生不再学习计数原理,所以文科试题中的计数问题都可以通过列举法求解,此处不再具体举例。对于理科的试题,由于学生在2-3中还要学习计数原理,所以在试题中依然会出现将排列组合与概率结合考查的试题,但是这样的试题所占比重减少,而且除个别试题外,这些题目中的计数问题都比较简单。本文以2009年实验区理科9套数学试卷中的6道概率题为例进行分析。这6道题目中体现的新课程试卷的特点如下。
1. 统计概率结合,考查学生对数据的处理和运用数据决策的能力。
例1 (2009年广东理17)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间进行分组,得到频率分布直方图(如图1).
(1)求直方图中的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
(结果用分数表示.已知).
这个题目完整的考查了学生通过统计处理数据、进行决策的全过程,是具有实际使用价值的,对于学生未来的生活工作是有意义的。其中第(3)问考查互斥事件、独立重复试验的概率计算,但是在解决该问时是如下求得所需要的概率值的:该城市一年中每天空气质量为良或轻微污染的概率为,则空气质量不为良且不为轻微污染的概率为。可见这是运用频率值估计概率值,考查了概率的意义,而不是通过计数计算得出的。这种考查方式反映了课标的要求。
2. 考查模拟实验,促进学生更好的体会统计思想和概率意义。
例2 (2009福建理8)已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35 B. 0.25 C. 0.20 D. 0.15
这个题目是以模拟实验为背景命制的。题干中已经设计了模拟实验,并产生了20组模拟实验的结果。根据题意,所求的是事件“该运动员三次投篮中恰有两次命中”的概率,根据模拟实验中数字代表的含义,这个事件对应的实验结果是“三个数字中恰有两个数字是1,2,3,4中的两个”。统计所给数据可知,这20组数据中有5组符合要求,因此可以估计所求概率值为。在教学中如果认真落实了课标的要求,那么这个题目的解决就是轻车熟路,简单易行。
3. 考查新增内容,注重完整的概率过程。
例3 (2009山东理11)在区间[-1,1]上随机取一个数x,的值介于0到之间的概率为( ).
A. B. C. D. w.w.w.k.s.5.u.c.o.m
例4 (2009年辽宁理19)某人向一目标射击4次,每次击中目标的概率为。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(1)设X表示目标被击中的次数,求X的分布列;
(2)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A)。
这两个题目考查的是几何概型,例3考查的是线性测度的几何概型,例4考查的是面积测度的几何概型。关键在于这两个题目考查的是完整的几何概型问题,不是从其中截取了某一部分。实际教学中有部分教师却是把教学的重点放在了几何概型中的变换部分,认为这部分好出题,其本质还是属于确定性数学问题。通过分析这两个题目,应该认识清楚以后的教学方向。
4. 公式计数与列举法计数在计算概率时各显其优势。
例5 (2009年江苏5)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为 。
例6 (2009年安徽理10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )
A. B. C. D.
这两个题目都是考查等可能事件的概率,而且它们的共同特点是:在计算样本空间的总数时都可以借助于组合计数,但是在计算事件A所包含的基本事件的个数时都只能用列举法计数。这种考查思路可以看出,并不是一定要用排列组合才能计数,三年来实验区的试题都体现了列举法计数的重要性,有兴趣者可以继续研究往年的高考试题,此处不再赘述。
四、对教学的启示
实验区2009年高考理科卷中概率试题的上述特点对教学的启示是:
1.教学重心后移,注重概率思想的落实。
在教学中要树立教育育人的思想,不要把考试当做教育的终极目标。在概率教学中要舍得花时间让学生经历用频率估计概率的过程,让学生理解概率的意义,特别是理解不确定性数学与确定性数学的区别,体会概率的思想,这是数学史上的一大转变,也应在学生的学习生涯中留下深刻的影响,这是使学生终身受益的。
2. 创造条件,鼓励学生进行模拟实验。
在概率教学中应按照课标的要求,鼓励学生利用计算器或计算机进行模拟实验,在有条件的学校可以通过教师演示或学生操作经历模拟实验的全过程,并布置实习作业让学生进行社会实践,感受现代生活中概率的重要作用,真正理解概率。
3. 不要固守成规,要勇于改革。
对于新增加的内容,教师首先不能有排斥心理,比如几何概型;对于删减的内容教师也不要过分恋恋不舍;对于调整顺序的内容教师首先要理解其调整的原因,分析其调整是否合理,比如理科中计数原理与概率、统计三者的位置调整。在大纲教学中是将计数原理综合在概率中,课标教学中是将概率综合在计数原理中,这二者本质上没有区别,关键是教学的重心落在何处。面对这些变化,我们不应该固守成规,要与时俱进,勇于改革、科学实践。
综合上述分析,即使是为了考试取得高分也应该关注课改动向,理解并落实课标要求,如果能够为着学生的终身发展着想更应该关注概率本质的学习。
薛红霞:山西省教育科学研究院,030009.
15034088824
zhai-6@163.com
山西省教育科学研究院 薛红霞
走进高中新课程,面对教材的变化,很多老师不适应,又因为受已有教学经验的影响,在教学中有意无意地走回到大纲教材中,而且经常以“高考怎么考”为借口来佐证这种教学行为是正确的。高考怎么考,教学该怎么教?本文欲通过剖析实验区高考试题,窥探新课程概率部分的教学该怎么教。
一、课标与大纲的区别
《高中数学课程标准(实验稿)》简称课标。与大纲相比较,课标中对概率内容的设置一分为二,分别安排在数学3和选修2-3中,并调整了排列组合、统计、概率的位置。这样做是釜底抽薪,给以往在概率教学中过分注重计数的计算降温,达到突出概率本质的目的。
在大纲教材中,先学排列组合,紧接着学习概率,而且概率的学习以古典概型为主,统计则安排在选修部分。这样设置给大家的印象是:概率简单,只要分清楚几种概率模型即可,关键是要把数算对。因此概率学习、训练的重心就放在了计数上。学生对概率的理解完全是确定性数学下的套模型、计数,而没有概率思想。
课标教材改变了上述安排,先学统计(抽样、数据收集、整理、分析等),紧接着学习概率的意义、古典概型、几何概型。对于文科的学生这就是高中阶段概率学习的全部,对于理科学生将在2-3中继续学习概率和统计案例。这样安排,在概率学习的第一阶段,弱化了概率学习中的计算(没有计数工具、古典概型中也只是学习等可能事件和互斥事件的概率),强化了对概率本质的理解,尤其是基于统计学习概率,并增加了“用模拟方法(包括计算器产生随机数来进行模拟)估计概率,初步体会几何概型的意义”,如果在教学中能真正落实课标的要求,让学生经历运用计算器、计算机来处理数据,进行模拟活动的全过程,就可以让学生更好地体会统计思想和概率的意义。这样的教学才是真正具有概率思想的教学。
二、实际教学现象
面对上述变化,有些教师很不适应,在实际教学中体现为一强一弱。
强:即补充排列组合,补充的目的是为了计数方便,造成的结果是加重了学生的负担,尤其是对将来侧重文科的学生这种做法更是浪费时间,因为课标中不要求侧文的学生学习计数原理。
弱:即弱化数学3中概率的意义,忽略教材(人教A版)中整数值随机数的产生和均匀随机数的产生两节内容的学习。有的教师一带而过,有的教师采取让学生自己看书的方法敷衍了事。
这一强一弱反应出教师对课标的不理解,教学的重心放在了计数上,导致学生没有概率统计的思想,只是一个计算的奴隶。比如在我省的模块测试题中设计了如下一道试题:
甲乙两人玩一种游戏,为了研究这种游戏设计如下流程图:
(1)请你简述这种游戏的规则;
(2)假设n=1000时,k=400,求p的值.
(3)通过试验得到下列数据,根据这些数据估计甲胜的概率(精确到0.01);
次数
3000
5000
10000
20000
50000
100000
p
0.418
0.409
0.4136
0.4145
0.4185
0.41608
(4)这种游戏对甲是否公平,为什么?
(5)解释(3)、(4)两题中得到甲胜的概率值之间的关系.
这个题目基于模拟实验,旨在考查学生借助于统计整理数据,计算频率,估计概率,做出决策的全过程,并考查学生对频率与概率关系的理解。但是在解决第(3)题时有同学通过求所给各数的平均值估计概率。为什么会出现这种解法呢?是因为学生不理解统计概率思想,不确定性数学学习的思维意识差。导致这种现象的根源就是在实际教学中缺乏对统计概率思想的教学,把统计概率课上成了确定性数学中的计算课,这是统计概率教学的大忌。
三、 实验区高考试题分析
针对课标的这种变化,实验区高考如何考查概率这部分内容呢?由于侧重文科的学生不再学习计数原理,所以文科试题中的计数问题都可以通过列举法求解,此处不再具体举例。对于理科的试题,由于学生在2-3中还要学习计数原理,所以在试题中依然会出现将排列组合与概率结合考查的试题,但是这样的试题所占比重减少,而且除个别试题外,这些题目中的计数问题都比较简单。本文以2009年实验区理科9套数学试卷中的6道概率题为例进行分析。这6道题目中体现的新课程试卷的特点如下。
1. 统计概率结合,考查学生对数据的处理和运用数据决策的能力。
例1 (2009年广东理17)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间进行分组,得到频率分布直方图(如图1).
(1)求直方图中的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
(结果用分数表示.已知).
这个题目完整的考查了学生通过统计处理数据、进行决策的全过程,是具有实际使用价值的,对于学生未来的生活工作是有意义的。其中第(3)问考查互斥事件、独立重复试验的概率计算,但是在解决该问时是如下求得所需要的概率值的:该城市一年中每天空气质量为良或轻微污染的概率为,则空气质量不为良且不为轻微污染的概率为。可见这是运用频率值估计概率值,考查了概率的意义,而不是通过计数计算得出的。这种考查方式反映了课标的要求。
2. 考查模拟实验,促进学生更好的体会统计思想和概率意义。
例2 (2009福建理8)已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35 B. 0.25 C. 0.20 D. 0.15
这个题目是以模拟实验为背景命制的。题干中已经设计了模拟实验,并产生了20组模拟实验的结果。根据题意,所求的是事件“该运动员三次投篮中恰有两次命中”的概率,根据模拟实验中数字代表的含义,这个事件对应的实验结果是“三个数字中恰有两个数字是1,2,3,4中的两个”。统计所给数据可知,这20组数据中有5组符合要求,因此可以估计所求概率值为。在教学中如果认真落实了课标的要求,那么这个题目的解决就是轻车熟路,简单易行。
3. 考查新增内容,注重完整的概率过程。
例3 (2009山东理11)在区间[-1,1]上随机取一个数x,的值介于0到之间的概率为( ).
A. B. C. D. w.w.w.k.s.5.u.c.o.m
例4 (2009年辽宁理19)某人向一目标射击4次,每次击中目标的概率为。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(1)设X表示目标被击中的次数,求X的分布列;
(2)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A)。
这两个题目考查的是几何概型,例3考查的是线性测度的几何概型,例4考查的是面积测度的几何概型。关键在于这两个题目考查的是完整的几何概型问题,不是从其中截取了某一部分。实际教学中有部分教师却是把教学的重点放在了几何概型中的变换部分,认为这部分好出题,其本质还是属于确定性数学问题。通过分析这两个题目,应该认识清楚以后的教学方向。
4. 公式计数与列举法计数在计算概率时各显其优势。
例5 (2009年江苏5)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为 。
例6 (2009年安徽理10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )
A. B. C. D.
这两个题目都是考查等可能事件的概率,而且它们的共同特点是:在计算样本空间的总数时都可以借助于组合计数,但是在计算事件A所包含的基本事件的个数时都只能用列举法计数。这种考查思路可以看出,并不是一定要用排列组合才能计数,三年来实验区的试题都体现了列举法计数的重要性,有兴趣者可以继续研究往年的高考试题,此处不再赘述。
四、对教学的启示
实验区2009年高考理科卷中概率试题的上述特点对教学的启示是:
1.教学重心后移,注重概率思想的落实。
在教学中要树立教育育人的思想,不要把考试当做教育的终极目标。在概率教学中要舍得花时间让学生经历用频率估计概率的过程,让学生理解概率的意义,特别是理解不确定性数学与确定性数学的区别,体会概率的思想,这是数学史上的一大转变,也应在学生的学习生涯中留下深刻的影响,这是使学生终身受益的。
2. 创造条件,鼓励学生进行模拟实验。
在概率教学中应按照课标的要求,鼓励学生利用计算器或计算机进行模拟实验,在有条件的学校可以通过教师演示或学生操作经历模拟实验的全过程,并布置实习作业让学生进行社会实践,感受现代生活中概率的重要作用,真正理解概率。
3. 不要固守成规,要勇于改革。
对于新增加的内容,教师首先不能有排斥心理,比如几何概型;对于删减的内容教师也不要过分恋恋不舍;对于调整顺序的内容教师首先要理解其调整的原因,分析其调整是否合理,比如理科中计数原理与概率、统计三者的位置调整。在大纲教学中是将计数原理综合在概率中,课标教学中是将概率综合在计数原理中,这二者本质上没有区别,关键是教学的重心落在何处。面对这些变化,我们不应该固守成规,要与时俱进,勇于改革、科学实践。
综合上述分析,即使是为了考试取得高分也应该关注课改动向,理解并落实课标要求,如果能够为着学生的终身发展着想更应该关注概率本质的学习。
薛红霞:山西省教育科学研究院,030009.
15034088824
zhai-6@163.com
