17.1勾股定理
图片预览

文档简介
课题:§17.1 勾股定理(1课时)
教学目标:
知识与技能:探索直角三角形三边关系,了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
过程与方法:(1)、经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。(2)、在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验证”的能力,并体会数形结合和特殊到一般的思想方法。
情感态度与价值观:(1)、介绍我国古代勾股定理研究方面所取得的成就,感受数学文化,激发学生的爱国热情,促其勤奋学习。(2)、在探究活动中,培养学生的合作交流意识和探索精神。
教材分析
勾股定理是数学中几个重要定理之一,它揭示的是直角三角形边的数量关系。它在数学的发展中起着重要的作用,在现实世界中也有着广泛的应用。学生通过对勾股定理 的学习,可以在原有的基础上对直角三角形有进一步的认识和理解。
教学重点:了解勾股定理的演绎过程,掌握勾股定理及其应用。
教学难点:理解勾股定理的演绎和推导过程。
教学方法:探讨法、发现法等。
教具准备:多媒体、网格纸。
教学过程
一、创设情境——观察探索——形成概念
引入 首先创设这样一个问题情境:(用多媒体播放视频)“某楼房二楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火 ”
[设计意图及设想]问题设计具有一定的挑战性,目的是激发学生的探究欲望,教师引导学生将实际问题转化成数学问题,也就是“已知一直角三角形的两边,如何求第三边?” 的问题。学生会感到困难,从而教师指出学习了今天这一课后就有办法解决了。这种以实际问题为切入点引入新课,不仅自然,而且反映了数学来源于实际生活,数学是从人的需要中产生这一认识的基本观点。
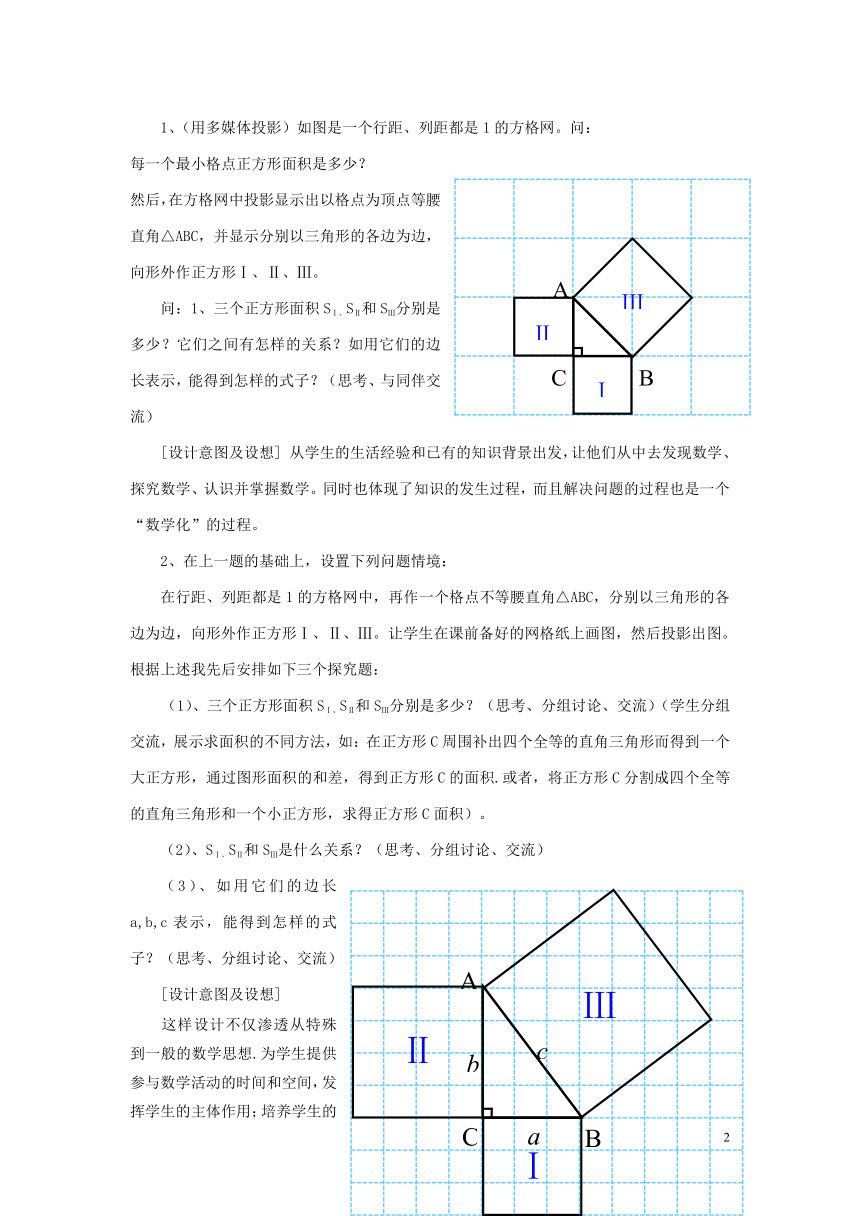
1、(用多媒体投影)如图是一个行距、列距都是1的方格网。问:
每一个最小格点正方形面积是多少?
然后,在方格网中投影显示出以格点为顶点等腰直角△ABC,并显示分别以三角形的各边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。
问:1、三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?它们之间有怎样的关系?如用它们的边长表示,能得到怎样的式子?(思考、与同伴交流)
[设计意图及设想] 从学生的生活经验和已有的知识背景出发,让他们从中去发现数学、探究数学、认识并掌握数学。同时也体现了知识的发生过程,而且解决问题的过程也是一个“数学化”的过程。
2、在上一题的基础上,设置下列问题情境:
在行距、列距都是1的方格网中,再作一个格点不等腰直角△ABC,分别以三角形的各边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。让学生在课前备好的网格纸上画图,然后投影出图。根据上述我先后安排如下三个探究题:
(1)、三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?(思考、分组讨论、交流)(学生分组交流,展示求面积的不同方法,如:在正方形C周围补出四个全等的直角三角形而得到一个大正方形,通过图形面积的和差,得到正方形C的面积.或者,将正方形C分割成四个全等的直角三角形和一个小正方形,求得正方形C面积)。
(2)、SⅠ、SⅡ和SⅢ是什么关系?(思考、分组讨论、交流)
(3)、如用它们的边长a,b,c表示,能得到怎样的式子?(思考、分组讨论、交流)
[设计意图及设想]
这样设计不仅渗透从特殊到一般的数学思想.为学生提供参与数学活动的时间和空间,发挥学生的主体作用;培养学生的类比迁移能力及探索问题的能力,使学生在相互欣赏、争辩、互助中得到提高.而且突破难点,为归纳结论打下了基础,让学生体会到观察、猜想、归纳的思想,也让学生的分析问题和解决问题的能力在无形中得到了提高,这对后面的学习及有帮助。
根据上述的问题的探究,可安排如下面探究题:你们发现直角三角形三边的长有怎样的关系?能用简练的语言概括出来吗?(学生分组讨论、小组代表发言)
结论:勾股定理 直角三角形两条直角边的平方和,等于斜边的平方。
二、创设情境——合作探究——推理论证
介绍全世界的数学家和数学爱好者都为勾股定理的证明付出过努力,使得这一定理至今有几百种证法并介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。
1、设置下列问题情境:如图在直角△ABC中,∠C=90°AB=C,BC=a, AC=b,
求证:a2+b2=c2
让学生按图示拼图。问:(1)所拼的图中,边长为C的四边形是正方形吗?为什么?
(2)让学生根据理解写出证明的推理过程。
[设计意图及设想]让学生亲身体验勾股定理的探索与验证,使学生对定理的理解更加深刻,体会数形结合思想,发展创造性思维能力.
由传统的数学课堂向实验的数学课堂转变.
2、可向学生介绍下列两种方法,激发学生的兴趣
方法二: “赵爽弦图”法.将四个全等的直角三角形拼成如图所示的正方形,
方法三:“总统”法.如图所示将两个直角三角形拼成直角梯形
以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于 . 把这两个直角三角形拼成如图所
形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,
∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90 ,
∴ ∠AED + ∠BEC = 90 .
∴ ∠DEC = 180 ―90 = 90 .
∴ ΔDEC是一个等腰直角三角形,
它的面积等于.
又∵ ∠DAE = 90 , ∠EBC = 90 ,
∴ AD∥BC.
∴ ABCD是一个直角梯形,它的面积等于.
∴ .
∴ .
以上证明方法都由学生先分组讨论获得,教师只做指导.最后总结说明。
[设计意图及设想]让学生模拟数学家的思维方式和思维过程,体会探索的快乐。
3、(定理命名).约 2000年前,代算书《周髀算经》中就记载了公元前1120年我国古人发现的“勾三股四弦五”.当时把较短的直角边叫做勾, 较长的直角边叫做股,斜边叫做弦.“勾三股四弦五”的意思是,在直角三角形中,如果勾为3,股为 4,那么弦为5.这里 .人们还发现,勾为6,股为8,那么弦一定为10.勾为5,股为12,那么弦一定为13等.所以我国称它为勾股定理.
西方国家称勾股定理为毕达哥拉斯定理。
[设计意图及设想]对学生进行爱国主义教育,增强学生的民族自豪感.
三、即时训练——巩固新知
1、课本第6页练习 第1、2、题
2、Rt△ABC的两边长分别是3和4,则第三边长的平方为多少?
3、已知等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积。
4、如图,一个3cm长的梯子,AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
思路点拨:从BD=OD-OB可以看出,必需先求OB,OD,因此,可以通过勾股定理在Rt△AOB,Rt△COD中求出OB和OD,最后将BD求出.
教师活动:制作投影仪,提出问题,引导学生观察、应用勾股定理,提问个别学生.
学生活动:观察、交流,从中寻找出Rt△AOB,Rt△COD,以此为基础应用勾股定理求得OB和OD.
[设计意图及设想]补充课堂练习,让学生对本节课的知识进行最基本的运用,为下节课勾股定理的应用做好铺垫.
四、课堂总结——提高认识
主要通过学生回忆本节课所学内容,从内容、应用、数学思想方法、获取新知的途径方面先进行小结,后由教师总结。
五、布置作业
1、课本P8 习题17.1 第1、2、3、题
2、体会本堂课你所获得成功的经验,写好数学日记,同学交流
Ⅲ
Ⅱ
Ⅰ
a
b
c
B
C
A
B
C
A
Ⅲ
Ⅱ
Ⅰ
c
b
a
c
c
c
B1
a
b
C1
F
a
b
D1
G
a
b
A1
E
H
b
c
a
C
B
A
PAGE
1
教学目标:
知识与技能:探索直角三角形三边关系,了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
过程与方法:(1)、经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。(2)、在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验证”的能力,并体会数形结合和特殊到一般的思想方法。
情感态度与价值观:(1)、介绍我国古代勾股定理研究方面所取得的成就,感受数学文化,激发学生的爱国热情,促其勤奋学习。(2)、在探究活动中,培养学生的合作交流意识和探索精神。
教材分析
勾股定理是数学中几个重要定理之一,它揭示的是直角三角形边的数量关系。它在数学的发展中起着重要的作用,在现实世界中也有着广泛的应用。学生通过对勾股定理 的学习,可以在原有的基础上对直角三角形有进一步的认识和理解。
教学重点:了解勾股定理的演绎过程,掌握勾股定理及其应用。
教学难点:理解勾股定理的演绎和推导过程。
教学方法:探讨法、发现法等。
教具准备:多媒体、网格纸。
教学过程
一、创设情境——观察探索——形成概念
引入 首先创设这样一个问题情境:(用多媒体播放视频)“某楼房二楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火 ”
[设计意图及设想]问题设计具有一定的挑战性,目的是激发学生的探究欲望,教师引导学生将实际问题转化成数学问题,也就是“已知一直角三角形的两边,如何求第三边?” 的问题。学生会感到困难,从而教师指出学习了今天这一课后就有办法解决了。这种以实际问题为切入点引入新课,不仅自然,而且反映了数学来源于实际生活,数学是从人的需要中产生这一认识的基本观点。
1、(用多媒体投影)如图是一个行距、列距都是1的方格网。问:
每一个最小格点正方形面积是多少?
然后,在方格网中投影显示出以格点为顶点等腰直角△ABC,并显示分别以三角形的各边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。
问:1、三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?它们之间有怎样的关系?如用它们的边长表示,能得到怎样的式子?(思考、与同伴交流)
[设计意图及设想] 从学生的生活经验和已有的知识背景出发,让他们从中去发现数学、探究数学、认识并掌握数学。同时也体现了知识的发生过程,而且解决问题的过程也是一个“数学化”的过程。
2、在上一题的基础上,设置下列问题情境:
在行距、列距都是1的方格网中,再作一个格点不等腰直角△ABC,分别以三角形的各边为边,向形外作正方形Ⅰ、Ⅱ、Ⅲ。让学生在课前备好的网格纸上画图,然后投影出图。根据上述我先后安排如下三个探究题:
(1)、三个正方形面积SⅠ、SⅡ和SⅢ分别是多少?(思考、分组讨论、交流)(学生分组交流,展示求面积的不同方法,如:在正方形C周围补出四个全等的直角三角形而得到一个大正方形,通过图形面积的和差,得到正方形C的面积.或者,将正方形C分割成四个全等的直角三角形和一个小正方形,求得正方形C面积)。
(2)、SⅠ、SⅡ和SⅢ是什么关系?(思考、分组讨论、交流)
(3)、如用它们的边长a,b,c表示,能得到怎样的式子?(思考、分组讨论、交流)
[设计意图及设想]
这样设计不仅渗透从特殊到一般的数学思想.为学生提供参与数学活动的时间和空间,发挥学生的主体作用;培养学生的类比迁移能力及探索问题的能力,使学生在相互欣赏、争辩、互助中得到提高.而且突破难点,为归纳结论打下了基础,让学生体会到观察、猜想、归纳的思想,也让学生的分析问题和解决问题的能力在无形中得到了提高,这对后面的学习及有帮助。
根据上述的问题的探究,可安排如下面探究题:你们发现直角三角形三边的长有怎样的关系?能用简练的语言概括出来吗?(学生分组讨论、小组代表发言)
结论:勾股定理 直角三角形两条直角边的平方和,等于斜边的平方。
二、创设情境——合作探究——推理论证
介绍全世界的数学家和数学爱好者都为勾股定理的证明付出过努力,使得这一定理至今有几百种证法并介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。
1、设置下列问题情境:如图在直角△ABC中,∠C=90°AB=C,BC=a, AC=b,
求证:a2+b2=c2
让学生按图示拼图。问:(1)所拼的图中,边长为C的四边形是正方形吗?为什么?
(2)让学生根据理解写出证明的推理过程。
[设计意图及设想]让学生亲身体验勾股定理的探索与验证,使学生对定理的理解更加深刻,体会数形结合思想,发展创造性思维能力.
由传统的数学课堂向实验的数学课堂转变.
2、可向学生介绍下列两种方法,激发学生的兴趣
方法二: “赵爽弦图”法.将四个全等的直角三角形拼成如图所示的正方形,
方法三:“总统”法.如图所示将两个直角三角形拼成直角梯形
以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于 . 把这两个直角三角形拼成如图所
形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,
∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90 ,
∴ ∠AED + ∠BEC = 90 .
∴ ∠DEC = 180 ―90 = 90 .
∴ ΔDEC是一个等腰直角三角形,
它的面积等于.
又∵ ∠DAE = 90 , ∠EBC = 90 ,
∴ AD∥BC.
∴ ABCD是一个直角梯形,它的面积等于.
∴ .
∴ .
以上证明方法都由学生先分组讨论获得,教师只做指导.最后总结说明。
[设计意图及设想]让学生模拟数学家的思维方式和思维过程,体会探索的快乐。
3、(定理命名).约 2000年前,代算书《周髀算经》中就记载了公元前1120年我国古人发现的“勾三股四弦五”.当时把较短的直角边叫做勾, 较长的直角边叫做股,斜边叫做弦.“勾三股四弦五”的意思是,在直角三角形中,如果勾为3,股为 4,那么弦为5.这里 .人们还发现,勾为6,股为8,那么弦一定为10.勾为5,股为12,那么弦一定为13等.所以我国称它为勾股定理.
西方国家称勾股定理为毕达哥拉斯定理。
[设计意图及设想]对学生进行爱国主义教育,增强学生的民族自豪感.
三、即时训练——巩固新知
1、课本第6页练习 第1、2、题
2、Rt△ABC的两边长分别是3和4,则第三边长的平方为多少?
3、已知等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积。
4、如图,一个3cm长的梯子,AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
思路点拨:从BD=OD-OB可以看出,必需先求OB,OD,因此,可以通过勾股定理在Rt△AOB,Rt△COD中求出OB和OD,最后将BD求出.
教师活动:制作投影仪,提出问题,引导学生观察、应用勾股定理,提问个别学生.
学生活动:观察、交流,从中寻找出Rt△AOB,Rt△COD,以此为基础应用勾股定理求得OB和OD.
[设计意图及设想]补充课堂练习,让学生对本节课的知识进行最基本的运用,为下节课勾股定理的应用做好铺垫.
四、课堂总结——提高认识
主要通过学生回忆本节课所学内容,从内容、应用、数学思想方法、获取新知的途径方面先进行小结,后由教师总结。
五、布置作业
1、课本P8 习题17.1 第1、2、3、题
2、体会本堂课你所获得成功的经验,写好数学日记,同学交流
Ⅲ
Ⅱ
Ⅰ
a
b
c
B
C
A
B
C
A
Ⅲ
Ⅱ
Ⅰ
c
b
a
c
c
c
B1
a
b
C1
F
a
b
D1
G
a
b
A1
E
H
b
c
a
C
B
A
PAGE
1
