29. 2. 2 三视图(2)(同步练习)(无答案)2024-2025学年九年级下册数学人教版
文档属性
| 名称 | 29. 2. 2 三视图(2)(同步练习)(无答案)2024-2025学年九年级下册数学人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 12:07:01 | ||
图片预览

文档简介
29. 2. 2 三视图(2)
旧知链接
(1) 正方体的三视图都是 .
(2) 圆柱的三视图中有两个是 ,另一个是 .
(3) 圆锥的三视图中有两个是 ,另一个是和 .
(4) 四棱锥的三视图中有两个是 ,另一个是 .
(5) 球体的三视图都是 . 新知速递
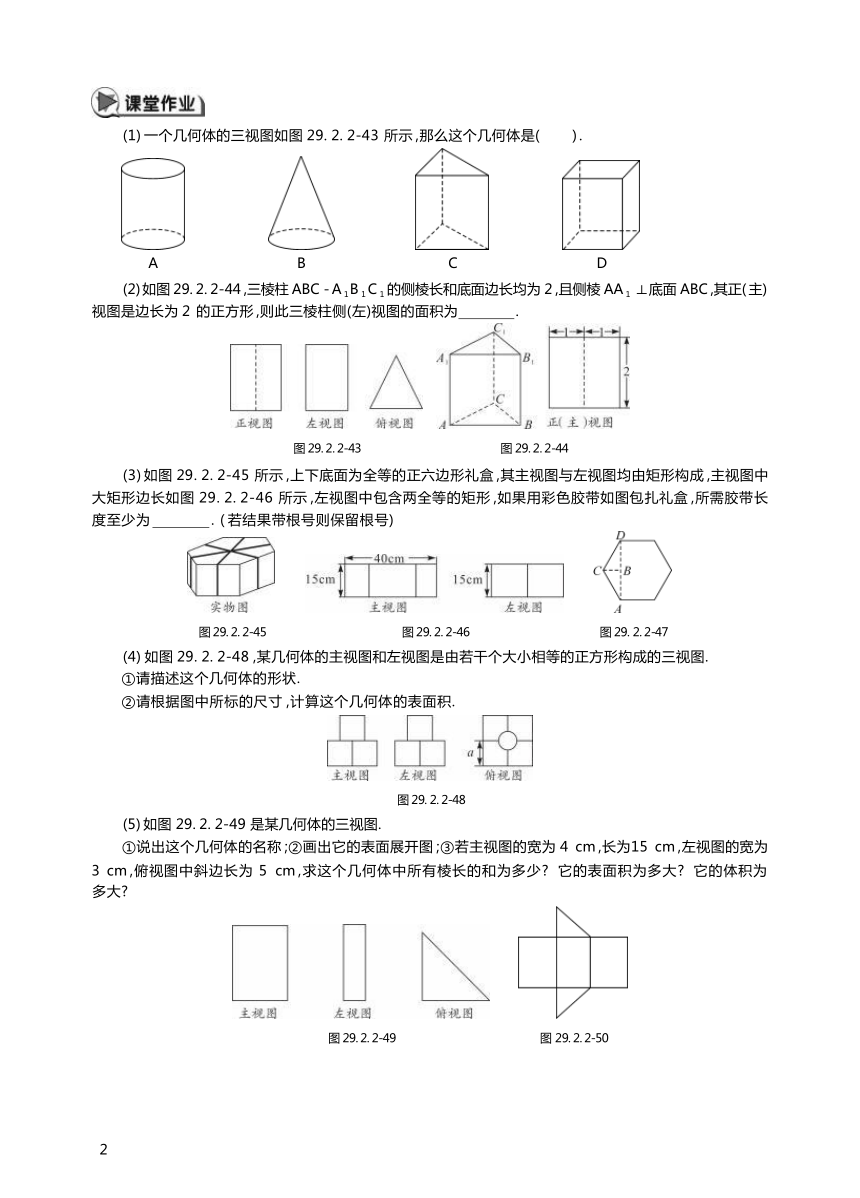
(1) 某几何体的三视图如图 29. 2. 2-38 ,则该几何体是( ) .
A. 三棱柱 B. 长方体 C. 圆柱 D. 圆锥
图 29. 2. 2-38 图 29. 2. 2-39
(2) 图 29. 2. 2-39 是某个几何体的三视图 ,该几何体是( ) .
A. 长方体 B. 三棱柱 C. 正方体 D. 圆柱
(3) 图 29. 2. 2-40 为某个几何体的三视图 ,则该几何体是( ) .
1
A
B
图 29. 2. 2-40
C
图 29. 2. 2-41
D
图 29. 2. 2-42
(4) 图 29. 2. 2-41 中三视图所对应的直观图是( ) .
A B C D
(5) 一个几何体的三视图如图 29. 2. 2-42 ,则该几何体的侧面展开图的面积为 .
(1) 一个几何体的三视图如图 29. 2. 2-43 所示 ,那么这个几何体是( ) .
A B C D
(2) 如图 29. 2. 2-44 ,三棱柱 ABC - A 1 B 1 C 1 的侧棱长和底面边长均为 2 ,且侧棱 AA 1 ⊥底面 ABC ,其正( 主) 视图是边长为 2 的正方形 ,则此三棱柱侧(左)视图的面积为 .
图 29. 2. 2-43 图 29. 2. 2-44
(3) 如图 29. 2. 2-45 所示 ,上下底面为全等的正六边形礼盒 ,其主视图与左视图均由矩形构成 ,主视图中 大矩形边长如图 29. 2. 2-46 所示 ,左视图中包含两全等的矩形 ,如果用彩色胶带如图包扎礼盒 ,所需胶带长 度至少为 . ( 若结果带根号则保留根号)
图 29. 2. 2-45 图 29. 2. 2-46 图 29. 2. 2-47
(4) 如图 29. 2. 2-48 ,某几何体的主视图和左视图是由若干个大小相等的正方形构成的三视图.
①请描述这个几何体的形状.
②请根据图中所标的尺寸 ,计算这个几何体的表面积.
图 29. 2. 2-48
(5) 如图 29. 2. 2-49 是某几何体的三视图.
①说出这个几何体的名称 ;②画出它的表面展开图 ;③若主视图的宽为 4 cm ,长为15 cm ,左视图的宽为
3 cm ,俯视图中斜边长为 5 cm ,求这个几何体中所有棱长的和为多少 它的表面积为多大 它的体积为 多大
图 29. 2. 2-49 图 29. 2. 2-50
2
基础训练
(1) 如图 29. 2. 2-51 ,一个空间几何体的主视图和左视图都是正三角形 ,俯视图是一个圆 ,那么这个几何 体是( ) .
图 29. 2. 2-51
A. 三角形 B. 三棱柱 C. 三棱锥 D. 圆锥
(2) 某几何体的三种视图如图 29. 2. 2-52 所示 ,则该几何体可能是( ) .
A. 圆锥体 B. 球体 C. 长方体 D. 圆柱体
(3) 某几何体的三视图如图 29. 2. 2-53 所示 ,则此几何体是( ) .
A. 正三棱柱 B. 圆柱 C. 长方体 D. 圆锥
图 29. 2. 2-52 图 29. 2. 2-53
(4) 一个几何体的三视图如图 29. 2. 2-54 所示 ,则这个几何体的名称是 .
(5) 如图 29. 2. 2-55 所示 , 图中是一个立体图形的三视图 ,请你根据视图 ,说出立体图形的名称 :对应的 立体图形是 的三视图.
图 29. 2. 2-54 图 29. 2. 2-55
拓展提高
(1) 学校小卖部货架上摆放着某品牌方便面 ,它们的三视图如图 29. 2. 2-56 所示 ,则货架上的方便面至
少有 盒.
图 29. 2. 2-56 图 29. 2. 2-57
(2) 已知一个几何体的三视图和有关的尺寸如图 29. 2. 2-57 所示 ,请写出该几何体的名称 ,并根据图中 所给的数据求出它的表面积和体积.
3
(3) 如图 29. 2. 2-58 所示是某种型号的正六角螺母毛坯的三视图 ,求它的表面积.
图 29. 2. 2-58
发散思维
(1) 下列给出了某种工件的三视图如图 29. 2. 2-59 ,某工厂要铸造 5000 件这种铁质工件 ,要用去多少吨 生铁工件铸成后 ,表面需得涂一层防锈漆 ,已知 1 千克防锈漆可以涂 4 m 2 的铁器面 ,涂完这批工件要用多少 千克防锈漆 (铁的比重为 7. 8g/cm 3 ,单位为 cm)
图 29. 2. 2-59
(2) 如图 29. 2. 2-60 是一个几何体的三视图.
①写出这个几何体的名称.
②根据所示数据计算这个几何体的表面积.
③如果一只蚂蚁要从这个几何体中的点 B 出发 ,沿表面爬到 AC 的中点 D ,请你求出这个线路的最短 路程.
图 29. 2. 2-60
4
旧知链接
(1) 正方体的三视图都是 .
(2) 圆柱的三视图中有两个是 ,另一个是 .
(3) 圆锥的三视图中有两个是 ,另一个是和 .
(4) 四棱锥的三视图中有两个是 ,另一个是 .
(5) 球体的三视图都是 . 新知速递
(1) 某几何体的三视图如图 29. 2. 2-38 ,则该几何体是( ) .
A. 三棱柱 B. 长方体 C. 圆柱 D. 圆锥
图 29. 2. 2-38 图 29. 2. 2-39
(2) 图 29. 2. 2-39 是某个几何体的三视图 ,该几何体是( ) .
A. 长方体 B. 三棱柱 C. 正方体 D. 圆柱
(3) 图 29. 2. 2-40 为某个几何体的三视图 ,则该几何体是( ) .
1
A
B
图 29. 2. 2-40
C
图 29. 2. 2-41
D
图 29. 2. 2-42
(4) 图 29. 2. 2-41 中三视图所对应的直观图是( ) .
A B C D
(5) 一个几何体的三视图如图 29. 2. 2-42 ,则该几何体的侧面展开图的面积为 .
(1) 一个几何体的三视图如图 29. 2. 2-43 所示 ,那么这个几何体是( ) .
A B C D
(2) 如图 29. 2. 2-44 ,三棱柱 ABC - A 1 B 1 C 1 的侧棱长和底面边长均为 2 ,且侧棱 AA 1 ⊥底面 ABC ,其正( 主) 视图是边长为 2 的正方形 ,则此三棱柱侧(左)视图的面积为 .
图 29. 2. 2-43 图 29. 2. 2-44
(3) 如图 29. 2. 2-45 所示 ,上下底面为全等的正六边形礼盒 ,其主视图与左视图均由矩形构成 ,主视图中 大矩形边长如图 29. 2. 2-46 所示 ,左视图中包含两全等的矩形 ,如果用彩色胶带如图包扎礼盒 ,所需胶带长 度至少为 . ( 若结果带根号则保留根号)
图 29. 2. 2-45 图 29. 2. 2-46 图 29. 2. 2-47
(4) 如图 29. 2. 2-48 ,某几何体的主视图和左视图是由若干个大小相等的正方形构成的三视图.
①请描述这个几何体的形状.
②请根据图中所标的尺寸 ,计算这个几何体的表面积.
图 29. 2. 2-48
(5) 如图 29. 2. 2-49 是某几何体的三视图.
①说出这个几何体的名称 ;②画出它的表面展开图 ;③若主视图的宽为 4 cm ,长为15 cm ,左视图的宽为
3 cm ,俯视图中斜边长为 5 cm ,求这个几何体中所有棱长的和为多少 它的表面积为多大 它的体积为 多大
图 29. 2. 2-49 图 29. 2. 2-50
2
基础训练
(1) 如图 29. 2. 2-51 ,一个空间几何体的主视图和左视图都是正三角形 ,俯视图是一个圆 ,那么这个几何 体是( ) .
图 29. 2. 2-51
A. 三角形 B. 三棱柱 C. 三棱锥 D. 圆锥
(2) 某几何体的三种视图如图 29. 2. 2-52 所示 ,则该几何体可能是( ) .
A. 圆锥体 B. 球体 C. 长方体 D. 圆柱体
(3) 某几何体的三视图如图 29. 2. 2-53 所示 ,则此几何体是( ) .
A. 正三棱柱 B. 圆柱 C. 长方体 D. 圆锥
图 29. 2. 2-52 图 29. 2. 2-53
(4) 一个几何体的三视图如图 29. 2. 2-54 所示 ,则这个几何体的名称是 .
(5) 如图 29. 2. 2-55 所示 , 图中是一个立体图形的三视图 ,请你根据视图 ,说出立体图形的名称 :对应的 立体图形是 的三视图.
图 29. 2. 2-54 图 29. 2. 2-55
拓展提高
(1) 学校小卖部货架上摆放着某品牌方便面 ,它们的三视图如图 29. 2. 2-56 所示 ,则货架上的方便面至
少有 盒.
图 29. 2. 2-56 图 29. 2. 2-57
(2) 已知一个几何体的三视图和有关的尺寸如图 29. 2. 2-57 所示 ,请写出该几何体的名称 ,并根据图中 所给的数据求出它的表面积和体积.
3
(3) 如图 29. 2. 2-58 所示是某种型号的正六角螺母毛坯的三视图 ,求它的表面积.
图 29. 2. 2-58
发散思维
(1) 下列给出了某种工件的三视图如图 29. 2. 2-59 ,某工厂要铸造 5000 件这种铁质工件 ,要用去多少吨 生铁工件铸成后 ,表面需得涂一层防锈漆 ,已知 1 千克防锈漆可以涂 4 m 2 的铁器面 ,涂完这批工件要用多少 千克防锈漆 (铁的比重为 7. 8g/cm 3 ,单位为 cm)
图 29. 2. 2-59
(2) 如图 29. 2. 2-60 是一个几何体的三视图.
①写出这个几何体的名称.
②根据所示数据计算这个几何体的表面积.
③如果一只蚂蚁要从这个几何体中的点 B 出发 ,沿表面爬到 AC 的中点 D ,请你求出这个线路的最短 路程.
图 29. 2. 2-60
4
