27. 2. 3 相似三角形应用举例 同步练习(无答案)2024-2025学年九年级下册数学人教版
文档属性
| 名称 | 27. 2. 3 相似三角形应用举例 同步练习(无答案)2024-2025学年九年级下册数学人教版 | 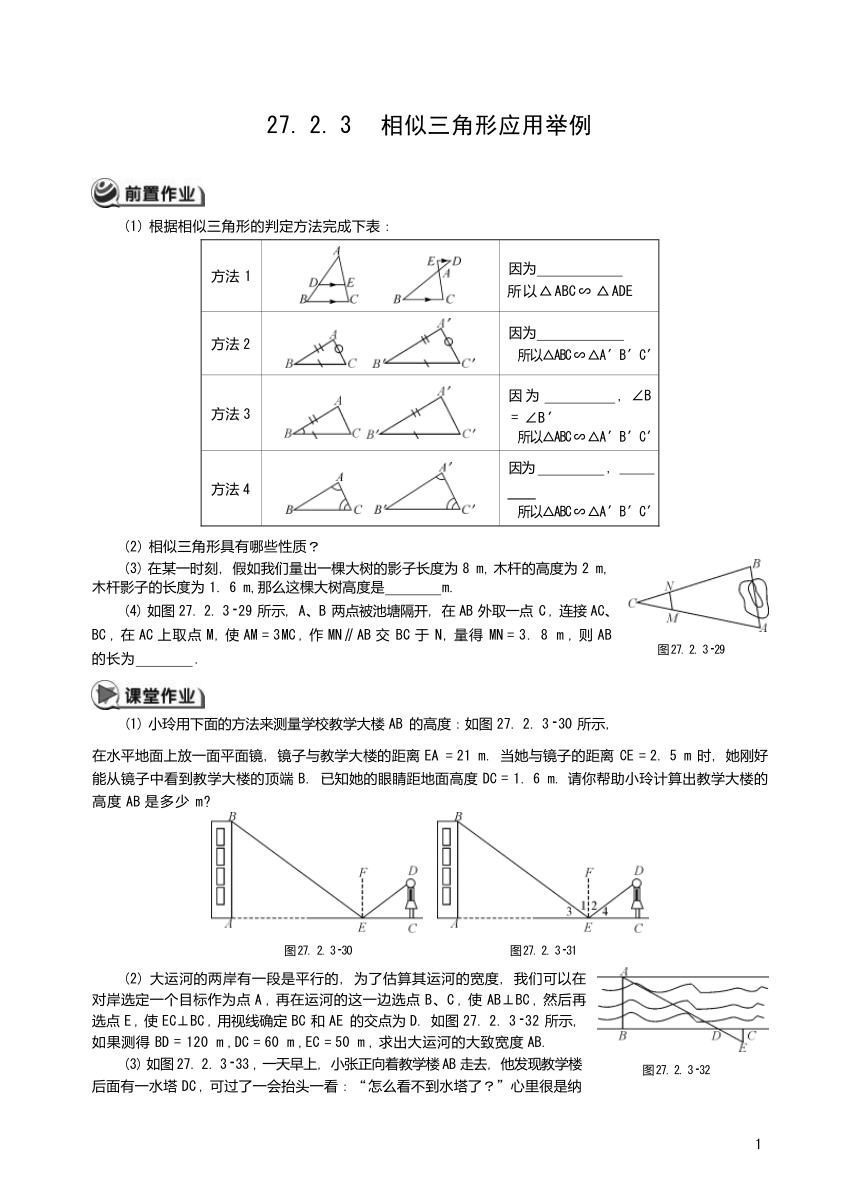 | |
| 格式 | docx | ||
| 文件大小 | 92.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 18:04:36 | ||
图片预览

文档简介
27. 2. 3 相似三角形应用举例
(1) 根据相似三角形的判定方法完成下表:
方法 1 因为 所以△ABC ∽ △ADE
方法 2 因为 所以△ABC ∽ △A ′B ′C ′
方法 3 因 为 ,∠B = ∠B ′ 所以△ABC ∽ △A ′B ′C ′
方法 4 因为 , 所以△ABC ∽ △A ′B ′C ′
1
(2) 相似三角形具有哪些性质?
(3) 在某一时刻,假如我们量出一棵大树的影子长度为 8 m, 木杆的高度为 2 m, 木杆影子的长度为 1. 6 m,那么这棵大树高度是 m.
(4) 如图 27. 2. 3 29 所示,A、B 两点被池塘隔开,在 AB 外取一点 C , 连接 AC、 BC , 在 AC 上取点 M, 使 AM = 3MC , 作 MN∥AB 交 BC 于 N, 量得 MN = 3. 8 m , 则 AB 的长为 .
(1) 小玲用下面的方法来测量学校教学大楼 AB 的高度:如图 27. 2. 3 30 所示,
图 27. 2. 3 29
在水平地面上放一面平面镜,镜子与教学大楼的距离 EA = 21 m. 当她与镜子的距离 CE = 2. 5 m 时,她刚好 能从镜子中看到教学大楼的顶端 B. 已知她的眼睛距地面高度 DC = 1. 6 m. 请你帮助小玲计算出教学大楼的 高度 AB 是多少 m
图 27. 2. 3 30 图 27. 2. 3 31
(2) 大运河的两岸有一段是平行的,为了估算其运河的宽度,我们可以在 对岸选定一个目标作为点 A , 再在运河的这一边选点 B、C , 使 AB⊥BC , 然后再 选点 E , 使 EC⊥BC , 用视线确定 BC 和 AE 的交点为 D. 如图 27. 2. 3 32 所示, 如果测得 BD = 120 m ,DC = 60 m ,EC = 50 m , 求出大运河的大致宽度 AB.
(3) 如图 27. 2. 3 33 , 一天早上,小张正向着教学楼 AB 走去,他发现教学楼 后面有一水塔 DC , 可过了一会抬头一看:“ 怎么看不到水塔了?”心里很是纳
图 27. 2. 3 32
闷.经过了解,教学楼、水塔的高分别为 20 m 和30 m , 它们之间的距离为 30 m , 小张身高为 1. 6 m( 眼睛到头 顶的距离忽略不计).小张要想看到水塔,他与教学楼的距离至少应有多少米?
2
图 27. 2. 3 33
图 27. 2. 3 34
基础训练
(1) 小明身高 1. 5 m , 在操场的影长为 2 m , 同时测得教学大楼在操场的影长为 60 m , 则教学大楼的高度 应为( ) .
A. 45 m B. 40 m C. 90 m D. 80 m
(2) 如图 27. 2. 3 35 所示,当小颖从路灯 AB 的底部 A 点走到 C 点时,发现自己在路灯 B 下的影子顶部 落在正前方 E 处.若 AC = 4 m , 影子 CE = 2 m , 小颖身高为 1. 6 m , 则路灯 AB 的高为( ) .
A. 4. 8 m B. 4 m C. 3. 2 m D. 2. 4 m
(3) 如图 27. 2. 3 36 所示,铁路道口的栏杆短臂长 1 m , 长臂长 16 m. 当短臂端点下降0. 5 m时,长臂端点 升高(杆的宽度忽略不计)( ) .
A. 4 m B. 6 m C. 8 m D. 12 m
(4) 如图 27. 2. 3 37 所示,小明同学用自制的直角三角形纸板 DEF 测量树的高度 AB , 他调整自己的位 置,设法使斜边 DF 保持水平,并且边 DE 与点B 在同一直线上.已知纸板的两条直角边 DE = 40 cm,EF = 20 cm,测得边 DF 离地面的高度 AC = 1. 5 m, CD = 8 m,则树高AB = m.
图 27. 2. 3 35 图 27. 2. 3 36 图 27. 2. 3 37
(5) 如图 27. 2. 3 38 所示,阳光从教室的窗户射入室内,窗户框 AB 在地面上的影长 DE = 1. 8 m, 窗户下檐 到地面的距离 BC = 1 m,EC = 1. 2 m,那么窗户的高 AB 为 m.
图 27. 2. 3 38
拓展提高
(1) 教学楼旁边有一棵树,课外数学兴趣小组在阳光下测得一根长为 1 m 的竹竿的影长为 0. 9 m , 他们 马上测树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图 27. 2. 3 39 所示,经 过一番争论,该小组的同学认为继续测量也可以求出树高,他们测得落在地面上的影长为 2. 7 m , 落在墙壁 上的影长为 1. 2 m ,请你和他们一起计算一下树高.
图 27. 2. 3 39
(2) 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯 D 的高度.如图 27. 2. 3 40 , 当李明走到点 A 处时,张龙测得李明直立时身高 AM 与影子长 AE 正好相等;接着李明沿 AC 方向继续向前走,走到点 B 处 时,李明直立时身高 BN 的影子恰好是线段 AB , 并测得 AB = 1. 25 m , 已知李明直立时的身高为 1. 75 m , 求路
灯的高 CD 的长.(结果精确到 0. 1 m)
图 27. 2. 3 40
(3) 如图 27. 2. 1 41 所示,小华家(点A 处)和公路( l) 之间竖立着一块 30m 长且平行于公路的巨型广告 牌( DE) , 广告牌挡住了小华的视线,请在图中画出视点 A 的盲区,并将盲区的那段公路记 BC , 一辆以 60km/ h 匀速行驶的汽车经过公路 BC 段的时间为 6 秒,已知广告牌和公路的距离为 35m , 求小华家到公路的距离.
图 27. 2. 3 41
发散思维
(1) 如图 27. 2. 3 42 所示,已知:CD 为一幢 3m 高的温室,其南面窗户的底框 G 距地面 1m , CD 在地面上 留下的最大影长 CF 为 2m , 现欲在距 C 点 7m 的正南方 A 点处建一幢 12m 高的楼房 AB(设 A , C , F 在同一水 平线上).
①按比例较精确地做出高楼 AB 及它的最大影长 AE.
②问若大楼 AB 建成后是否影响温室 CD 的采光,试说明理由.
图 27. 2. 3 42
(2) 汪老师要装修自己带阁楼的新居(图 27. 2. 3 43 为新居剖面图),在建造客厅到阁楼的楼梯 AC 时,为避 免上楼时墙角 F 碰头,设计墙角F 到楼梯的竖直距离 FG 为 1. 75 m. 他量得客厅高 AB = 2. 8 m, 楼梯洞口宽 AF = 2 m. 阁楼阳台宽 EF = 3 m. 请你帮助汪老师解决下列问题:
①要使墙角 F 到楼梯的竖直距离 FG 为 1. 75 m , 楼梯底端 C 到墙角 D 的距离 CD 是多少 m
②在①的条件下,为保证上楼时的舒适感,楼梯的每个台阶小于 20 cm , 每个台阶宽要大于 20 cm , 问汪 老师应该将楼梯建几个台阶? 为什么?
图 27. 2. 3 43
3
(1) 根据相似三角形的判定方法完成下表:
方法 1 因为 所以△ABC ∽ △ADE
方法 2 因为 所以△ABC ∽ △A ′B ′C ′
方法 3 因 为 ,∠B = ∠B ′ 所以△ABC ∽ △A ′B ′C ′
方法 4 因为 , 所以△ABC ∽ △A ′B ′C ′
1
(2) 相似三角形具有哪些性质?
(3) 在某一时刻,假如我们量出一棵大树的影子长度为 8 m, 木杆的高度为 2 m, 木杆影子的长度为 1. 6 m,那么这棵大树高度是 m.
(4) 如图 27. 2. 3 29 所示,A、B 两点被池塘隔开,在 AB 外取一点 C , 连接 AC、 BC , 在 AC 上取点 M, 使 AM = 3MC , 作 MN∥AB 交 BC 于 N, 量得 MN = 3. 8 m , 则 AB 的长为 .
(1) 小玲用下面的方法来测量学校教学大楼 AB 的高度:如图 27. 2. 3 30 所示,
图 27. 2. 3 29
在水平地面上放一面平面镜,镜子与教学大楼的距离 EA = 21 m. 当她与镜子的距离 CE = 2. 5 m 时,她刚好 能从镜子中看到教学大楼的顶端 B. 已知她的眼睛距地面高度 DC = 1. 6 m. 请你帮助小玲计算出教学大楼的 高度 AB 是多少 m
图 27. 2. 3 30 图 27. 2. 3 31
(2) 大运河的两岸有一段是平行的,为了估算其运河的宽度,我们可以在 对岸选定一个目标作为点 A , 再在运河的这一边选点 B、C , 使 AB⊥BC , 然后再 选点 E , 使 EC⊥BC , 用视线确定 BC 和 AE 的交点为 D. 如图 27. 2. 3 32 所示, 如果测得 BD = 120 m ,DC = 60 m ,EC = 50 m , 求出大运河的大致宽度 AB.
(3) 如图 27. 2. 3 33 , 一天早上,小张正向着教学楼 AB 走去,他发现教学楼 后面有一水塔 DC , 可过了一会抬头一看:“ 怎么看不到水塔了?”心里很是纳
图 27. 2. 3 32
闷.经过了解,教学楼、水塔的高分别为 20 m 和30 m , 它们之间的距离为 30 m , 小张身高为 1. 6 m( 眼睛到头 顶的距离忽略不计).小张要想看到水塔,他与教学楼的距离至少应有多少米?
2
图 27. 2. 3 33
图 27. 2. 3 34
基础训练
(1) 小明身高 1. 5 m , 在操场的影长为 2 m , 同时测得教学大楼在操场的影长为 60 m , 则教学大楼的高度 应为( ) .
A. 45 m B. 40 m C. 90 m D. 80 m
(2) 如图 27. 2. 3 35 所示,当小颖从路灯 AB 的底部 A 点走到 C 点时,发现自己在路灯 B 下的影子顶部 落在正前方 E 处.若 AC = 4 m , 影子 CE = 2 m , 小颖身高为 1. 6 m , 则路灯 AB 的高为( ) .
A. 4. 8 m B. 4 m C. 3. 2 m D. 2. 4 m
(3) 如图 27. 2. 3 36 所示,铁路道口的栏杆短臂长 1 m , 长臂长 16 m. 当短臂端点下降0. 5 m时,长臂端点 升高(杆的宽度忽略不计)( ) .
A. 4 m B. 6 m C. 8 m D. 12 m
(4) 如图 27. 2. 3 37 所示,小明同学用自制的直角三角形纸板 DEF 测量树的高度 AB , 他调整自己的位 置,设法使斜边 DF 保持水平,并且边 DE 与点B 在同一直线上.已知纸板的两条直角边 DE = 40 cm,EF = 20 cm,测得边 DF 离地面的高度 AC = 1. 5 m, CD = 8 m,则树高AB = m.
图 27. 2. 3 35 图 27. 2. 3 36 图 27. 2. 3 37
(5) 如图 27. 2. 3 38 所示,阳光从教室的窗户射入室内,窗户框 AB 在地面上的影长 DE = 1. 8 m, 窗户下檐 到地面的距离 BC = 1 m,EC = 1. 2 m,那么窗户的高 AB 为 m.
图 27. 2. 3 38
拓展提高
(1) 教学楼旁边有一棵树,课外数学兴趣小组在阳光下测得一根长为 1 m 的竹竿的影长为 0. 9 m , 他们 马上测树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图 27. 2. 3 39 所示,经 过一番争论,该小组的同学认为继续测量也可以求出树高,他们测得落在地面上的影长为 2. 7 m , 落在墙壁 上的影长为 1. 2 m ,请你和他们一起计算一下树高.
图 27. 2. 3 39
(2) 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯 D 的高度.如图 27. 2. 3 40 , 当李明走到点 A 处时,张龙测得李明直立时身高 AM 与影子长 AE 正好相等;接着李明沿 AC 方向继续向前走,走到点 B 处 时,李明直立时身高 BN 的影子恰好是线段 AB , 并测得 AB = 1. 25 m , 已知李明直立时的身高为 1. 75 m , 求路
灯的高 CD 的长.(结果精确到 0. 1 m)
图 27. 2. 3 40
(3) 如图 27. 2. 1 41 所示,小华家(点A 处)和公路( l) 之间竖立着一块 30m 长且平行于公路的巨型广告 牌( DE) , 广告牌挡住了小华的视线,请在图中画出视点 A 的盲区,并将盲区的那段公路记 BC , 一辆以 60km/ h 匀速行驶的汽车经过公路 BC 段的时间为 6 秒,已知广告牌和公路的距离为 35m , 求小华家到公路的距离.
图 27. 2. 3 41
发散思维
(1) 如图 27. 2. 3 42 所示,已知:CD 为一幢 3m 高的温室,其南面窗户的底框 G 距地面 1m , CD 在地面上 留下的最大影长 CF 为 2m , 现欲在距 C 点 7m 的正南方 A 点处建一幢 12m 高的楼房 AB(设 A , C , F 在同一水 平线上).
①按比例较精确地做出高楼 AB 及它的最大影长 AE.
②问若大楼 AB 建成后是否影响温室 CD 的采光,试说明理由.
图 27. 2. 3 42
(2) 汪老师要装修自己带阁楼的新居(图 27. 2. 3 43 为新居剖面图),在建造客厅到阁楼的楼梯 AC 时,为避 免上楼时墙角 F 碰头,设计墙角F 到楼梯的竖直距离 FG 为 1. 75 m. 他量得客厅高 AB = 2. 8 m, 楼梯洞口宽 AF = 2 m. 阁楼阳台宽 EF = 3 m. 请你帮助汪老师解决下列问题:
①要使墙角 F 到楼梯的竖直距离 FG 为 1. 75 m , 楼梯底端 C 到墙角 D 的距离 CD 是多少 m
②在①的条件下,为保证上楼时的舒适感,楼梯的每个台阶小于 20 cm , 每个台阶宽要大于 20 cm , 问汪 老师应该将楼梯建几个台阶? 为什么?
图 27. 2. 3 43
3
