27. 3. 1 位似(1)同步练习(无答案)2024-2025学年九年级下册数学人教版
文档属性
| 名称 | 27. 3. 1 位似(1)同步练习(无答案)2024-2025学年九年级下册数学人教版 | 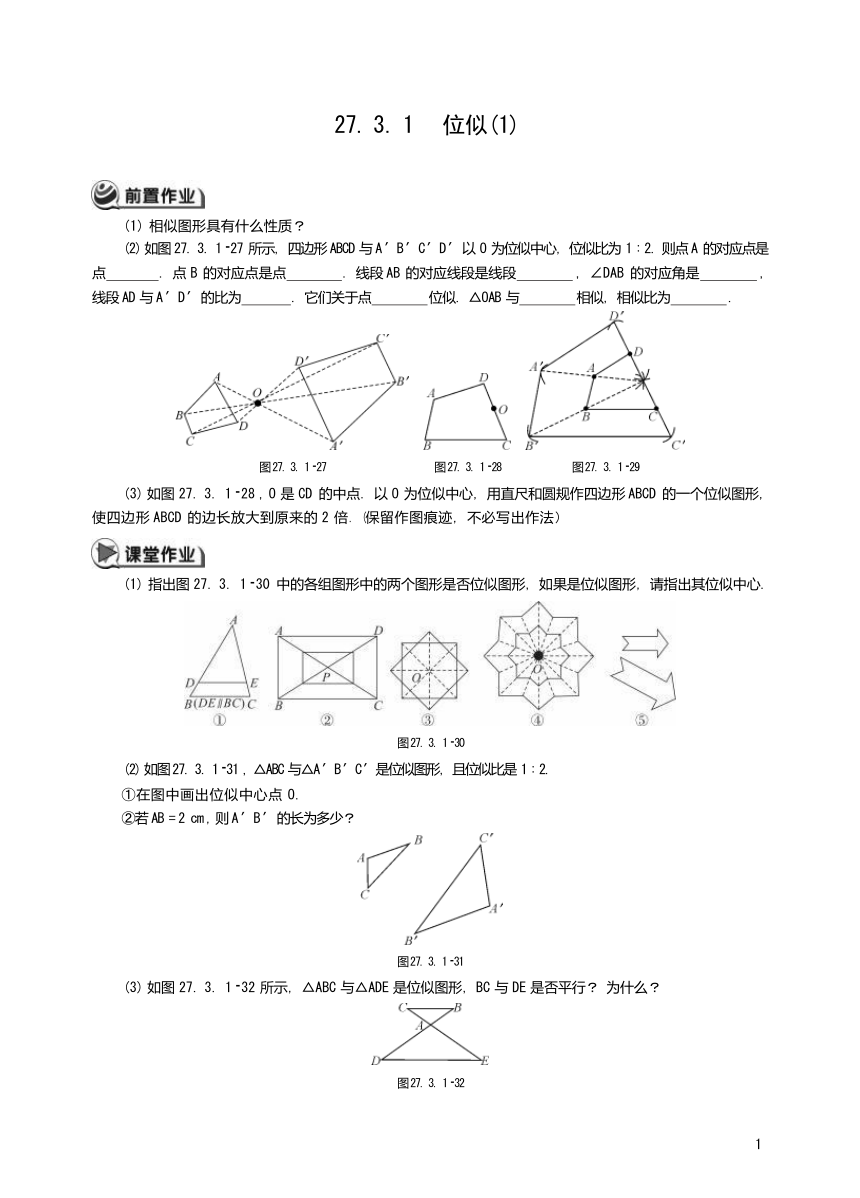 | |
| 格式 | docx | ||
| 文件大小 | 105.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 18:05:00 | ||
图片预览

文档简介
27. 3. 1 位似(1)
(1) 相似图形具有什么性质?
(2) 如图 27. 3. 1 27 所示,四边形 ABCD 与 A ′B ′C ′D ′ 以 O 为位似中心,位似比为 1 ∶ 2. 则点 A 的对应点是 点 .点 B 的对应点是点 .线段 AB 的对应线段是线段 ,∠DAB 的对应角是 , 线段 AD 与 A ′D ′ 的比为 .它们关于点 位似. △OAB 与 相似,相似比为 .
图 27. 3. 1 27 图 27. 3. 1 28 图 27. 3. 1 29
(3) 如图 27. 3. 1 28 , O 是 CD 的中点.以 O 为位似中心,用直尺和圆规作四边形 ABCD 的一个位似图形, 使四边形 ABCD 的边长放大到原来的 2 倍.(保留作图痕迹,不必写出作法)
(1) 指出图 27. 3. 1 30 中的各组图形中的两个图形是否位似图形,如果是位似图形,请指出其位似中心.
图 27. 3. 1 30
(2) 如图 27. 3. 1 31 , △ABC 与△A ′B ′C ′是位似图形,且位似比是 1 ∶ 2.
①在图中画出位似中心点 O.
②若 AB = 2 cm , 则 A ′B ′ 的长为多少?
图 27. 3. 1 31
(3) 如图 27. 3. 1 32 所示,△ABC 与△ADE 是位似图形,BC 与 DE 是否平行? 为什么?
图 27. 3. 1 32
1
(4) 已知四边形 ABCD 及点 O ,试以点 O 为位似中心,将如图 27. 3. 1 33 所示的四个四边形放大为原来
的 2 倍.
图 27. 3. 1 33
基础训练
(1) 如图 27. 3. 1 36 , 已知△EFH 和△MNK 是位似图形,那么其位似中心是( ) .
A. 点 A B. 点 B C. 点 C D. 点 D
图 27. 3. 1 36
(2) 如图 27. 3. 1 37 , △ABC 与△DEF 是位似图形,O 是位似中心,OA = AD , 则△ABC 与△DEF 的位似比 是( ) .
A. B. C. 2 D. 3
(3) 如图 27. 3. 1 38 , 位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶ 5 , 且三角尺的一 边长为 8 cm , 则投影三角形的对应边长为( ) .
A. 8 cm B. 20 cm C. 3. 2 cm D. 10 cm
(4) 如图 27. 3. 1 39 , 矩形 ABCD 中,对角线 AC、BD 相交于点 O , 点 E、F、G、H 分别是 AO、BO、CO、DO 的 中点,连接 EF、FG、GH、EH, 则下列说法不正确的是( ) .
A. △OEF 和△OAB 是位似图形 B. △OEH 和△OFG 是位似图形
C. △EFH 和△ABD 是位似图形 D. △OHG 和△OGF 是位似图形
图 27. 3. 1 37 图 27. 3. 1 38 图 27. 3. 1 39
(5) 找出如图 27. 3. 1 40 所示的各图形的位似中心.
(
图
27.
3. 1
40
)
2
(6) 如图 27. 3. 1 41 , 分别按下列要求作出四边形 ABCD 以 D 点为位似中心的位似四 边形 A ′B ′C ′D ′.
①沿 OA 方向放大为原图的 2 倍.
②沿 AO 的方向放大为原图的 2 倍.
图 27. 3. 1 41
拓展提高
(1) 如图 27. 3. 1 42 , △ACC ′是由△ABB ′经过位似变换得到的.
①求出△ACC ′与△ABB ′ 的相似比,并指出它们的位似中心.
②△AEE ′是△ABB ′ 的位似图形吗? 如果是,求相似比;如果不是,说明理由.
③如果相似比为 3 , 那么△ABB ′ 的位似图形是什么?
(2) 如图 27. 3. 1 43 所示的① ~ ④是几组三角形的组合图形,图① 中,△AOB ∽ △DOC; 图②中,△ABC ∽ △ADE; 图③中,△ABC ∽ △ACD; 图④中,△ACD ∽ △CBD.
小 Q 说:图①②是位似变换,其位似中心分别是 O 和 A. 小 R 说:图③④是位似变换,其位似中心是点 D.
请你观察一番,评判小 Q、小 R 谁对谁错,并说明原因.
图 27. 3. 1 42
3
图 27. 3. 1 43 图 27. 3. 1 44
发散思维
(1) 如图 27. 3. 1 44 , 点 E , F 分别是 ABCD 的 AB 边和 CD 边延长线上的点,连接 EF 交 AD ,BC 于点 H, G, 则图中的位似图形有 .(至少写出两对)
(2) 如图27. 3. 1 45 , △ABC 中,AB = 80 cm , 高 CD = 60 cm , 矩形 EFGH 中 E、F 在 AB 边上,G 在 BC 边上, H 在三角形内,且 EF∶ GF = 2∶ 1.
①在△ABC 内画出矩形 GFEH 的位似形,使其顶点在△ABC 的边上.(保留作图痕迹)
②求所作的矩形的面积.
图 27. 3. 1 45
(1) 相似图形具有什么性质?
(2) 如图 27. 3. 1 27 所示,四边形 ABCD 与 A ′B ′C ′D ′ 以 O 为位似中心,位似比为 1 ∶ 2. 则点 A 的对应点是 点 .点 B 的对应点是点 .线段 AB 的对应线段是线段 ,∠DAB 的对应角是 , 线段 AD 与 A ′D ′ 的比为 .它们关于点 位似. △OAB 与 相似,相似比为 .
图 27. 3. 1 27 图 27. 3. 1 28 图 27. 3. 1 29
(3) 如图 27. 3. 1 28 , O 是 CD 的中点.以 O 为位似中心,用直尺和圆规作四边形 ABCD 的一个位似图形, 使四边形 ABCD 的边长放大到原来的 2 倍.(保留作图痕迹,不必写出作法)
(1) 指出图 27. 3. 1 30 中的各组图形中的两个图形是否位似图形,如果是位似图形,请指出其位似中心.
图 27. 3. 1 30
(2) 如图 27. 3. 1 31 , △ABC 与△A ′B ′C ′是位似图形,且位似比是 1 ∶ 2.
①在图中画出位似中心点 O.
②若 AB = 2 cm , 则 A ′B ′ 的长为多少?
图 27. 3. 1 31
(3) 如图 27. 3. 1 32 所示,△ABC 与△ADE 是位似图形,BC 与 DE 是否平行? 为什么?
图 27. 3. 1 32
1
(4) 已知四边形 ABCD 及点 O ,试以点 O 为位似中心,将如图 27. 3. 1 33 所示的四个四边形放大为原来
的 2 倍.
图 27. 3. 1 33
基础训练
(1) 如图 27. 3. 1 36 , 已知△EFH 和△MNK 是位似图形,那么其位似中心是( ) .
A. 点 A B. 点 B C. 点 C D. 点 D
图 27. 3. 1 36
(2) 如图 27. 3. 1 37 , △ABC 与△DEF 是位似图形,O 是位似中心,OA = AD , 则△ABC 与△DEF 的位似比 是( ) .
A. B. C. 2 D. 3
(3) 如图 27. 3. 1 38 , 位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶ 5 , 且三角尺的一 边长为 8 cm , 则投影三角形的对应边长为( ) .
A. 8 cm B. 20 cm C. 3. 2 cm D. 10 cm
(4) 如图 27. 3. 1 39 , 矩形 ABCD 中,对角线 AC、BD 相交于点 O , 点 E、F、G、H 分别是 AO、BO、CO、DO 的 中点,连接 EF、FG、GH、EH, 则下列说法不正确的是( ) .
A. △OEF 和△OAB 是位似图形 B. △OEH 和△OFG 是位似图形
C. △EFH 和△ABD 是位似图形 D. △OHG 和△OGF 是位似图形
图 27. 3. 1 37 图 27. 3. 1 38 图 27. 3. 1 39
(5) 找出如图 27. 3. 1 40 所示的各图形的位似中心.
(
图
27.
3. 1
40
)
2
(6) 如图 27. 3. 1 41 , 分别按下列要求作出四边形 ABCD 以 D 点为位似中心的位似四 边形 A ′B ′C ′D ′.
①沿 OA 方向放大为原图的 2 倍.
②沿 AO 的方向放大为原图的 2 倍.
图 27. 3. 1 41
拓展提高
(1) 如图 27. 3. 1 42 , △ACC ′是由△ABB ′经过位似变换得到的.
①求出△ACC ′与△ABB ′ 的相似比,并指出它们的位似中心.
②△AEE ′是△ABB ′ 的位似图形吗? 如果是,求相似比;如果不是,说明理由.
③如果相似比为 3 , 那么△ABB ′ 的位似图形是什么?
(2) 如图 27. 3. 1 43 所示的① ~ ④是几组三角形的组合图形,图① 中,△AOB ∽ △DOC; 图②中,△ABC ∽ △ADE; 图③中,△ABC ∽ △ACD; 图④中,△ACD ∽ △CBD.
小 Q 说:图①②是位似变换,其位似中心分别是 O 和 A. 小 R 说:图③④是位似变换,其位似中心是点 D.
请你观察一番,评判小 Q、小 R 谁对谁错,并说明原因.
图 27. 3. 1 42
3
图 27. 3. 1 43 图 27. 3. 1 44
发散思维
(1) 如图 27. 3. 1 44 , 点 E , F 分别是 ABCD 的 AB 边和 CD 边延长线上的点,连接 EF 交 AD ,BC 于点 H, G, 则图中的位似图形有 .(至少写出两对)
(2) 如图27. 3. 1 45 , △ABC 中,AB = 80 cm , 高 CD = 60 cm , 矩形 EFGH 中 E、F 在 AB 边上,G 在 BC 边上, H 在三角形内,且 EF∶ GF = 2∶ 1.
①在△ABC 内画出矩形 GFEH 的位似形,使其顶点在△ABC 的边上.(保留作图痕迹)
②求所作的矩形的面积.
图 27. 3. 1 45
