27. 3. 2 位似(2)同步练习(无答案)2024-2025学年九年级下册数学人教版
文档属性
| 名称 | 27. 3. 2 位似(2)同步练习(无答案)2024-2025学年九年级下册数学人教版 | 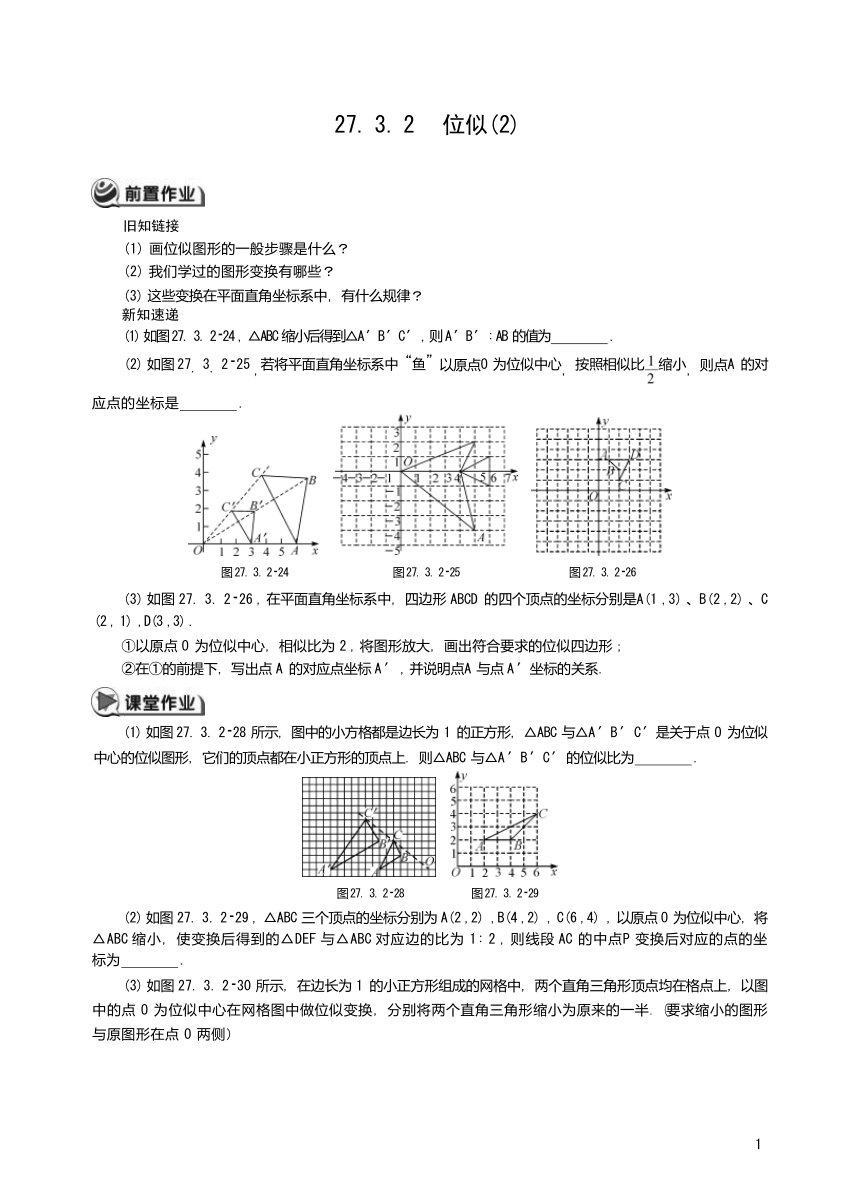 | |
| 格式 | docx | ||
| 文件大小 | 121.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 18:05:27 | ||
图片预览

文档简介
27. 3. 2 位似(2)
旧知链接
(1) 画位似图形的一般步骤是什么?
(2) 我们学过的图形变换有哪些?
(3) 这些变换在平面直角坐标系中,有什么规律? 新知速递
(1) 如图 27. 3. 2 24 , △ABC 缩小后得到△A ′B ′C ′ , 则 A ′B ′ ∶ AB 的值为 .
(2) 如图 27. 3. 2 25 ,若将平面直角坐标系中“鱼”以原点O 为位似中心,按照相似比缩小,则点A 的对
应点的坐标是 .
图 27. 3. 2 24 图 27. 3. 2 25 图 27. 3. 2 26
(3) 如图 27. 3. 2 26 , 在平面直角坐标系中,四边形 ABCD 的四个顶点的坐标分别是A(1 ,3) 、B(2 ,2) 、C (2 , 1) ,D(3 ,3) .
①以原点 O 为位似中心,相似比为 2 , 将图形放大,画出符合要求的位似四边形;
②在①的前提下,写出点 A 的对应点坐标 A ′ , 并说明点A 与点 A ′坐标的关系.
(1) 如图 27. 3. 2 28 所示,图中的小方格都是边长为 1 的正方形,△ABC 与△A ′B ′ C ′是关于点 O 为位似 中心的位似图形,它们的顶点都在小正方形的顶点上.则△ABC 与△A ′B ′C ′ 的位似比为 .
图 27. 3. 2 28 图 27. 3. 2 29
(2) 如图 27. 3. 2 29 , △ABC 三个顶点的坐标分别为 A(2 ,2) ,B(4 ,2) , C(6 ,4) , 以原点 O 为位似中心,将 △ABC 缩小,使变换后得到的△DEF 与△ABC 对应边的比为 1∶ 2 , 则线段 AC 的中点P 变换后对应的点的坐 标为 .
(3) 如图 27. 3. 2 30 所示,在边长为 1 的小正方形组成的网格中,两个直角三角形顶点均在格点上,以图 中的点 O 为位似中心在网格图中做位似变换,分别将两个直角三角形缩小为原来的一半.(要求缩小的图形 与原图形在点 O 两侧)
1
图 27. 3. 2 30 图 27. 3. 2 31
(4) 如图 27. 3. 2 31 所示,在对△AOB 依次进行位似、轴对称和平移变换后得到△A ′O ′B ′ , 在坐标纸上画 出这几次变换相应的图形.
基础训练
(1) 已知△ABC 在第一象限,则它关于原点位似的△A ′B ′C ′在( ) .
A. 第三象限 B. 第二象限
C. 第一象限 D. 第一或第三象限
(2) 如图 27. 3. 2 34 , 大鱼和小鱼是以 O 为位似中心位似图形,则小鱼上的点( a , b ) 对应大鱼上的 点( ) .
A. ( - a , - 2b) B. ( - 2a , - b) C. ( - 2a , - 2b) D. ( - 2b , - 2a)
图 27. 3. 2 34 图 27. 3. 2 35
(3) 如图 27. 3. 2 35 , 在平面直角坐标系中有△ABC , 以 O 点为位似中心,相似比为 2 , 将△ABC 放大,则 它的对应顶点的坐标是( ) .
A. (8 ,6) (6 ,2) (2 ,4)
B. ( - 8 , - 6) ( - 6 , - 2) ( - 2 , - 4)
C. (8 , - 6) (6 , - 2) (2 , - 4) 或( - 8 ,6) ( - 6 ,2) ( - 2 ,4)
D. (8 ,6) (6 ,2) (2 ,4) 或( - 8 , - 6) ( - 6 , - 2) ( - 2 , - 4)
(4) △ABC 和△A ′B ′C ′关于原点位似,且点 A( - 3 ,4) , 它的对应点 A ′ (6 , - 8) , 则△ABC 与△A ′B ′ C ′ 的 相似比是 .
(5) 在直角坐标系中,△ABC 的坐标分别是 A( - 1 ,2) , B( - 2 ,0) , C( - 1 , 1) , 若以原点 O 为位似中心, 将△ABC 放大到原来的 2 倍得到△A ′B ′C ′ , 那么落在第四象限的 A ′ 的坐标是 .
拓展提高
(1) 如图 27. 3. 2 36 , 在平面直角坐标系中有两点A(6 , 2) , B(6 ,0) , 以原点为位似中心,相似比为 1 ∶ 2. 则线段 AB 的对应线段 A ′B ′ 的长为 .
(2) 如图 27. 3. 2 37 , 原点 O 是△ABC 和△A ′B ′ C ′ 的位似中心,点 A (1 , 0 ) 与点 A ′ ( - 2 , 0 ) 是对应点,
△ABC 的面积是 ,则△A ′B ′C ′ 的面积是 .
2
图 27. 3. 2 36 图 27. 3. 2 37
(3) 如图 27. 3. 2 38 , 在边长均为 1 的小正方形网格纸中,△OAB 的顶点 O、A、B 均在格点上,且 O 是直 角坐标系的原点,点 A 在 x 轴上.
①以 O 为 位 似 中 心,将 △OAB 放 大,使 得 放 大 后 的 △OA 1 B 1 与 △OAB 对 应 线 段 的 比 为2∶ 1 , 画 出 △OA 1 B 1 ;
②在①的条件下,若线段 AB 上的一点P 的坐标为( a , b) ,请写出放大后,P 点的对应点 P 1 的坐标.
图 27. 3. 2 38
发散思维
(1) 在图 27. 3. 2 39 的方格纸中,△OAB 的顶点坐标分别为 O(0 ,0) 、A ( - 2 , - 1) 、B( - 1 , - 3 ) , △O 1 A 1 B 1 与△OAB 是关于点 P 为位似中心的位
(
图
27.
3.
2
39
)似图形. ①在图中标出位似中心 P 的位置,并写出点P 及点 B 的对应点 B 1 的坐标. ②以原点 O 为位似中心,在位似中心的同侧画出△OAB 的一个位 似△OA 2 B2 , 使它与△OAB 的相似比为 2 ∶ 1. 并写出点 B 的对应点 B2 的坐 标;③△OAB 内部一点 M 的坐标为( a , b) , 写出 M 在△OA 2 B2 中的对应点 M2 的坐标. ④判断△OA 2 B2 能否看作是由△O 1 A 1 B 1 经过某种变换后得到的 图形,若是,请指出是怎样变换得到的( 直接写答案).
(2) 如图 27. 3. 2 40 , 正方形网格中,小方格的边长为 1 厘米,小格的顶
点叫格点,△ABC 和△EFD 的三个顶点都在格点上,如果△EFD 是由△ABC 经过平移与位似两次几何变换 得到的.
①在图中画出第一次平移变换后的图形,并用图示法或文字表达两次几何变换的过程( 主要说明如何 变换).
②求△EFD 的外接圆的半径.
图 27. 3. 2 40
3
旧知链接
(1) 画位似图形的一般步骤是什么?
(2) 我们学过的图形变换有哪些?
(3) 这些变换在平面直角坐标系中,有什么规律? 新知速递
(1) 如图 27. 3. 2 24 , △ABC 缩小后得到△A ′B ′C ′ , 则 A ′B ′ ∶ AB 的值为 .
(2) 如图 27. 3. 2 25 ,若将平面直角坐标系中“鱼”以原点O 为位似中心,按照相似比缩小,则点A 的对
应点的坐标是 .
图 27. 3. 2 24 图 27. 3. 2 25 图 27. 3. 2 26
(3) 如图 27. 3. 2 26 , 在平面直角坐标系中,四边形 ABCD 的四个顶点的坐标分别是A(1 ,3) 、B(2 ,2) 、C (2 , 1) ,D(3 ,3) .
①以原点 O 为位似中心,相似比为 2 , 将图形放大,画出符合要求的位似四边形;
②在①的前提下,写出点 A 的对应点坐标 A ′ , 并说明点A 与点 A ′坐标的关系.
(1) 如图 27. 3. 2 28 所示,图中的小方格都是边长为 1 的正方形,△ABC 与△A ′B ′ C ′是关于点 O 为位似 中心的位似图形,它们的顶点都在小正方形的顶点上.则△ABC 与△A ′B ′C ′ 的位似比为 .
图 27. 3. 2 28 图 27. 3. 2 29
(2) 如图 27. 3. 2 29 , △ABC 三个顶点的坐标分别为 A(2 ,2) ,B(4 ,2) , C(6 ,4) , 以原点 O 为位似中心,将 △ABC 缩小,使变换后得到的△DEF 与△ABC 对应边的比为 1∶ 2 , 则线段 AC 的中点P 变换后对应的点的坐 标为 .
(3) 如图 27. 3. 2 30 所示,在边长为 1 的小正方形组成的网格中,两个直角三角形顶点均在格点上,以图 中的点 O 为位似中心在网格图中做位似变换,分别将两个直角三角形缩小为原来的一半.(要求缩小的图形 与原图形在点 O 两侧)
1
图 27. 3. 2 30 图 27. 3. 2 31
(4) 如图 27. 3. 2 31 所示,在对△AOB 依次进行位似、轴对称和平移变换后得到△A ′O ′B ′ , 在坐标纸上画 出这几次变换相应的图形.
基础训练
(1) 已知△ABC 在第一象限,则它关于原点位似的△A ′B ′C ′在( ) .
A. 第三象限 B. 第二象限
C. 第一象限 D. 第一或第三象限
(2) 如图 27. 3. 2 34 , 大鱼和小鱼是以 O 为位似中心位似图形,则小鱼上的点( a , b ) 对应大鱼上的 点( ) .
A. ( - a , - 2b) B. ( - 2a , - b) C. ( - 2a , - 2b) D. ( - 2b , - 2a)
图 27. 3. 2 34 图 27. 3. 2 35
(3) 如图 27. 3. 2 35 , 在平面直角坐标系中有△ABC , 以 O 点为位似中心,相似比为 2 , 将△ABC 放大,则 它的对应顶点的坐标是( ) .
A. (8 ,6) (6 ,2) (2 ,4)
B. ( - 8 , - 6) ( - 6 , - 2) ( - 2 , - 4)
C. (8 , - 6) (6 , - 2) (2 , - 4) 或( - 8 ,6) ( - 6 ,2) ( - 2 ,4)
D. (8 ,6) (6 ,2) (2 ,4) 或( - 8 , - 6) ( - 6 , - 2) ( - 2 , - 4)
(4) △ABC 和△A ′B ′C ′关于原点位似,且点 A( - 3 ,4) , 它的对应点 A ′ (6 , - 8) , 则△ABC 与△A ′B ′ C ′ 的 相似比是 .
(5) 在直角坐标系中,△ABC 的坐标分别是 A( - 1 ,2) , B( - 2 ,0) , C( - 1 , 1) , 若以原点 O 为位似中心, 将△ABC 放大到原来的 2 倍得到△A ′B ′C ′ , 那么落在第四象限的 A ′ 的坐标是 .
拓展提高
(1) 如图 27. 3. 2 36 , 在平面直角坐标系中有两点A(6 , 2) , B(6 ,0) , 以原点为位似中心,相似比为 1 ∶ 2. 则线段 AB 的对应线段 A ′B ′ 的长为 .
(2) 如图 27. 3. 2 37 , 原点 O 是△ABC 和△A ′B ′ C ′ 的位似中心,点 A (1 , 0 ) 与点 A ′ ( - 2 , 0 ) 是对应点,
△ABC 的面积是 ,则△A ′B ′C ′ 的面积是 .
2
图 27. 3. 2 36 图 27. 3. 2 37
(3) 如图 27. 3. 2 38 , 在边长均为 1 的小正方形网格纸中,△OAB 的顶点 O、A、B 均在格点上,且 O 是直 角坐标系的原点,点 A 在 x 轴上.
①以 O 为 位 似 中 心,将 △OAB 放 大,使 得 放 大 后 的 △OA 1 B 1 与 △OAB 对 应 线 段 的 比 为2∶ 1 , 画 出 △OA 1 B 1 ;
②在①的条件下,若线段 AB 上的一点P 的坐标为( a , b) ,请写出放大后,P 点的对应点 P 1 的坐标.
图 27. 3. 2 38
发散思维
(1) 在图 27. 3. 2 39 的方格纸中,△OAB 的顶点坐标分别为 O(0 ,0) 、A ( - 2 , - 1) 、B( - 1 , - 3 ) , △O 1 A 1 B 1 与△OAB 是关于点 P 为位似中心的位
(
图
27.
3.
2
39
)似图形. ①在图中标出位似中心 P 的位置,并写出点P 及点 B 的对应点 B 1 的坐标. ②以原点 O 为位似中心,在位似中心的同侧画出△OAB 的一个位 似△OA 2 B2 , 使它与△OAB 的相似比为 2 ∶ 1. 并写出点 B 的对应点 B2 的坐 标;③△OAB 内部一点 M 的坐标为( a , b) , 写出 M 在△OA 2 B2 中的对应点 M2 的坐标. ④判断△OA 2 B2 能否看作是由△O 1 A 1 B 1 经过某种变换后得到的 图形,若是,请指出是怎样变换得到的( 直接写答案).
(2) 如图 27. 3. 2 40 , 正方形网格中,小方格的边长为 1 厘米,小格的顶
点叫格点,△ABC 和△EFD 的三个顶点都在格点上,如果△EFD 是由△ABC 经过平移与位似两次几何变换 得到的.
①在图中画出第一次平移变换后的图形,并用图示法或文字表达两次几何变换的过程( 主要说明如何 变换).
②求△EFD 的外接圆的半径.
图 27. 3. 2 40
3
