28. 1. 3 锐角三角函数(3)同步练习(无答案)2024-2025学年九年级下册数学人教版
文档属性
| 名称 | 28. 1. 3 锐角三角函数(3)同步练习(无答案)2024-2025学年九年级下册数学人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 86.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 00:00:00 | ||
图片预览

文档简介
28. 1. 3 锐角三角函数(3)
旧知链接
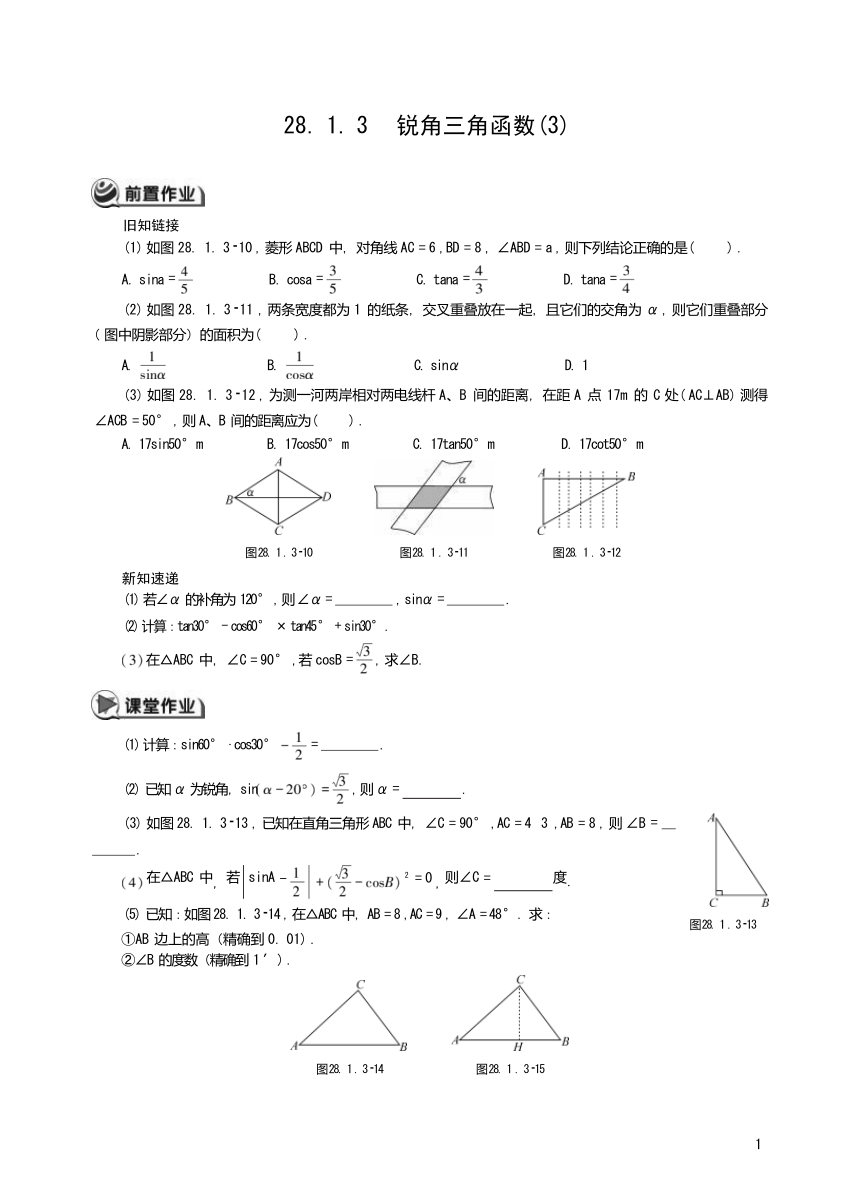
(1) 如图 28. 1. 3 10 , 菱形 ABCD 中,对角线 AC = 6 ,BD = 8 , ∠ABD = a , 则下列结论正确的是( ) .
A. sina = B. cosa = C. tana = D. tana =
(2) 如图 28. 1. 3 11 , 两条宽度都为 1 的纸条,交叉重叠放在一起,且它们的交角为 α , 则它们重叠部分 ( 图中阴影部分)的面积为( ) .
A. B. C. sinα D. 1
(3) 如图 28. 1. 3 12 , 为测一河两岸相对两电线杆 A、B 间的距离,在距 A 点 17m 的 C 处( AC⊥AB) 测得 ∠ACB = 50 ° , 则 A、B 间的距离应为( ) .
A. 17sin50 ° m B. 17cos50 ° m C. 17tan50 ° m D. 17cot50 ° m
图 28. 1 . 3 10 图 28. 1 . 3 11 图 28. 1 . 3 12
新知速递
(1) 若∠α 的补角为 120 ° , 则 ∠α = , sinα = .
(2) 计算:tan30 ° - cos60 ° × tan45 ° + sin30 ° .
在△ABC 中,∠C = 90 ° ,若 cosB = , 求∠B.
1
(1) 计算:sin60 ° ·cos30 ° = .
(2) 已知 α 为锐角,sin , 则 α = .
(3) 如图 28. 1. 3 13 , 已知在直角三角形 ABC 中,∠C = 90 ° ,AC = 4 3 ,AB = 8 , 则 ∠B =
.
在△ABC 中,若 sinA - 2 = 0 , 则∠C = 度.
(5) 已知:如图 28. 1. 3 14 , 在△ABC 中,AB = 8 ,AC = 9 , ∠A = 48 ° . 求:
①AB 边上的高(精确到 0. 01) .
②∠B 的度数(精确到 1 ′ ) .
图 28. 1 . 3 13
图 28. 1 . 3 14 图 28. 1 . 3 15
基础训练
(1) sin30°的相反数为( ) .
A. B. D.
(2) ∠A 是锐角,且 sinA = cosA , 则∠A 的度数是( ) .
A. 30 ° B. 45 ° C. 60 ° D. 75 °
(3) 若一个三角形三个内角度数的比为 1∶ 2∶ 3 , 那么这个三角形最小内角的正切值为( ) .
A. B. C. D.
已知 tan 则锐角 α 的度数是( ) .
A. 60 ° B. 45 ° C. 50 ° D. 75 °
(5) 计算 sin30 ° + cos60°所得结果为 .
(6) 如图 28. 1. 3 16 所示:将三角板的直角顶点放置在直线 AB 的点 O 处,使 斜边 CD∥AB , 则 ∠α 的正弦值是 .
(7) 已知 α 是锐角,tanα = 2cos30 ° , 那么 α = 度.
(
图
28. 1
.
3
16
) △ABC 中,若 | sinA - 2 = 0 , 则∠C = 度.
拓展提高
(1) 计算:①( sin245 ° - cos230 ° + sin230 ° ) ( tan45 ° - tan230 ° ) .
②2sin260 ° - 3 tan30 ° - 2cos245 ° .
(2) 如图 28. 1. 3 17 所示,在△ABC 中,∠A = 30 ° , ∠B = 45 ° ,AC = 2 3 , 求 AB 的长.
图 28. 1 . 3 17
发散思维
(1) 如图 28. 1. 3 18 所示,A、B 两城市相距 100 km , 现计划在这两座城市间修建一条高速公路( 即线段 AB) , 经测量,森林保护中心 P 在 A 城市的北偏东 30°和 B 城市的北偏西 45°的方向上,已知森林保护区的范 围在以 P 点为圆心,50 km 为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?
(参考数据: 3 ≈ 1. 732 , 2 ≈ 1. 414) .
图 28. 1 . 3 18
(2) 同学们,在我们进入高中以后,将还会学到下面三角函数公式:
sin( α - β) = sinαcosβ - cosαsinβ ;
cos( α - β) = cosαcosβ + sinαsinβ.
①试仿照例题,求出 cos15°的准确值;
②我们知道,tanα = 试求出 tan15°的准确值.
2
旧知链接
(1) 如图 28. 1. 3 10 , 菱形 ABCD 中,对角线 AC = 6 ,BD = 8 , ∠ABD = a , 则下列结论正确的是( ) .
A. sina = B. cosa = C. tana = D. tana =
(2) 如图 28. 1. 3 11 , 两条宽度都为 1 的纸条,交叉重叠放在一起,且它们的交角为 α , 则它们重叠部分 ( 图中阴影部分)的面积为( ) .
A. B. C. sinα D. 1
(3) 如图 28. 1. 3 12 , 为测一河两岸相对两电线杆 A、B 间的距离,在距 A 点 17m 的 C 处( AC⊥AB) 测得 ∠ACB = 50 ° , 则 A、B 间的距离应为( ) .
A. 17sin50 ° m B. 17cos50 ° m C. 17tan50 ° m D. 17cot50 ° m
图 28. 1 . 3 10 图 28. 1 . 3 11 图 28. 1 . 3 12
新知速递
(1) 若∠α 的补角为 120 ° , 则 ∠α = , sinα = .
(2) 计算:tan30 ° - cos60 ° × tan45 ° + sin30 ° .
在△ABC 中,∠C = 90 ° ,若 cosB = , 求∠B.
1
(1) 计算:sin60 ° ·cos30 ° = .
(2) 已知 α 为锐角,sin , 则 α = .
(3) 如图 28. 1. 3 13 , 已知在直角三角形 ABC 中,∠C = 90 ° ,AC = 4 3 ,AB = 8 , 则 ∠B =
.
在△ABC 中,若 sinA - 2 = 0 , 则∠C = 度.
(5) 已知:如图 28. 1. 3 14 , 在△ABC 中,AB = 8 ,AC = 9 , ∠A = 48 ° . 求:
①AB 边上的高(精确到 0. 01) .
②∠B 的度数(精确到 1 ′ ) .
图 28. 1 . 3 13
图 28. 1 . 3 14 图 28. 1 . 3 15
基础训练
(1) sin30°的相反数为( ) .
A. B. D.
(2) ∠A 是锐角,且 sinA = cosA , 则∠A 的度数是( ) .
A. 30 ° B. 45 ° C. 60 ° D. 75 °
(3) 若一个三角形三个内角度数的比为 1∶ 2∶ 3 , 那么这个三角形最小内角的正切值为( ) .
A. B. C. D.
已知 tan 则锐角 α 的度数是( ) .
A. 60 ° B. 45 ° C. 50 ° D. 75 °
(5) 计算 sin30 ° + cos60°所得结果为 .
(6) 如图 28. 1. 3 16 所示:将三角板的直角顶点放置在直线 AB 的点 O 处,使 斜边 CD∥AB , 则 ∠α 的正弦值是 .
(7) 已知 α 是锐角,tanα = 2cos30 ° , 那么 α = 度.
(
图
28. 1
.
3
16
) △ABC 中,若 | sinA - 2 = 0 , 则∠C = 度.
拓展提高
(1) 计算:①( sin245 ° - cos230 ° + sin230 ° ) ( tan45 ° - tan230 ° ) .
②2sin260 ° - 3 tan30 ° - 2cos245 ° .
(2) 如图 28. 1. 3 17 所示,在△ABC 中,∠A = 30 ° , ∠B = 45 ° ,AC = 2 3 , 求 AB 的长.
图 28. 1 . 3 17
发散思维
(1) 如图 28. 1. 3 18 所示,A、B 两城市相距 100 km , 现计划在这两座城市间修建一条高速公路( 即线段 AB) , 经测量,森林保护中心 P 在 A 城市的北偏东 30°和 B 城市的北偏西 45°的方向上,已知森林保护区的范 围在以 P 点为圆心,50 km 为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?
(参考数据: 3 ≈ 1. 732 , 2 ≈ 1. 414) .
图 28. 1 . 3 18
(2) 同学们,在我们进入高中以后,将还会学到下面三角函数公式:
sin( α - β) = sinαcosβ - cosαsinβ ;
cos( α - β) = cosαcosβ + sinαsinβ.
①试仿照例题,求出 cos15°的准确值;
②我们知道,tanα = 试求出 tan15°的准确值.
2
